Classical test theory approach to detecting unidirectional and bidirectional (with one crossing location) DIF. This family of statistics is intended for unidimensional tests, and applies a regression-corrected matched-total score approach to quantify the response bias between two or more groups. Can be used for DIF, DBF, and DTF testing with two or more discrete groups.
Usage
SIBTEST(
dat,
group,
suspect_set,
match_set,
focal_name = unique(group)[2],
guess_correction = 0,
Jmin = 5,
na.rm = FALSE,
randomize = FALSE,
C = cbind(1, -diag(length(unique(group)) - 1L)),
pairwise = FALSE,
DIF = FALSE,
p.adjust.method = "none",
permute = 1000,
pk_focal = FALSE,
correction = TRUE,
remove_cross = FALSE,
details = FALSE,
plot = "none",
...
)Arguments
- dat
integer-based dataset to be tested, containing dichotomous or polytomous responses
- group
a (factor) vector indicating group membership with the same length as the number of rows in
dat- suspect_set
an integer vector indicating which items to inspect with SIBTEST. Including only one value will perform a DIF test, while including more than one will perform a simultaneous bundle test (DBF); including all non-matched items will perform DTF. If missing, a simultaneous test using all the items not listed in match_set will be used (i.e., DTF)
- match_set
an integer vector indicating which items to use as the items which are matched (i.e., contain no DIF). These are analogous to 'anchor' items in the likelihood method to locate DIF. If missing, all items other than the items found in the
suspect_setwill be used- focal_name
name of the focal group; e.g.,
'focal'. If not specified then one will be selected automatically usingunique(group)[2]- guess_correction
a vector of numbers from 0 to 1 indicating how much to correct the items for guessing. It's length should be the same as ncol(dat)
- Jmin
the minimum number of observations required when splitting the data into focal and reference groups conditioned on the matched set
- na.rm
logical; remove rows in
datwith any missing values? IfTRUE, rows with missing data will be removed, as well as the corresponding elements in thegroupinput- randomize
logical; perform the crossing test for non-compensatory bias using Li and Stout's (1996) permutation approach? Default is
FALSE, which uses the ad-hoc mixed degrees of freedom method suggested by Chalmers (2018)- C
a contrast matrix to use for pooled testing with more than two groups. Default uses an effects coding approach, where the last group (last column of the matrix) is treated as the reference group, and each column is associated with the respective name via
unique(group)(i.e., the first column is the coefficient forunique(group)[1], second column forunique(group)[2], and so on)- pairwise
logical; perform pairwise comparisons in multi-group applications?
- DIF
logical; should the elements in
suspect_setbe treated one at a time to test for DIF? Use of this logical will treat all other items as part of thematch_setunless this input is provided explicitly. Default isFALSEto allow DBF and DTF tests- p.adjust.method
a character input dictating which
methodto use inp.adjust. when studying more than two groups. Default does not present any p-value adjustments- permute
number of permutations to perform when
randomize = TRUE. Default is 1000- pk_focal
logical; using the group weights from the focal group instead of the total sample? Default is FALSE as per Shealy and Stout's recommendation
- correction
logical; apply the composite correction for the difference between focal composite scores using the true-score regression technique? Default is
TRUE, reflecting Shealy and Stout's linear extrapolation method- remove_cross
logical; remove the subtest information associated with the approximate crossing location? If TRUE this reflects the CSIBTEST definition of Li and Stout (1996); if FALSE, this reflects the version of CSIBTEST utilized by Chalmers (2018). Only applicable in two-group settings (in multi-group this is fixed to FALSE)
- details
logical; return a data.frame containing the details required to compute SIBTEST?
- plot
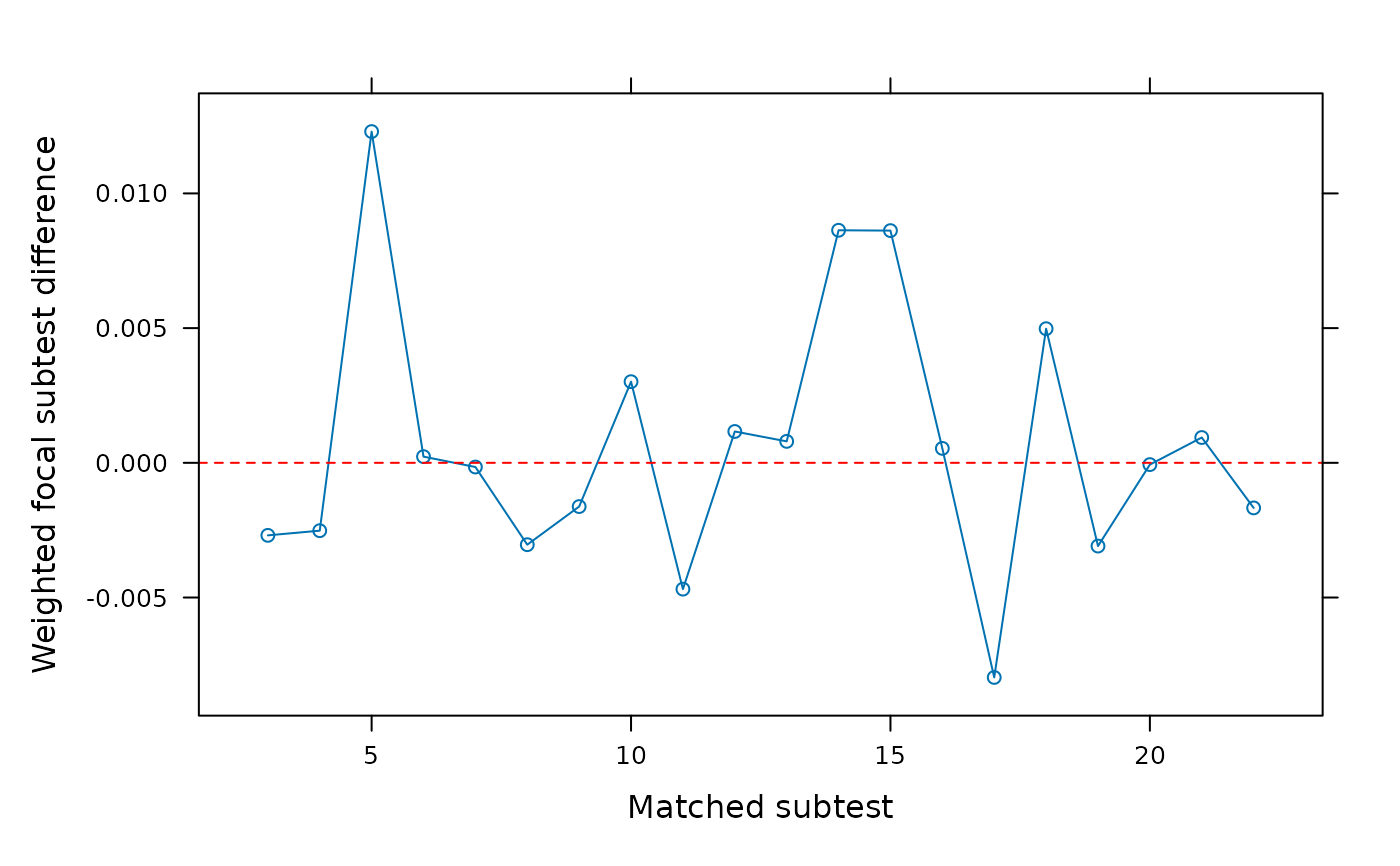
a character input indicating the type of plot to construct. Options are
'none'(default),'observed'for the scaled focal subtest scores against the matched subtest scores,'weights'for the proportion weights used (i.e., the proportion of observations at each matched score),'difference'for the difference between the scaled focal subtest scores against the matched subtest scores, and'wdifference'for the conditional differences multiplied by each respective weight. Note that the last plot reflects the components used in SIBTEST, and therefore the sum of these plotted observations will equal the beta coefficient for SIBTEST- ...
additional plotting arguments to be passed
Details
SIBTEST is similar to the Mantel-Haenszel approach for detecting DIF but uses a regression correction based on the KR-20/coefficient alpha reliability index to correct the observed differences when the latent trait distributions are not equal. Function supports the standard SIBTEST for dichotomous and polytomous data (compensatory) and supports crossing DIF testing (i.e., non-compensatory/non-uniform) using the asymptotic sampling distribution version of the Crossing-SIBTEST (CSIBTEST) statistic described by Chalmers (2018) and the permutation method described by Li and Stout (1996). This function also supports the multi-group generalizations (GSIBTEST and GCSIBTEST) proposed by Chalmers and Zheng (2023), where users may specify alternative contrast matrices to evaluate specific comparisons between groups as well as perform joint hypothesis tests.
References
Chalmers, R. P. (2018). Improving the Crossing-SIBTEST statistic for detecting non-uniform DIF. Psychometrika, 83, 2, 376-386.
Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06
Chalmers, R. P. & Zheng, G. (2023). Multi-group Generalizations of SIBTEST and Crossing-SIBTEST. Applied Measurement in Education, 36(2), 171-191, doi:10.1080/08957347.2023.2201703 .
Chang, H. H., Mazzeo, J. & Roussos, L. (1996). DIF for Polytomously Scored Items: An Adaptation of the SIBTEST Procedure. Journal of Educational Measurement, 33, 333-353.
Li, H.-H. & Stout, W. (1996). A new procedure for detection of crossing DIF. Psychometrika, 61, 647-677.
Shealy, R. & Stout, W. (1993). A model-based standardization approach that separates true bias/DIF from group ability differences and detect test bias/DTF as well as item bias/DIF. Psychometrika, 58, 159-194.
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
if (FALSE) { # \dontrun{
set.seed(1234)
n <- 30
N <- 500
a <- matrix(1, n)
d <- matrix(rnorm(n), n)
group <- c(rep('reference', N), rep('focal', N*2))
## -------------
# groups completely equal
dat1 <- simdata(a, d, N, itemtype = 'dich')
dat2 <- simdata(a, d, N*2, itemtype = 'dich')
dat <- rbind(dat1, dat2)
# DIF (all other items as anchors)
SIBTEST(dat, group, suspect_set = 6)
# Some plots depicting the above tests
SIBTEST(dat, group, suspect_set = 6, plot = 'observed')
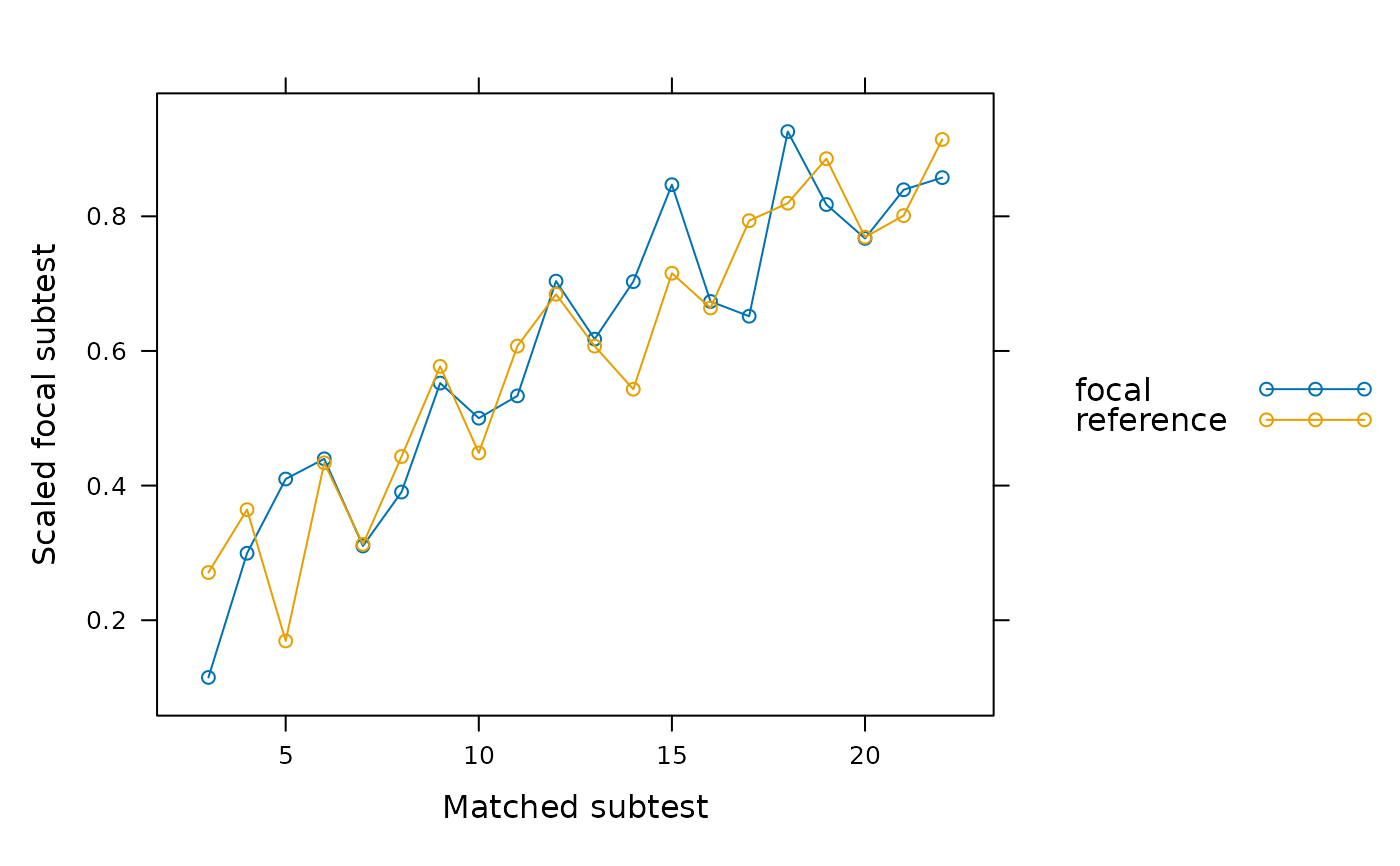SIBTEST(dat, group, suspect_set = 6, plot = 'weights')
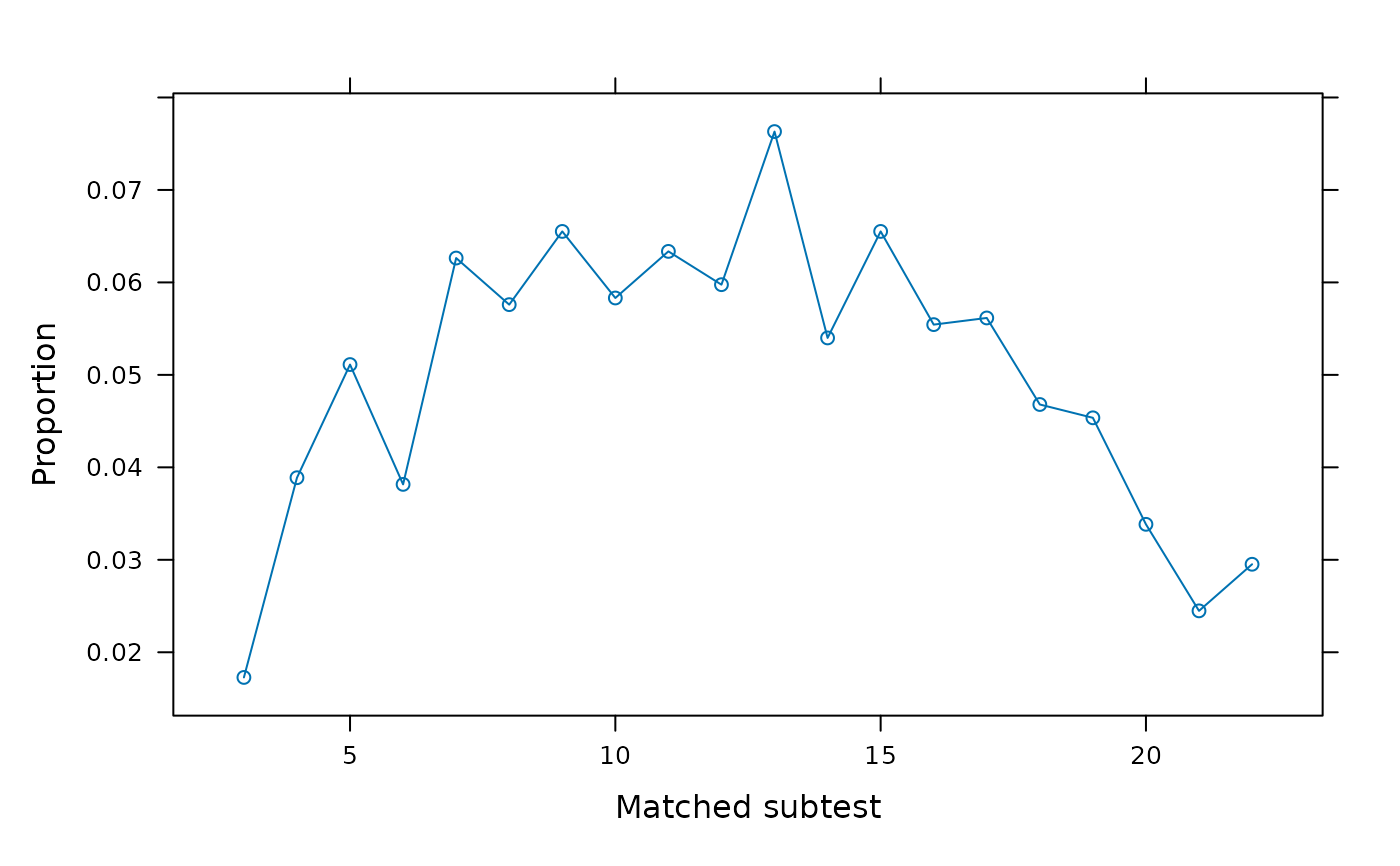SIBTEST(dat, group, suspect_set = 6, plot = 'wdifference')
# Include CSIBTEST with randomization method
SIBTEST(dat, group, suspect_set = 6, randomize = TRUE)
# remove crossing-location (identical to Li and Stout 1996 definition of CSIBTEST)
SIBTEST(dat, group, suspect_set = 6, randomize = TRUE, remove_cross=TRUE)
# DIF (specific anchors)
SIBTEST(dat, group, match_set = 1:5, suspect_set = 6)
SIBTEST(dat, group, match_set = 1:5, suspect_set = 6, randomize=TRUE)
# DBF (all and specific anchors, respectively)
SIBTEST(dat, group, suspect_set = 11:30)
SIBTEST(dat, group, match_set = 1:5, suspect_set = 11:30)
# DTF
SIBTEST(dat, group, suspect_set = 11:30)
SIBTEST(dat, group, match_set = 1:10) #equivalent
# different hyper pars
dat1 <- simdata(a, d, N, itemtype = 'dich')
dat2 <- simdata(a, d, N*2, itemtype = 'dich', mu = .5, sigma = matrix(1.5))
dat <- rbind(dat1, dat2)
SIBTEST(dat, group, 6:30)
SIBTEST(dat, group, 11:30)
# DIF testing with anchors 1 through 5
SIBTEST(dat, group, 6, match_set = 1:5)
SIBTEST(dat, group, 7, match_set = 1:5)
SIBTEST(dat, group, 8, match_set = 1:5)
# DIF testing with all other items as anchors
SIBTEST(dat, group, 6)
SIBTEST(dat, group, 7)
SIBTEST(dat, group, 8)
## -------------
## systematic differing slopes and intercepts (clear DTF)
dat1 <- simdata(a, d, N, itemtype = 'dich')
dat2 <- simdata(a + c(numeric(15), rnorm(n-15, 1, .25)), d + c(numeric(15), rnorm(n-15, 1, 1)),
N*2, itemtype = 'dich')
dat <- rbind(dat1, dat2)
SIBTEST(dat, group, 6:30)
SIBTEST(dat, group, 11:30)
# Some plots depicting the above tests
SIBTEST(dat, group, suspect_set = 11:30, plot = 'observed')
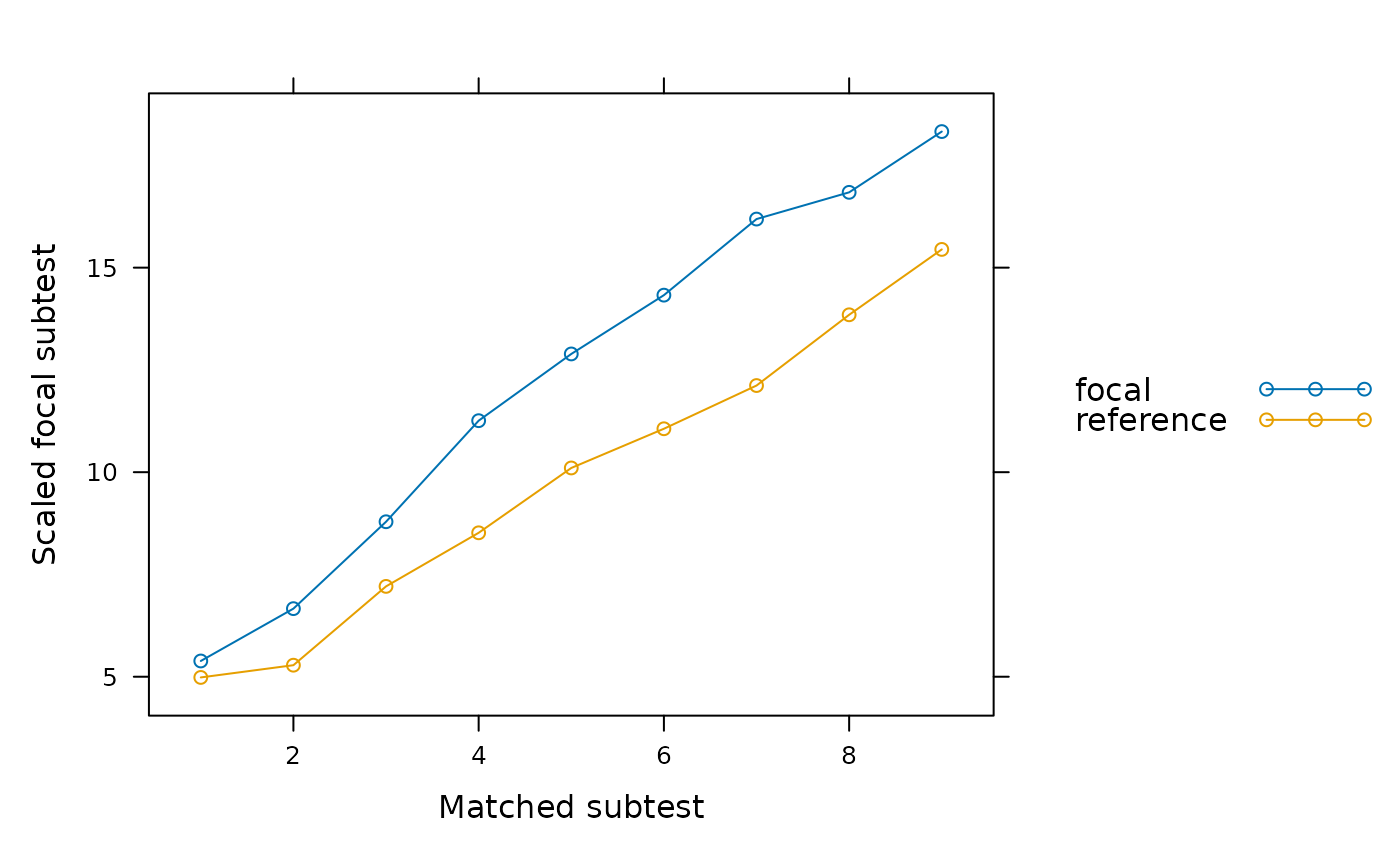SIBTEST(dat, group, suspect_set = 11:30, plot = 'weights')
SIBTEST(dat, group, suspect_set = 11:30, plot = 'wdifference')
# DIF testing using valid anchors
SIBTEST(dat, group, suspect_set = 6, match_set = 1:5)
SIBTEST(dat, group, suspect_set = 7, match_set = 1:5)
SIBTEST(dat, group, suspect_set = 30, match_set = 1:5)
# test DIF using specific match_set
SIBTEST(dat, group, suspect_set = 6:30, match_set = 1:5, DIF=TRUE)
# test DIF using all-other-as-anchors method (not typically recommended)
SIBTEST(dat, group, suspect_set = 1:30, DIF=TRUE)
# randomization method is fairly poor when smaller matched-set used
SIBTEST(dat, group, suspect_set = 30, match_set = 1:5, randomize=TRUE)
SIBTEST(dat, group, suspect_set = 30, randomize=TRUE)
## ----------------------------------
# three group SIBTEST test
set.seed(1234)
n <- 30
N <- 1000
a <- matrix(1, n)
d <- matrix(rnorm(n), n)
group <- c(rep('group1', N), rep('group2', N), rep('group3', N))
# groups completely equal
dat1 <- simdata(a, d, N, itemtype = 'dich')
dat2 <- simdata(a, d, N, itemtype = 'dich')
dat3 <- simdata(a, d, N, itemtype = 'dich')
dat <- rbind(dat1, dat2, dat3)
# omnibus test using effects-coding contrast matrix (default)
SIBTEST(dat, group, suspect_set = 6)
SIBTEST(dat, group, suspect_set = 6, randomize=TRUE)
# explicit contrasts
SIBTEST(dat, group, suspect_set = 6, randomize=TRUE,
C = matrix(c(1,-1,0), 1))
# test all items for DIF
SIBTEST(dat, group, suspect_set = 1:ncol(dat), DIF=TRUE)
SIBTEST(dat, group, suspect_set = 16:ncol(dat), DIF=TRUE,
match_set = 1:15) # specific anchors
# post-hoc between two groups only
pick <- group %in% c('group1', 'group2')
SIBTEST(subset(dat, pick), group[pick], suspect_set = 1:ncol(dat), DIF=TRUE)
# post-hoc pairwise comparison for all groups
SIBTEST(dat, group, suspect_set = 1:ncol(dat), DIF=TRUE, pairwise = TRUE)
## systematic differing slopes and intercepts
dat2 <- simdata(a + c(numeric(15), .5,.5,.5,.5,.5, numeric(10)),
d + c(numeric(15), 0,.6,.7,.8,.9, numeric(10)),
N, itemtype = 'dich')
dat <- rbind(dat1, dat2, dat3)
SIBTEST(dat, group, suspect_set = 16)
SIBTEST(dat, group, suspect_set = 16, randomize=TRUE)
SIBTEST(dat, group, suspect_set = 19)
SIBTEST(dat, group, suspect_set = 19, randomize=TRUE)
SIBTEST(dat, group, suspect_set = c(16, 19), DIF=TRUE)
SIBTEST(dat, group, suspect_set = c(16, 19), DIF=TRUE, pairwise=TRUE)
} # }