Given an internal mirt item object extracted by using extract.item,
compute the item information.
Arguments
- x
an extracted internal mirt object containing item information (see
extract.item)- Theta
a vector (unidimensional) or matrix (multidimensional) of latent trait values
- degrees
a vector of angles in degrees that are between 0 and 90. Only applicable when the input object is multidimensional
- total.info
logical; return the total information curve for the item? If
FALSE, information curves for each category are returned as a matrix- multidim_matrix
logical; compute the information matrix for each row in
Theta? IfThetacontains more than 1 row then a list of matrices will be returned, otherwise ifThetahas exactly one row then a matrix will be returned
References
Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
mod <- mirt(Science, 1)
extr.2 <- extract.item(mod, 2)
Theta <- matrix(seq(-4,4, by = .1))
info.2 <- iteminfo(extr.2, Theta)
#do something with the info?
plot(Theta, info.2, type = 'l', main = 'Item information')
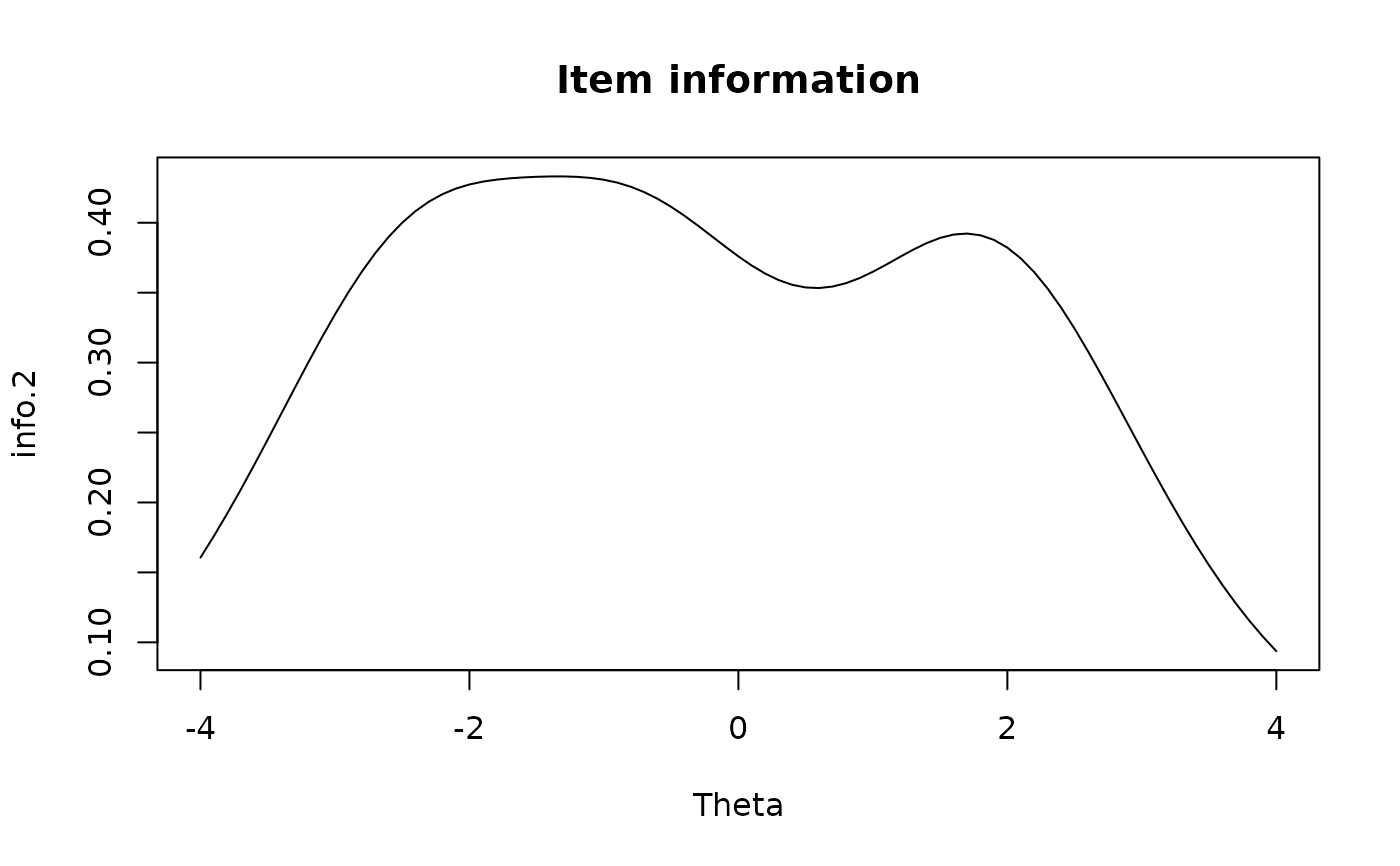 # \donttest{
#category information curves
cat.info <- iteminfo(extr.2, Theta, total.info = FALSE)
plot(Theta, cat.info[,1], type = 'l', ylim = c(0, max(cat.info)),
ylab = 'info', main = 'Category information')
for(i in 2:ncol(cat.info))
lines(Theta, cat.info[,i], col = i)
# \donttest{
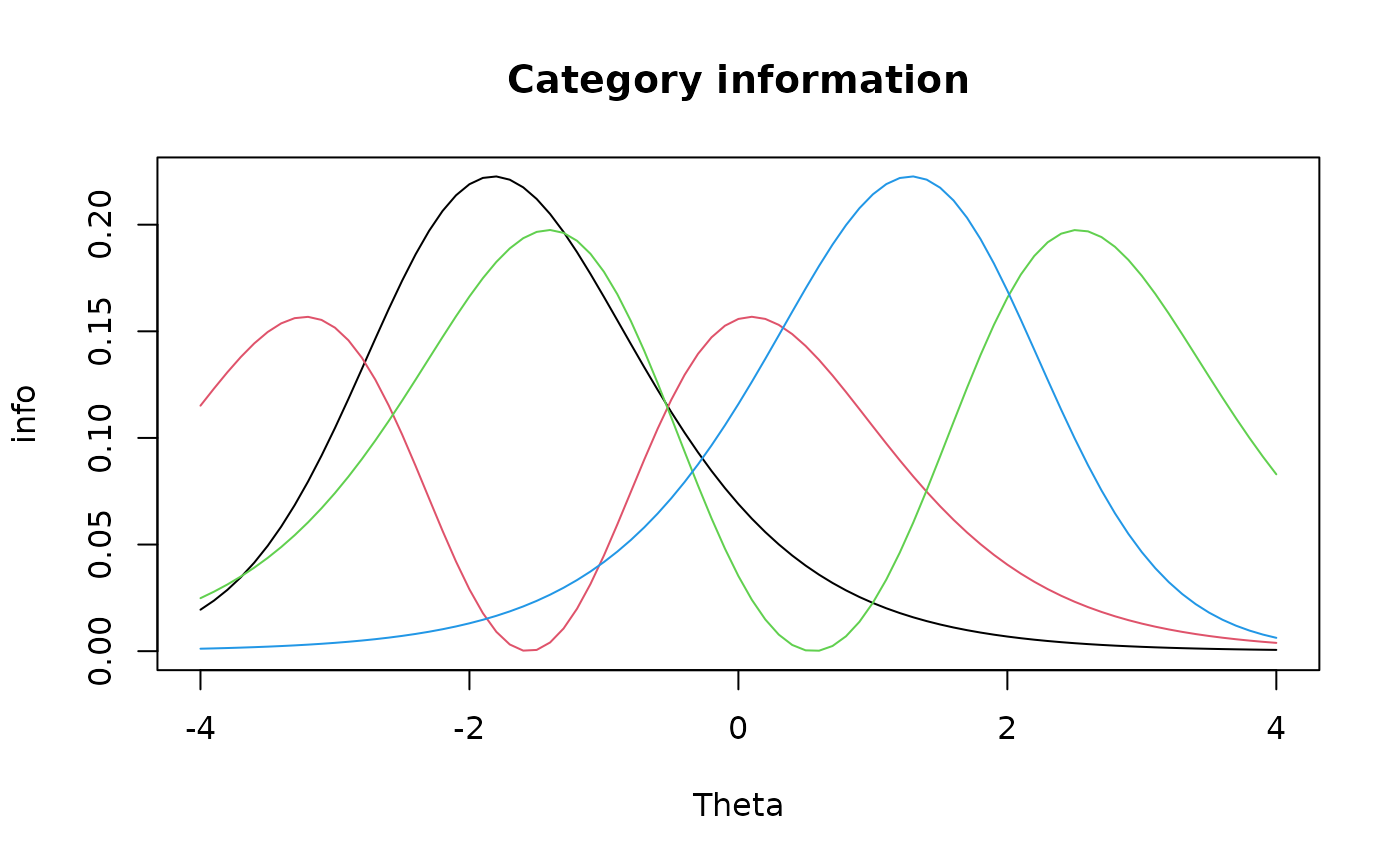
#category information curves
cat.info <- iteminfo(extr.2, Theta, total.info = FALSE)
plot(Theta, cat.info[,1], type = 'l', ylim = c(0, max(cat.info)),
ylab = 'info', main = 'Category information')
for(i in 2:ncol(cat.info))
lines(Theta, cat.info[,i], col = i)
 ## Customized test information plot
T1 <- T2 <- 0
dat <- expand.table(LSAT7)
mod1 <- mirt(dat, 1)
mod2 <- mirt(dat, 1, 'Rasch')
for(i in 1:5){
T1 <- T1 + iteminfo(extract.item(mod1, i), Theta)
T2 <- T2 + iteminfo(extract.item(mod2, i), Theta)
}
plot(Theta, T2/T1, type = 'l', ylab = 'Relative Test Information', las = 1)
lines(Theta, T1/T1, col = 'red')
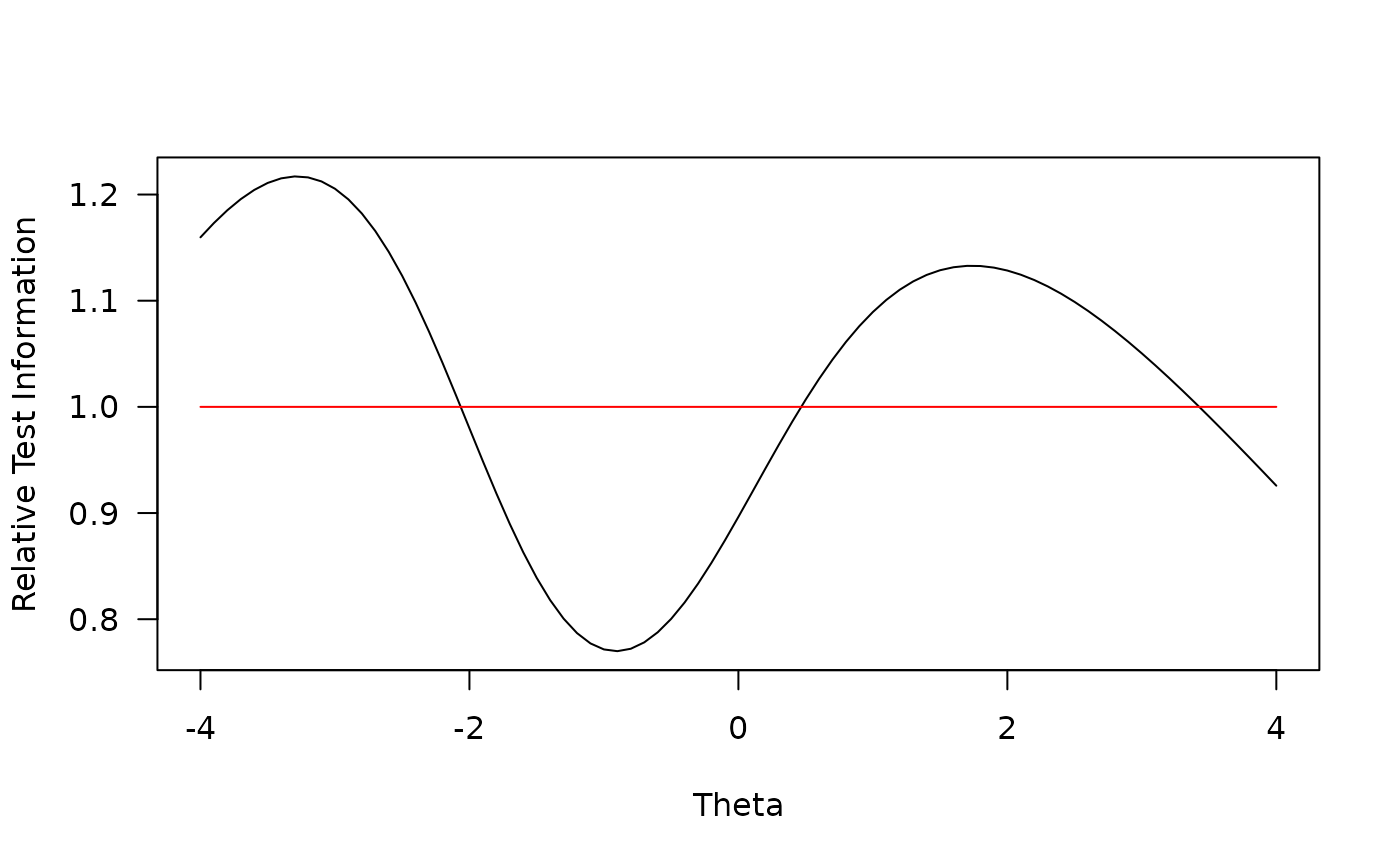
## Customized test information plot
T1 <- T2 <- 0
dat <- expand.table(LSAT7)
mod1 <- mirt(dat, 1)
mod2 <- mirt(dat, 1, 'Rasch')
for(i in 1:5){
T1 <- T1 + iteminfo(extract.item(mod1, i), Theta)
T2 <- T2 + iteminfo(extract.item(mod2, i), Theta)
}
plot(Theta, T2/T1, type = 'l', ylab = 'Relative Test Information', las = 1)
lines(Theta, T1/T1, col = 'red')
 # multidimensional
mod <- mirt(dat, 2, TOL=1e-2)
ii <- extract.item(mod, 1)
Theta <- as.matrix(expand.grid(-4:4, -4:4))
iteminfo(ii, Theta, degrees=c(45,45)) # equal angle
#> [1] 9.135853e-04 3.804627e-03 1.534609e-02 5.457783e-02 1.280846e-01
#> [6] 1.263872e-01 5.292862e-02 1.479382e-02 3.661942e-03 6.367175e-04
#> [11] 2.659764e-03 1.086462e-02 4.056306e-02 1.103087e-01 1.394001e-01
#> [16] 6.967460e-02 2.076774e-02 5.230188e-03 4.436266e-04 1.857138e-03
#> [21] 7.653659e-03 2.959372e-02 9.036811e-02 1.443711e-01 8.885547e-02
#> [26] 2.887817e-02 7.452148e-03 3.090296e-04 1.295613e-03 5.372790e-03
#> [31] 2.130057e-02 7.105538e-02 1.400859e-01 1.088343e-01 3.962912e-02
#> [36] 1.058186e-02 2.152390e-04 9.033338e-04 3.762362e-03 1.518269e-02
#> [41] 5.409208e-02 1.275949e-01 1.268897e-01 5.340700e-02 1.495328e-02
#> [46] 1.498990e-04 6.295660e-04 2.630098e-03 1.074696e-02 4.017519e-02
#> [51] 1.097011e-01 1.396891e-01 7.024317e-02 2.098631e-02 1.043871e-04
#> [56] 4.386406e-04 1.836367e-03 7.569796e-03 2.929632e-02 8.974279e-02
#> [61] 1.443776e-01 8.947966e-02 2.917186e-02 7.268993e-05 3.055547e-04
#> [66] 1.281094e-03 5.313435e-03 2.107900e-02 7.048336e-02 1.398084e-01
#> [71] 1.094447e-01 4.001273e-02 5.061591e-05 2.128179e-04 8.931970e-04
#> [76] 3.720561e-03 1.502092e-02 5.360938e-02 1.270998e-01 1.273870e-01
#> [81] 5.388842e-02
iteminfo(ii, Theta, degrees=c(90,0)) # first dimension only
#> [1] 2.073184e-04 8.633775e-04 3.482462e-03 1.238525e-02 2.906603e-02
#> [6] 2.868083e-02 1.201100e-02 3.357135e-03 8.309983e-04 1.444892e-04
#> [11] 6.035756e-04 2.465490e-03 9.204906e-03 2.503218e-02 3.163384e-02
#> [16] 1.581114e-02 4.712787e-03 1.186878e-03 1.006714e-04 4.214372e-04
#> [21] 1.736832e-03 6.715652e-03 2.050708e-02 3.276188e-02 2.016382e-02
#> [26] 6.553273e-03 1.691103e-03 7.012756e-05 2.940112e-04 1.219238e-03
#> [31] 4.833701e-03 1.612448e-02 3.178946e-02 2.469758e-02 8.992970e-03
#> [36] 2.401323e-03 4.884381e-05 2.049920e-04 8.537865e-04 3.445381e-03
#> [41] 1.227502e-02 2.895489e-02 2.879486e-02 1.211956e-02 3.393322e-03
#> [46] 3.401633e-05 1.428663e-04 5.968437e-04 2.438790e-03 9.116887e-03
#> [51] 2.489429e-02 3.169942e-02 1.594016e-02 4.762389e-03 2.368839e-05
#> [56] 9.953996e-05 4.167236e-04 1.717801e-03 6.648164e-03 2.036518e-02
#> [61] 3.276337e-02 2.030547e-02 6.619919e-03 1.649540e-05 6.933901e-05
#> [66] 2.907165e-04 1.205769e-03 4.783421e-03 1.599467e-02 3.172649e-02
#> [71] 2.483609e-02 9.080022e-03 1.148618e-05 4.829441e-05 2.026917e-04
#> [76] 8.443006e-04 3.408672e-03 1.216548e-02 2.884253e-02 2.890771e-02
#> [81] 1.222881e-02
# information matrices
iteminfo(ii, Theta, multidim_matrix = TRUE)
#> [[1]]
#> [,1] [,2]
#> [1,] 0.0032654333 -0.0008227905
#> [2,] -0.0008227905 0.0002073184
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 0.013598901 -0.0034265121
#> [2,] -0.003426512 0.0008633775
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 0.05485162 -0.013820952
#> [2,] -0.01382095 0.003482462
#>
#> [[4]]
#> [,1] [,2]
#> [1,] 0.19507785 -0.04915373
#> [2,] -0.04915373 0.01238525
#>
#> [[5]]
#> [,1] [,2]
#> [1,] 0.4578137 -0.11535522
#> [2,] -0.1153552 0.02906603
#>
#> [[6]]
#> [,1] [,2]
#> [1,] 0.4517464 -0.11382645
#> [2,] -0.1138265 0.02868083
#>
#> [[7]]
#> [,1] [,2]
#> [1,] 0.18918306 -0.04766842
#> [2,] -0.04766842 0.01201100
#>
#> [[8]]
#> [,1] [,2]
#> [1,] 0.05287762 -0.013323563
#> [2,] -0.01332356 0.003357135
#>
#> [[9]]
#> [,1] [,2]
#> [1,] 0.013088902 -0.0032980078
#> [2,] -0.003298008 0.0008309983
#>
#> [[10]]
#> [,1] [,2]
#> [1,] 0.0022758231 -0.0005734387
#> [2,] -0.0005734387 0.0001444892
#>
#> [[11]]
#> [,1] [,2]
#> [1,] 0.009506809 -0.0023954286
#> [2,] -0.002395429 0.0006035756
#>
#> [[12]]
#> [,1] [,2]
#> [1,] 0.038833480 -0.009784864
#> [2,] -0.009784864 0.002465490
#>
#> [[13]]
#> [,1] [,2]
#> [1,] 0.14498478 -0.036531784
#> [2,] -0.03653178 0.009204906
#>
#> [[14]]
#> [,1] [,2]
#> [1,] 0.39427721 -0.09934594
#> [2,] -0.09934594 0.02503218
#>
#> [[15]]
#> [,1] [,2]
#> [1,] 0.4982588 -0.12554615
#> [2,] -0.1255462 0.03163384
#>
#> [[16]]
#> [,1] [,2]
#> [1,] 0.24903832 -0.06275013
#> [2,] -0.06275013 0.01581114
#>
#> [[17]]
#> [,1] [,2]
#> [1,] 0.07423024 -0.018703779
#> [2,] -0.01870378 0.004712787
#>
#> [[18]]
#> [,1] [,2]
#> [1,] 0.018694291 -0.004710397
#> [2,] -0.004710397 0.001186878
#>
#> [[19]]
#> [,1] [,2]
#> [1,] 0.0015856573 -0.0003995377
#> [2,] -0.0003995377 0.0001006714
#>
#> [[20]]
#> [,1] [,2]
#> [1,] 0.006637979 -0.0016725702
#> [2,] -0.001672570 0.0004214372
#>
#> [[21]]
#> [,1] [,2]
#> [1,] 0.027356520 -0.006893016
#> [2,] -0.006893016 0.001736832
#>
#> [[22]]
#> [,1] [,2]
#> [1,] 0.10577700 -0.026652608
#> [2,] -0.02665261 0.006715652
#>
#> [[23]]
#> [,1] [,2]
#> [1,] 0.32300327 -0.08138706
#> [2,] -0.08138706 0.02050708
#>
#> [[24]]
#> [,1] [,2]
#> [1,] 0.5160263 -0.13002305
#> [2,] -0.1300230 0.03276188
#>
#> [[25]]
#> [,1] [,2]
#> [1,] 0.31759663 -0.08002475
#> [2,] -0.08002475 0.02016382
#>
#> [[26]]
#> [,1] [,2]
#> [1,] 0.10321940 -0.026008170
#> [2,] -0.02600817 0.006553273
#>
#> [[27]]
#> [,1] [,2]
#> [1,] 0.026636258 -0.006711532
#> [2,] -0.006711532 0.001691103
#>
#> [[28]]
#> [,1] [,2]
#> [1,] 0.0011045662 -2.783173e-04
#> [2,] -0.0002783173 7.012756e-05
#>
#> [[29]]
#> [,1] [,2]
#> [1,] 0.004630917 -0.0011668512
#> [2,] -0.001166851 0.0002940112
#>
#> [[30]]
#> [,1] [,2]
#> [1,] 0.019203995 -0.004838826
#> [2,] -0.004838826 0.001219238
#>
#> [[31]]
#> [,1] [,2]
#> [1,] 0.07613474 -0.019183655
#> [2,] -0.01918365 0.004833701
#>
#> [[32]]
#> [,1] [,2]
#> [1,] 0.25397366 -0.06399369
#> [2,] -0.06399369 0.01612448
#>
#> [[33]]
#> [,1] [,2]
#> [1,] 0.5007100 -0.12616378
#> [2,] -0.1261638 0.03178946
#>
#> [[34]]
#> [,1] [,2]
#> [1,] 0.38900703 -0.09801802
#> [2,] -0.09801802 0.02469758
#>
#> [[35]]
#> [,1] [,2]
#> [1,] 0.14164661 -0.03569067
#> [2,] -0.03569067 0.00899297
#>
#> [[36]]
#> [,1] [,2]
#> [1,] 0.037822803 -0.009530204
#> [2,] -0.009530204 0.002401323
#>
#> [[37]]
#> [,1] [,2]
#> [1,] 0.0007693299 -1.938479e-04
#> [2,] -0.0001938479 4.884381e-05
#>
#> [[38]]
#> [,1] [,2]
#> [1,] 0.0032287914 -0.0008135579
#> [2,] -0.0008135579 0.0002049920
#>
#> [[39]]
#> [,1] [,2]
#> [1,] 0.013447834 -0.0033884478
#> [2,] -0.003388448 0.0008537865
#>
#> [[40]]
#> [,1] [,2]
#> [1,] 0.05426756 -0.013673786
#> [2,] -0.01367379 0.003445381
#>
#> [[41]]
#> [,1] [,2]
#> [1,] 0.19334166 -0.04871626
#> [2,] -0.04871626 0.01227502
#>
#> [[42]]
#> [,1] [,2]
#> [1,] 0.4560631 -0.11491412
#> [2,] -0.1149141 0.02895489
#>
#> [[43]]
#> [,1] [,2]
#> [1,] 0.4535425 -0.11427901
#> [2,] -0.1142790 0.02879486
#>
#> [[44]]
#> [,1] [,2]
#> [1,] 0.19089294 -0.04809925
#> [2,] -0.04809925 0.01211956
#>
#> [[45]]
#> [,1] [,2]
#> [1,] 0.05344759 -0.013467177
#> [2,] -0.01346718 0.003393322
#>
#> [[46]]
#> [,1] [,2]
#> [1,] 0.0005357850 -1.350016e-04
#> [2,] -0.0001350016 3.401633e-05
#>
#> [[47]]
#> [,1] [,2]
#> [1,] 0.0022502615 -0.0005669979
#> [2,] -0.0005669979 0.0001428663
#>
#> [[48]]
#> [,1] [,2]
#> [1,] 0.009400776 -0.0023687115
#> [2,] -0.002368711 0.0005968437
#>
#> [[49]]
#> [,1] [,2]
#> [1,] 0.03841294 -0.00967890
#> [2,] -0.00967890 0.00243879
#>
#> [[50]]
#> [,1] [,2]
#> [1,] 0.14359841 -0.036182461
#> [2,] -0.03618246 0.009116887
#>
#> [[51]]
#> [,1] [,2]
#> [1,] 0.39210544 -0.09879872
#> [2,] -0.09879872 0.02489429
#>
#> [[52]]
#> [,1] [,2]
#> [1,] 0.4992917 -0.12580642
#> [2,] -0.1258064 0.03169942
#>
#> [[53]]
#> [,1] [,2]
#> [1,] 0.2510706 -0.06326220
#> [2,] -0.0632622 0.01594016
#>
#> [[54]]
#> [,1] [,2]
#> [1,] 0.07501151 -0.018900633
#> [2,] -0.01890063 0.004762389
#>
#> [[55]]
#> [,1] [,2]
#> [1,] 3.731115e-04 -9.401283e-05
#> [2,] -9.401283e-05 2.368839e-05
#>
#> [[56]]
#> [,1] [,2]
#> [1,] 0.0015678356 -3.950472e-04
#> [2,] -0.0003950472 9.953996e-05
#>
#> [[57]]
#> [,1] [,2]
#> [1,] 0.006563736 -0.0016538632
#> [2,] -0.001653863 0.0004167236
#>
#> [[58]]
#> [,1] [,2]
#> [1,] 0.027056766 -0.006817487
#> [2,] -0.006817487 0.001717801
#>
#> [[59]]
#> [,1] [,2]
#> [1,] 0.10471401 -0.026384768
#> [2,] -0.02638477 0.006648164
#>
#> [[60]]
#> [,1] [,2]
#> [1,] 0.32076818 -0.08082389
#> [2,] -0.08082389 0.02036518
#>
#> [[61]]
#> [,1] [,2]
#> [1,] 0.5160498 -0.13002897
#> [2,] -0.1300290 0.03276337
#>
#> [[62]]
#> [,1] [,2]
#> [1,] 0.31982769 -0.08058691
#> [2,] -0.08058691 0.02030547
#>
#> [[63]]
#> [,1] [,2]
#> [1,] 0.10426913 -0.026272671
#> [2,] -0.02627267 0.006619919
#>
#> [[64]]
#> [,1] [,2]
#> [1,] 2.598160e-04 -6.546579e-05
#> [2,] -6.546579e-05 1.649540e-05
#>
#> [[65]]
#> [,1] [,2]
#> [1,] 0.0010921460 -2.751878e-04
#> [2,] -0.0002751878 6.933901e-05
#>
#> [[66]]
#> [,1] [,2]
#> [1,] 0.004579021 -0.0011537750
#> [2,] -0.001153775 0.0002907165
#>
#> [[67]]
#> [,1] [,2]
#> [1,] 0.01899184 -0.004785370
#> [2,] -0.00478537 0.001205769
#>
#> [[68]]
#> [,1] [,2]
#> [1,] 0.07534278 -0.018984105
#> [2,] -0.01898410 0.004783421
#>
#> [[69]]
#> [,1] [,2]
#> [1,] 0.25192908 -0.06347852
#> [2,] -0.06347852 0.01599467
#>
#> [[70]]
#> [,1] [,2]
#> [1,] 0.4997181 -0.12591387
#> [2,] -0.1259139 0.03172649
#>
#> [[71]]
#> [,1] [,2]
#> [1,] 0.39118867 -0.09856773
#> [2,] -0.09856773 0.02483609
#>
#> [[72]]
#> [,1] [,2]
#> [1,] 0.14301775 -0.036036152
#> [2,] -0.03603615 0.009080022
#>
#> [[73]]
#> [,1] [,2]
#> [1,] 1.809167e-04 -4.558555e-05
#> [2,] -4.558555e-05 1.148618e-05
#>
#> [[74]]
#> [,1] [,2]
#> [1,] 0.0007606764 -1.916675e-04
#> [2,] -0.0001916675 4.829441e-05
#>
#> [[75]]
#> [,1] [,2]
#> [1,] 0.0031925594 -0.0008044285
#> [2,] -0.0008044285 0.0002026917
#>
#> [[76]]
#> [,1] [,2]
#> [1,] 0.013298423 -0.0033508008
#> [2,] -0.003350801 0.0008443006
#>
#> [[77]]
#> [,1] [,2]
#> [1,] 0.05368936 -0.013528096
#> [2,] -0.01352810 0.003408672
#>
#> [[78]]
#> [,1] [,2]
#> [1,] 0.19161632 -0.04828152
#> [2,] -0.04828152 0.01216548
#>
#> [[79]]
#> [,1] [,2]
#> [1,] 0.4542934 -0.11446821
#> [2,] -0.1144682 0.02884253
#>
#> [[80]]
#> [,1] [,2]
#> [1,] 0.4553201 -0.11472690
#> [2,] -0.1147269 0.02890771
#>
#> [[81]]
#> [,1] [,2]
#> [1,] 0.19261370 -0.04853283
#> [2,] -0.04853283 0.01222881
#>
iteminfo(ii, Theta[1, , drop=FALSE], multidim_matrix = TRUE)
#> [,1] [,2]
#> [1,] 0.0032654333 -0.0008227905
#> [2,] -0.0008227905 0.0002073184
# }
# multidimensional
mod <- mirt(dat, 2, TOL=1e-2)
ii <- extract.item(mod, 1)
Theta <- as.matrix(expand.grid(-4:4, -4:4))
iteminfo(ii, Theta, degrees=c(45,45)) # equal angle
#> [1] 9.135853e-04 3.804627e-03 1.534609e-02 5.457783e-02 1.280846e-01
#> [6] 1.263872e-01 5.292862e-02 1.479382e-02 3.661942e-03 6.367175e-04
#> [11] 2.659764e-03 1.086462e-02 4.056306e-02 1.103087e-01 1.394001e-01
#> [16] 6.967460e-02 2.076774e-02 5.230188e-03 4.436266e-04 1.857138e-03
#> [21] 7.653659e-03 2.959372e-02 9.036811e-02 1.443711e-01 8.885547e-02
#> [26] 2.887817e-02 7.452148e-03 3.090296e-04 1.295613e-03 5.372790e-03
#> [31] 2.130057e-02 7.105538e-02 1.400859e-01 1.088343e-01 3.962912e-02
#> [36] 1.058186e-02 2.152390e-04 9.033338e-04 3.762362e-03 1.518269e-02
#> [41] 5.409208e-02 1.275949e-01 1.268897e-01 5.340700e-02 1.495328e-02
#> [46] 1.498990e-04 6.295660e-04 2.630098e-03 1.074696e-02 4.017519e-02
#> [51] 1.097011e-01 1.396891e-01 7.024317e-02 2.098631e-02 1.043871e-04
#> [56] 4.386406e-04 1.836367e-03 7.569796e-03 2.929632e-02 8.974279e-02
#> [61] 1.443776e-01 8.947966e-02 2.917186e-02 7.268993e-05 3.055547e-04
#> [66] 1.281094e-03 5.313435e-03 2.107900e-02 7.048336e-02 1.398084e-01
#> [71] 1.094447e-01 4.001273e-02 5.061591e-05 2.128179e-04 8.931970e-04
#> [76] 3.720561e-03 1.502092e-02 5.360938e-02 1.270998e-01 1.273870e-01
#> [81] 5.388842e-02
iteminfo(ii, Theta, degrees=c(90,0)) # first dimension only
#> [1] 2.073184e-04 8.633775e-04 3.482462e-03 1.238525e-02 2.906603e-02
#> [6] 2.868083e-02 1.201100e-02 3.357135e-03 8.309983e-04 1.444892e-04
#> [11] 6.035756e-04 2.465490e-03 9.204906e-03 2.503218e-02 3.163384e-02
#> [16] 1.581114e-02 4.712787e-03 1.186878e-03 1.006714e-04 4.214372e-04
#> [21] 1.736832e-03 6.715652e-03 2.050708e-02 3.276188e-02 2.016382e-02
#> [26] 6.553273e-03 1.691103e-03 7.012756e-05 2.940112e-04 1.219238e-03
#> [31] 4.833701e-03 1.612448e-02 3.178946e-02 2.469758e-02 8.992970e-03
#> [36] 2.401323e-03 4.884381e-05 2.049920e-04 8.537865e-04 3.445381e-03
#> [41] 1.227502e-02 2.895489e-02 2.879486e-02 1.211956e-02 3.393322e-03
#> [46] 3.401633e-05 1.428663e-04 5.968437e-04 2.438790e-03 9.116887e-03
#> [51] 2.489429e-02 3.169942e-02 1.594016e-02 4.762389e-03 2.368839e-05
#> [56] 9.953996e-05 4.167236e-04 1.717801e-03 6.648164e-03 2.036518e-02
#> [61] 3.276337e-02 2.030547e-02 6.619919e-03 1.649540e-05 6.933901e-05
#> [66] 2.907165e-04 1.205769e-03 4.783421e-03 1.599467e-02 3.172649e-02
#> [71] 2.483609e-02 9.080022e-03 1.148618e-05 4.829441e-05 2.026917e-04
#> [76] 8.443006e-04 3.408672e-03 1.216548e-02 2.884253e-02 2.890771e-02
#> [81] 1.222881e-02
# information matrices
iteminfo(ii, Theta, multidim_matrix = TRUE)
#> [[1]]
#> [,1] [,2]
#> [1,] 0.0032654333 -0.0008227905
#> [2,] -0.0008227905 0.0002073184
#>
#> [[2]]
#> [,1] [,2]
#> [1,] 0.013598901 -0.0034265121
#> [2,] -0.003426512 0.0008633775
#>
#> [[3]]
#> [,1] [,2]
#> [1,] 0.05485162 -0.013820952
#> [2,] -0.01382095 0.003482462
#>
#> [[4]]
#> [,1] [,2]
#> [1,] 0.19507785 -0.04915373
#> [2,] -0.04915373 0.01238525
#>
#> [[5]]
#> [,1] [,2]
#> [1,] 0.4578137 -0.11535522
#> [2,] -0.1153552 0.02906603
#>
#> [[6]]
#> [,1] [,2]
#> [1,] 0.4517464 -0.11382645
#> [2,] -0.1138265 0.02868083
#>
#> [[7]]
#> [,1] [,2]
#> [1,] 0.18918306 -0.04766842
#> [2,] -0.04766842 0.01201100
#>
#> [[8]]
#> [,1] [,2]
#> [1,] 0.05287762 -0.013323563
#> [2,] -0.01332356 0.003357135
#>
#> [[9]]
#> [,1] [,2]
#> [1,] 0.013088902 -0.0032980078
#> [2,] -0.003298008 0.0008309983
#>
#> [[10]]
#> [,1] [,2]
#> [1,] 0.0022758231 -0.0005734387
#> [2,] -0.0005734387 0.0001444892
#>
#> [[11]]
#> [,1] [,2]
#> [1,] 0.009506809 -0.0023954286
#> [2,] -0.002395429 0.0006035756
#>
#> [[12]]
#> [,1] [,2]
#> [1,] 0.038833480 -0.009784864
#> [2,] -0.009784864 0.002465490
#>
#> [[13]]
#> [,1] [,2]
#> [1,] 0.14498478 -0.036531784
#> [2,] -0.03653178 0.009204906
#>
#> [[14]]
#> [,1] [,2]
#> [1,] 0.39427721 -0.09934594
#> [2,] -0.09934594 0.02503218
#>
#> [[15]]
#> [,1] [,2]
#> [1,] 0.4982588 -0.12554615
#> [2,] -0.1255462 0.03163384
#>
#> [[16]]
#> [,1] [,2]
#> [1,] 0.24903832 -0.06275013
#> [2,] -0.06275013 0.01581114
#>
#> [[17]]
#> [,1] [,2]
#> [1,] 0.07423024 -0.018703779
#> [2,] -0.01870378 0.004712787
#>
#> [[18]]
#> [,1] [,2]
#> [1,] 0.018694291 -0.004710397
#> [2,] -0.004710397 0.001186878
#>
#> [[19]]
#> [,1] [,2]
#> [1,] 0.0015856573 -0.0003995377
#> [2,] -0.0003995377 0.0001006714
#>
#> [[20]]
#> [,1] [,2]
#> [1,] 0.006637979 -0.0016725702
#> [2,] -0.001672570 0.0004214372
#>
#> [[21]]
#> [,1] [,2]
#> [1,] 0.027356520 -0.006893016
#> [2,] -0.006893016 0.001736832
#>
#> [[22]]
#> [,1] [,2]
#> [1,] 0.10577700 -0.026652608
#> [2,] -0.02665261 0.006715652
#>
#> [[23]]
#> [,1] [,2]
#> [1,] 0.32300327 -0.08138706
#> [2,] -0.08138706 0.02050708
#>
#> [[24]]
#> [,1] [,2]
#> [1,] 0.5160263 -0.13002305
#> [2,] -0.1300230 0.03276188
#>
#> [[25]]
#> [,1] [,2]
#> [1,] 0.31759663 -0.08002475
#> [2,] -0.08002475 0.02016382
#>
#> [[26]]
#> [,1] [,2]
#> [1,] 0.10321940 -0.026008170
#> [2,] -0.02600817 0.006553273
#>
#> [[27]]
#> [,1] [,2]
#> [1,] 0.026636258 -0.006711532
#> [2,] -0.006711532 0.001691103
#>
#> [[28]]
#> [,1] [,2]
#> [1,] 0.0011045662 -2.783173e-04
#> [2,] -0.0002783173 7.012756e-05
#>
#> [[29]]
#> [,1] [,2]
#> [1,] 0.004630917 -0.0011668512
#> [2,] -0.001166851 0.0002940112
#>
#> [[30]]
#> [,1] [,2]
#> [1,] 0.019203995 -0.004838826
#> [2,] -0.004838826 0.001219238
#>
#> [[31]]
#> [,1] [,2]
#> [1,] 0.07613474 -0.019183655
#> [2,] -0.01918365 0.004833701
#>
#> [[32]]
#> [,1] [,2]
#> [1,] 0.25397366 -0.06399369
#> [2,] -0.06399369 0.01612448
#>
#> [[33]]
#> [,1] [,2]
#> [1,] 0.5007100 -0.12616378
#> [2,] -0.1261638 0.03178946
#>
#> [[34]]
#> [,1] [,2]
#> [1,] 0.38900703 -0.09801802
#> [2,] -0.09801802 0.02469758
#>
#> [[35]]
#> [,1] [,2]
#> [1,] 0.14164661 -0.03569067
#> [2,] -0.03569067 0.00899297
#>
#> [[36]]
#> [,1] [,2]
#> [1,] 0.037822803 -0.009530204
#> [2,] -0.009530204 0.002401323
#>
#> [[37]]
#> [,1] [,2]
#> [1,] 0.0007693299 -1.938479e-04
#> [2,] -0.0001938479 4.884381e-05
#>
#> [[38]]
#> [,1] [,2]
#> [1,] 0.0032287914 -0.0008135579
#> [2,] -0.0008135579 0.0002049920
#>
#> [[39]]
#> [,1] [,2]
#> [1,] 0.013447834 -0.0033884478
#> [2,] -0.003388448 0.0008537865
#>
#> [[40]]
#> [,1] [,2]
#> [1,] 0.05426756 -0.013673786
#> [2,] -0.01367379 0.003445381
#>
#> [[41]]
#> [,1] [,2]
#> [1,] 0.19334166 -0.04871626
#> [2,] -0.04871626 0.01227502
#>
#> [[42]]
#> [,1] [,2]
#> [1,] 0.4560631 -0.11491412
#> [2,] -0.1149141 0.02895489
#>
#> [[43]]
#> [,1] [,2]
#> [1,] 0.4535425 -0.11427901
#> [2,] -0.1142790 0.02879486
#>
#> [[44]]
#> [,1] [,2]
#> [1,] 0.19089294 -0.04809925
#> [2,] -0.04809925 0.01211956
#>
#> [[45]]
#> [,1] [,2]
#> [1,] 0.05344759 -0.013467177
#> [2,] -0.01346718 0.003393322
#>
#> [[46]]
#> [,1] [,2]
#> [1,] 0.0005357850 -1.350016e-04
#> [2,] -0.0001350016 3.401633e-05
#>
#> [[47]]
#> [,1] [,2]
#> [1,] 0.0022502615 -0.0005669979
#> [2,] -0.0005669979 0.0001428663
#>
#> [[48]]
#> [,1] [,2]
#> [1,] 0.009400776 -0.0023687115
#> [2,] -0.002368711 0.0005968437
#>
#> [[49]]
#> [,1] [,2]
#> [1,] 0.03841294 -0.00967890
#> [2,] -0.00967890 0.00243879
#>
#> [[50]]
#> [,1] [,2]
#> [1,] 0.14359841 -0.036182461
#> [2,] -0.03618246 0.009116887
#>
#> [[51]]
#> [,1] [,2]
#> [1,] 0.39210544 -0.09879872
#> [2,] -0.09879872 0.02489429
#>
#> [[52]]
#> [,1] [,2]
#> [1,] 0.4992917 -0.12580642
#> [2,] -0.1258064 0.03169942
#>
#> [[53]]
#> [,1] [,2]
#> [1,] 0.2510706 -0.06326220
#> [2,] -0.0632622 0.01594016
#>
#> [[54]]
#> [,1] [,2]
#> [1,] 0.07501151 -0.018900633
#> [2,] -0.01890063 0.004762389
#>
#> [[55]]
#> [,1] [,2]
#> [1,] 3.731115e-04 -9.401283e-05
#> [2,] -9.401283e-05 2.368839e-05
#>
#> [[56]]
#> [,1] [,2]
#> [1,] 0.0015678356 -3.950472e-04
#> [2,] -0.0003950472 9.953996e-05
#>
#> [[57]]
#> [,1] [,2]
#> [1,] 0.006563736 -0.0016538632
#> [2,] -0.001653863 0.0004167236
#>
#> [[58]]
#> [,1] [,2]
#> [1,] 0.027056766 -0.006817487
#> [2,] -0.006817487 0.001717801
#>
#> [[59]]
#> [,1] [,2]
#> [1,] 0.10471401 -0.026384768
#> [2,] -0.02638477 0.006648164
#>
#> [[60]]
#> [,1] [,2]
#> [1,] 0.32076818 -0.08082389
#> [2,] -0.08082389 0.02036518
#>
#> [[61]]
#> [,1] [,2]
#> [1,] 0.5160498 -0.13002897
#> [2,] -0.1300290 0.03276337
#>
#> [[62]]
#> [,1] [,2]
#> [1,] 0.31982769 -0.08058691
#> [2,] -0.08058691 0.02030547
#>
#> [[63]]
#> [,1] [,2]
#> [1,] 0.10426913 -0.026272671
#> [2,] -0.02627267 0.006619919
#>
#> [[64]]
#> [,1] [,2]
#> [1,] 2.598160e-04 -6.546579e-05
#> [2,] -6.546579e-05 1.649540e-05
#>
#> [[65]]
#> [,1] [,2]
#> [1,] 0.0010921460 -2.751878e-04
#> [2,] -0.0002751878 6.933901e-05
#>
#> [[66]]
#> [,1] [,2]
#> [1,] 0.004579021 -0.0011537750
#> [2,] -0.001153775 0.0002907165
#>
#> [[67]]
#> [,1] [,2]
#> [1,] 0.01899184 -0.004785370
#> [2,] -0.00478537 0.001205769
#>
#> [[68]]
#> [,1] [,2]
#> [1,] 0.07534278 -0.018984105
#> [2,] -0.01898410 0.004783421
#>
#> [[69]]
#> [,1] [,2]
#> [1,] 0.25192908 -0.06347852
#> [2,] -0.06347852 0.01599467
#>
#> [[70]]
#> [,1] [,2]
#> [1,] 0.4997181 -0.12591387
#> [2,] -0.1259139 0.03172649
#>
#> [[71]]
#> [,1] [,2]
#> [1,] 0.39118867 -0.09856773
#> [2,] -0.09856773 0.02483609
#>
#> [[72]]
#> [,1] [,2]
#> [1,] 0.14301775 -0.036036152
#> [2,] -0.03603615 0.009080022
#>
#> [[73]]
#> [,1] [,2]
#> [1,] 1.809167e-04 -4.558555e-05
#> [2,] -4.558555e-05 1.148618e-05
#>
#> [[74]]
#> [,1] [,2]
#> [1,] 0.0007606764 -1.916675e-04
#> [2,] -0.0001916675 4.829441e-05
#>
#> [[75]]
#> [,1] [,2]
#> [1,] 0.0031925594 -0.0008044285
#> [2,] -0.0008044285 0.0002026917
#>
#> [[76]]
#> [,1] [,2]
#> [1,] 0.013298423 -0.0033508008
#> [2,] -0.003350801 0.0008443006
#>
#> [[77]]
#> [,1] [,2]
#> [1,] 0.05368936 -0.013528096
#> [2,] -0.01352810 0.003408672
#>
#> [[78]]
#> [,1] [,2]
#> [1,] 0.19161632 -0.04828152
#> [2,] -0.04828152 0.01216548
#>
#> [[79]]
#> [,1] [,2]
#> [1,] 0.4542934 -0.11446821
#> [2,] -0.1144682 0.02884253
#>
#> [[80]]
#> [,1] [,2]
#> [1,] 0.4553201 -0.11472690
#> [2,] -0.1147269 0.02890771
#>
#> [[81]]
#> [,1] [,2]
#> [1,] 0.19261370 -0.04853283
#> [2,] -0.04853283 0.01222881
#>
iteminfo(ii, Theta[1, , drop=FALSE], multidim_matrix = TRUE)
#> [,1] [,2]
#> [1,] 0.0032654333 -0.0008227905
#> [2,] -0.0008227905 0.0002073184
# }