Differential item functioning statistics

This function runs the Wald and likelihood-ratio approaches for testing differential item functioning (DIF) with two or more groups. This is primarily a convenience wrapper to the multipleGroup function for performing standard DIF procedures. Independent models can be estimated in parallel by defining a parallel object with mirtCluster, which will help to decrease the run time. For best results, the baseline model should contain a set of 'anchor' items and have freely estimated hyper-parameters in the focal groups.

Usage

DIF(
  MGmodel,
  which.par,
  scheme = "add",
  items2test = 1:extract.mirt(MGmodel, "nitems"),
  groups2test = "all",
  seq_stat = "SABIC",
  Wald = FALSE,
  p.adjust = "none",
  pairwise = FALSE,
  return_models = FALSE,
  return_seq_model = FALSE,
  max_run = Inf,
  plotdif = FALSE,
  type = "trace",
  simplify = TRUE,
  verbose = TRUE,
  ...
)

Arguments

MGmodel

an object returned from multipleGroup to be used as the reference model

which.par

a character vector containing the parameter names which will be inspected for DIF

scheme

type of DIF analysis to perform, either by adding or dropping constraints across groups. These can be:

'add'

parameters in which.par will be constrained each item one at a time for items that are specified in items2test. This is beneficial when examining DIF from a model with parameters freely estimated across groups, and when inspecting differences via the Wald test

'drop'

parameters in which.par will be freely estimated for items that are specified in items2test. This is useful when supplying an overly restrictive model and attempting to detect DIF with a slightly less restrictive model

'add_sequential'

sequentially loop over the items being tested, and at the end of the loop treat DIF tests that satisfy the seq_stat criteria as invariant. The loop is then re-run on the remaining invariant items to determine if they are now displaying DIF in the less constrained model, and when no new invariant item is found the algorithm stops and returns the items that displayed DIF. Note that the DIF statistics are relative to this final, less constrained model which includes the DIF effects

'drop_sequential'

sequentially loop over the items being tested, and at the end of the loop treat items that violate the seq_stat criteria as demonstrating DIF. The loop is then re-run, leaving the items that previously demonstrated DIF as variable across groups, and the remaining test items that previously showed invariance are re-tested. The algorithm stops when no more items showing DIF are found and returns the items that displayed DIF. Note that the DIF statistics are relative to this final, less constrained model which includes the DIF effects

items2test

a numeric vector, or character vector containing the item names, indicating which items will be tested for DIF. In models where anchor items are known, omit them from this vector. For example, if items 1 and 2 are anchors in a 10 item test, then items2test = 3:10 would work for testing the remaining items (important to remember when using sequential schemes)

groups2test

a character vector indicating which groups to use in the DIF testing investigations. Default is 'all', which uses all group information to perform joint hypothesis tests of DIF (for a two group setup these result in pair-wise tests). For example, if the group names were 'g1', 'g2' and 'g3', and DIF was only to be investigated between group 'g1' and 'g3' then pass groups2test = c('g1', 'g3')

seq_stat

select a statistic to test for in the sequential schemes. Potential values are (in descending order of power) 'AIC', 'SABIC', 'HQ', and 'BIC'. If a numeric value is input that ranges between 0 and 1, the 'p' value will be tested (e.g., seq_stat = .05 will test for the difference of p < .05 in the add scheme, or p > .05 in the drop scheme), along with the specified p.adjust input

Wald

logical; perform Wald tests for DIF instead of likelihood ratio test?

p.adjust

string to be passed to the p.adjust function to adjust p-values. Adjustments are located in the adj_p element in the returned list

pairwise

logical; perform pairwise tests between groups when the number of groups is greater than 2? Useful as quickly specified post-hoc tests

return_models

logical; return estimated model objects for further analysis? Default is FALSE

return_seq_model

logical; on the last iteration of the sequential schemes, return the fitted multiple-group model containing the freely estimated parameters indicative of DIF? This is generally only useful when scheme = 'add_sequential'. Default is FALSE

max_run

a number indicating the maximum number of cycles to perform in sequential searches. The default is to perform search until no further DIF is found

plotdif

logical; create item plots for items that are displaying DIF according to the seq_stat criteria? Only available for 'add' type schemes

type

the type of plot argument passed to plot(). Default is 'trace', though another good option is 'infotrace'. For ease of viewing, the facet_item argument to mirt's plot() function is set to TRUE

simplify

logical; simplify the output by returning a data.frame object with the differences between AIC, BIC, etc, as well as the chi-squared test (X2) and associated df and p-values

verbose

logical print extra information to the console?

...

additional arguments to be passed to multipleGroup and plot

Value

a mirt_df object with the information-based criteria for DIF, though this may be changed to a list output when return_models or simplify are modified. As well, a silent 'DIF_coefficeints' attribute is included to view the item parameter differences between the groups

Details

Generally, the pre-computed baseline model should have been configured with two estimation properties: 1) a set of 'anchor' items, where the anchor items have various parameters that have been constrained to be equal across the groups, and 2) contain freely estimated latent mean and variance terms in all but one group (the so-called 'reference' group). These two properties help to fix the metric of the groups so that item parameter estimates do not contain latent distribution characteristics.

References

Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06

Chalmers, R. P., Counsell, A., and Flora, D. B. (2016). It might not make a big DIF: Improved Differential Test Functioning statistics that account for sampling variability. Educational and Psychological Measurement, 76, 114-140. doi:10.1177/0013164415584576

See also

multipleGroup, DRF

Author

Phil Chalmers rphilip.chalmers@gmail.com

Examples

if (FALSE) { # \dontrun{

# simulate data where group 2 has a smaller slopes and more extreme intercepts
set.seed(12345)
a1 <- a2 <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d1 <- d2 <- matrix(rnorm(15,0,.7),ncol=1)
a2[1:2, ] <- a1[1:2, ]/3
d1[c(1,3), ] <- d2[c(1,3), ]/4
head(data.frame(a.group1 = a1, a.group2 = a2, d.group1 = d1, d.group2 = d2))
itemtype <- rep('2PL', nrow(a1))
N <- 1000
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = .1, sigma = matrix(1.5))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))

#### no anchors, all items tested for DIF by adding item constrains one item at a time.
# define a parallel cluster (optional) to help speed up internal functions
if(interactive()) mirtCluster()

# Information matrix with Oakes' identity (not controlling for latent group differences)
# NOTE: Without properly equating the groups the following example code is not testing for DIF,
     # but instead reflects a combination of DIF + latent-trait distribution effects
model <- multipleGroup(dat, 1, group, SE = TRUE)

# Likelihood-ratio test for DIF (as well as model information)
dif <- DIF(model, c('a1', 'd'))
dif

# function silently includes "DIF_coefficients" attribute to view
# the IRT parameters post-completion
extract.mirt(dif, "DIF_coefficients")

# same as above, but using Wald tests with Benjamini & Hochberg adjustment
DIF(model, c('a1', 'd'), Wald = TRUE, p.adjust = 'fdr')

# equate the groups by assuming the last 5 items have no DIF
itemnames <- colnames(dat)
model <- multipleGroup(dat, 1, group, SE = TRUE,
   invariance = c(itemnames[11:ncol(dat)], 'free_means', 'free_var'))

# test whether adding slopes and intercepts constraints results in DIF. Plot items showing DIF
resulta1d <- DIF(model, c('a1', 'd'), plotdif = TRUE, items2test=1:10)
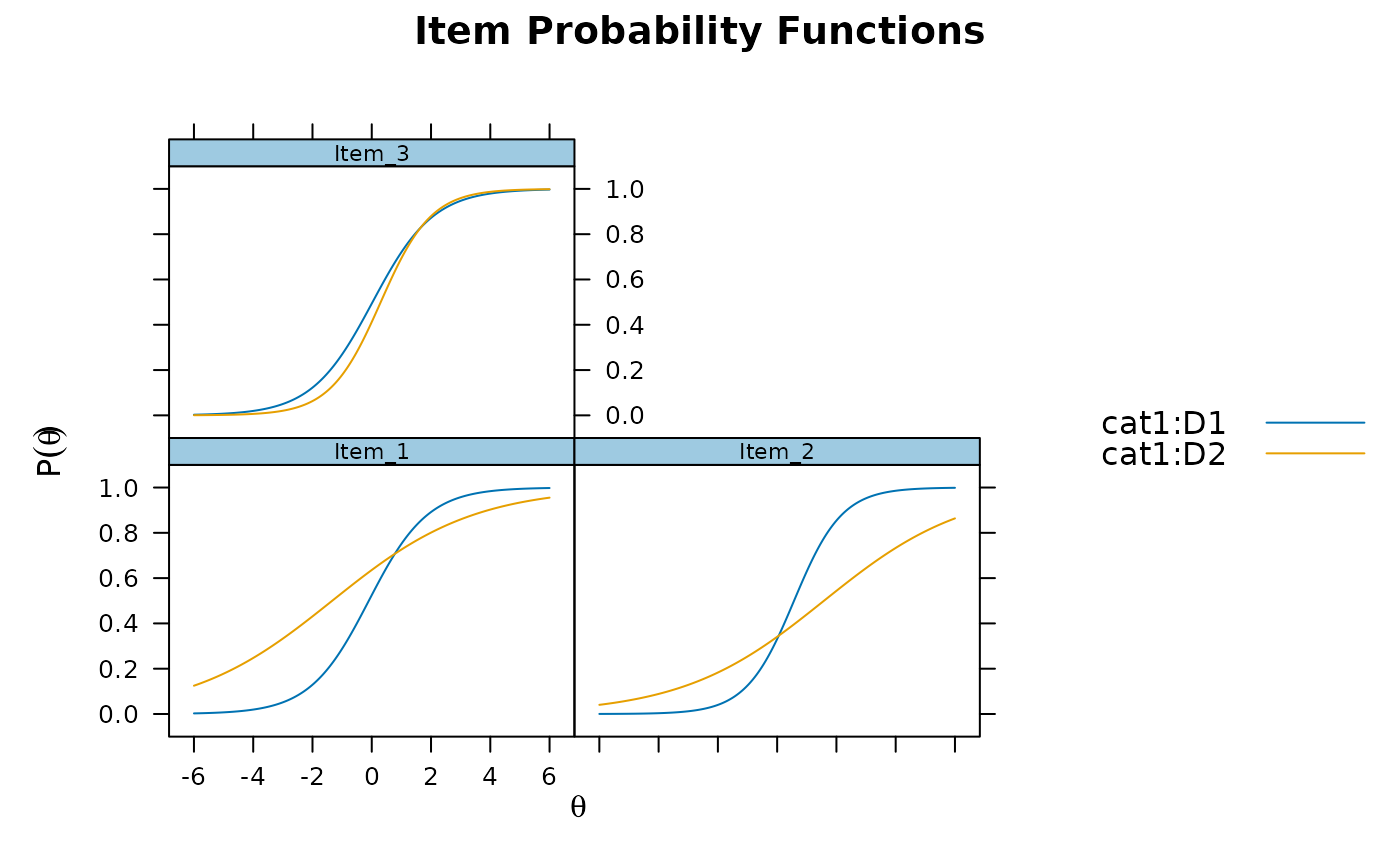resulta1d

# test whether adding only slope constraints results in DIF for all items
DIF(model, 'a1', items2test=1:10)

# Determine whether it's a1 or d parameter causing DIF (could be joint, however)
(a1s <- DIF(model, 'a1', items2test = 1:3))
(ds <- DIF(model, 'd', items2test = 1:3))

### drop down approach (freely estimating parameters across groups) when
### specifying a highly constrained model with estimated latent parameters
model_constrained <- multipleGroup(dat, 1, group,
  invariance = c(colnames(dat), 'free_means', 'free_var'))
dropdown <- DIF(model_constrained, c('a1', 'd'), scheme = 'drop')
dropdown

# View silent "DIF_coefficients" attribute
extract.mirt(dropdown, "DIF_coefficients")

### sequential schemes (add constraints)

### sequential searches using SABIC as the selection criteria
# starting from completely different models
stepup <- DIF(model, c('a1', 'd'), scheme = 'add_sequential',
              items2test=1:10)
stepup

# step down procedure for highly constrained model
stepdown <- DIF(model_constrained, c('a1', 'd'), scheme = 'drop_sequential')
stepdown

# view final MG model (only useful when scheme is 'add_sequential')
updated_mod <- DIF(model, c('a1', 'd'), scheme = 'add_sequential',
               return_seq_model=TRUE)
plot(updated_mod, type='trace')


###################################
# Multi-group example

a1 <- a2 <- a3 <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d1 <- d2 <- d3 <- matrix(rnorm(15,0,.7),ncol=1)
a2[1:2, ] <- a1[1:2, ]/3
d3[c(1,3), ] <- d2[c(1,3), ]/4
head(data.frame(a.group1 = a1, a.group2 = a2, a.group3 = a3,
                d.group1 = d1, d.group2 = d2, d.group3 = d3))
itemtype <- rep('2PL', nrow(a1))
N <- 1000
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = .1, sigma = matrix(1.5))
dataset3 <- simdata(a3, d3, N, itemtype, mu = .2)
dat <- rbind(dataset1, dataset2, dataset3)
group <- gl(3, N, labels = c('g1', 'g2', 'g3'))

# equate the groups by assuming the last 5 items have no DIF
itemnames <- colnames(dat)
model <- multipleGroup(dat, group=group, SE=TRUE,
   invariance = c(itemnames[11:ncol(dat)], 'free_means', 'free_var'))
coef(model, simplify=TRUE)

# omnibus tests
dif <- DIF(model, which.par = c('a1', 'd'), items2test=1:9)
dif

# pairwise post-hoc tests for items flagged via omnibus tests
dif.posthoc <- DIF(model, which.par = c('a1', 'd'), items2test=1:2,
                   pairwise = TRUE)
dif.posthoc

# further probing for df = 1 tests, this time with Wald tests
DIF(model, which.par = c('a1'), items2test=1:2, pairwise = TRUE,
    Wald=TRUE)
DIF(model, which.par = c('d'), items2test=1:2, pairwise = TRUE,
    Wald=TRUE)

} # }