Implements the set of fixed-item calibration methods described by Kim (2006). The initial
calibrated model must be fitted via mirt, is currently limited to
unidimensional models only, and should only be utilized when the new set of responses
are obtained from a population with similar distributional characteristics in the latent traits.
For more flexible calibration of items, including a fixed-item calibration variant involving
anchor items for equating, see multipleGroup.
Usage
fixedCalib(
data,
model = 1,
old_mod,
PAU = "MWU",
NEMC = "MEM",
technical = list(),
...
)Arguments
- data
new data to be used for calibration. Note that to be consistent with the
modobject, observed responses/NA placeholders must be included to link the item names used in the originalmoddefinition (i.e.,extract.mirt(mod, what = 'itemnames'))- model
type of model to fit for the complete dataset (not that for the fixed items in
old_modthe factor loadings/constraints specified by the potentialmirt.modelspecification is not relevant)- old_mod
a model of class SingleGroupClass fitted using
mirt- PAU
prior ability update (PAU) approach. Supports none (
"NWU"), one ("OWU"), and many ("MWU")- NEMC
number of EM cycles (NEMC) to use for the to-be-estimated parameters. Supports one (
"OEM") and many ("MEM")- technical
list of technical estimation arguments (see
mirtfor details)- ...
additional arguments to pass to
mirt
References
Kim, S. (2006). A comparative study of IRT fixed parameter calibration methods. Journal of Educational Measurement, 4(43), 355-381.
Examples
# \donttest{
# single factor
set.seed(12345)
J <- 50
a <- matrix(abs(rnorm(J,1,.3)), ncol=1)
d <- matrix(rnorm(J,0,.7),ncol=1)
itemtype <- rep('2PL', nrow(a))
# calibration data theta ~ N(0,1)
N <- 3000
dataset1 <- simdata(a, d, N = N, itemtype=itemtype)
# new data (again, theta ~ N(0,1))
dataset2 <- simdata(a, d, N = 1000, itemtype=itemtype)
# last 40% of experimental items not given to calibration group
# (unobserved; hence removed)
dataset1 <- dataset1[,-c(J:(J*.6))]
head(dataset1)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1,] 0 0 0 0 0 0 1 1 1 0
#> [2,] 0 0 0 1 0 1 0 0 0 0
#> [3,] 0 1 0 1 1 1 1 1 1 1
#> [4,] 0 1 1 0 1 0 0 0 1 0
#> [5,] 1 0 1 1 1 0 1 0 1 0
#> [6,] 1 1 0 1 0 1 0 1 1 0
#> Item_11 Item_12 Item_13 Item_14 Item_15 Item_16 Item_17 Item_18 Item_19
#> [1,] 1 1 1 1 1 0 0 0 1
#> [2,] 0 0 1 0 0 0 1 1 0
#> [3,] 1 1 0 1 0 1 0 0 0
#> [4,] 0 0 1 1 0 0 1 1 0
#> [5,] 0 0 0 1 0 0 1 1 1
#> [6,] 1 0 1 1 0 0 1 0 1
#> Item_20 Item_21 Item_22 Item_23 Item_24 Item_25 Item_26 Item_27 Item_28
#> [1,] 0 0 0 0 1 0 0 1 0
#> [2,] 0 1 0 0 1 0 0 1 1
#> [3,] 0 1 0 1 1 1 1 0 0
#> [4,] 0 0 0 0 0 1 0 1 0
#> [5,] 0 1 1 1 1 1 1 1 1
#> [6,] 0 0 0 1 1 1 0 0 0
#> Item_29
#> [1,] 1
#> [2,] 1
#> [3,] 1
#> [4,] 1
#> [5,] 1
#> [6,] 1
#--------------------------------------
# calibrated model from dataset1 only
mod <- mirt(dataset1, model = 1)
coef(mod, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
# No Prior Weights Updating and One EM Cycle (NWU-OEM)
NWU_OEM <- fixedCalib(dataset2, model=1, old_mod=mod, PAU='NWU', NEMC='OEM')
coef(NWU_OEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.750 1.329 0 1
#> Item_31 1.093 1.235 0 1
#> Item_32 1.380 1.740 0 1
#> Item_33 1.112 0.441 0 1
#> Item_34 1.164 2.443 0 1
#> Item_35 1.054 1.361 0 1
#> Item_36 0.863 1.818 0 1
#> Item_37 0.717 0.865 0 1
#> Item_38 0.379 0.044 0 1
#> Item_39 1.180 1.336 0 1
#> Item_40 0.713 0.967 0 1
#> Item_41 0.865 0.150 0 1
#> Item_42 0.205 -0.581 0 1
#> Item_43 0.587 1.914 0 1
#> Item_44 0.977 0.509 0 1
#> Item_45 0.944 -0.151 0 1
#> Item_46 1.239 1.288 0 1
#> Item_47 0.547 0.176 0 1
#> Item_48 0.811 2.059 0 1
#> Item_49 0.841 0.169 0 1
#> Item_50 0.631 -0.103 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(NWU_OEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.7503191 1.32941502 0.9513067 0.71488089
#> Item_31 1.0934852 1.23450251 1.2435620 0.45176815
#> Item_32 1.3797225 1.73968930 1.6590501 0.73020049
#> Item_33 1.1122063 0.44125253 1.6147571 -0.21305838
#> Item_34 1.1635528 2.44296521 1.4897337 1.73397764
#> Item_35 1.0542788 1.36075678 1.0762814 0.67985447
#> Item_36 0.8625460 1.81754474 1.1473565 1.30696943
#> Item_37 0.7169594 0.86486730 0.9027740 0.47042973
#> Item_38 0.3789943 0.04394555 0.5013849 -0.21556737
#> Item_39 1.1801729 1.33626718 1.5303202 0.37556660
#> Item_40 0.7130625 0.96707202 1.0077403 0.57740905
#> Item_41 0.8654027 0.14975466 1.3385533 -0.67473104
#> Item_42 0.2054520 -0.58087717 0.2858926 -0.59855776
#> Item_43 0.5870526 1.91384494 0.6819203 1.32086286
#> Item_44 0.9773758 0.50918361 1.2811422 -0.27427356
#> Item_45 0.9438821 -0.15062731 1.2563355 -0.68644306
#> Item_46 1.2394331 1.28838231 1.4382188 0.48113247
#> Item_47 0.5466966 0.17590264 0.5760704 -0.35353046
#> Item_48 0.8112318 2.05870733 1.1702210 1.51040387
#> Item_49 0.8414788 0.16883149 1.1749563 -0.41985829
#> Item_50 0.6307197 -0.10310709 0.6079603 -0.48618269
plot(NWU_OEM, type = 'empiricalhist')
 # No Prior Weights Updating and Multiple EM Cycles (NWU-MEM)
NWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod, PAU = 'NWU')
coef(NWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.976 0.738 0 1
#> Item_31 1.355 0.436 0 1
#> Item_32 1.896 0.751 0 1
#> Item_33 1.483 -0.136 0 1
#> Item_34 1.566 1.615 0 1
#> Item_35 1.108 0.689 0 1
#> Item_36 1.027 1.297 0 1
#> Item_37 0.950 0.485 0 1
#> Item_38 0.636 -0.358 0 1
#> Item_39 1.561 0.369 0 1
#> Item_40 1.002 0.572 0 1
#> Item_41 1.293 -0.537 0 1
#> Item_42 0.237 -0.569 0 1
#> Item_43 0.759 1.528 0 1
#> Item_44 1.267 -0.198 0 1
#> Item_45 1.179 -0.719 0 1
#> Item_46 1.484 0.418 0 1
#> Item_47 0.517 -0.350 0 1
#> Item_48 1.204 1.560 0 1
#> Item_49 1.178 -0.381 0 1
#> Item_50 0.611 -0.485 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(NWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9762030 0.73762603 0.9513067 0.71488089
#> Item_31 1.3546278 0.43608060 1.2435620 0.45176815
#> Item_32 1.8963614 0.75072559 1.6590501 0.73020049
#> Item_33 1.4833684 -0.13615393 1.6147571 -0.21305838
#> Item_34 1.5661380 1.61503162 1.4897337 1.73397764
#> Item_35 1.1080231 0.68889209 1.0762814 0.67985447
#> Item_36 1.0265916 1.29656964 1.1473565 1.30696943
#> Item_37 0.9495227 0.48504809 0.9027740 0.47042973
#> Item_38 0.6357917 -0.35821345 0.5013849 -0.21556737
#> Item_39 1.5609002 0.36934080 1.5303202 0.37556660
#> Item_40 1.0017413 0.57214795 1.0077403 0.57740905
#> Item_41 1.2934463 -0.53663846 1.3385533 -0.67473104
#> Item_42 0.2365342 -0.56867576 0.2858926 -0.59855776
#> Item_43 0.7585749 1.52822491 0.6819203 1.32086286
#> Item_44 1.2665593 -0.19834384 1.2811422 -0.27427356
#> Item_45 1.1786531 -0.71904132 1.2563355 -0.68644306
#> Item_46 1.4839823 0.41813815 1.4382188 0.48113247
#> Item_47 0.5165255 -0.35006720 0.5760704 -0.35353046
#> Item_48 1.2040324 1.55971466 1.1702210 1.51040387
#> Item_49 1.1779999 -0.38145049 1.1749563 -0.41985829
#> Item_50 0.6105721 -0.48525352 0.6079603 -0.48618269
plot(NWU_MEM, type = 'empiricalhist')
# No Prior Weights Updating and Multiple EM Cycles (NWU-MEM)
NWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod, PAU = 'NWU')
coef(NWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.976 0.738 0 1
#> Item_31 1.355 0.436 0 1
#> Item_32 1.896 0.751 0 1
#> Item_33 1.483 -0.136 0 1
#> Item_34 1.566 1.615 0 1
#> Item_35 1.108 0.689 0 1
#> Item_36 1.027 1.297 0 1
#> Item_37 0.950 0.485 0 1
#> Item_38 0.636 -0.358 0 1
#> Item_39 1.561 0.369 0 1
#> Item_40 1.002 0.572 0 1
#> Item_41 1.293 -0.537 0 1
#> Item_42 0.237 -0.569 0 1
#> Item_43 0.759 1.528 0 1
#> Item_44 1.267 -0.198 0 1
#> Item_45 1.179 -0.719 0 1
#> Item_46 1.484 0.418 0 1
#> Item_47 0.517 -0.350 0 1
#> Item_48 1.204 1.560 0 1
#> Item_49 1.178 -0.381 0 1
#> Item_50 0.611 -0.485 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(NWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9762030 0.73762603 0.9513067 0.71488089
#> Item_31 1.3546278 0.43608060 1.2435620 0.45176815
#> Item_32 1.8963614 0.75072559 1.6590501 0.73020049
#> Item_33 1.4833684 -0.13615393 1.6147571 -0.21305838
#> Item_34 1.5661380 1.61503162 1.4897337 1.73397764
#> Item_35 1.1080231 0.68889209 1.0762814 0.67985447
#> Item_36 1.0265916 1.29656964 1.1473565 1.30696943
#> Item_37 0.9495227 0.48504809 0.9027740 0.47042973
#> Item_38 0.6357917 -0.35821345 0.5013849 -0.21556737
#> Item_39 1.5609002 0.36934080 1.5303202 0.37556660
#> Item_40 1.0017413 0.57214795 1.0077403 0.57740905
#> Item_41 1.2934463 -0.53663846 1.3385533 -0.67473104
#> Item_42 0.2365342 -0.56867576 0.2858926 -0.59855776
#> Item_43 0.7585749 1.52822491 0.6819203 1.32086286
#> Item_44 1.2665593 -0.19834384 1.2811422 -0.27427356
#> Item_45 1.1786531 -0.71904132 1.2563355 -0.68644306
#> Item_46 1.4839823 0.41813815 1.4382188 0.48113247
#> Item_47 0.5165255 -0.35006720 0.5760704 -0.35353046
#> Item_48 1.2040324 1.55971466 1.1702210 1.51040387
#> Item_49 1.1779999 -0.38145049 1.1749563 -0.41985829
#> Item_50 0.6105721 -0.48525352 0.6079603 -0.48618269
plot(NWU_MEM, type = 'empiricalhist')
 # One Prior Weights Updating and One EM Cycle (OWU-OEM)
OWU_OEM <- fixedCalib(dataset2, model=1, old_mod=mod, PAU='OWU', NEMC="OEM")
coef(OWU_OEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.734 1.342 0 1
#> Item_31 1.081 1.235 0 1
#> Item_32 1.354 1.740 0 1
#> Item_33 1.087 0.449 0 1
#> Item_34 1.180 2.469 0 1
#> Item_35 1.080 1.352 0 1
#> Item_36 0.867 1.826 0 1
#> Item_37 0.736 0.845 0 1
#> Item_38 0.407 0.018 0 1
#> Item_39 1.192 1.330 0 1
#> Item_40 0.694 0.970 0 1
#> Item_41 0.876 0.141 0 1
#> Item_42 0.207 -0.593 0 1
#> Item_43 0.608 1.915 0 1
#> Item_44 0.948 0.525 0 1
#> Item_45 0.918 -0.150 0 1
#> Item_46 1.246 1.287 0 1
#> Item_47 0.541 0.194 0 1
#> Item_48 0.824 2.052 0 1
#> Item_49 0.881 0.150 0 1
#> Item_50 0.643 -0.109 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(OWU_OEM, simplify=TRUE)$items[,c('a1','d')], pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.7338596 1.34171621 0.9513067 0.71488089
#> Item_31 1.0810934 1.23518942 1.2435620 0.45176815
#> Item_32 1.3536031 1.74007904 1.6590501 0.73020049
#> Item_33 1.0871425 0.44941021 1.6147571 -0.21305838
#> Item_34 1.1800858 2.46871234 1.4897337 1.73397764
#> Item_35 1.0803263 1.35175673 1.0762814 0.67985447
#> Item_36 0.8666080 1.82586462 1.1473565 1.30696943
#> Item_37 0.7358795 0.84485396 0.9027740 0.47042973
#> Item_38 0.4070019 0.01833533 0.5013849 -0.21556737
#> Item_39 1.1921382 1.33027311 1.5303202 0.37556660
#> Item_40 0.6941284 0.97027712 1.0077403 0.57740905
#> Item_41 0.8759719 0.14117791 1.3385533 -0.67473104
#> Item_42 0.2070009 -0.59318726 0.2858926 -0.59855776
#> Item_43 0.6082669 1.91531663 0.6819203 1.32086286
#> Item_44 0.9481219 0.52535227 1.2811422 -0.27427356
#> Item_45 0.9181546 -0.15002032 1.2563355 -0.68644306
#> Item_46 1.2461867 1.28672335 1.4382188 0.48113247
#> Item_47 0.5414343 0.19387196 0.5760704 -0.35353046
#> Item_48 0.8238261 2.05156006 1.1702210 1.51040387
#> Item_49 0.8809591 0.15027203 1.1749563 -0.41985829
#> Item_50 0.6425456 -0.10887582 0.6079603 -0.48618269
plot(OWU_OEM, type = 'empiricalhist')
# One Prior Weights Updating and One EM Cycle (OWU-OEM)
OWU_OEM <- fixedCalib(dataset2, model=1, old_mod=mod, PAU='OWU', NEMC="OEM")
coef(OWU_OEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.734 1.342 0 1
#> Item_31 1.081 1.235 0 1
#> Item_32 1.354 1.740 0 1
#> Item_33 1.087 0.449 0 1
#> Item_34 1.180 2.469 0 1
#> Item_35 1.080 1.352 0 1
#> Item_36 0.867 1.826 0 1
#> Item_37 0.736 0.845 0 1
#> Item_38 0.407 0.018 0 1
#> Item_39 1.192 1.330 0 1
#> Item_40 0.694 0.970 0 1
#> Item_41 0.876 0.141 0 1
#> Item_42 0.207 -0.593 0 1
#> Item_43 0.608 1.915 0 1
#> Item_44 0.948 0.525 0 1
#> Item_45 0.918 -0.150 0 1
#> Item_46 1.246 1.287 0 1
#> Item_47 0.541 0.194 0 1
#> Item_48 0.824 2.052 0 1
#> Item_49 0.881 0.150 0 1
#> Item_50 0.643 -0.109 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(OWU_OEM, simplify=TRUE)$items[,c('a1','d')], pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.7338596 1.34171621 0.9513067 0.71488089
#> Item_31 1.0810934 1.23518942 1.2435620 0.45176815
#> Item_32 1.3536031 1.74007904 1.6590501 0.73020049
#> Item_33 1.0871425 0.44941021 1.6147571 -0.21305838
#> Item_34 1.1800858 2.46871234 1.4897337 1.73397764
#> Item_35 1.0803263 1.35175673 1.0762814 0.67985447
#> Item_36 0.8666080 1.82586462 1.1473565 1.30696943
#> Item_37 0.7358795 0.84485396 0.9027740 0.47042973
#> Item_38 0.4070019 0.01833533 0.5013849 -0.21556737
#> Item_39 1.1921382 1.33027311 1.5303202 0.37556660
#> Item_40 0.6941284 0.97027712 1.0077403 0.57740905
#> Item_41 0.8759719 0.14117791 1.3385533 -0.67473104
#> Item_42 0.2070009 -0.59318726 0.2858926 -0.59855776
#> Item_43 0.6082669 1.91531663 0.6819203 1.32086286
#> Item_44 0.9481219 0.52535227 1.2811422 -0.27427356
#> Item_45 0.9181546 -0.15002032 1.2563355 -0.68644306
#> Item_46 1.2461867 1.28672335 1.4382188 0.48113247
#> Item_47 0.5414343 0.19387196 0.5760704 -0.35353046
#> Item_48 0.8238261 2.05156006 1.1702210 1.51040387
#> Item_49 0.8809591 0.15027203 1.1749563 -0.41985829
#> Item_50 0.6425456 -0.10887582 0.6079603 -0.48618269
plot(OWU_OEM, type = 'empiricalhist')
 # One Prior Weights Updating and Multiple EM Cycles (OWU-MEM)
OWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod, PAU = 'OWU')
coef(OWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.975 0.738 0 1
#> Item_31 1.353 0.436 0 1
#> Item_32 1.892 0.749 0 1
#> Item_33 1.482 -0.137 0 1
#> Item_34 1.563 1.614 0 1
#> Item_35 1.107 0.689 0 1
#> Item_36 1.026 1.297 0 1
#> Item_37 0.949 0.485 0 1
#> Item_38 0.637 -0.358 0 1
#> Item_39 1.559 0.369 0 1
#> Item_40 1.001 0.572 0 1
#> Item_41 1.294 -0.537 0 1
#> Item_42 0.237 -0.569 0 1
#> Item_43 0.758 1.528 0 1
#> Item_44 1.266 -0.199 0 1
#> Item_45 1.179 -0.719 0 1
#> Item_46 1.482 0.418 0 1
#> Item_47 0.517 -0.350 0 1
#> Item_48 1.203 1.560 0 1
#> Item_49 1.178 -0.382 0 1
#> Item_50 0.611 -0.485 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(OWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9754835 0.73759996 0.9513067 0.71488089
#> Item_31 1.3529960 0.43565857 1.2435620 0.45176815
#> Item_32 1.8920655 0.74941926 1.6590501 0.73020049
#> Item_33 1.4823957 -0.13676561 1.6147571 -0.21305838
#> Item_34 1.5632963 1.61443582 1.4897337 1.73397764
#> Item_35 1.1070549 0.68876441 1.0762814 0.67985447
#> Item_36 1.0257494 1.29658002 1.1473565 1.30696943
#> Item_37 0.9487642 0.48500521 0.9027740 0.47042973
#> Item_38 0.6365371 -0.35814281 0.5013849 -0.21556737
#> Item_39 1.5587391 0.36866684 1.5303202 0.37556660
#> Item_40 1.0011701 0.57211468 1.0077403 0.57740905
#> Item_41 1.2936486 -0.53716279 1.3385533 -0.67473104
#> Item_42 0.2372635 -0.56862885 0.2858926 -0.59855776
#> Item_43 0.7581178 1.52829512 0.6819203 1.32086286
#> Item_44 1.2655570 -0.19867816 1.2811422 -0.27427356
#> Item_45 1.1789916 -0.71942555 1.2563355 -0.68644306
#> Item_46 1.4820218 0.41756426 1.4382188 0.48113247
#> Item_47 0.5174459 -0.34998852 0.5760704 -0.35353046
#> Item_48 1.2029294 1.55973508 1.1702210 1.51040387
#> Item_49 1.1780664 -0.38178278 1.1749563 -0.41985829
#> Item_50 0.6113326 -0.48518034 0.6079603 -0.48618269
plot(OWU_MEM, type = 'empiricalhist')
# One Prior Weights Updating and Multiple EM Cycles (OWU-MEM)
OWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod, PAU = 'OWU')
coef(OWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.975 0.738 0 1
#> Item_31 1.353 0.436 0 1
#> Item_32 1.892 0.749 0 1
#> Item_33 1.482 -0.137 0 1
#> Item_34 1.563 1.614 0 1
#> Item_35 1.107 0.689 0 1
#> Item_36 1.026 1.297 0 1
#> Item_37 0.949 0.485 0 1
#> Item_38 0.637 -0.358 0 1
#> Item_39 1.559 0.369 0 1
#> Item_40 1.001 0.572 0 1
#> Item_41 1.294 -0.537 0 1
#> Item_42 0.237 -0.569 0 1
#> Item_43 0.758 1.528 0 1
#> Item_44 1.266 -0.199 0 1
#> Item_45 1.179 -0.719 0 1
#> Item_46 1.482 0.418 0 1
#> Item_47 0.517 -0.350 0 1
#> Item_48 1.203 1.560 0 1
#> Item_49 1.178 -0.382 0 1
#> Item_50 0.611 -0.485 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(OWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9754835 0.73759996 0.9513067 0.71488089
#> Item_31 1.3529960 0.43565857 1.2435620 0.45176815
#> Item_32 1.8920655 0.74941926 1.6590501 0.73020049
#> Item_33 1.4823957 -0.13676561 1.6147571 -0.21305838
#> Item_34 1.5632963 1.61443582 1.4897337 1.73397764
#> Item_35 1.1070549 0.68876441 1.0762814 0.67985447
#> Item_36 1.0257494 1.29658002 1.1473565 1.30696943
#> Item_37 0.9487642 0.48500521 0.9027740 0.47042973
#> Item_38 0.6365371 -0.35814281 0.5013849 -0.21556737
#> Item_39 1.5587391 0.36866684 1.5303202 0.37556660
#> Item_40 1.0011701 0.57211468 1.0077403 0.57740905
#> Item_41 1.2936486 -0.53716279 1.3385533 -0.67473104
#> Item_42 0.2372635 -0.56862885 0.2858926 -0.59855776
#> Item_43 0.7581178 1.52829512 0.6819203 1.32086286
#> Item_44 1.2655570 -0.19867816 1.2811422 -0.27427356
#> Item_45 1.1789916 -0.71942555 1.2563355 -0.68644306
#> Item_46 1.4820218 0.41756426 1.4382188 0.48113247
#> Item_47 0.5174459 -0.34998852 0.5760704 -0.35353046
#> Item_48 1.2029294 1.55973508 1.1702210 1.51040387
#> Item_49 1.1780664 -0.38178278 1.1749563 -0.41985829
#> Item_50 0.6113326 -0.48518034 0.6079603 -0.48618269
plot(OWU_MEM, type = 'empiricalhist')
 # Multiple Prior Weights Updating and Multiple EM Cycles (MWU-MEM)
MWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod)
coef(MWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.979 0.736 0 1
#> Item_31 1.356 0.434 0 1
#> Item_32 1.901 0.748 0 1
#> Item_33 1.486 -0.138 0 1
#> Item_34 1.571 1.614 0 1
#> Item_35 1.110 0.687 0 1
#> Item_36 1.033 1.297 0 1
#> Item_37 0.952 0.484 0 1
#> Item_38 0.642 -0.359 0 1
#> Item_39 1.565 0.367 0 1
#> Item_40 1.006 0.571 0 1
#> Item_41 1.299 -0.539 0 1
#> Item_42 0.241 -0.569 0 1
#> Item_43 0.763 1.528 0 1
#> Item_44 1.269 -0.200 0 1
#> Item_45 1.180 -0.720 0 1
#> Item_46 1.488 0.416 0 1
#> Item_47 0.523 -0.351 0 1
#> Item_48 1.209 1.559 0 1
#> Item_49 1.182 -0.383 0 1
#> Item_50 0.616 -0.486 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(MWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9791660 0.73649261 0.9513067 0.71488089
#> Item_31 1.3557620 0.43401149 1.2435620 0.45176815
#> Item_32 1.9007882 0.74806045 1.6590501 0.73020049
#> Item_33 1.4862529 -0.13819824 1.6147571 -0.21305838
#> Item_34 1.5713559 1.61388772 1.4897337 1.73397764
#> Item_35 1.1101719 0.68737052 1.0762814 0.67985447
#> Item_36 1.0330416 1.29655187 1.1473565 1.30696943
#> Item_37 0.9517934 0.48386436 0.9027740 0.47042973
#> Item_38 0.6415895 -0.35896158 0.5013849 -0.21556737
#> Item_39 1.5653049 0.36728263 1.5303202 0.37556660
#> Item_40 1.0055938 0.57108702 1.0077403 0.57740905
#> Item_41 1.2988445 -0.53887261 1.3385533 -0.67473104
#> Item_42 0.2407043 -0.56898111 0.2858926 -0.59855776
#> Item_43 0.7634191 1.52801497 0.6819203 1.32086286
#> Item_44 1.2688454 -0.20002553 1.2811422 -0.27427356
#> Item_45 1.1799250 -0.72019334 1.2563355 -0.68644306
#> Item_46 1.4880374 0.41618563 1.4382188 0.48113247
#> Item_47 0.5228163 -0.35071973 0.5760704 -0.35353046
#> Item_48 1.2091851 1.55916704 1.1702210 1.51040387
#> Item_49 1.1823034 -0.38320022 1.1749563 -0.41985829
#> Item_50 0.6156231 -0.48588671 0.6079603 -0.48618269
plot(MWU_MEM, type = 'empiricalhist')
# Multiple Prior Weights Updating and Multiple EM Cycles (MWU-MEM)
MWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod)
coef(MWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 0.979 0.736 0 1
#> Item_31 1.356 0.434 0 1
#> Item_32 1.901 0.748 0 1
#> Item_33 1.486 -0.138 0 1
#> Item_34 1.571 1.614 0 1
#> Item_35 1.110 0.687 0 1
#> Item_36 1.033 1.297 0 1
#> Item_37 0.952 0.484 0 1
#> Item_38 0.642 -0.359 0 1
#> Item_39 1.565 0.367 0 1
#> Item_40 1.006 0.571 0 1
#> Item_41 1.299 -0.539 0 1
#> Item_42 0.241 -0.569 0 1
#> Item_43 0.763 1.528 0 1
#> Item_44 1.269 -0.200 0 1
#> Item_45 1.180 -0.720 0 1
#> Item_46 1.488 0.416 0 1
#> Item_47 0.523 -0.351 0 1
#> Item_48 1.209 1.559 0 1
#> Item_49 1.182 -0.383 0 1
#> Item_50 0.616 -0.486 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(MWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 0.9791660 0.73649261 0.9513067 0.71488089
#> Item_31 1.3557620 0.43401149 1.2435620 0.45176815
#> Item_32 1.9007882 0.74806045 1.6590501 0.73020049
#> Item_33 1.4862529 -0.13819824 1.6147571 -0.21305838
#> Item_34 1.5713559 1.61388772 1.4897337 1.73397764
#> Item_35 1.1101719 0.68737052 1.0762814 0.67985447
#> Item_36 1.0330416 1.29655187 1.1473565 1.30696943
#> Item_37 0.9517934 0.48386436 0.9027740 0.47042973
#> Item_38 0.6415895 -0.35896158 0.5013849 -0.21556737
#> Item_39 1.5653049 0.36728263 1.5303202 0.37556660
#> Item_40 1.0055938 0.57108702 1.0077403 0.57740905
#> Item_41 1.2988445 -0.53887261 1.3385533 -0.67473104
#> Item_42 0.2407043 -0.56898111 0.2858926 -0.59855776
#> Item_43 0.7634191 1.52801497 0.6819203 1.32086286
#> Item_44 1.2688454 -0.20002553 1.2811422 -0.27427356
#> Item_45 1.1799250 -0.72019334 1.2563355 -0.68644306
#> Item_46 1.4880374 0.41618563 1.4382188 0.48113247
#> Item_47 0.5228163 -0.35071973 0.5760704 -0.35353046
#> Item_48 1.2091851 1.55916704 1.1702210 1.51040387
#> Item_49 1.1823034 -0.38320022 1.1749563 -0.41985829
#> Item_50 0.6156231 -0.48588671 0.6079603 -0.48618269
plot(MWU_MEM, type = 'empiricalhist')
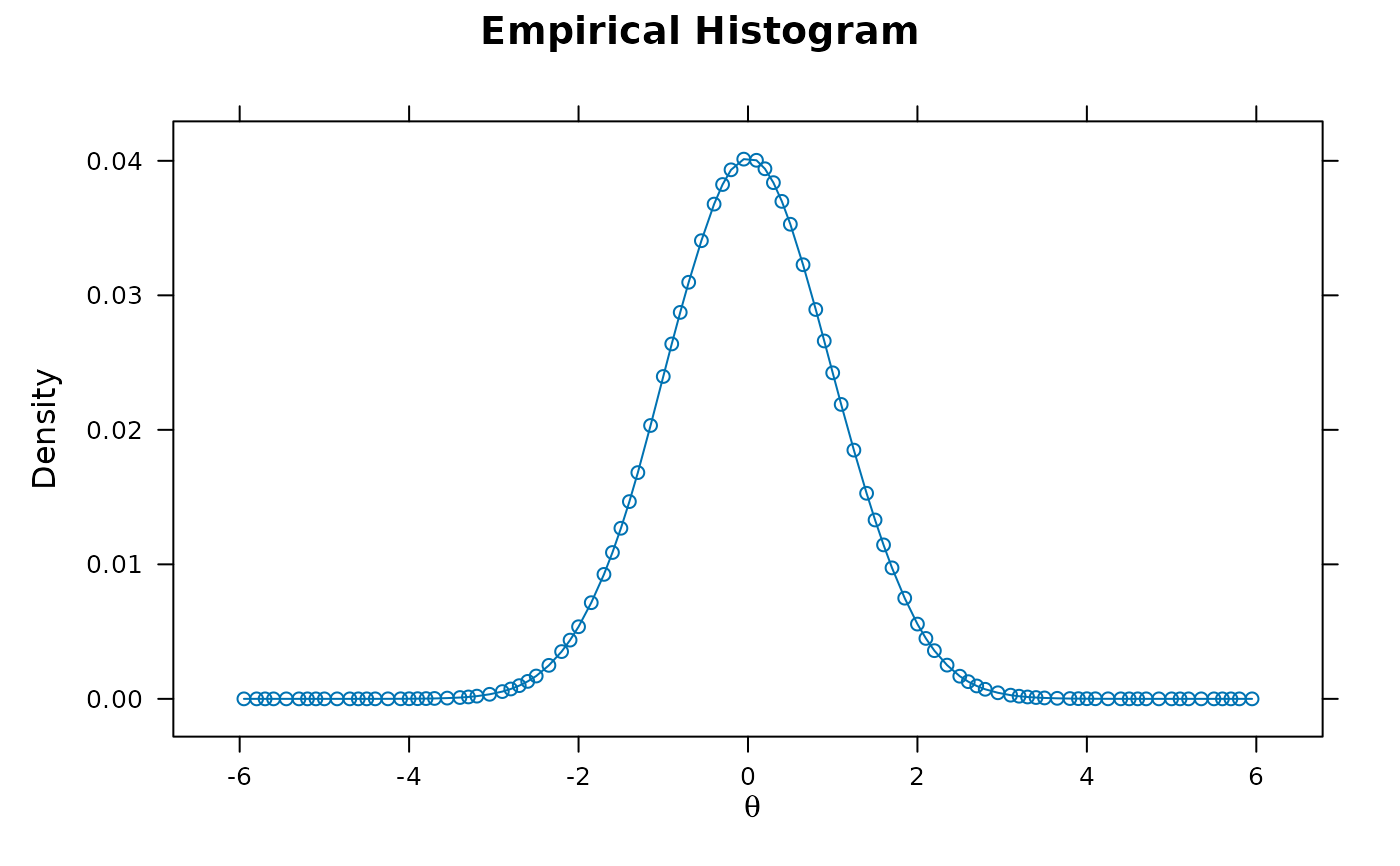 # factor scores distribution check
fs <- fscores(MWU_MEM)
hist(fs)
# factor scores distribution check
fs <- fscores(MWU_MEM)
hist(fs)
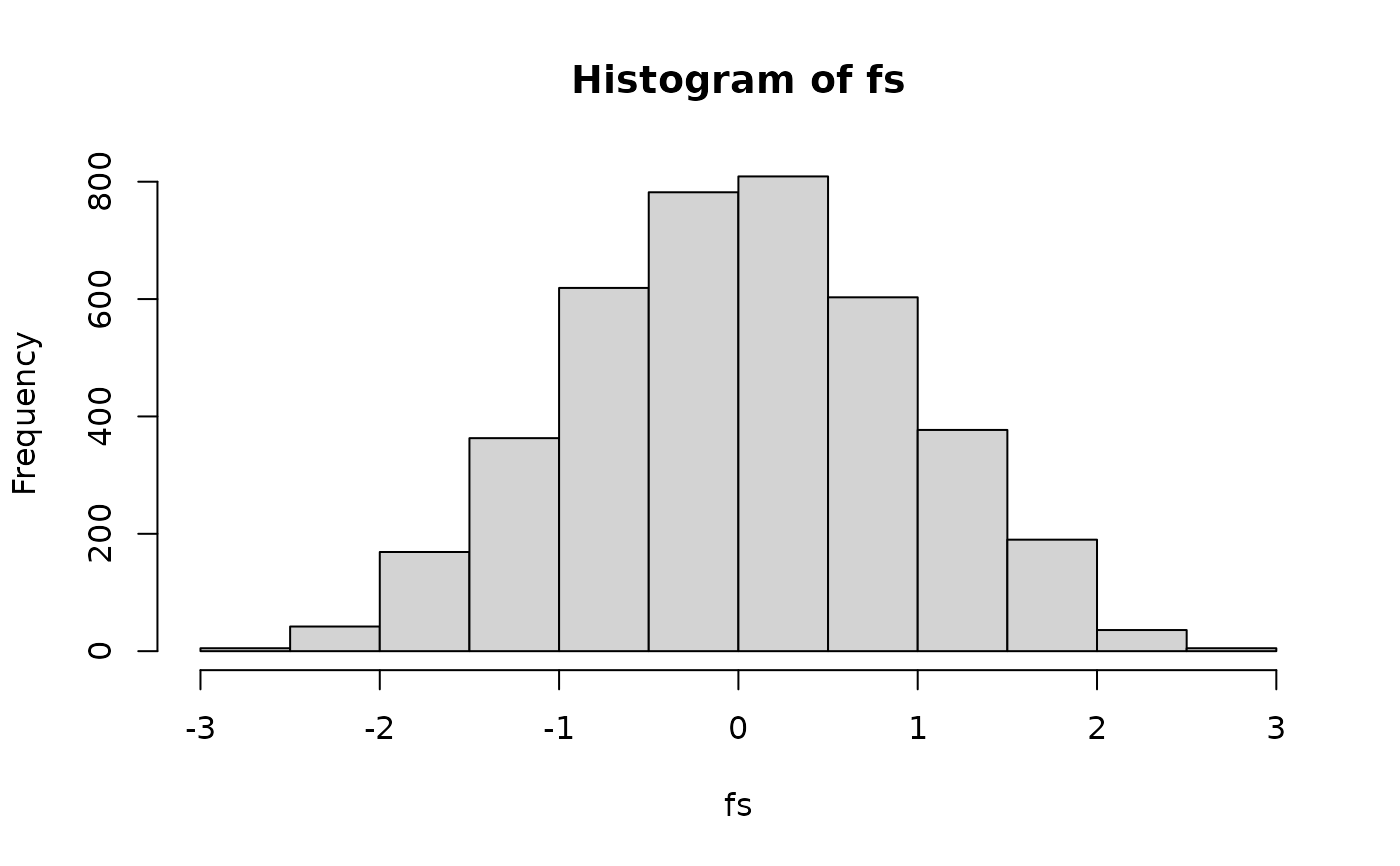 c(mean_calib=mean(fs[1:N, ]), sd_calib=sd(fs[1:N, ]))
#> mean_calib sd_calib
#> -0.0001434688 0.9215504578
c(mean_exper=mean(fs[-c(1:N), ]), sd_exper=sd(fs[-c(1:N), ]))
#> mean_exper sd_exper
#> 0.03352674 0.93335579
############################
## Item length constraint example for each participant in the experimental
## items group. In this example, all participants were forced to have a test
## length of J=30, though the item pool had J=50 total items.
# new experimental data (relatively extreme, theta ~ N(.5,1.5))
dataset2 <- simdata(a, d, N = 1000, itemtype=itemtype,
mu=.5, sigma=matrix(1.5))
# Add missing values to each participant in new dataset where individuals
# were randomly administered 10 experimental items, subject to the constraint
# that each participant received a test with J=30 items.
dataset2 <- t(apply(dataset2, 1, function(x){
NA_precalib <- sample(1:30, 10)
NA_experimental <- sample(31:50, 10)
x[c(NA_precalib, NA_experimental)] <- NA
x
}))
head(dataset2)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1,] NA 1 0 0 NA NA 0 NA 1 0
#> [2,] NA NA NA 1 1 1 NA 0 1 NA
#> [3,] NA NA 0 1 1 1 1 NA 1 0
#> [4,] NA 1 1 NA 0 NA 1 1 1 1
#> [5,] 1 1 1 1 NA NA 0 1 NA NA
#> [6,] 1 0 0 1 1 1 NA NA NA 0
#> Item_11 Item_12 Item_13 Item_14 Item_15 Item_16 Item_17 Item_18 Item_19
#> [1,] 1 0 NA 0 NA 0 0 1 0
#> [2,] 1 1 1 NA 0 0 1 NA 1
#> [3,] 1 1 0 1 1 1 NA NA NA
#> [4,] NA NA 1 NA 0 0 1 0 0
#> [5,] 1 NA 0 1 1 0 1 1 NA
#> [6,] 0 1 1 1 0 0 NA 1 NA
#> Item_20 Item_21 Item_22 Item_23 Item_24 Item_25 Item_26 Item_27 Item_28
#> [1,] 0 0 NA 0 1 NA 0 1 0
#> [2,] NA 0 1 NA 1 1 1 1 0
#> [3,] 1 1 NA 0 NA NA 1 NA 1
#> [4,] 1 1 1 NA NA 1 1 1 1
#> [5,] 1 NA 1 NA 1 NA NA 0 1
#> [6,] 1 1 0 0 0 NA NA NA 0
#> Item_29 Item_30 Item_31 Item_32 Item_33 Item_34 Item_35 Item_36 Item_37
#> [1,] NA NA 0 1 1 NA 0 NA 0
#> [2,] NA 1 1 NA NA 1 NA 1 1
#> [3,] 1 1 1 NA NA NA NA 1 NA
#> [4,] NA NA NA NA NA NA 0 NA 1
#> [5,] 1 1 NA 1 NA 1 1 NA NA
#> [6,] NA NA NA 1 NA NA 1 1 0
#> Item_38 Item_39 Item_40 Item_41 Item_42 Item_43 Item_44 Item_45 Item_46
#> [1,] 0 NA NA NA NA 1 0 NA 0
#> [2,] NA NA NA 1 NA 1 1 1 1
#> [3,] 1 NA NA NA 1 0 1 NA NA
#> [4,] 0 1 NA NA NA NA 1 1 0
#> [5,] NA 1 1 NA NA 1 NA NA 1
#> [6,] 1 NA NA NA NA 1 NA NA 1
#> Item_47 Item_48 Item_49 Item_50
#> [1,] NA NA 0 NA
#> [2,] NA 1 NA NA
#> [3,] 0 0 1 1
#> [4,] NA 1 0 1
#> [5,] NA 1 1 1
#> [6,] 0 1 NA 1
# check that all individuals had 30 items
all(rowSums(!is.na(dataset2)) == 30)
#> [1] TRUE
# Multiple Prior Weights Updating and Multiple EM Cycles (MWU-MEM)
MWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod)
coef(MWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 1.074 1.010 0 1
#> Item_31 1.416 0.729 0 1
#> Item_32 2.098 0.853 0 1
#> Item_33 1.622 0.025 0 1
#> Item_34 1.242 1.731 0 1
#> Item_35 1.127 0.868 0 1
#> Item_36 1.212 1.155 0 1
#> Item_37 1.022 0.621 0 1
#> Item_38 0.654 -0.203 0 1
#> Item_39 1.333 0.685 0 1
#> Item_40 0.939 0.678 0 1
#> Item_41 1.833 -0.565 0 1
#> Item_42 0.387 -0.631 0 1
#> Item_43 0.691 1.108 0 1
#> Item_44 1.232 -0.054 0 1
#> Item_45 1.105 -0.460 0 1
#> Item_46 1.401 0.694 0 1
#> Item_47 0.532 -0.290 0 1
#> Item_48 1.122 1.509 0 1
#> Item_49 1.158 -0.318 0 1
#> Item_50 0.692 -0.432 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(MWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 1.0736650 1.01026900 0.9513067 0.71488089
#> Item_31 1.4162584 0.72856155 1.2435620 0.45176815
#> Item_32 2.0975461 0.85255109 1.6590501 0.73020049
#> Item_33 1.6216973 0.02486148 1.6147571 -0.21305838
#> Item_34 1.2421629 1.73077613 1.4897337 1.73397764
#> Item_35 1.1268922 0.86756137 1.0762814 0.67985447
#> Item_36 1.2121379 1.15479360 1.1473565 1.30696943
#> Item_37 1.0218142 0.62136695 0.9027740 0.47042973
#> Item_38 0.6544987 -0.20307537 0.5013849 -0.21556737
#> Item_39 1.3326681 0.68465299 1.5303202 0.37556660
#> Item_40 0.9387813 0.67776738 1.0077403 0.57740905
#> Item_41 1.8326249 -0.56461189 1.3385533 -0.67473104
#> Item_42 0.3866839 -0.63085106 0.2858926 -0.59855776
#> Item_43 0.6911816 1.10845312 0.6819203 1.32086286
#> Item_44 1.2321139 -0.05383912 1.2811422 -0.27427356
#> Item_45 1.1045328 -0.45957575 1.2563355 -0.68644306
#> Item_46 1.4012118 0.69353524 1.4382188 0.48113247
#> Item_47 0.5324164 -0.28980316 0.5760704 -0.35353046
#> Item_48 1.1215187 1.50886830 1.1702210 1.51040387
#> Item_49 1.1583841 -0.31781501 1.1749563 -0.41985829
#> Item_50 0.6916807 -0.43180765 0.6079603 -0.48618269
plot(MWU_MEM, type = 'empiricalhist')
c(mean_calib=mean(fs[1:N, ]), sd_calib=sd(fs[1:N, ]))
#> mean_calib sd_calib
#> -0.0001434688 0.9215504578
c(mean_exper=mean(fs[-c(1:N), ]), sd_exper=sd(fs[-c(1:N), ]))
#> mean_exper sd_exper
#> 0.03352674 0.93335579
############################
## Item length constraint example for each participant in the experimental
## items group. In this example, all participants were forced to have a test
## length of J=30, though the item pool had J=50 total items.
# new experimental data (relatively extreme, theta ~ N(.5,1.5))
dataset2 <- simdata(a, d, N = 1000, itemtype=itemtype,
mu=.5, sigma=matrix(1.5))
# Add missing values to each participant in new dataset where individuals
# were randomly administered 10 experimental items, subject to the constraint
# that each participant received a test with J=30 items.
dataset2 <- t(apply(dataset2, 1, function(x){
NA_precalib <- sample(1:30, 10)
NA_experimental <- sample(31:50, 10)
x[c(NA_precalib, NA_experimental)] <- NA
x
}))
head(dataset2)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1,] NA 1 0 0 NA NA 0 NA 1 0
#> [2,] NA NA NA 1 1 1 NA 0 1 NA
#> [3,] NA NA 0 1 1 1 1 NA 1 0
#> [4,] NA 1 1 NA 0 NA 1 1 1 1
#> [5,] 1 1 1 1 NA NA 0 1 NA NA
#> [6,] 1 0 0 1 1 1 NA NA NA 0
#> Item_11 Item_12 Item_13 Item_14 Item_15 Item_16 Item_17 Item_18 Item_19
#> [1,] 1 0 NA 0 NA 0 0 1 0
#> [2,] 1 1 1 NA 0 0 1 NA 1
#> [3,] 1 1 0 1 1 1 NA NA NA
#> [4,] NA NA 1 NA 0 0 1 0 0
#> [5,] 1 NA 0 1 1 0 1 1 NA
#> [6,] 0 1 1 1 0 0 NA 1 NA
#> Item_20 Item_21 Item_22 Item_23 Item_24 Item_25 Item_26 Item_27 Item_28
#> [1,] 0 0 NA 0 1 NA 0 1 0
#> [2,] NA 0 1 NA 1 1 1 1 0
#> [3,] 1 1 NA 0 NA NA 1 NA 1
#> [4,] 1 1 1 NA NA 1 1 1 1
#> [5,] 1 NA 1 NA 1 NA NA 0 1
#> [6,] 1 1 0 0 0 NA NA NA 0
#> Item_29 Item_30 Item_31 Item_32 Item_33 Item_34 Item_35 Item_36 Item_37
#> [1,] NA NA 0 1 1 NA 0 NA 0
#> [2,] NA 1 1 NA NA 1 NA 1 1
#> [3,] 1 1 1 NA NA NA NA 1 NA
#> [4,] NA NA NA NA NA NA 0 NA 1
#> [5,] 1 1 NA 1 NA 1 1 NA NA
#> [6,] NA NA NA 1 NA NA 1 1 0
#> Item_38 Item_39 Item_40 Item_41 Item_42 Item_43 Item_44 Item_45 Item_46
#> [1,] 0 NA NA NA NA 1 0 NA 0
#> [2,] NA NA NA 1 NA 1 1 1 1
#> [3,] 1 NA NA NA 1 0 1 NA NA
#> [4,] 0 1 NA NA NA NA 1 1 0
#> [5,] NA 1 1 NA NA 1 NA NA 1
#> [6,] 1 NA NA NA NA 1 NA NA 1
#> Item_47 Item_48 Item_49 Item_50
#> [1,] NA NA 0 NA
#> [2,] NA 1 NA NA
#> [3,] 0 0 1 1
#> [4,] NA 1 0 1
#> [5,] NA 1 1 1
#> [6,] 0 1 NA 1
# check that all individuals had 30 items
all(rowSums(!is.na(dataset2)) == 30)
#> [1] TRUE
# Multiple Prior Weights Updating and Multiple EM Cycles (MWU-MEM)
MWU_MEM <- fixedCalib(dataset2, model = 1, old_mod = mod)
coef(MWU_MEM, simplify=TRUE)
#> $items
#> a1 d g u
#> Item_1 1.196 -0.366 0 1
#> Item_2 1.218 1.345 0 1
#> Item_3 1.029 -0.017 0 1
#> Item_4 0.817 0.230 0 1
#> Item_5 1.148 -0.462 0 1
#> Item_6 0.473 0.157 0 1
#> Item_7 1.172 0.491 0 1
#> Item_8 0.882 0.599 0 1
#> Item_9 0.732 1.367 0 1
#> Item_10 0.737 -1.703 0 1
#> Item_11 0.988 0.057 0 1
#> Item_12 1.621 -0.888 0 1
#> Item_13 1.211 0.362 0 1
#> Item_14 1.261 1.101 0 1
#> Item_15 0.748 -0.319 0 1
#> Item_16 1.171 -1.247 0 1
#> Item_17 0.742 0.637 0 1
#> Item_18 0.925 1.128 0 1
#> Item_19 1.477 0.395 0 1
#> Item_20 1.037 -0.993 0 1
#> Item_21 1.136 0.068 0 1
#> Item_22 1.402 -0.513 0 1
#> Item_23 0.679 -0.684 0 1
#> Item_24 0.483 1.690 0 1
#> Item_25 0.501 1.048 0 1
#> Item_26 1.604 0.636 0 1
#> Item_27 0.833 0.559 0 1
#> Item_28 1.100 -0.493 0 1
#> Item_29 1.200 0.354 0 1
#> Item_30 1.074 1.010 0 1
#> Item_31 1.416 0.729 0 1
#> Item_32 2.098 0.853 0 1
#> Item_33 1.622 0.025 0 1
#> Item_34 1.242 1.731 0 1
#> Item_35 1.127 0.868 0 1
#> Item_36 1.212 1.155 0 1
#> Item_37 1.022 0.621 0 1
#> Item_38 0.654 -0.203 0 1
#> Item_39 1.333 0.685 0 1
#> Item_40 0.939 0.678 0 1
#> Item_41 1.833 -0.565 0 1
#> Item_42 0.387 -0.631 0 1
#> Item_43 0.691 1.108 0 1
#> Item_44 1.232 -0.054 0 1
#> Item_45 1.105 -0.460 0 1
#> Item_46 1.401 0.694 0 1
#> Item_47 0.532 -0.290 0 1
#> Item_48 1.122 1.509 0 1
#> Item_49 1.158 -0.318 0 1
#> Item_50 0.692 -0.432 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
data.frame(coef(MWU_MEM, simplify=TRUE)$items[,c('a1','d')],
pop_a1=a, pop_d=d)
#> a1 d pop_a1 pop_d
#> Item_1 1.1961890 -0.36582599 1.1756586 -0.37827025
#> Item_2 1.2180200 1.34513036 1.2128398 1.36338487
#> Item_3 1.0287076 -0.01749165 0.9672090 0.03751319
#> Item_4 0.8169838 0.22955350 0.8639508 0.24616399
#> Item_5 1.1477420 -0.46213650 1.1817662 -0.46968358
#> Item_6 0.4734409 0.15748181 0.4546132 0.19456759
#> Item_7 1.1723767 0.49084966 1.1890296 0.48381989
#> Item_8 0.8823964 0.59861143 0.9171448 0.57665673
#> Item_9 0.7320060 1.36669674 0.9147521 1.50154551
#> Item_10 0.7374958 -1.70288028 0.7242034 -1.64286078
#> Item_11 0.9877230 0.05684034 0.9651257 0.10471439
#> Item_12 1.6208445 -0.88830542 1.5451936 -0.93977204
#> Item_13 1.2113938 0.36247319 1.1111884 0.38731215
#> Item_14 1.2608594 1.10068854 1.1560649 1.11297399
#> Item_15 0.7483149 -0.31912299 0.7748404 -0.41081572
#> Item_16 1.1708992 -1.24683338 1.2450700 -1.28266411
#> Item_17 0.7422645 0.63674114 0.7340927 0.62169760
#> Item_18 0.9248296 1.12848731 0.9005267 1.11544193
#> Item_19 1.4767582 0.39539515 1.3362138 0.36179827
#> Item_20 1.0368814 -0.99330414 1.0896171 -0.90697018
#> Item_21 1.1357543 0.06752098 1.2338866 0.03823090
#> Item_22 1.4021119 -0.51282038 1.4367355 -0.54925456
#> Item_23 0.6786602 -0.68438097 0.8067015 -0.73454697
#> Item_24 0.4828002 1.68992778 0.5340588 1.63135837
#> Item_25 0.5011412 1.04812815 0.5206871 0.98189377
#> Item_26 1.6039924 0.63625385 1.5415293 0.65982060
#> Item_27 0.8328685 0.55938549 0.8555058 0.57838080
#> Item_28 1.1001393 -0.49299690 1.1861139 -0.56807834
#> Item_29 1.1996287 0.35417420 1.1836370 0.33337380
#> Item_30 1.0736650 1.01026900 0.9513067 0.71488089
#> Item_31 1.4162584 0.72856155 1.2435620 0.45176815
#> Item_32 2.0975461 0.85255109 1.6590501 0.73020049
#> Item_33 1.6216973 0.02486148 1.6147571 -0.21305838
#> Item_34 1.2421629 1.73077613 1.4897337 1.73397764
#> Item_35 1.1268922 0.86756137 1.0762814 0.67985447
#> Item_36 1.2121379 1.15479360 1.1473565 1.30696943
#> Item_37 1.0218142 0.62136695 0.9027740 0.47042973
#> Item_38 0.6544987 -0.20307537 0.5013849 -0.21556737
#> Item_39 1.3326681 0.68465299 1.5303202 0.37556660
#> Item_40 0.9387813 0.67776738 1.0077403 0.57740905
#> Item_41 1.8326249 -0.56461189 1.3385533 -0.67473104
#> Item_42 0.3866839 -0.63085106 0.2858926 -0.59855776
#> Item_43 0.6911816 1.10845312 0.6819203 1.32086286
#> Item_44 1.2321139 -0.05383912 1.2811422 -0.27427356
#> Item_45 1.1045328 -0.45957575 1.2563355 -0.68644306
#> Item_46 1.4012118 0.69353524 1.4382188 0.48113247
#> Item_47 0.5324164 -0.28980316 0.5760704 -0.35353046
#> Item_48 1.1215187 1.50886830 1.1702210 1.51040387
#> Item_49 1.1583841 -0.31781501 1.1749563 -0.41985829
#> Item_50 0.6916807 -0.43180765 0.6079603 -0.48618269
plot(MWU_MEM, type = 'empiricalhist')
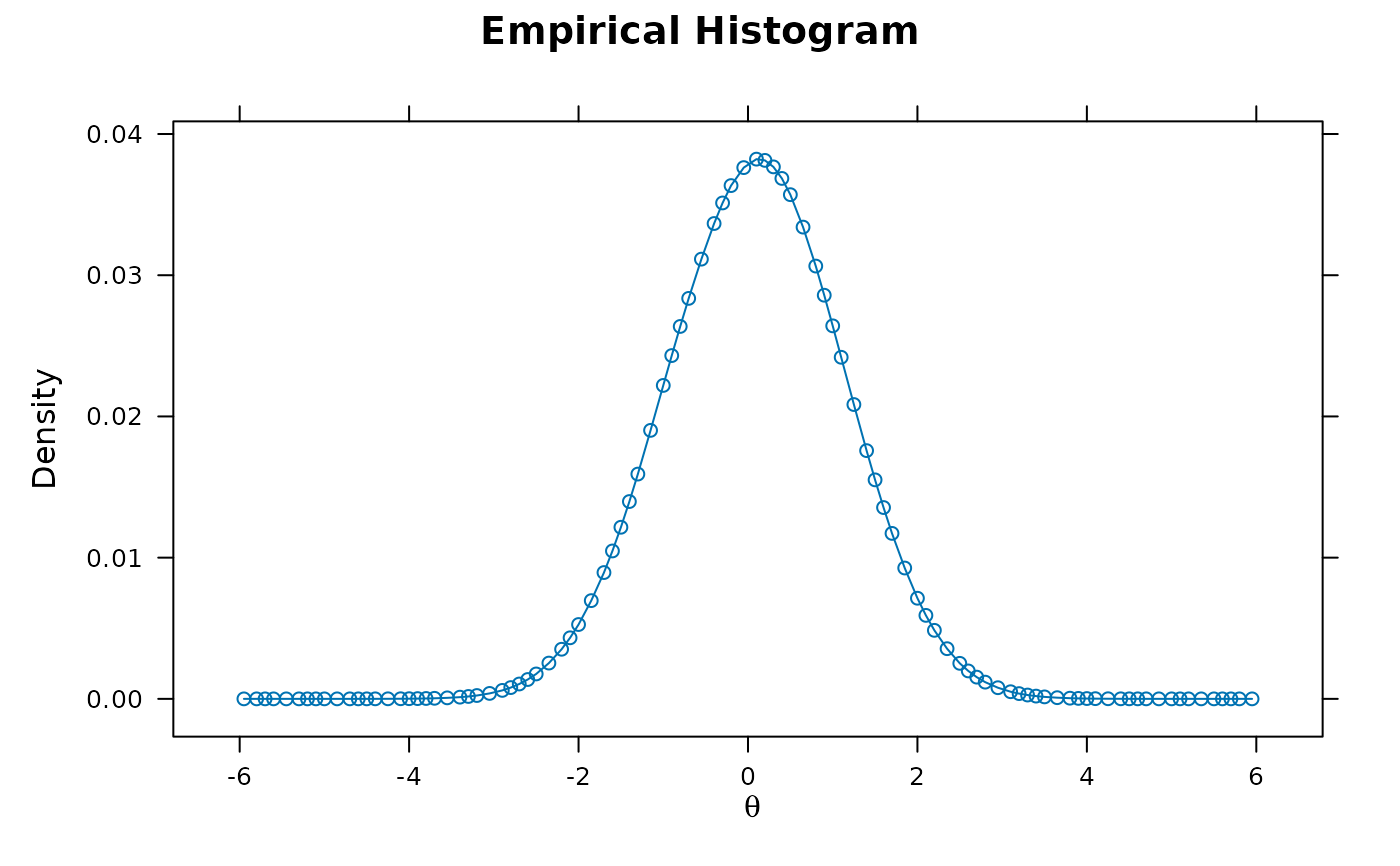 ## factor scores check
fs <- fscores(MWU_MEM)
hist(fs)
## factor scores check
fs <- fscores(MWU_MEM)
hist(fs)
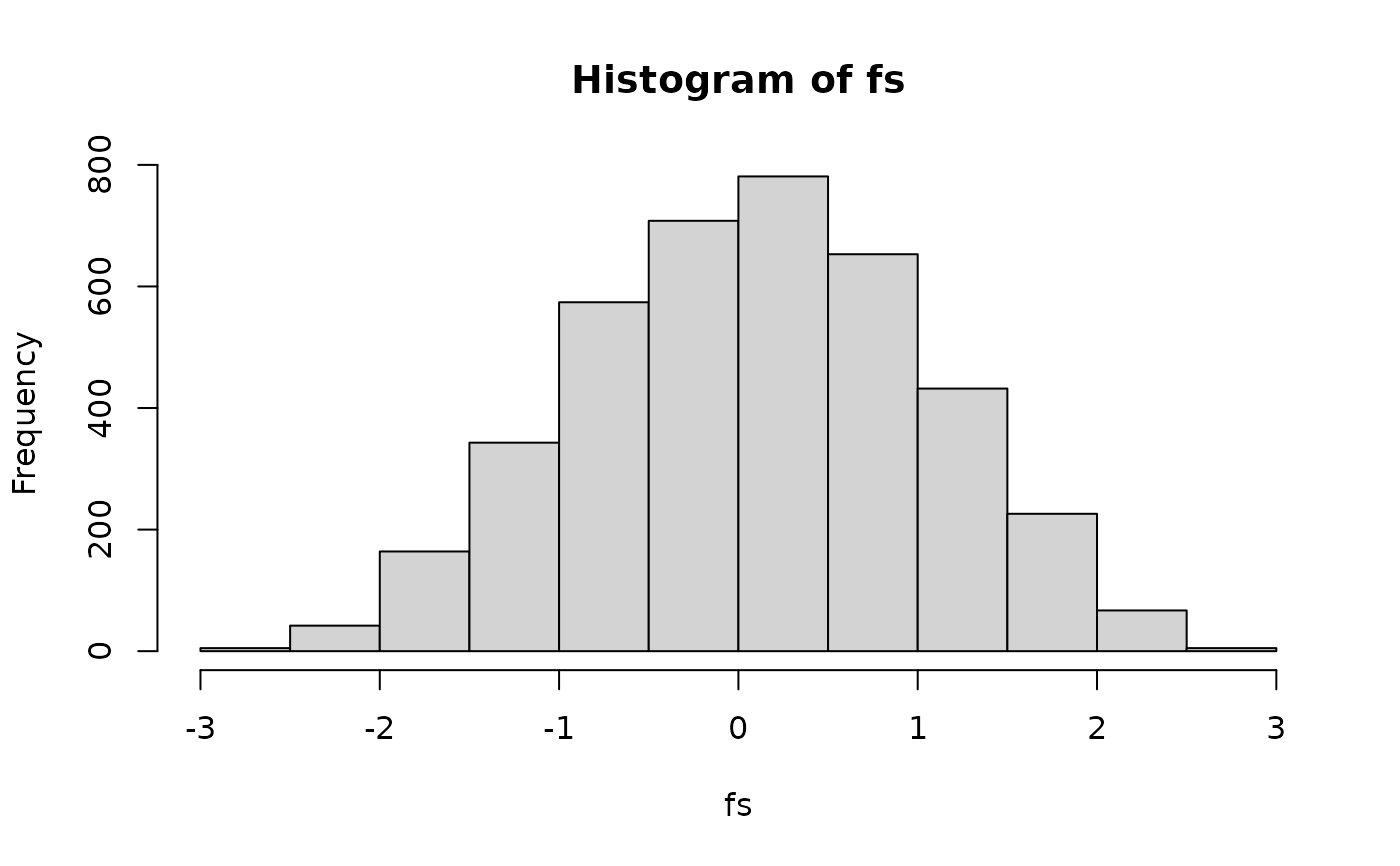 c(mean_calib=mean(fs[1:N, ]), sd_calib=sd(fs[1:N, ]))
#> mean_calib sd_calib
#> -0.0001434688 0.9215504578
## shrinkage, but generally different from calibrated sample
c(mean_exper=mean(fs[-c(1:N), ]), sd_exper=sd(fs[-c(1:N), ]))
#> mean_exper sd_exper
#> 0.3531216 1.0349737
# }
c(mean_calib=mean(fs[1:N, ]), sd_calib=sd(fs[1:N, ]))
#> mean_calib sd_calib
#> -0.0001434688 0.9215504578
## shrinkage, but generally different from calibrated sample
c(mean_exper=mean(fs[-c(1:N), ]), sd_exper=sd(fs[-c(1:N), ]))
#> mean_exper sd_exper
#> 0.3531216 1.0349737
# }