Skip to contents

Displays item surface and information plots

Source: R/itemplot.R
itemplot.Rd

itemplot displays various item based IRT plots, with special options for plotting items that contain several 0 slope parameters. Supports up to three dimensional models.

Usage

itemplot(
  object,
  item,
  type = "trace",
  degrees = 45,
  CE = FALSE,
  CEalpha = 0.05,
  CEdraws = 1000,
  drop.zeros = FALSE,
  theta_lim = c(-6, 6),
  shiny = FALSE,
  rot = list(xaxis = -70, yaxis = 30, zaxis = 10),
  par.strip.text = list(cex = 0.7),
  npts = 200,
  par.settings = list(strip.background = list(col = "#9ECAE1"), strip.border = list(col =
    "black")),
  auto.key = list(space = "right", points = FALSE, lines = TRUE),
  ...
)

Arguments

object

a computed model object of class SingleGroupClass or MultipleGroupClass. Input may also be a list for comparing similar item types (e.g., 1PL vs 2PL)

item

a single numeric value, or the item name, indicating which item to plot

type

plot type to use, information ('info'), standard errors ('SE'), item trace lines ('trace'), cumulative probability plots to indicate thresholds ('threshold'), information and standard errors ('infoSE') or information and trace lines ('infotrace'), category and total information ('infocat'), relative efficiency lines ('RE'), expected score 'score', or information and trace line contours ('infocontour' and 'tracecontour'; not supported for MultipleGroupClass objects)

degrees

the degrees argument to be used if there are two or three factors. See iteminfo for more detail. A new vector will be required for three dimensional models to override the default

CE

logical; plot confidence envelope?

CEalpha

area remaining in the tail for confidence envelope. Default gives 95% confidence region

CEdraws

draws number of draws to use for confidence envelope

drop.zeros

logical; drop slope values that are numerically close to zero to reduce dimensionality? Useful in objects returned from bfactor or other confirmatory models that contain several zero slopes

theta_lim

lower and upper limits of the latent trait (theta) to be evaluated, and is used in conjunction with npts. Default uses c(-6,6)

shiny

logical; run interactive display for item plots using the shiny interface. This primarily is an instructive tool for demonstrating how item response curves behave when adjusting their parameters

rot

a list of rotation coordinates to be used for 3 dimensional plots

par.strip.text

plotting argument passed to lattice

npts

number of quadrature points to be used for plotting features. Larger values make plots look smoother

par.settings

plotting argument passed to lattice

auto.key

plotting argument passed to lattice

...

additional arguments to be passed to lattice and coef()

References

Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06

Author

Phil Chalmers rphilip.chalmers@gmail.com

Examples

# \donttest{

data(LSAT7)
fulldata <- expand.table(LSAT7)
mod1 <- mirt(fulldata,1,SE=TRUE)
#> 
Iteration: 1, Log-Lik: -2668.786, Max-Change: 0.18243
Iteration: 2, Log-Lik: -2663.691, Max-Change: 0.13637
Iteration: 3, Log-Lik: -2661.454, Max-Change: 0.10231
Iteration: 4, Log-Lik: -2659.430, Max-Change: 0.04181
Iteration: 5, Log-Lik: -2659.241, Max-Change: 0.03417
Iteration: 6, Log-Lik: -2659.113, Max-Change: 0.02911
Iteration: 7, Log-Lik: -2658.812, Max-Change: 0.00456
Iteration: 8, Log-Lik: -2658.809, Max-Change: 0.00363
Iteration: 9, Log-Lik: -2658.808, Max-Change: 0.00273
Iteration: 10, Log-Lik: -2658.806, Max-Change: 0.00144
Iteration: 11, Log-Lik: -2658.806, Max-Change: 0.00118
Iteration: 12, Log-Lik: -2658.806, Max-Change: 0.00101
Iteration: 13, Log-Lik: -2658.805, Max-Change: 0.00042
Iteration: 14, Log-Lik: -2658.805, Max-Change: 0.00025
Iteration: 15, Log-Lik: -2658.805, Max-Change: 0.00026
Iteration: 16, Log-Lik: -2658.805, Max-Change: 0.00023
Iteration: 17, Log-Lik: -2658.805, Max-Change: 0.00023
Iteration: 18, Log-Lik: -2658.805, Max-Change: 0.00021
Iteration: 19, Log-Lik: -2658.805, Max-Change: 0.00019
Iteration: 20, Log-Lik: -2658.805, Max-Change: 0.00017
Iteration: 21, Log-Lik: -2658.805, Max-Change: 0.00017
Iteration: 22, Log-Lik: -2658.805, Max-Change: 0.00015
Iteration: 23, Log-Lik: -2658.805, Max-Change: 0.00015
Iteration: 24, Log-Lik: -2658.805, Max-Change: 0.00013
Iteration: 25, Log-Lik: -2658.805, Max-Change: 0.00013
Iteration: 26, Log-Lik: -2658.805, Max-Change: 0.00011
Iteration: 27, Log-Lik: -2658.805, Max-Change: 0.00011
Iteration: 28, Log-Lik: -2658.805, Max-Change: 0.00010
#> 
#> Calculating information matrix...
mod2 <- mirt(fulldata,1, itemtype = 'Rasch')
#> 
Iteration: 1, Log-Lik: -2664.942, Max-Change: 0.01075
Iteration: 2, Log-Lik: -2664.913, Max-Change: 0.00257
Iteration: 3, Log-Lik: -2664.910, Max-Change: 0.00210
Iteration: 4, Log-Lik: -2664.908, Max-Change: 0.00179
Iteration: 5, Log-Lik: -2664.906, Max-Change: 0.00156
Iteration: 6, Log-Lik: -2664.905, Max-Change: 0.00137
Iteration: 7, Log-Lik: -2664.904, Max-Change: 0.00141
Iteration: 8, Log-Lik: -2664.903, Max-Change: 0.00110
Iteration: 9, Log-Lik: -2664.903, Max-Change: 0.00095
Iteration: 10, Log-Lik: -2664.902, Max-Change: 0.00086
Iteration: 11, Log-Lik: -2664.902, Max-Change: 0.00072
Iteration: 12, Log-Lik: -2664.902, Max-Change: 0.00063
Iteration: 13, Log-Lik: -2664.902, Max-Change: 0.00065
Iteration: 14, Log-Lik: -2664.901, Max-Change: 0.00051
Iteration: 15, Log-Lik: -2664.901, Max-Change: 0.00044
Iteration: 16, Log-Lik: -2664.901, Max-Change: 0.00040
Iteration: 17, Log-Lik: -2664.901, Max-Change: 0.00034
Iteration: 18, Log-Lik: -2664.901, Max-Change: 0.00029
Iteration: 19, Log-Lik: -2664.901, Max-Change: 0.00030
Iteration: 20, Log-Lik: -2664.901, Max-Change: 0.00024
Iteration: 21, Log-Lik: -2664.901, Max-Change: 0.00020
Iteration: 22, Log-Lik: -2664.901, Max-Change: 0.00018
Iteration: 23, Log-Lik: -2664.901, Max-Change: 0.00016
Iteration: 24, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 25, Log-Lik: -2664.901, Max-Change: 0.00014
Iteration: 26, Log-Lik: -2664.901, Max-Change: 0.00011
Iteration: 27, Log-Lik: -2664.901, Max-Change: 0.00009
mod3 <- mirt(fulldata,2)
#> 
Iteration: 1, Log-Lik: -2674.021, Max-Change: 0.20368
Iteration: 2, Log-Lik: -2658.770, Max-Change: 0.12215
Iteration: 3, Log-Lik: -2655.896, Max-Change: 0.07195
Iteration: 4, Log-Lik: -2654.819, Max-Change: 0.03372
Iteration: 5, Log-Lik: -2654.630, Max-Change: 0.02022
Iteration: 6, Log-Lik: -2654.553, Max-Change: 0.01189
Iteration: 7, Log-Lik: -2654.493, Max-Change: 0.00789
Iteration: 8, Log-Lik: -2654.475, Max-Change: 0.00763
Iteration: 9, Log-Lik: -2654.460, Max-Change: 0.00744
Iteration: 10, Log-Lik: -2654.379, Max-Change: 0.00615
Iteration: 11, Log-Lik: -2654.368, Max-Change: 0.00600
Iteration: 12, Log-Lik: -2654.357, Max-Change: 0.00589
Iteration: 13, Log-Lik: -2654.297, Max-Change: 0.00550
Iteration: 14, Log-Lik: -2654.288, Max-Change: 0.00545
Iteration: 15, Log-Lik: -2654.280, Max-Change: 0.00540
Iteration: 16, Log-Lik: -2654.232, Max-Change: 0.00523
Iteration: 17, Log-Lik: -2654.224, Max-Change: 0.00515
Iteration: 18, Log-Lik: -2654.218, Max-Change: 0.00509
Iteration: 19, Log-Lik: -2654.179, Max-Change: 0.00497
Iteration: 20, Log-Lik: -2654.173, Max-Change: 0.00492
Iteration: 21, Log-Lik: -2654.167, Max-Change: 0.00487
Iteration: 22, Log-Lik: -2654.134, Max-Change: 0.00466
Iteration: 23, Log-Lik: -2654.130, Max-Change: 0.00460
Iteration: 24, Log-Lik: -2654.125, Max-Change: 0.00455
Iteration: 25, Log-Lik: -2654.097, Max-Change: 0.00437
Iteration: 26, Log-Lik: -2654.093, Max-Change: 0.00434
Iteration: 27, Log-Lik: -2654.089, Max-Change: 0.00431
Iteration: 28, Log-Lik: -2654.066, Max-Change: 0.00420
Iteration: 29, Log-Lik: -2654.062, Max-Change: 0.00416
Iteration: 30, Log-Lik: -2654.058, Max-Change: 0.00413
Iteration: 31, Log-Lik: -2654.038, Max-Change: 0.00404
Iteration: 32, Log-Lik: -2654.034, Max-Change: 0.00401
Iteration: 33, Log-Lik: -2654.031, Max-Change: 0.00399
Iteration: 34, Log-Lik: -2654.012, Max-Change: 0.00391
Iteration: 35, Log-Lik: -2654.009, Max-Change: 0.00389
Iteration: 36, Log-Lik: -2654.006, Max-Change: 0.00387
Iteration: 37, Log-Lik: -2653.989, Max-Change: 0.00373
Iteration: 38, Log-Lik: -2653.986, Max-Change: 0.00372
Iteration: 39, Log-Lik: -2653.983, Max-Change: 0.00370
Iteration: 40, Log-Lik: -2653.966, Max-Change: 0.00366
Iteration: 41, Log-Lik: -2653.964, Max-Change: 0.00363
Iteration: 42, Log-Lik: -2653.961, Max-Change: 0.00362
Iteration: 43, Log-Lik: -2653.945, Max-Change: 0.00355
Iteration: 44, Log-Lik: -2653.943, Max-Change: 0.00353
Iteration: 45, Log-Lik: -2653.940, Max-Change: 0.00352
Iteration: 46, Log-Lik: -2653.925, Max-Change: 0.00347
Iteration: 47, Log-Lik: -2653.922, Max-Change: 0.00345
Iteration: 48, Log-Lik: -2653.920, Max-Change: 0.00344
Iteration: 49, Log-Lik: -2653.905, Max-Change: 0.00340
Iteration: 50, Log-Lik: -2653.902, Max-Change: 0.00339
Iteration: 51, Log-Lik: -2653.900, Max-Change: 0.00338
Iteration: 52, Log-Lik: -2653.884, Max-Change: 0.00335
Iteration: 53, Log-Lik: -2653.882, Max-Change: 0.00334
Iteration: 54, Log-Lik: -2653.879, Max-Change: 0.00333
Iteration: 55, Log-Lik: -2653.864, Max-Change: 0.00331
Iteration: 56, Log-Lik: -2653.862, Max-Change: 0.00330
Iteration: 57, Log-Lik: -2653.859, Max-Change: 0.00329
Iteration: 58, Log-Lik: -2653.844, Max-Change: 0.00326
Iteration: 59, Log-Lik: -2653.842, Max-Change: 0.00325
Iteration: 60, Log-Lik: -2653.839, Max-Change: 0.00324
Iteration: 61, Log-Lik: -2653.824, Max-Change: 0.00321
Iteration: 62, Log-Lik: -2653.822, Max-Change: 0.00320
Iteration: 63, Log-Lik: -2653.819, Max-Change: 0.00319
Iteration: 64, Log-Lik: -2653.804, Max-Change: 0.00315
Iteration: 65, Log-Lik: -2653.802, Max-Change: 0.00315
Iteration: 66, Log-Lik: -2653.800, Max-Change: 0.00314
Iteration: 67, Log-Lik: -2653.785, Max-Change: 0.00309
Iteration: 68, Log-Lik: -2653.783, Max-Change: 0.00309
Iteration: 69, Log-Lik: -2653.780, Max-Change: 0.00308
Iteration: 70, Log-Lik: -2653.766, Max-Change: 0.00303
Iteration: 71, Log-Lik: -2653.764, Max-Change: 0.00302
Iteration: 72, Log-Lik: -2653.762, Max-Change: 0.00301
Iteration: 73, Log-Lik: -2653.748, Max-Change: 0.00295
Iteration: 74, Log-Lik: -2653.746, Max-Change: 0.00294
Iteration: 75, Log-Lik: -2653.743, Max-Change: 0.00293
Iteration: 76, Log-Lik: -2653.730, Max-Change: 0.00287
Iteration: 77, Log-Lik: -2653.728, Max-Change: 0.00286
Iteration: 78, Log-Lik: -2653.726, Max-Change: 0.00285
Iteration: 79, Log-Lik: -2653.713, Max-Change: 0.00281
Iteration: 80, Log-Lik: -2653.711, Max-Change: 0.00281
Iteration: 81, Log-Lik: -2653.709, Max-Change: 0.00281
Iteration: 82, Log-Lik: -2653.698, Max-Change: 0.00283
Iteration: 83, Log-Lik: -2653.696, Max-Change: 0.00282
Iteration: 84, Log-Lik: -2653.694, Max-Change: 0.00282
Iteration: 85, Log-Lik: -2653.683, Max-Change: 0.00282
Iteration: 86, Log-Lik: -2653.681, Max-Change: 0.00282
Iteration: 87, Log-Lik: -2653.679, Max-Change: 0.00281
Iteration: 88, Log-Lik: -2653.669, Max-Change: 0.00281
Iteration: 89, Log-Lik: -2653.667, Max-Change: 0.00280
Iteration: 90, Log-Lik: -2653.665, Max-Change: 0.00279
Iteration: 91, Log-Lik: -2653.655, Max-Change: 0.00278
Iteration: 92, Log-Lik: -2653.654, Max-Change: 0.00277
Iteration: 93, Log-Lik: -2653.652, Max-Change: 0.00276
Iteration: 94, Log-Lik: -2653.643, Max-Change: 0.00274
Iteration: 95, Log-Lik: -2653.642, Max-Change: 0.00273
Iteration: 96, Log-Lik: -2653.640, Max-Change: 0.00272
Iteration: 97, Log-Lik: -2653.632, Max-Change: 0.00269
Iteration: 98, Log-Lik: -2653.631, Max-Change: 0.00268
Iteration: 99, Log-Lik: -2653.630, Max-Change: 0.00267
Iteration: 100, Log-Lik: -2653.622, Max-Change: 0.00263
Iteration: 101, Log-Lik: -2653.621, Max-Change: 0.00262
Iteration: 102, Log-Lik: -2653.619, Max-Change: 0.00261
Iteration: 103, Log-Lik: -2653.612, Max-Change: 0.00256
Iteration: 104, Log-Lik: -2653.611, Max-Change: 0.00255
Iteration: 105, Log-Lik: -2653.610, Max-Change: 0.00254
Iteration: 106, Log-Lik: -2653.604, Max-Change: 0.00249
Iteration: 107, Log-Lik: -2653.603, Max-Change: 0.00248
Iteration: 108, Log-Lik: -2653.602, Max-Change: 0.00247
Iteration: 109, Log-Lik: -2653.596, Max-Change: 0.00242
Iteration: 110, Log-Lik: -2653.595, Max-Change: 0.00241
Iteration: 111, Log-Lik: -2653.594, Max-Change: 0.00239
Iteration: 112, Log-Lik: -2653.589, Max-Change: 0.00234
Iteration: 113, Log-Lik: -2653.588, Max-Change: 0.00233
Iteration: 114, Log-Lik: -2653.587, Max-Change: 0.00232
Iteration: 115, Log-Lik: -2653.582, Max-Change: 0.00226
Iteration: 116, Log-Lik: -2653.581, Max-Change: 0.00225
Iteration: 117, Log-Lik: -2653.580, Max-Change: 0.00224
Iteration: 118, Log-Lik: -2653.576, Max-Change: 0.00218
Iteration: 119, Log-Lik: -2653.575, Max-Change: 0.00217
Iteration: 120, Log-Lik: -2653.575, Max-Change: 0.00216
Iteration: 121, Log-Lik: -2653.571, Max-Change: 0.00210
Iteration: 122, Log-Lik: -2653.570, Max-Change: 0.00209
Iteration: 123, Log-Lik: -2653.569, Max-Change: 0.00208
Iteration: 124, Log-Lik: -2653.566, Max-Change: 0.00202
Iteration: 125, Log-Lik: -2653.565, Max-Change: 0.00201
Iteration: 126, Log-Lik: -2653.565, Max-Change: 0.00200
Iteration: 127, Log-Lik: -2653.561, Max-Change: 0.00194
Iteration: 128, Log-Lik: -2653.561, Max-Change: 0.00193
Iteration: 129, Log-Lik: -2653.560, Max-Change: 0.00192
Iteration: 130, Log-Lik: -2653.557, Max-Change: 0.00186
Iteration: 131, Log-Lik: -2653.557, Max-Change: 0.00185
Iteration: 132, Log-Lik: -2653.556, Max-Change: 0.00184
Iteration: 133, Log-Lik: -2653.554, Max-Change: 0.00179
Iteration: 134, Log-Lik: -2653.553, Max-Change: 0.00178
Iteration: 135, Log-Lik: -2653.553, Max-Change: 0.00177
Iteration: 136, Log-Lik: -2653.550, Max-Change: 0.00171
Iteration: 137, Log-Lik: -2653.550, Max-Change: 0.00170
Iteration: 138, Log-Lik: -2653.550, Max-Change: 0.00169
Iteration: 139, Log-Lik: -2653.547, Max-Change: 0.00164
Iteration: 140, Log-Lik: -2653.547, Max-Change: 0.00163
Iteration: 141, Log-Lik: -2653.547, Max-Change: 0.00162
Iteration: 142, Log-Lik: -2653.545, Max-Change: 0.00157
Iteration: 143, Log-Lik: -2653.544, Max-Change: 0.00148
Iteration: 144, Log-Lik: -2653.544, Max-Change: 0.00148
Iteration: 145, Log-Lik: -2653.543, Max-Change: 0.00196
Iteration: 146, Log-Lik: -2653.543, Max-Change: 0.00138
Iteration: 147, Log-Lik: -2653.542, Max-Change: 0.00137
Iteration: 148, Log-Lik: -2653.541, Max-Change: 0.00143
Iteration: 149, Log-Lik: -2653.541, Max-Change: 0.00137
Iteration: 150, Log-Lik: -2653.541, Max-Change: 0.00138
Iteration: 151, Log-Lik: -2653.539, Max-Change: 0.00134
Iteration: 152, Log-Lik: -2653.539, Max-Change: 0.00137
Iteration: 153, Log-Lik: -2653.539, Max-Change: 0.00131
Iteration: 154, Log-Lik: -2653.538, Max-Change: 0.00113
Iteration: 155, Log-Lik: -2653.538, Max-Change: 0.00130
Iteration: 156, Log-Lik: -2653.537, Max-Change: 0.00130
Iteration: 157, Log-Lik: -2653.537, Max-Change: 0.00121
Iteration: 158, Log-Lik: -2653.536, Max-Change: 0.00109
Iteration: 159, Log-Lik: -2653.536, Max-Change: 0.00126
Iteration: 160, Log-Lik: -2653.536, Max-Change: 0.00102
Iteration: 161, Log-Lik: -2653.536, Max-Change: 0.00119
Iteration: 162, Log-Lik: -2653.535, Max-Change: 0.00096
Iteration: 163, Log-Lik: -2653.535, Max-Change: 0.00213
Iteration: 164, Log-Lik: -2653.535, Max-Change: 0.00194
Iteration: 165, Log-Lik: -2653.534, Max-Change: 0.00196
Iteration: 166, Log-Lik: -2653.533, Max-Change: 0.00105
Iteration: 167, Log-Lik: -2653.532, Max-Change: 0.00118
Iteration: 168, Log-Lik: -2653.532, Max-Change: 0.00111
Iteration: 169, Log-Lik: -2653.532, Max-Change: 0.00094
Iteration: 170, Log-Lik: -2653.531, Max-Change: 0.00093
Iteration: 171, Log-Lik: -2653.531, Max-Change: 0.00093
Iteration: 172, Log-Lik: -2653.531, Max-Change: 0.00165
Iteration: 173, Log-Lik: -2653.530, Max-Change: 0.00157
Iteration: 174, Log-Lik: -2653.530, Max-Change: 0.00181
Iteration: 175, Log-Lik: -2653.530, Max-Change: 0.00098
Iteration: 176, Log-Lik: -2653.529, Max-Change: 0.00161
Iteration: 177, Log-Lik: -2653.529, Max-Change: 0.00163
Iteration: 178, Log-Lik: -2653.529, Max-Change: 0.00106
Iteration: 179, Log-Lik: -2653.529, Max-Change: 0.00074
Iteration: 180, Log-Lik: -2653.528, Max-Change: 0.00177
Iteration: 181, Log-Lik: -2653.528, Max-Change: 0.00143
Iteration: 182, Log-Lik: -2653.528, Max-Change: 0.00145
Iteration: 183, Log-Lik: -2653.528, Max-Change: 0.00150
Iteration: 184, Log-Lik: -2653.527, Max-Change: 0.00088
Iteration: 185, Log-Lik: -2653.527, Max-Change: 0.00035
Iteration: 186, Log-Lik: -2653.527, Max-Change: 0.00029
Iteration: 187, Log-Lik: -2653.527, Max-Change: 0.00031
Iteration: 188, Log-Lik: -2653.527, Max-Change: 0.00032
Iteration: 189, Log-Lik: -2653.527, Max-Change: 0.00033
Iteration: 190, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 191, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 192, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 193, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 194, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 195, Log-Lik: -2653.527, Max-Change: 0.00034
Iteration: 196, Log-Lik: -2653.527, Max-Change: 0.00033
Iteration: 197, Log-Lik: -2653.527, Max-Change: 0.00033
Iteration: 198, Log-Lik: -2653.527, Max-Change: 0.00033
Iteration: 199, Log-Lik: -2653.526, Max-Change: 0.00033
Iteration: 200, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 201, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 202, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 203, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 204, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 205, Log-Lik: -2653.526, Max-Change: 0.00032
Iteration: 206, Log-Lik: -2653.526, Max-Change: 0.00031
Iteration: 207, Log-Lik: -2653.526, Max-Change: 0.00031
Iteration: 208, Log-Lik: -2653.526, Max-Change: 0.00031
Iteration: 209, Log-Lik: -2653.526, Max-Change: 0.00031
Iteration: 210, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 211, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 212, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 213, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 214, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 215, Log-Lik: -2653.526, Max-Change: 0.00030
Iteration: 216, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 217, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 218, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 219, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 220, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 221, Log-Lik: -2653.526, Max-Change: 0.00029
Iteration: 222, Log-Lik: -2653.526, Max-Change: 0.00028
Iteration: 223, Log-Lik: -2653.526, Max-Change: 0.00028
Iteration: 224, Log-Lik: -2653.526, Max-Change: 0.00028
Iteration: 225, Log-Lik: -2653.525, Max-Change: 0.00028
Iteration: 226, Log-Lik: -2653.525, Max-Change: 0.00028
Iteration: 227, Log-Lik: -2653.525, Max-Change: 0.00028
Iteration: 228, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 229, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 230, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 231, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 232, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 233, Log-Lik: -2653.525, Max-Change: 0.00027
Iteration: 234, Log-Lik: -2653.525, Max-Change: 0.00133
Iteration: 235, Log-Lik: -2653.525, Max-Change: 0.00148
Iteration: 236, Log-Lik: -2653.525, Max-Change: 0.00026
Iteration: 237, Log-Lik: -2653.525, Max-Change: 0.00023
Iteration: 238, Log-Lik: -2653.525, Max-Change: 0.00024
Iteration: 239, Log-Lik: -2653.525, Max-Change: 0.00122
Iteration: 240, Log-Lik: -2653.525, Max-Change: 0.00041
Iteration: 241, Log-Lik: -2653.525, Max-Change: 0.00026
Iteration: 242, Log-Lik: -2653.525, Max-Change: 0.00025
Iteration: 243, Log-Lik: -2653.525, Max-Change: 0.00124
Iteration: 244, Log-Lik: -2653.525, Max-Change: 0.00134
Iteration: 245, Log-Lik: -2653.524, Max-Change: 0.00033
Iteration: 246, Log-Lik: -2653.524, Max-Change: 0.00021
Iteration: 247, Log-Lik: -2653.524, Max-Change: 0.00115
Iteration: 248, Log-Lik: -2653.524, Max-Change: 0.00036
Iteration: 249, Log-Lik: -2653.524, Max-Change: 0.00024
Iteration: 250, Log-Lik: -2653.524, Max-Change: 0.00116
Iteration: 251, Log-Lik: -2653.524, Max-Change: 0.00022
Iteration: 252, Log-Lik: -2653.524, Max-Change: 0.00022
Iteration: 253, Log-Lik: -2653.524, Max-Change: 0.00022
Iteration: 254, Log-Lik: -2653.524, Max-Change: 0.00112
Iteration: 255, Log-Lik: -2653.524, Max-Change: 0.00072
Iteration: 256, Log-Lik: -2653.524, Max-Change: 0.00022
Iteration: 257, Log-Lik: -2653.524, Max-Change: 0.00022
Iteration: 258, Log-Lik: -2653.524, Max-Change: 0.00108
Iteration: 259, Log-Lik: -2653.524, Max-Change: 0.00090
Iteration: 260, Log-Lik: -2653.524, Max-Change: 0.00063
Iteration: 261, Log-Lik: -2653.524, Max-Change: 0.00043
Iteration: 262, Log-Lik: -2653.524, Max-Change: 0.00106
Iteration: 263, Log-Lik: -2653.524, Max-Change: 0.00031
Iteration: 264, Log-Lik: -2653.524, Max-Change: 0.00021
Iteration: 265, Log-Lik: -2653.524, Max-Change: 0.00103
Iteration: 266, Log-Lik: -2653.523, Max-Change: 0.00056
Iteration: 267, Log-Lik: -2653.523, Max-Change: 0.00039
Iteration: 268, Log-Lik: -2653.523, Max-Change: 0.00101
Iteration: 269, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 270, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 271, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 272, Log-Lik: -2653.523, Max-Change: 0.00099
Iteration: 273, Log-Lik: -2653.523, Max-Change: 0.00067
Iteration: 274, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 275, Log-Lik: -2653.523, Max-Change: 0.00019
Iteration: 276, Log-Lik: -2653.523, Max-Change: 0.00097
Iteration: 277, Log-Lik: -2653.523, Max-Change: 0.00084
Iteration: 278, Log-Lik: -2653.523, Max-Change: 0.00058
Iteration: 279, Log-Lik: -2653.523, Max-Change: 0.00040
Iteration: 280, Log-Lik: -2653.523, Max-Change: 0.00095
Iteration: 281, Log-Lik: -2653.523, Max-Change: 0.00028
Iteration: 282, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 283, Log-Lik: -2653.523, Max-Change: 0.00093
Iteration: 284, Log-Lik: -2653.523, Max-Change: 0.00054
Iteration: 285, Log-Lik: -2653.523, Max-Change: 0.00037
Iteration: 286, Log-Lik: -2653.523, Max-Change: 0.00092
Iteration: 287, Log-Lik: -2653.523, Max-Change: 0.00020
Iteration: 288, Log-Lik: -2653.523, Max-Change: 0.00018
Iteration: 289, Log-Lik: -2653.523, Max-Change: 0.00090
Iteration: 290, Log-Lik: -2653.523, Max-Change: 0.00078
Iteration: 291, Log-Lik: -2653.523, Max-Change: 0.00055
Iteration: 292, Log-Lik: -2653.523, Max-Change: 0.00088
Iteration: 293, Log-Lik: -2653.523, Max-Change: 0.00079
Iteration: 294, Log-Lik: -2653.523, Max-Change: 0.00055
Iteration: 295, Log-Lik: -2653.522, Max-Change: 0.00087
Iteration: 296, Log-Lik: -2653.522, Max-Change: 0.00081
Iteration: 297, Log-Lik: -2653.522, Max-Change: 0.00057
Iteration: 298, Log-Lik: -2653.522, Max-Change: 0.00017
Iteration: 299, Log-Lik: -2653.522, Max-Change: 0.00086
Iteration: 300, Log-Lik: -2653.522, Max-Change: 0.00061
Iteration: 301, Log-Lik: -2653.522, Max-Change: 0.00017
Iteration: 302, Log-Lik: -2653.522, Max-Change: 0.00017
Iteration: 303, Log-Lik: -2653.522, Max-Change: 0.00084
Iteration: 304, Log-Lik: -2653.522, Max-Change: 0.00075
Iteration: 305, Log-Lik: -2653.522, Max-Change: 0.00052
Iteration: 306, Log-Lik: -2653.522, Max-Change: 0.00036
Iteration: 307, Log-Lik: -2653.522, Max-Change: 0.00083
Iteration: 308, Log-Lik: -2653.522, Max-Change: 0.00026
Iteration: 309, Log-Lik: -2653.522, Max-Change: 0.00017
Iteration: 310, Log-Lik: -2653.522, Max-Change: 0.00081
Iteration: 311, Log-Lik: -2653.522, Max-Change: 0.00049
Iteration: 312, Log-Lik: -2653.522, Max-Change: 0.00034
Iteration: 313, Log-Lik: -2653.522, Max-Change: 0.00080
Iteration: 314, Log-Lik: -2653.522, Max-Change: 0.00020
Iteration: 315, Log-Lik: -2653.522, Max-Change: 0.00016
Iteration: 316, Log-Lik: -2653.522, Max-Change: 0.00079
Iteration: 317, Log-Lik: -2653.522, Max-Change: 0.00065
Iteration: 318, Log-Lik: -2653.522, Max-Change: 0.00045
Iteration: 319, Log-Lik: -2653.522, Max-Change: 0.00078
Iteration: 320, Log-Lik: -2653.522, Max-Change: 0.00059
Iteration: 321, Log-Lik: -2653.522, Max-Change: 0.00041
Iteration: 322, Log-Lik: -2653.522, Max-Change: 0.00077
Iteration: 323, Log-Lik: -2653.522, Max-Change: 0.00047
Iteration: 324, Log-Lik: -2653.522, Max-Change: 0.00033
Iteration: 325, Log-Lik: -2653.522, Max-Change: 0.00076
Iteration: 326, Log-Lik: -2653.522, Max-Change: 0.00021
Iteration: 327, Log-Lik: -2653.522, Max-Change: 0.00015
Iteration: 328, Log-Lik: -2653.522, Max-Change: 0.00074
Iteration: 329, Log-Lik: -2653.522, Max-Change: 0.00056
Iteration: 330, Log-Lik: -2653.522, Max-Change: 0.00039
Iteration: 331, Log-Lik: -2653.522, Max-Change: 0.00074
Iteration: 332, Log-Lik: -2653.521, Max-Change: 0.00043
Iteration: 333, Log-Lik: -2653.521, Max-Change: 0.00030
Iteration: 334, Log-Lik: -2653.521, Max-Change: 0.00073
Iteration: 335, Log-Lik: -2653.521, Max-Change: 0.00015
Iteration: 336, Log-Lik: -2653.521, Max-Change: 0.00072
Iteration: 337, Log-Lik: -2653.521, Max-Change: 0.00086
Iteration: 338, Log-Lik: -2653.521, Max-Change: 0.00060
Iteration: 339, Log-Lik: -2653.521, Max-Change: 0.00041
Iteration: 340, Log-Lik: -2653.521, Max-Change: 0.00071
Iteration: 341, Log-Lik: -2653.521, Max-Change: 0.00054
Iteration: 342, Log-Lik: -2653.521, Max-Change: 0.00037
Iteration: 343, Log-Lik: -2653.521, Max-Change: 0.00070
Iteration: 344, Log-Lik: -2653.521, Max-Change: 0.00042
Iteration: 345, Log-Lik: -2653.521, Max-Change: 0.00029
Iteration: 346, Log-Lik: -2653.521, Max-Change: 0.00069
Iteration: 347, Log-Lik: -2653.521, Max-Change: 0.00014
Iteration: 348, Log-Lik: -2653.521, Max-Change: 0.00014
Iteration: 349, Log-Lik: -2653.521, Max-Change: 0.00068
Iteration: 350, Log-Lik: -2653.521, Max-Change: 0.00069
Iteration: 351, Log-Lik: -2653.521, Max-Change: 0.00048
Iteration: 352, Log-Lik: -2653.521, Max-Change: 0.00013
Iteration: 353, Log-Lik: -2653.521, Max-Change: 0.00068
Iteration: 354, Log-Lik: -2653.521, Max-Change: 0.00054
Iteration: 355, Log-Lik: -2653.521, Max-Change: 0.00014
Iteration: 356, Log-Lik: -2653.521, Max-Change: 0.00013
Iteration: 357, Log-Lik: -2653.521, Max-Change: 0.00066
Iteration: 358, Log-Lik: -2653.521, Max-Change: 0.00061
Iteration: 359, Log-Lik: -2653.521, Max-Change: 0.00042
Iteration: 360, Log-Lik: -2653.521, Max-Change: 0.00029
Iteration: 361, Log-Lik: -2653.521, Max-Change: 0.00065
Iteration: 362, Log-Lik: -2653.521, Max-Change: 0.00020
Iteration: 363, Log-Lik: -2653.521, Max-Change: 0.00014
Iteration: 364, Log-Lik: -2653.521, Max-Change: 0.00064
Iteration: 365, Log-Lik: -2653.521, Max-Change: 0.00041
Iteration: 366, Log-Lik: -2653.521, Max-Change: 0.00029
Iteration: 367, Log-Lik: -2653.521, Max-Change: 0.00064
Iteration: 368, Log-Lik: -2653.521, Max-Change: 0.00020
Iteration: 369, Log-Lik: -2653.521, Max-Change: 0.00014
Iteration: 370, Log-Lik: -2653.521, Max-Change: 0.00063
Iteration: 371, Log-Lik: -2653.521, Max-Change: 0.00041
Iteration: 372, Log-Lik: -2653.521, Max-Change: 0.00028
Iteration: 373, Log-Lik: -2653.521, Max-Change: 0.00062
Iteration: 374, Log-Lik: -2653.521, Max-Change: 0.00020
Iteration: 375, Log-Lik: -2653.521, Max-Change: 0.00013
Iteration: 376, Log-Lik: -2653.521, Max-Change: 0.00061
Iteration: 377, Log-Lik: -2653.521, Max-Change: 0.00039
Iteration: 378, Log-Lik: -2653.521, Max-Change: 0.00027
Iteration: 379, Log-Lik: -2653.521, Max-Change: 0.00061
Iteration: 380, Log-Lik: -2653.520, Max-Change: 0.00018
Iteration: 381, Log-Lik: -2653.520, Max-Change: 0.00013
Iteration: 382, Log-Lik: -2653.520, Max-Change: 0.00060
Iteration: 383, Log-Lik: -2653.520, Max-Change: 0.00042
Iteration: 384, Log-Lik: -2653.520, Max-Change: 0.00029
Iteration: 385, Log-Lik: -2653.520, Max-Change: 0.00060
Iteration: 386, Log-Lik: -2653.520, Max-Change: 0.00027
Iteration: 387, Log-Lik: -2653.520, Max-Change: 0.00019
Iteration: 388, Log-Lik: -2653.520, Max-Change: 0.00059
Iteration: 389, Log-Lik: -2653.520, Max-Change: 0.00012
Iteration: 390, Log-Lik: -2653.520, Max-Change: 0.00058
Iteration: 391, Log-Lik: -2653.520, Max-Change: 0.00069
Iteration: 392, Log-Lik: -2653.520, Max-Change: 0.00048
Iteration: 393, Log-Lik: -2653.520, Max-Change: 0.00034
Iteration: 394, Log-Lik: -2653.520, Max-Change: 0.00058
Iteration: 395, Log-Lik: -2653.520, Max-Change: 0.00043
Iteration: 396, Log-Lik: -2653.520, Max-Change: 0.00030
Iteration: 397, Log-Lik: -2653.520, Max-Change: 0.00057
Iteration: 398, Log-Lik: -2653.520, Max-Change: 0.00032
Iteration: 399, Log-Lik: -2653.520, Max-Change: 0.00022
Iteration: 400, Log-Lik: -2653.520, Max-Change: 0.00056
Iteration: 401, Log-Lik: -2653.520, Max-Change: 0.00056
Iteration: 402, Log-Lik: -2653.520, Max-Change: 0.00042
Iteration: 403, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 404, Log-Lik: -2653.520, Max-Change: 0.00055
Iteration: 405, Log-Lik: -2653.520, Max-Change: 0.00060
Iteration: 406, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 407, Log-Lik: -2653.520, Max-Change: 0.00054
Iteration: 408, Log-Lik: -2653.520, Max-Change: 0.00055
Iteration: 409, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 410, Log-Lik: -2653.520, Max-Change: 0.00054
Iteration: 411, Log-Lik: -2653.520, Max-Change: 0.00056
Iteration: 412, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 413, Log-Lik: -2653.520, Max-Change: 0.00053
Iteration: 414, Log-Lik: -2653.520, Max-Change: 0.00055
Iteration: 415, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 416, Log-Lik: -2653.520, Max-Change: 0.00053
Iteration: 417, Log-Lik: -2653.520, Max-Change: 0.00054
Iteration: 418, Log-Lik: -2653.520, Max-Change: 0.00011
Iteration: 419, Log-Lik: -2653.520, Max-Change: 0.00052
Iteration: 420, Log-Lik: -2653.520, Max-Change: 0.00054
Iteration: 421, Log-Lik: -2653.520, Max-Change: 0.00010
Iteration: 422, Log-Lik: -2653.520, Max-Change: 0.00052
Iteration: 423, Log-Lik: -2653.520, Max-Change: 0.00053
Iteration: 424, Log-Lik: -2653.520, Max-Change: 0.00010
Iteration: 425, Log-Lik: -2653.520, Max-Change: 0.00051
Iteration: 426, Log-Lik: -2653.520, Max-Change: 0.00053
Iteration: 427, Log-Lik: -2653.520, Max-Change: 0.00010
Iteration: 428, Log-Lik: -2653.520, Max-Change: 0.00050
Iteration: 429, Log-Lik: -2653.520, Max-Change: 0.00052
Iteration: 430, Log-Lik: -2653.520, Max-Change: 0.00010
Iteration: 431, Log-Lik: -2653.520, Max-Change: 0.00050
Iteration: 432, Log-Lik: -2653.520, Max-Change: 0.00051
Iteration: 433, Log-Lik: -2653.520, Max-Change: 0.00010
Iteration: 434, Log-Lik: -2653.520, Max-Change: 0.00049
Iteration: 435, Log-Lik: -2653.520, Max-Change: 0.00051
Iteration: 436, Log-Lik: -2653.520, Max-Change: 0.00010

itemplot(mod1, 2)

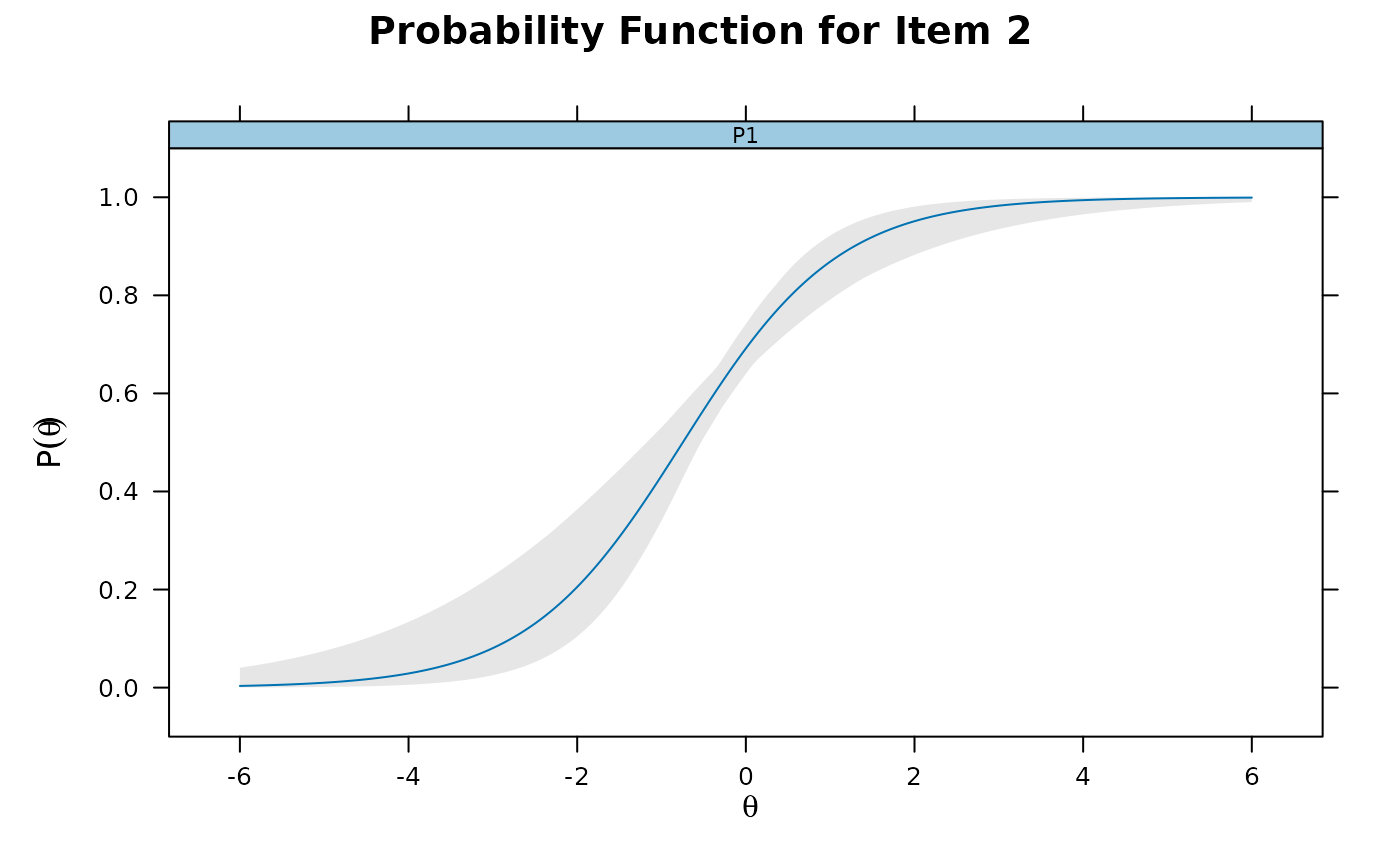
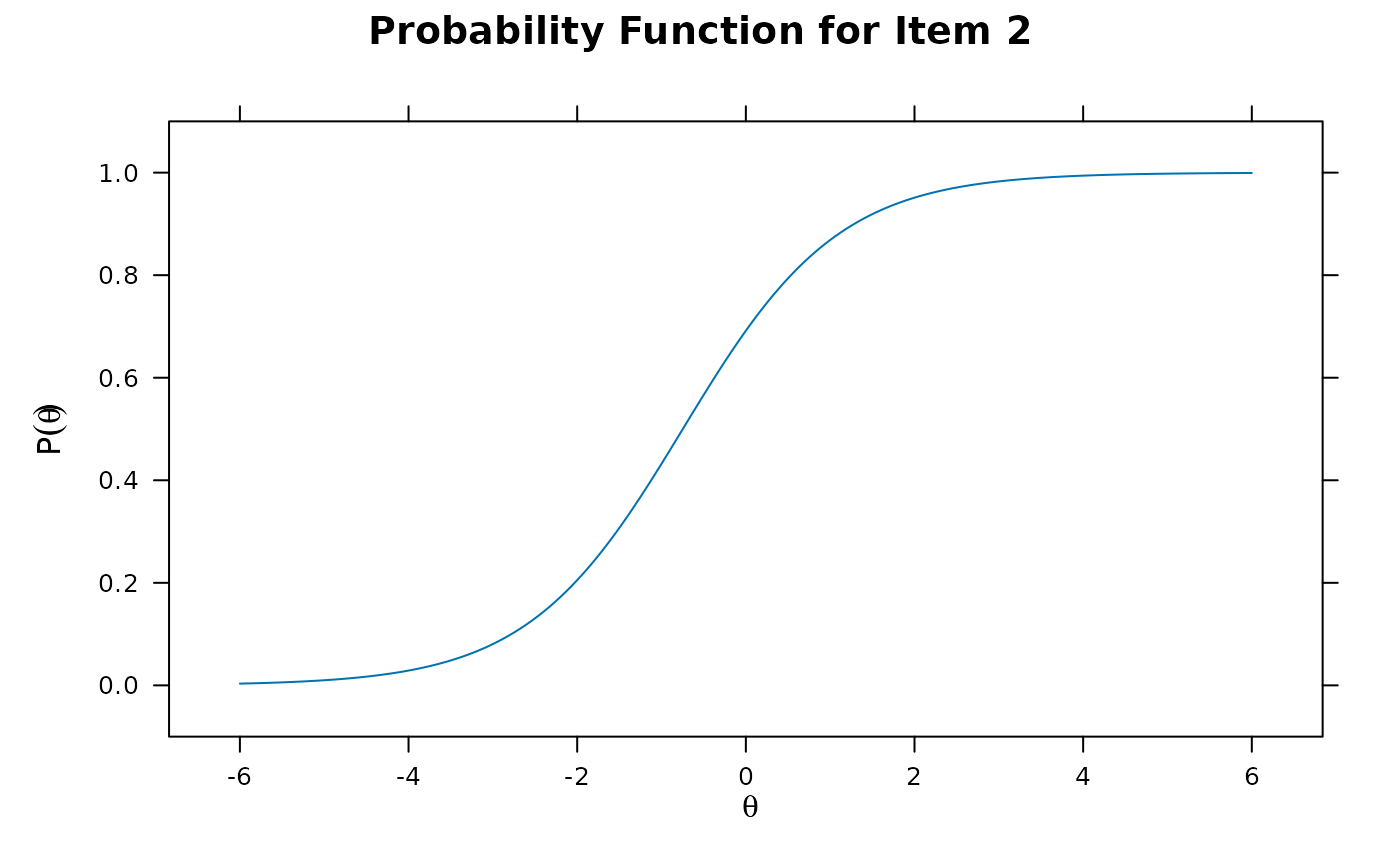itemplot(mod1, 2, CE = TRUE)

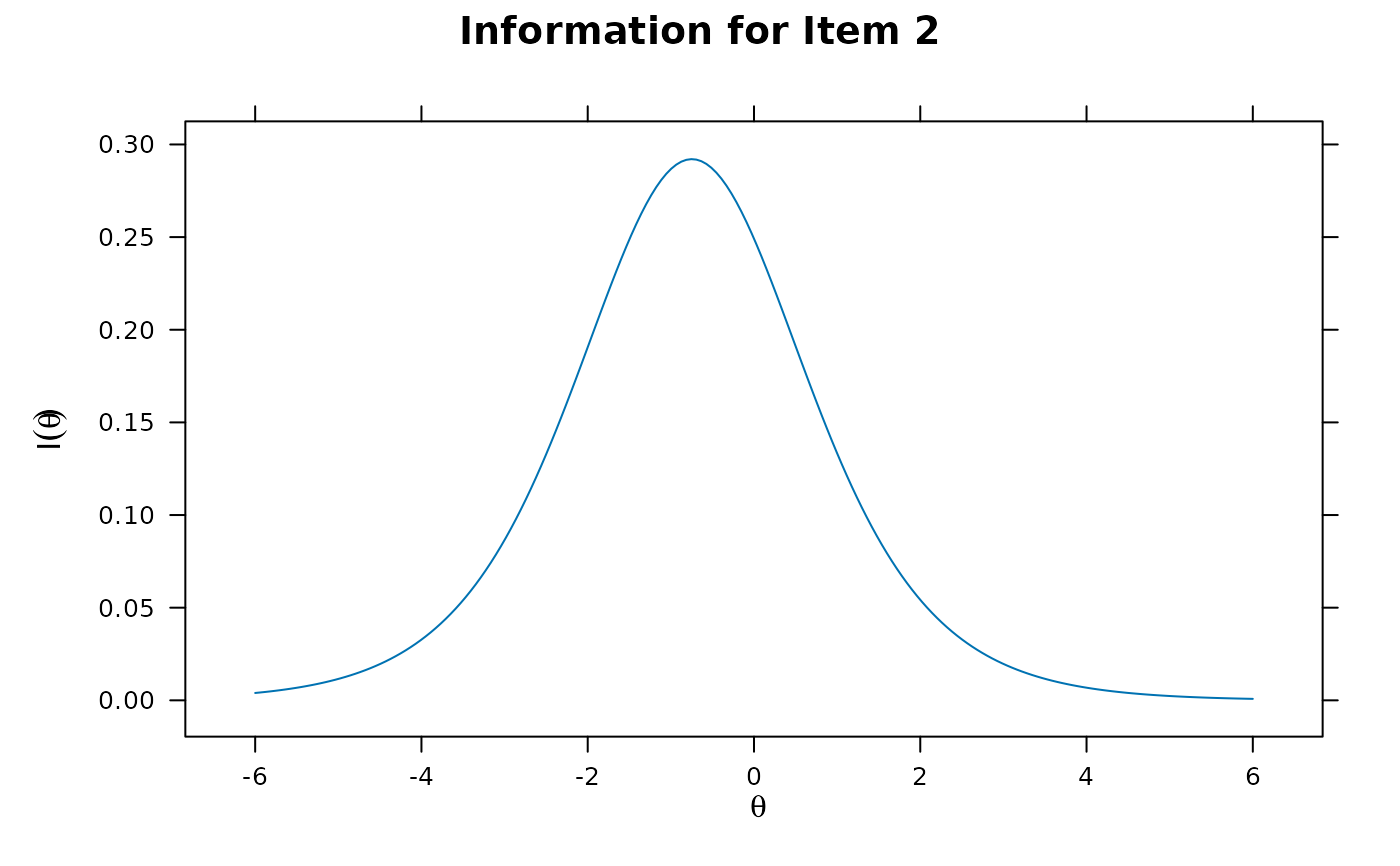
itemplot(mod1, 2, type = 'info')

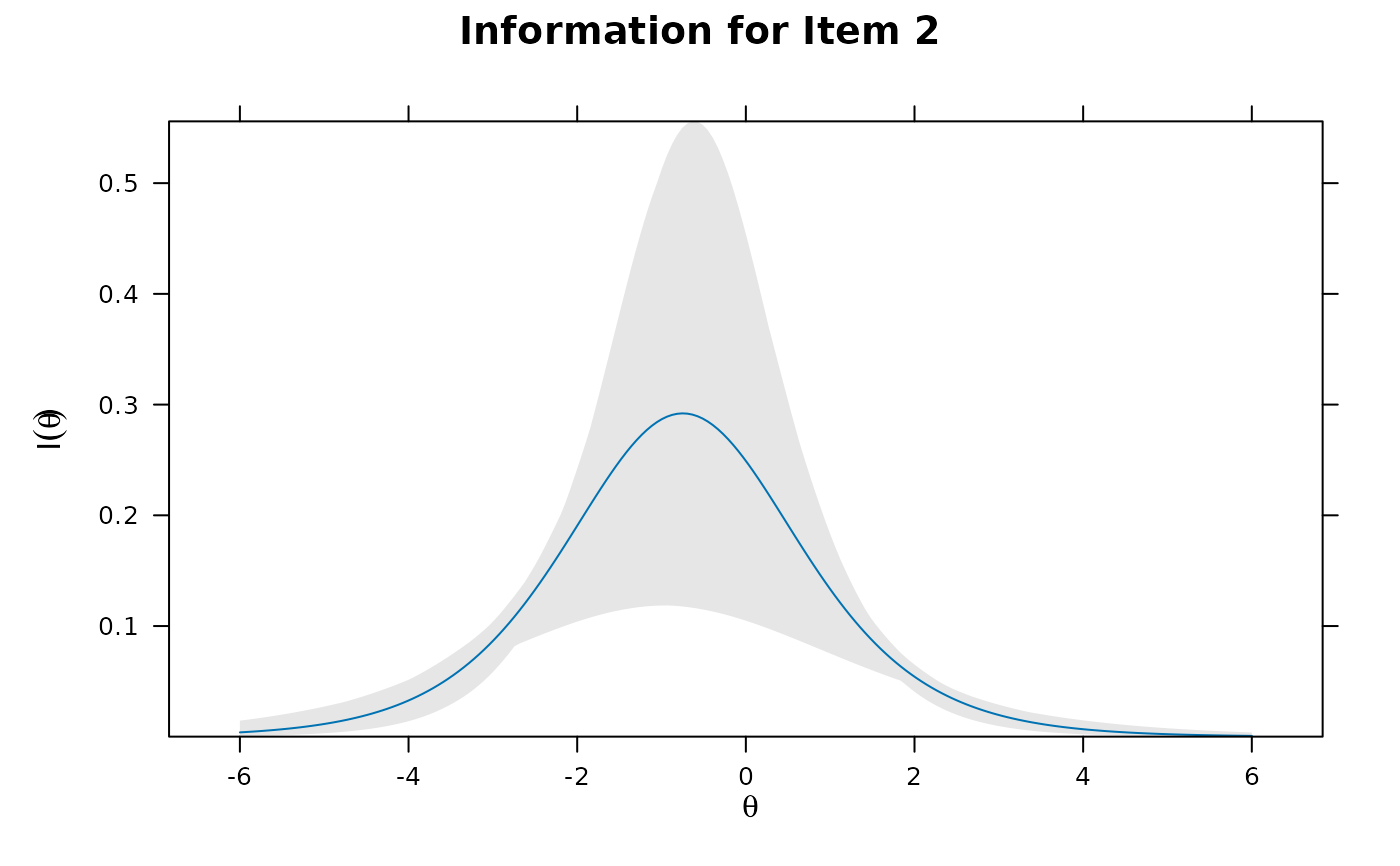
itemplot(mod1, 2, type = 'info', CE = TRUE)


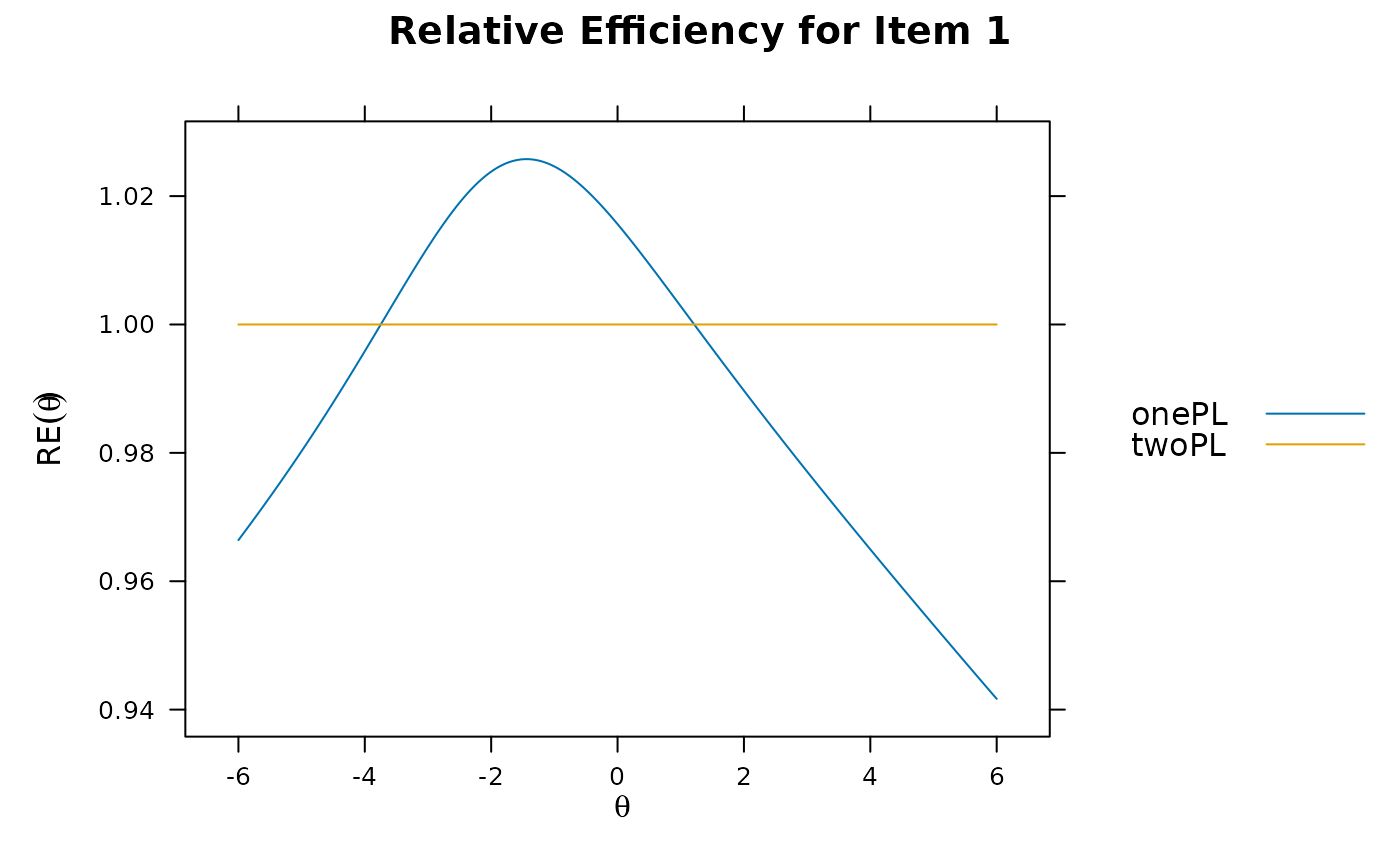
mods <- list(twoPL = mod1, onePL = mod2)
itemplot(mods, 1, type = 'RE')


# multidimensional
itemplot(mod3, 4, type = 'info')

itemplot(mod3, 4, type = 'info',
  col.regions = colorRampPalette(c("white", "red"))(100))

itemplot(mod3, 4, type = 'infocontour')

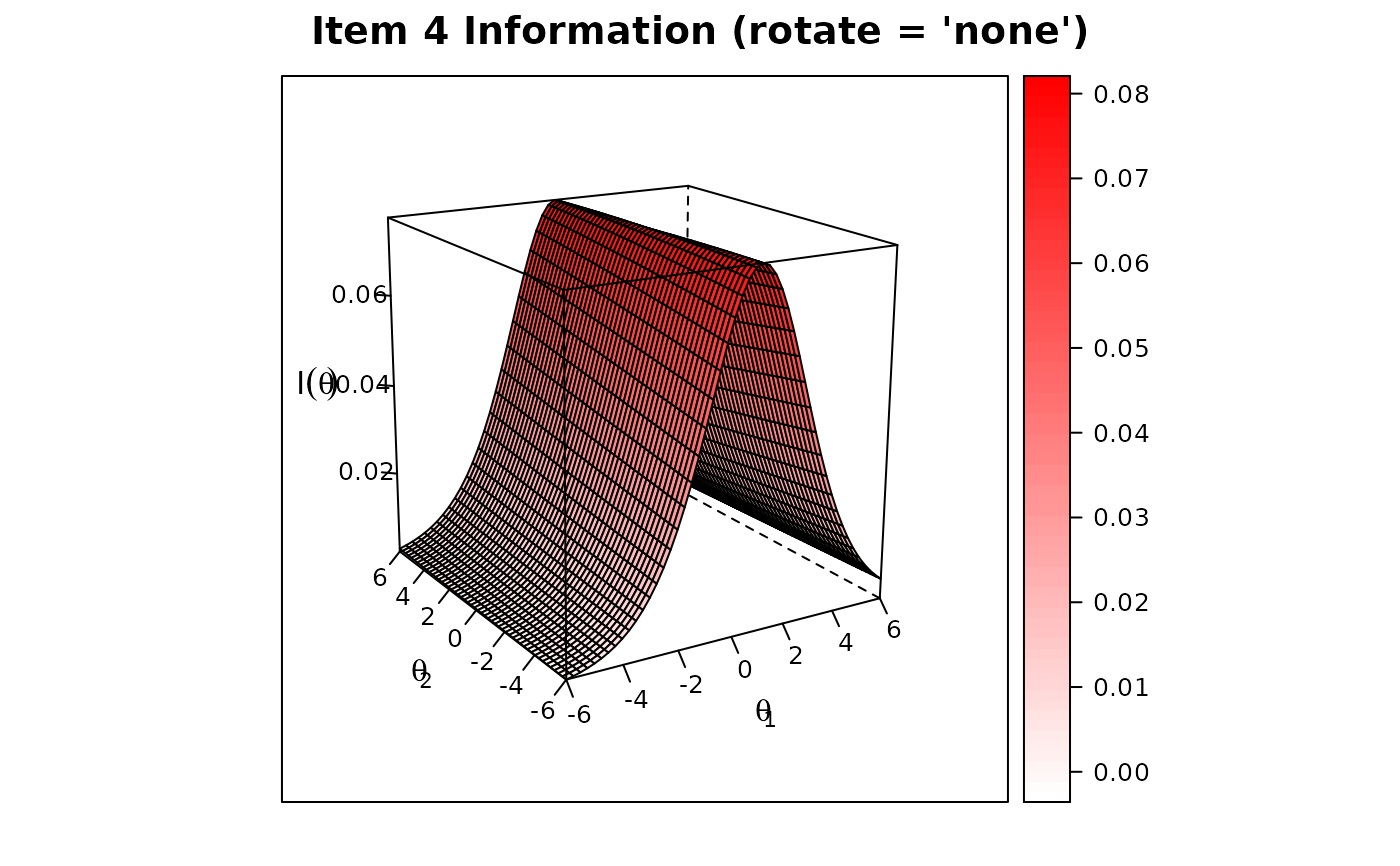
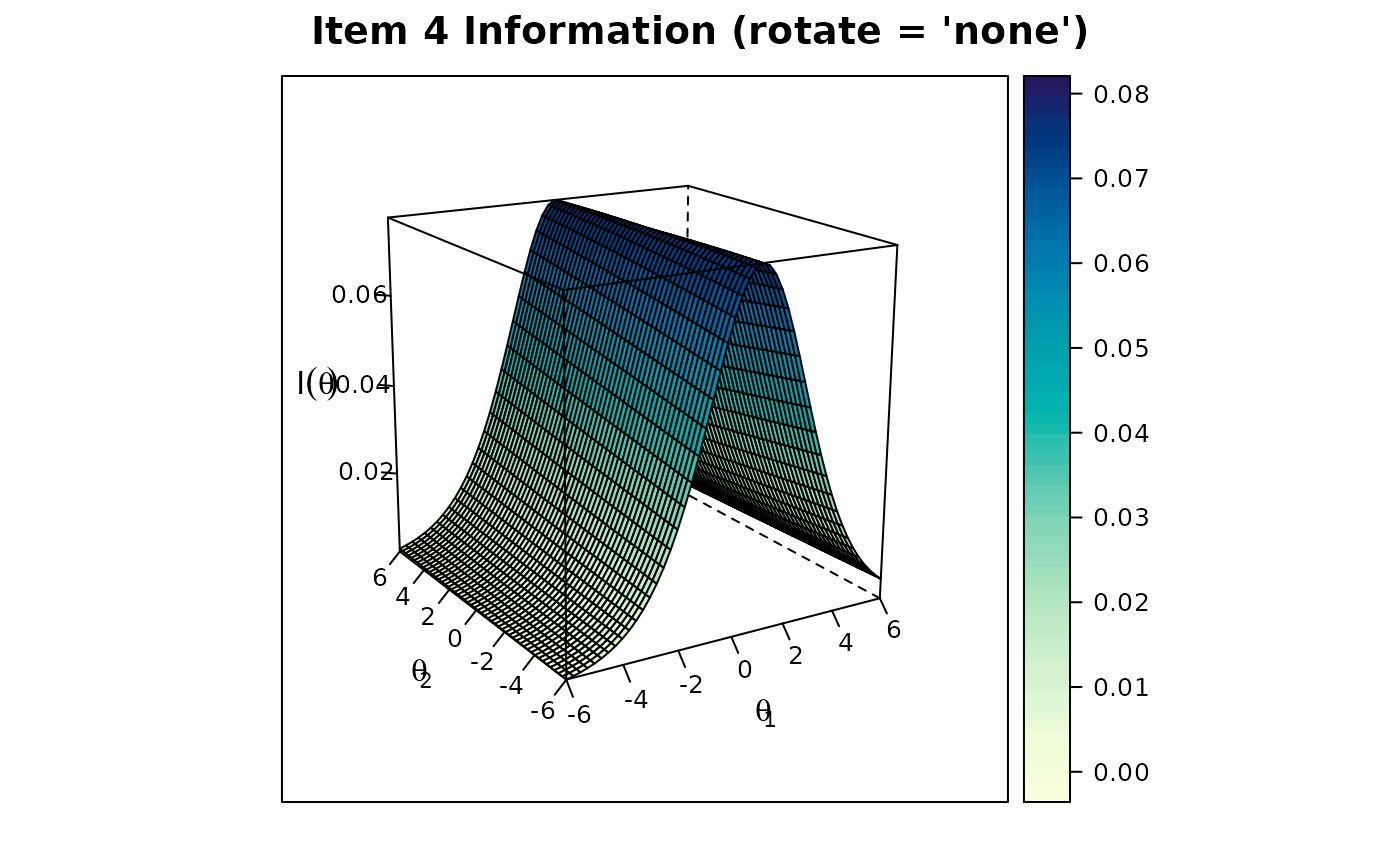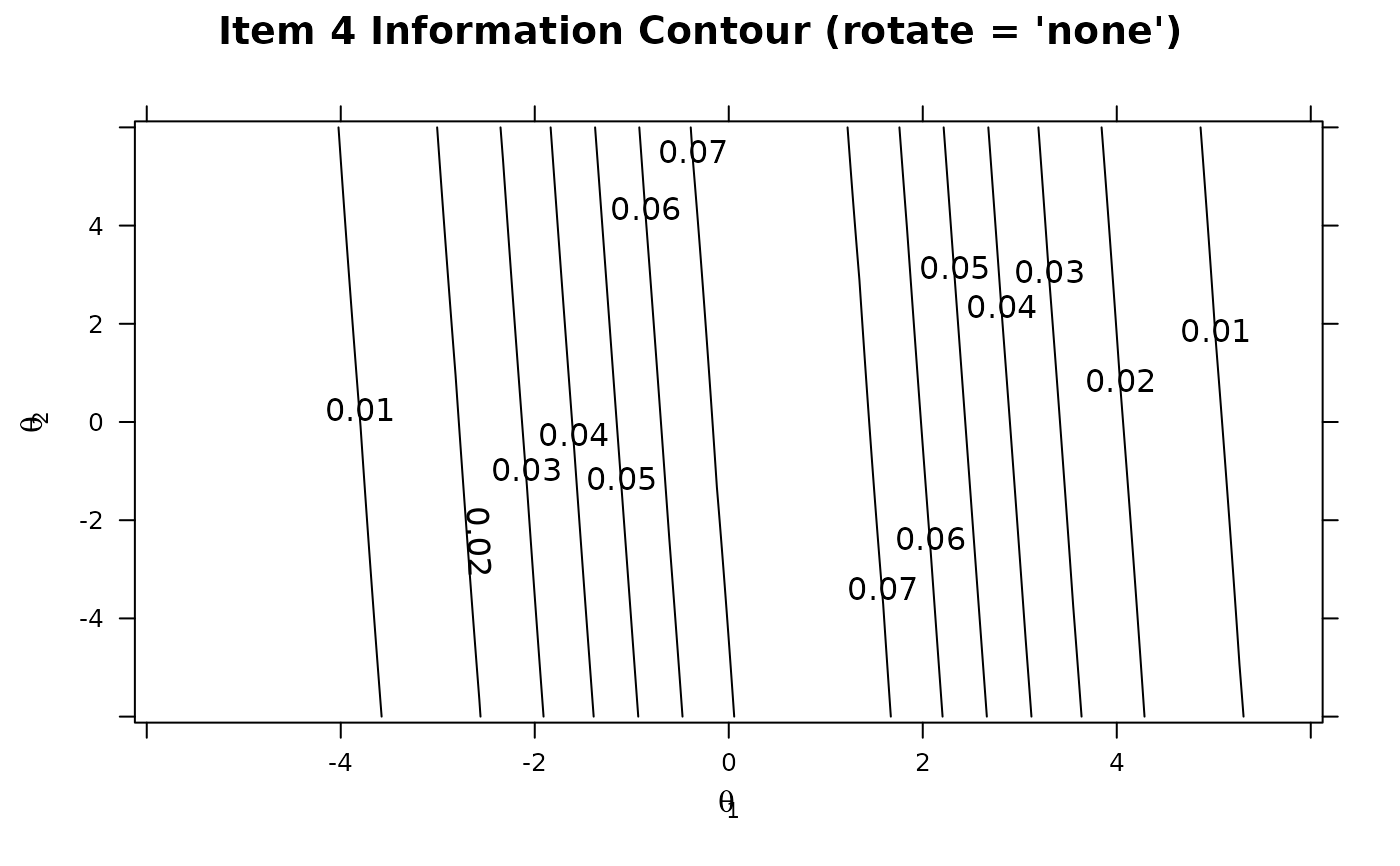
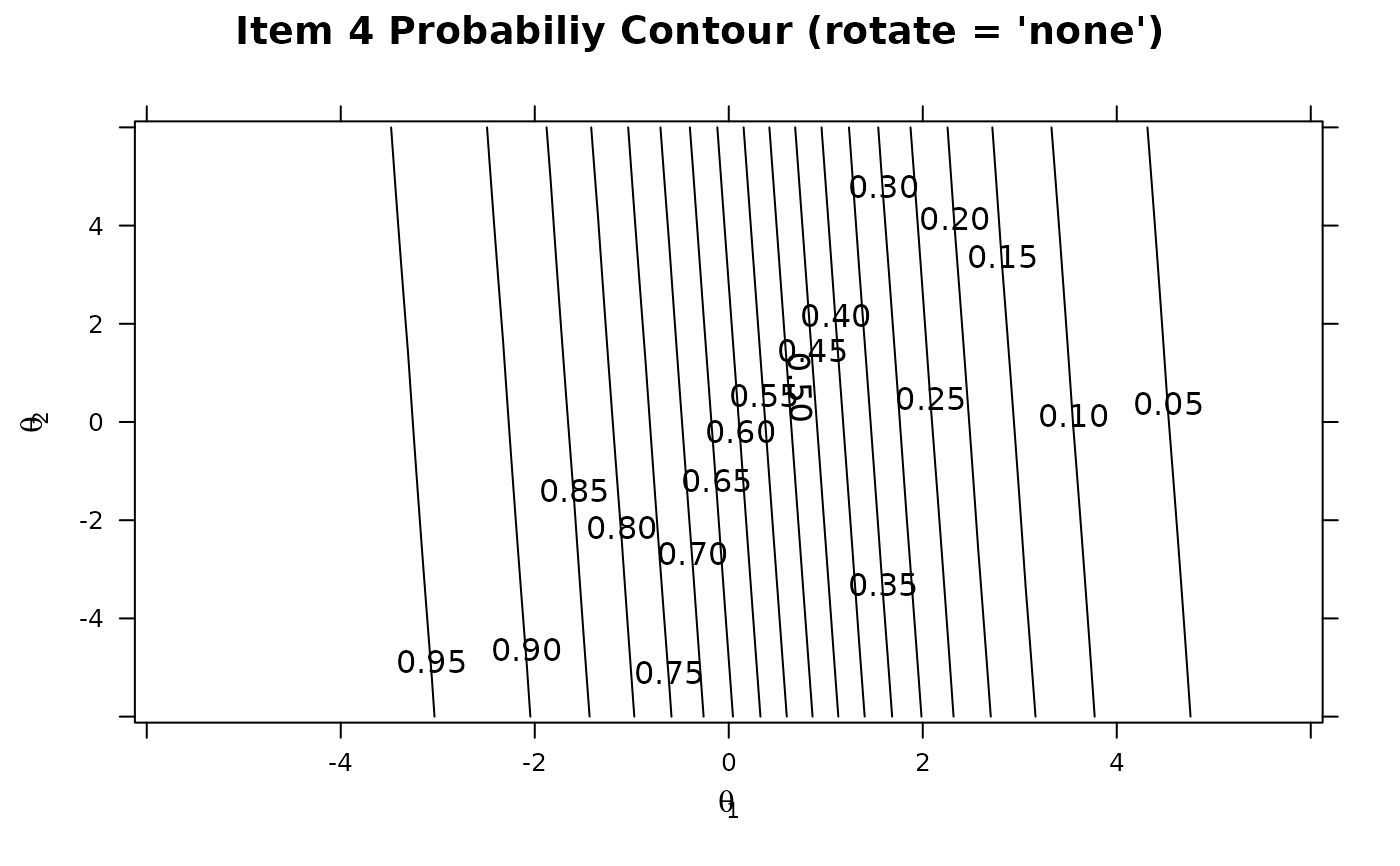
itemplot(mod3, 4, type = 'tracecontour')


# polytomous items
pmod <- mirt(Science, 1, SE=TRUE)
#> 
Iteration: 1, Log-Lik: -1629.361, Max-Change: 0.50660
Iteration: 2, Log-Lik: -1617.374, Max-Change: 0.25442
Iteration: 3, Log-Lik: -1612.894, Max-Change: 0.16991
Iteration: 4, Log-Lik: -1610.306, Max-Change: 0.10461
Iteration: 5, Log-Lik: -1609.814, Max-Change: 0.09162
Iteration: 6, Log-Lik: -1609.534, Max-Change: 0.07363
Iteration: 7, Log-Lik: -1609.030, Max-Change: 0.03677
Iteration: 8, Log-Lik: -1608.988, Max-Change: 0.03200
Iteration: 9, Log-Lik: -1608.958, Max-Change: 0.02754
Iteration: 10, Log-Lik: -1608.878, Max-Change: 0.01443
Iteration: 11, Log-Lik: -1608.875, Max-Change: 0.00847
Iteration: 12, Log-Lik: -1608.873, Max-Change: 0.00515
Iteration: 13, Log-Lik: -1608.872, Max-Change: 0.00550
Iteration: 14, Log-Lik: -1608.872, Max-Change: 0.00318
Iteration: 15, Log-Lik: -1608.871, Max-Change: 0.00462
Iteration: 16, Log-Lik: -1608.871, Max-Change: 0.00277
Iteration: 17, Log-Lik: -1608.870, Max-Change: 0.00145
Iteration: 18, Log-Lik: -1608.870, Max-Change: 0.00175
Iteration: 19, Log-Lik: -1608.870, Max-Change: 0.00126
Iteration: 20, Log-Lik: -1608.870, Max-Change: 0.00025
Iteration: 21, Log-Lik: -1608.870, Max-Change: 0.00285
Iteration: 22, Log-Lik: -1608.870, Max-Change: 0.00108
Iteration: 23, Log-Lik: -1608.870, Max-Change: 0.00022
Iteration: 24, Log-Lik: -1608.870, Max-Change: 0.00059
Iteration: 25, Log-Lik: -1608.870, Max-Change: 0.00014
Iteration: 26, Log-Lik: -1608.870, Max-Change: 0.00068
Iteration: 27, Log-Lik: -1608.870, Max-Change: 0.00065
Iteration: 28, Log-Lik: -1608.870, Max-Change: 0.00019
Iteration: 29, Log-Lik: -1608.870, Max-Change: 0.00061
Iteration: 30, Log-Lik: -1608.870, Max-Change: 0.00012
Iteration: 31, Log-Lik: -1608.870, Max-Change: 0.00012
Iteration: 32, Log-Lik: -1608.870, Max-Change: 0.00058
Iteration: 33, Log-Lik: -1608.870, Max-Change: 0.00055
Iteration: 34, Log-Lik: -1608.870, Max-Change: 0.00015
Iteration: 35, Log-Lik: -1608.870, Max-Change: 0.00052
Iteration: 36, Log-Lik: -1608.870, Max-Change: 0.00010
#> 
#> Calculating information matrix...
itemplot(pmod, 3)

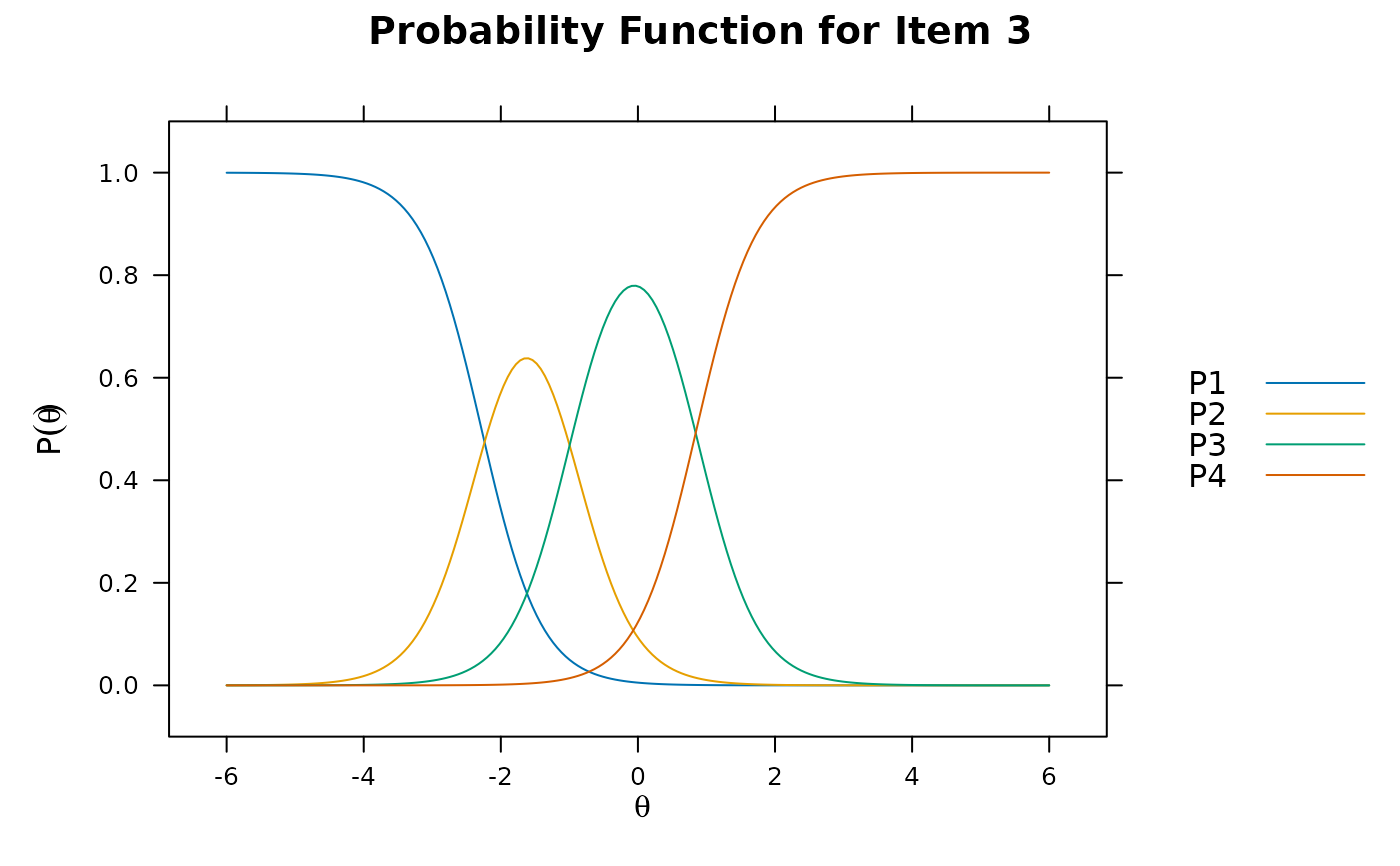itemplot(pmod, 3, type = 'threshold')

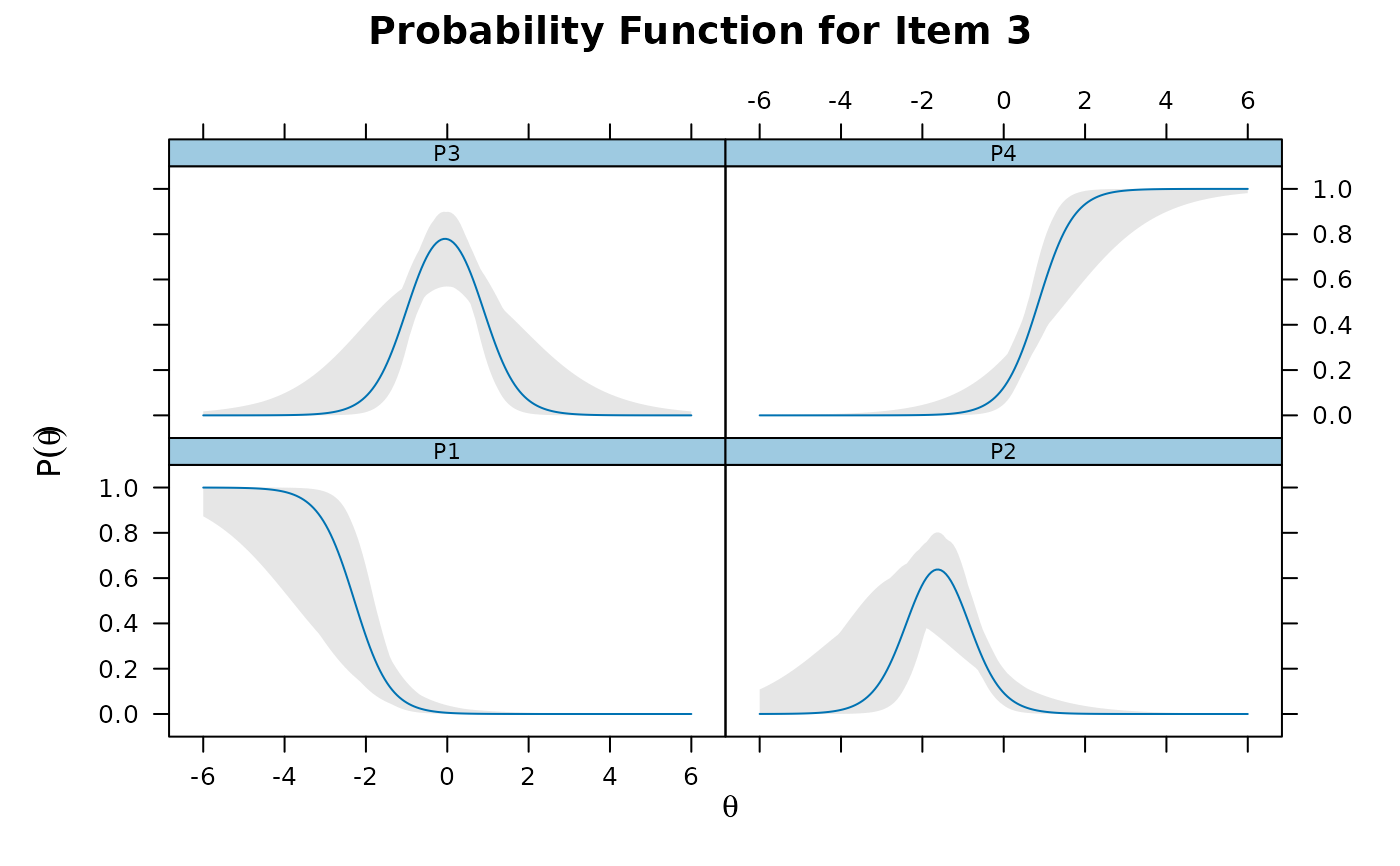
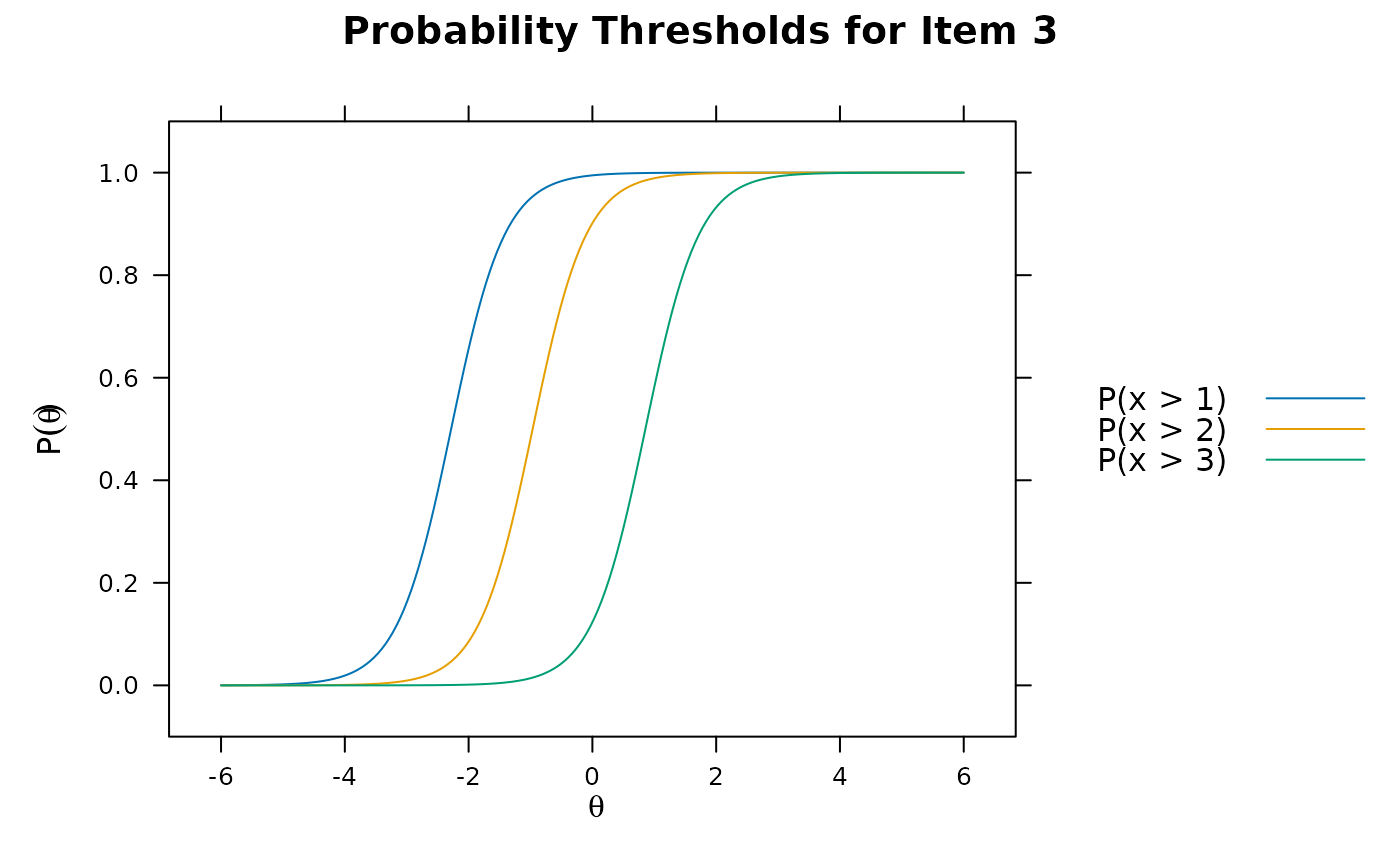itemplot(pmod, 3, CE = TRUE)

itemplot(pmod, 3, type = 'score')

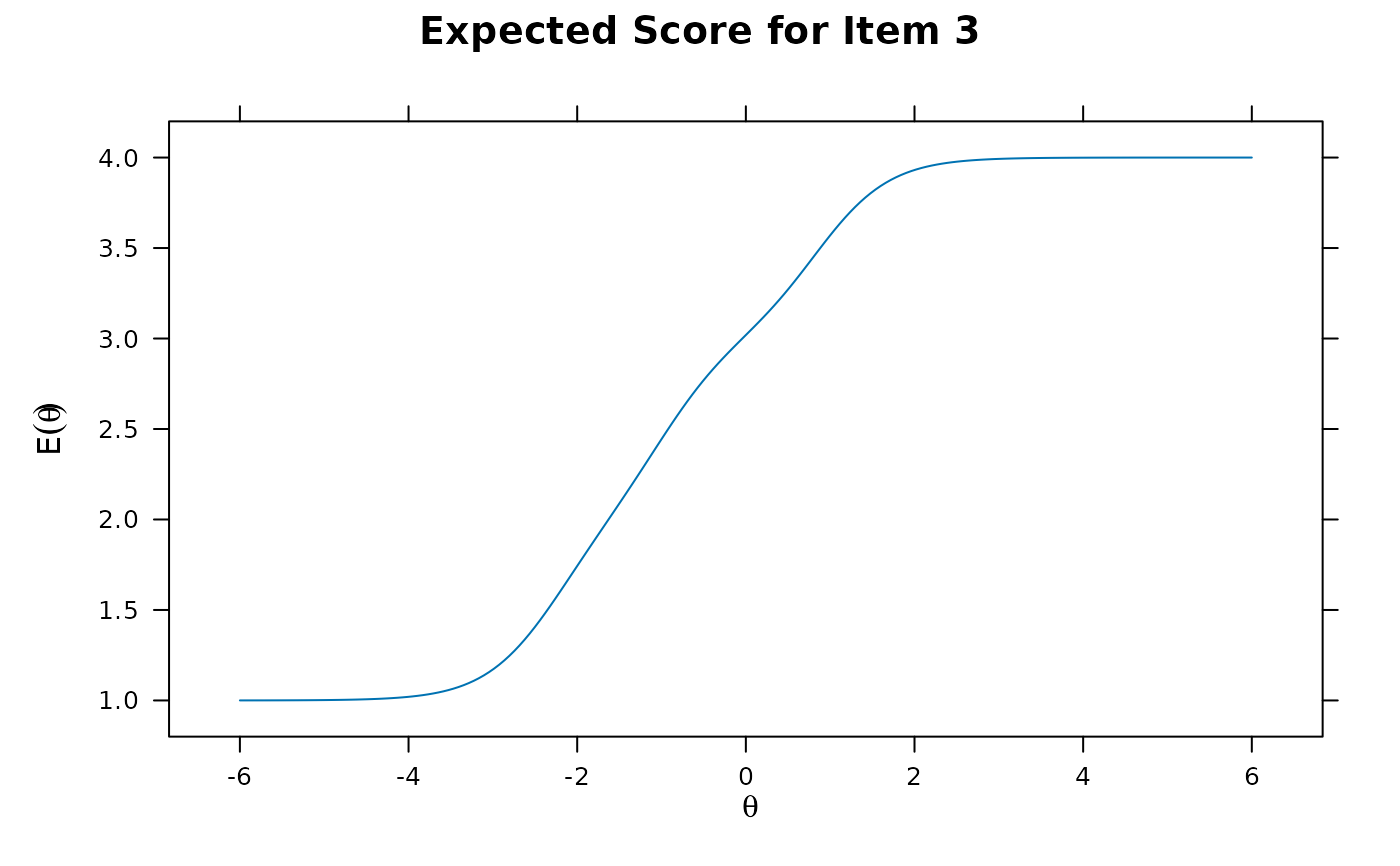itemplot(pmod, 3, type = 'score', CE = TRUE)

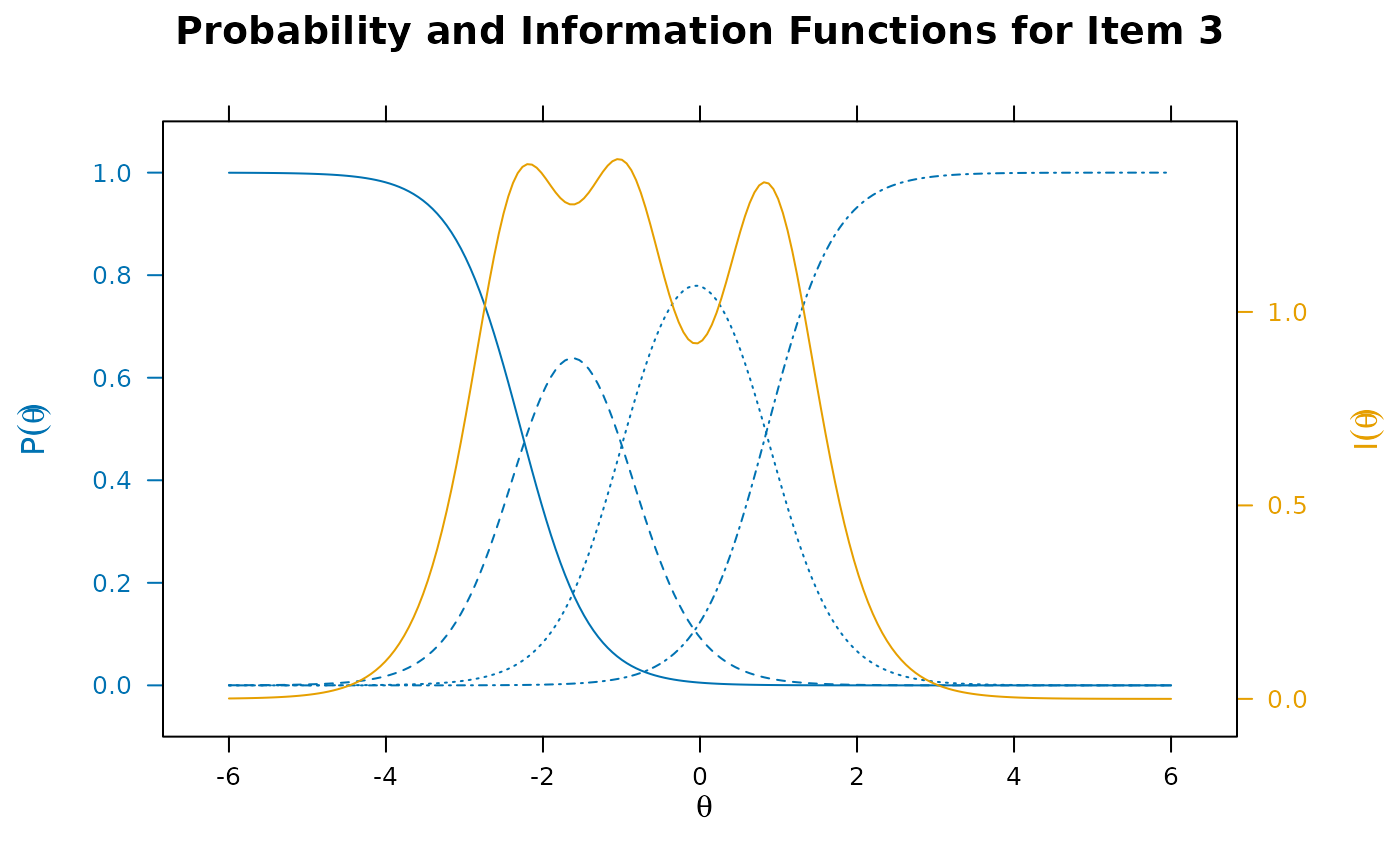
itemplot(pmod, 3, type = 'infotrace')

itemplot(pmod, 3, type = 'infocat')



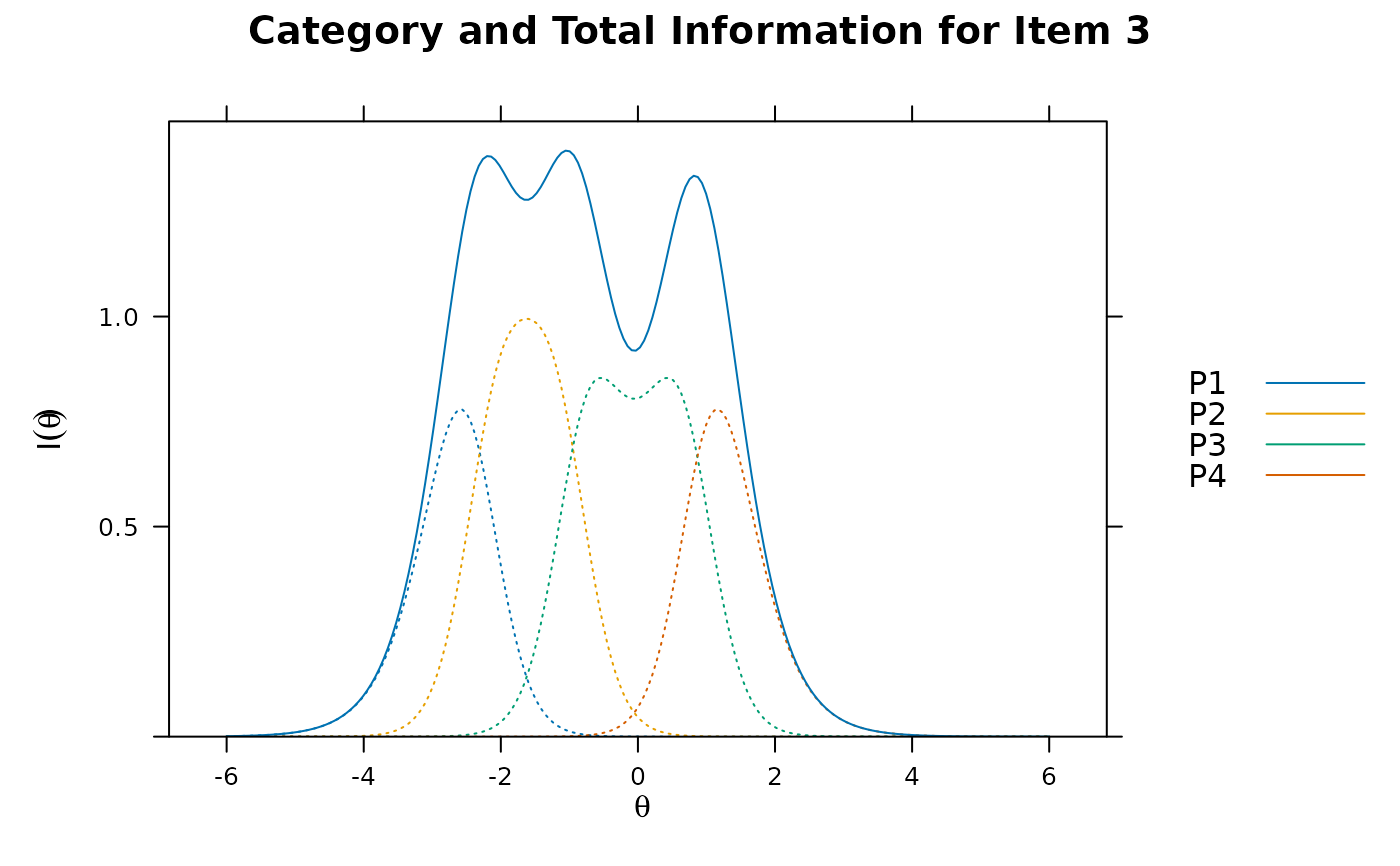# use the directlabels package to put labels on tracelines
library(directlabels)
plt <- itemplot(pmod, 3)
direct.label(plt, 'top.points')


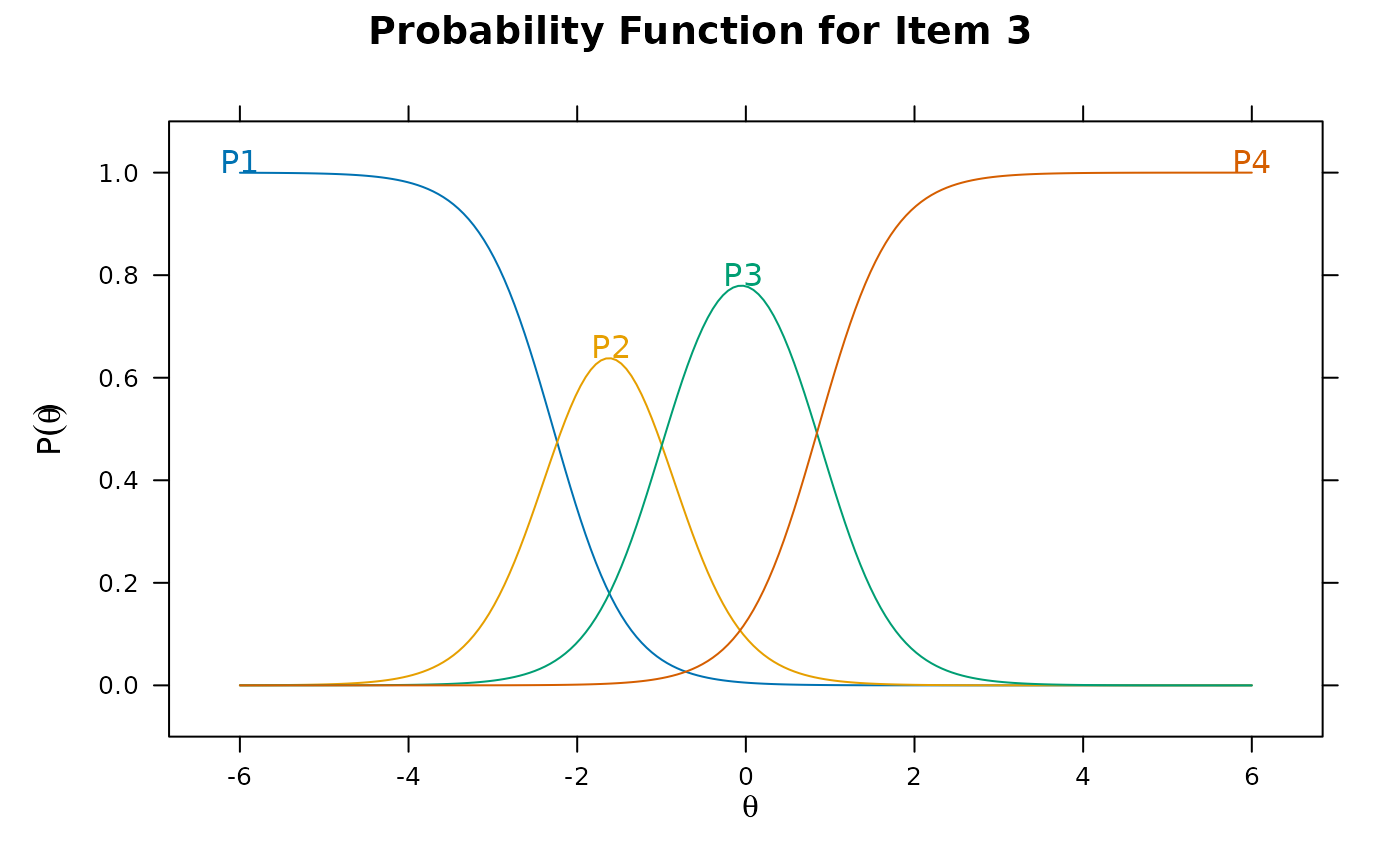# change colour theme of plots
bwtheme <- standard.theme("pdf", color=FALSE)
plot(pmod, type='trace', par.settings=bwtheme)

itemplot(pmod, 1, type = 'trace', par.settings=bwtheme)


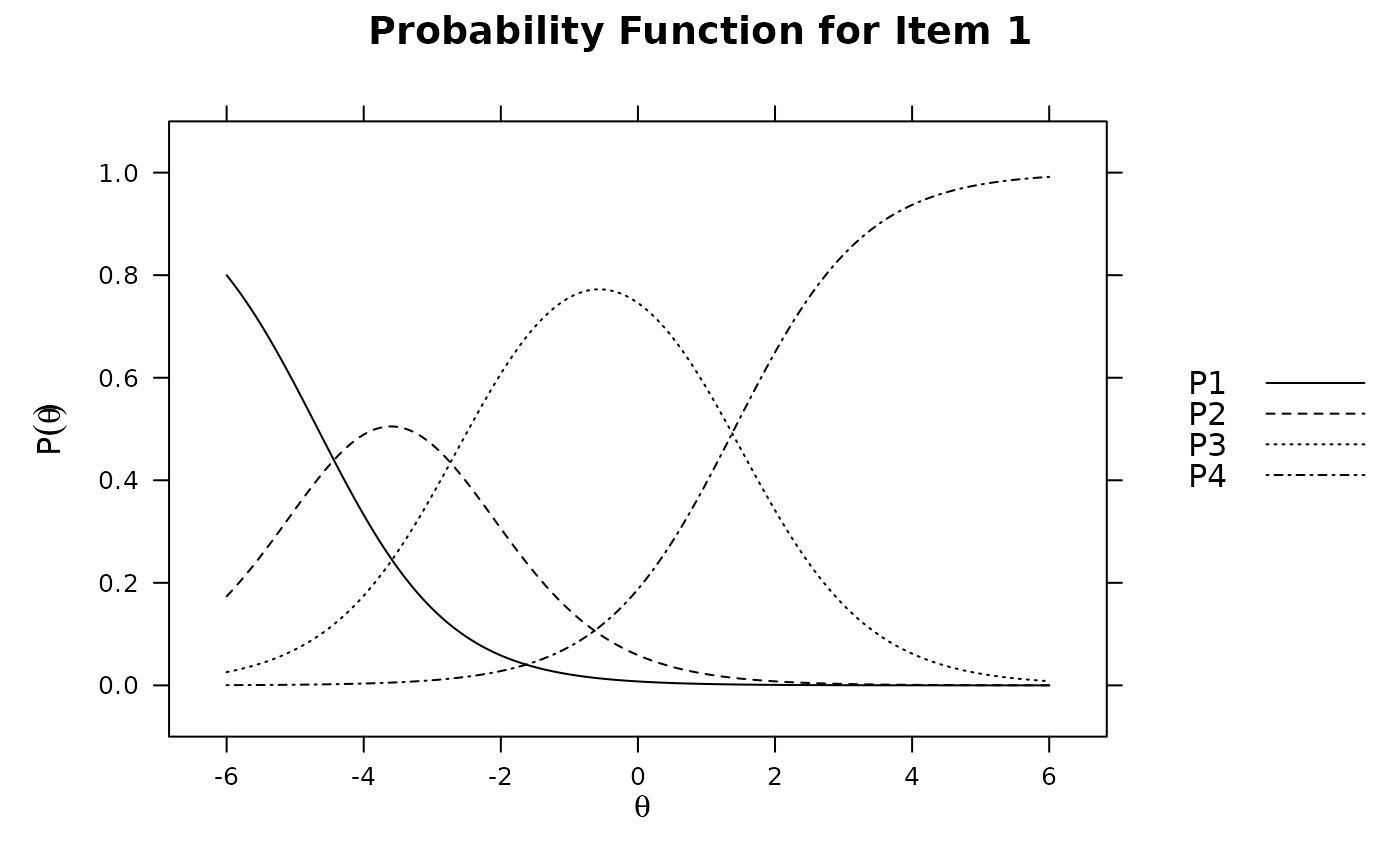# additional modifications can be made via update().
# See ?update.trellis for further documentation
(plt <- itemplot(pmod, 1))

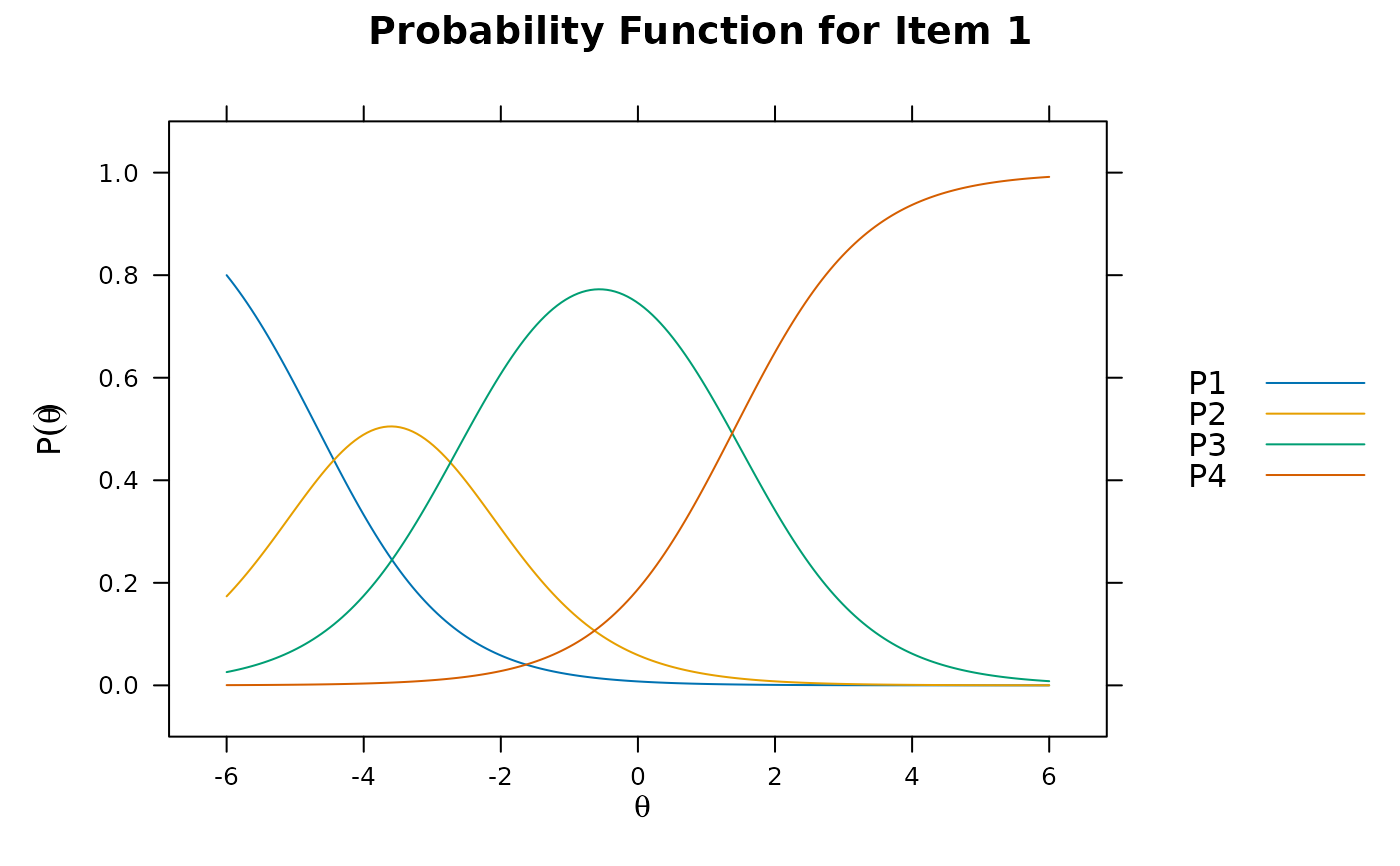update(plt, ylab = expression(Prob(theta))) # ylab changed


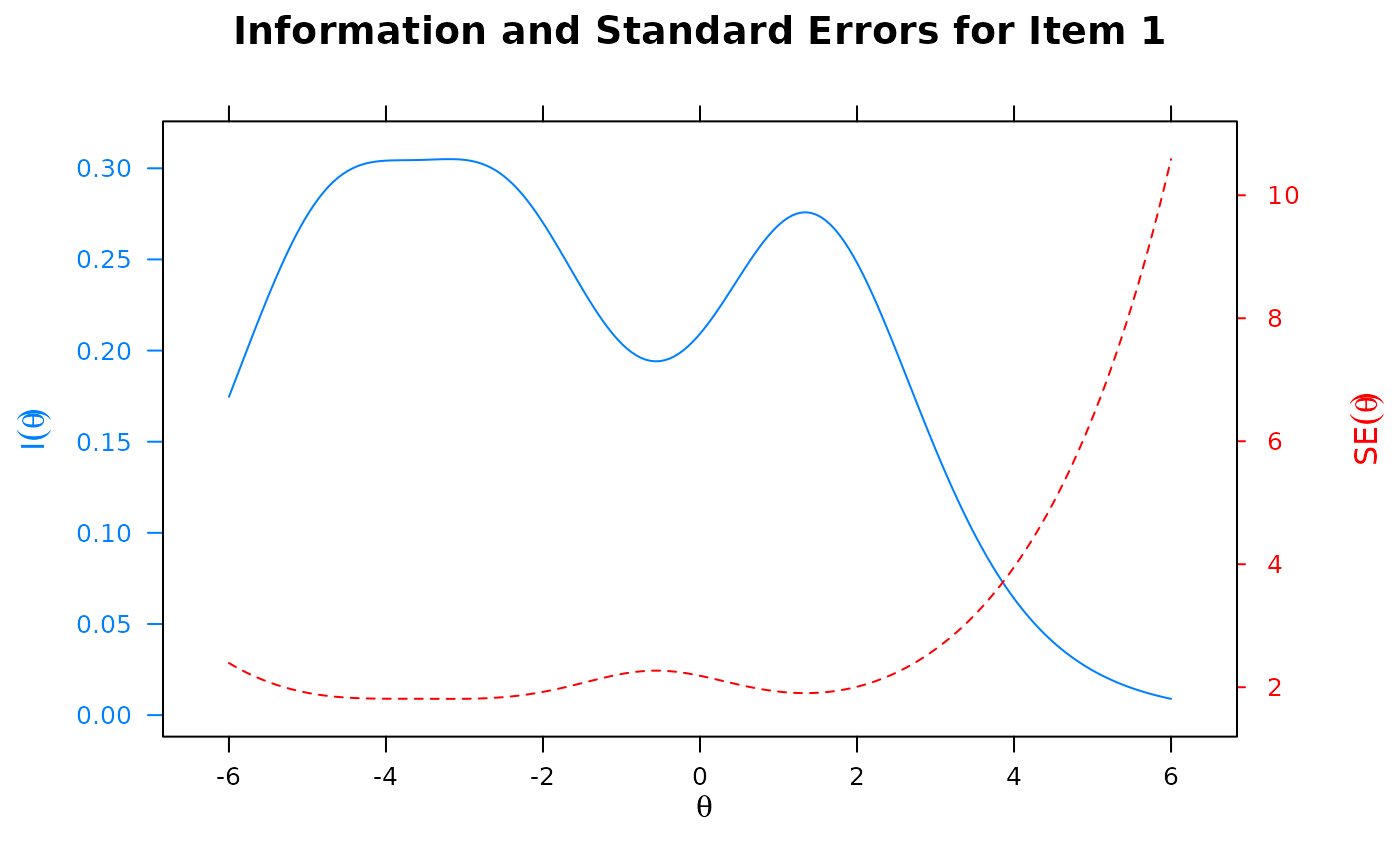
# infoSE plot
itemplot(pmod, 1, type = 'infoSE')


# uncomment to run interactive shiny applet
# itemplot(shiny = TRUE)
    # }