Translate mirt parameters into suitable structure for plink package
Source:R/read.mirt.R
read.mirt.RdThis function exports item parameters from the mirt package to the
plink package.
Arguments
- x
a single object (or list of objects) returned from
mirt, bfactor, or a single object returned bymultipleGroup- as.irt.pars
if
TRUE, the parameters will be output as anirt.parsobject- ...
additional arguments to be passed to
coef()
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
# \donttest{
## unidimensional
library(plink)
data <- expand.table(LSAT7)
(mod1 <- mirt(data, 1))
#>
#> Call:
#> mirt(data = data, model = 1)
#>
#> Full-information item factor analysis with 1 factor(s).
#> Converged within 1e-04 tolerance after 28 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: BFGS
#> EM acceleration: Ramsay
#> Number of rectangular quadrature: 61
#> Latent density type: Gaussian
#>
#> Log-likelihood = -2658.805
#> Estimated parameters: 10
#> AIC = 5337.61
#> BIC = 5386.688; SABIC = 5354.927
#> G2 (21) = 31.7, p = 0.0628
#> RMSEA = 0.023, CFI = NaN, TLI = NaN
plinkpars <- read.mirt(mod1)
plot(plinkpars)
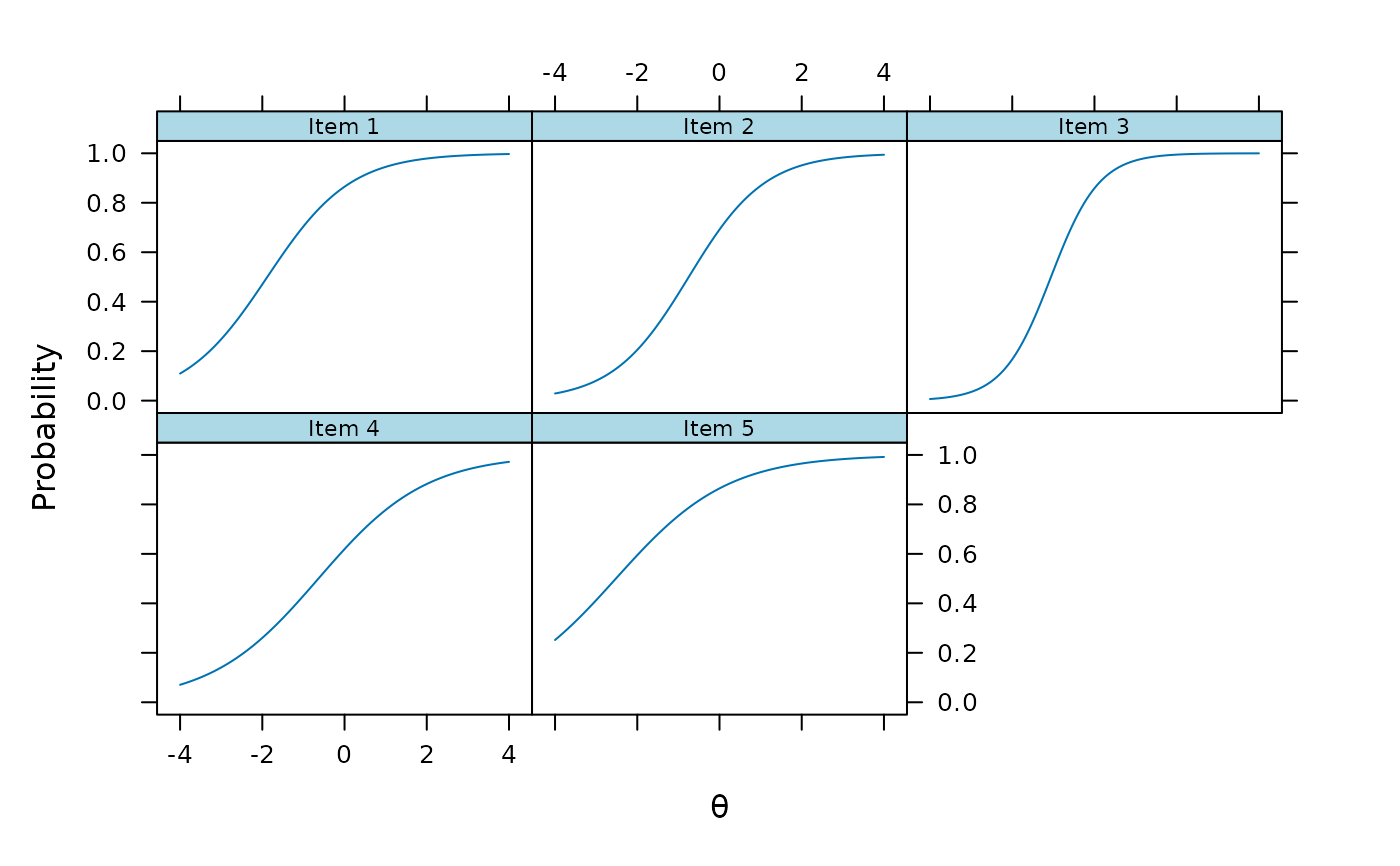 plot(mod1, type = 'trace')
plot(mod1, type = 'trace')
 # graded
mod2 <- mirt(Science, 1)
plinkpars <- read.mirt(mod2)
plot(plinkpars)
# graded
mod2 <- mirt(Science, 1)
plinkpars <- read.mirt(mod2)
plot(plinkpars)
 plot(mod2, type = 'trace')
plot(mod2, type = 'trace')
 # gpcm
mod3 <- mirt(Science, 1, itemtype = 'gpcm')
plinkpars <- read.mirt(mod3)
plot(plinkpars)
# gpcm
mod3 <- mirt(Science, 1, itemtype = 'gpcm')
plinkpars <- read.mirt(mod3)
plot(plinkpars)
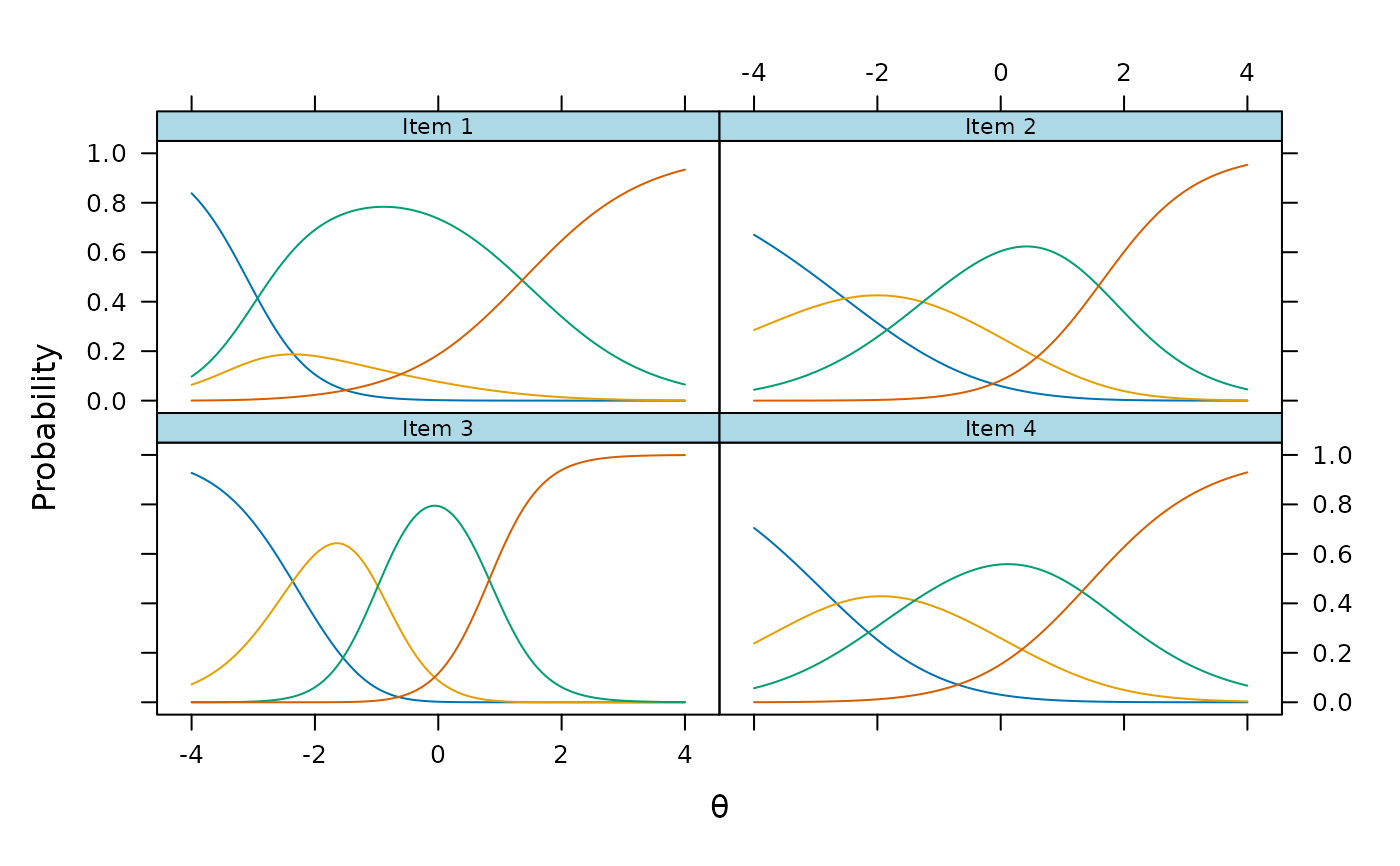
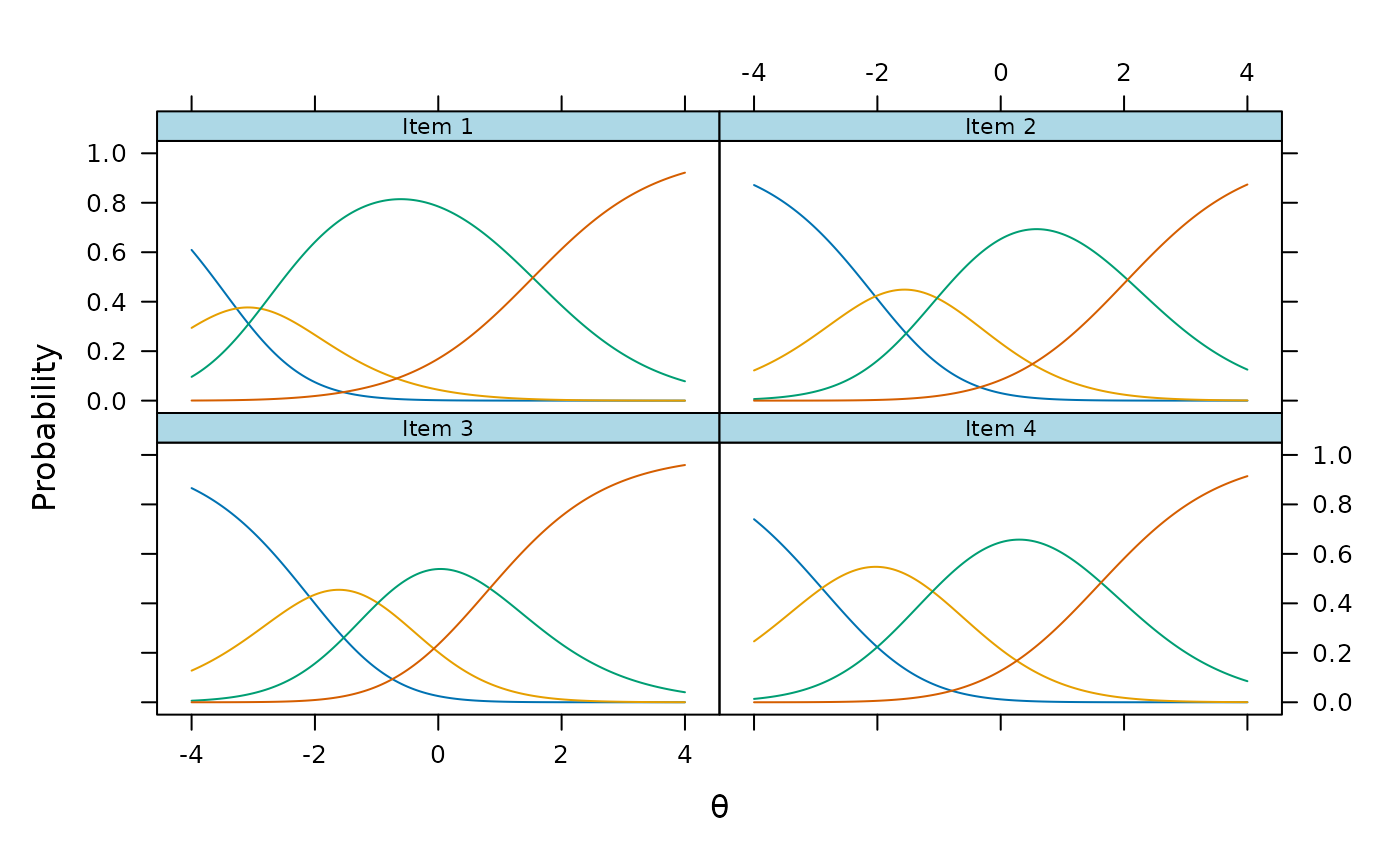 plot(mod3, type = 'trace')
plot(mod3, type = 'trace')
 # nominal
mod4 <- mirt(Science, 1, itemtype = 'nominal')
plinkpars <- read.mirt(mod4)
plot(plinkpars)
# nominal
mod4 <- mirt(Science, 1, itemtype = 'nominal')
plinkpars <- read.mirt(mod4)
plot(plinkpars)
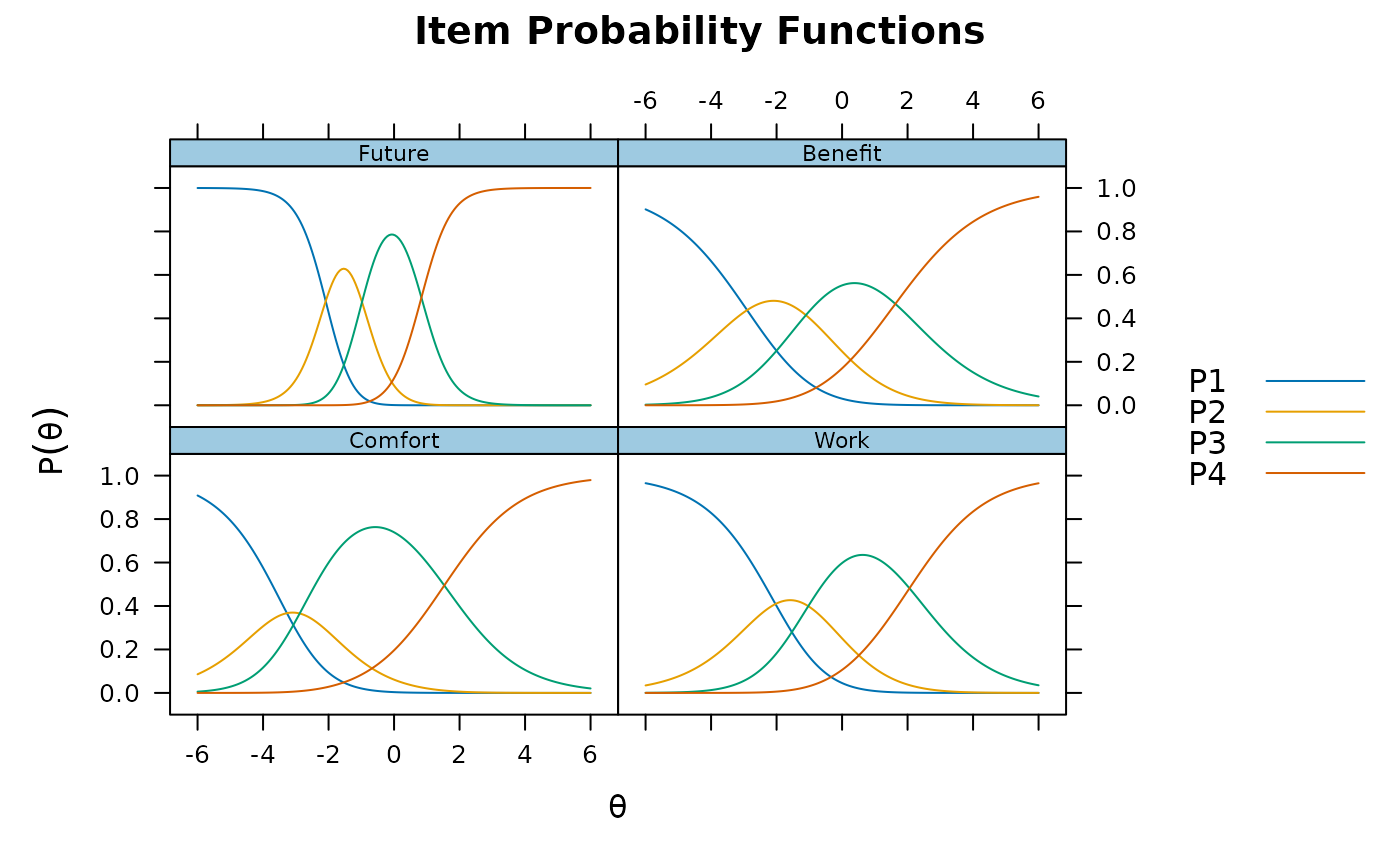
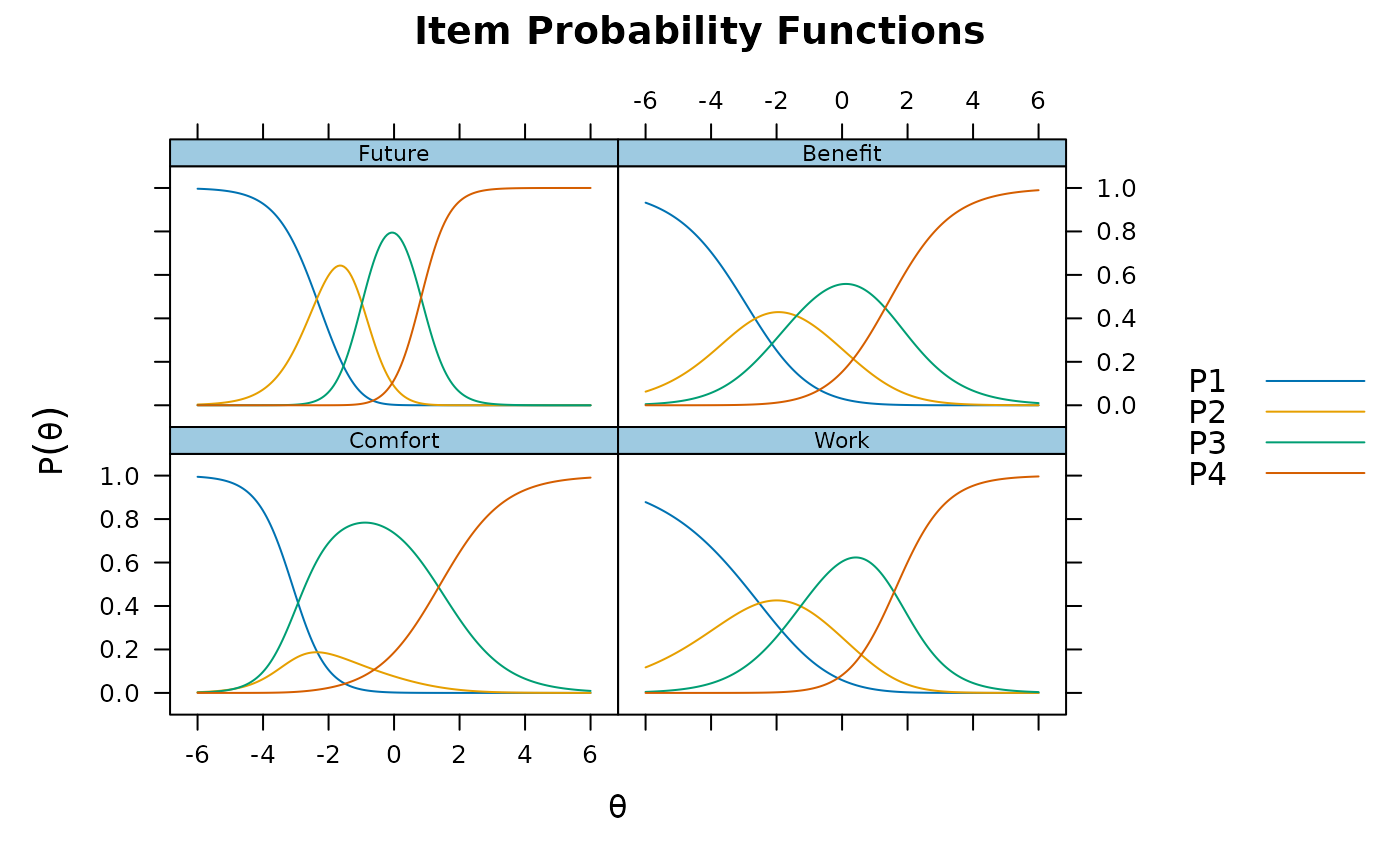
 plot(mod4, type = 'trace')
plot(mod4, type = 'trace')
 ## multidimensional
data <- expand.table(LSAT7)
(mod1 <- mirt(data, 2))
#>
#> Call:
#> mirt(data = data, model = 2)
#>
#> Full-information item factor analysis with 2 factor(s).
#> Converged within 1e-04 tolerance after 436 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: BFGS
#> EM acceleration: Ramsay
#> Number of rectangular quadrature: 31
#> Latent density type: Gaussian
#>
#> Log-likelihood = -2653.52
#> Estimated parameters: 14
#> AIC = 5335.039
#> BIC = 5403.748; SABIC = 5359.283
#> G2 (17) = 21.13, p = 0.2205
#> RMSEA = 0.016, CFI = NaN, TLI = NaN
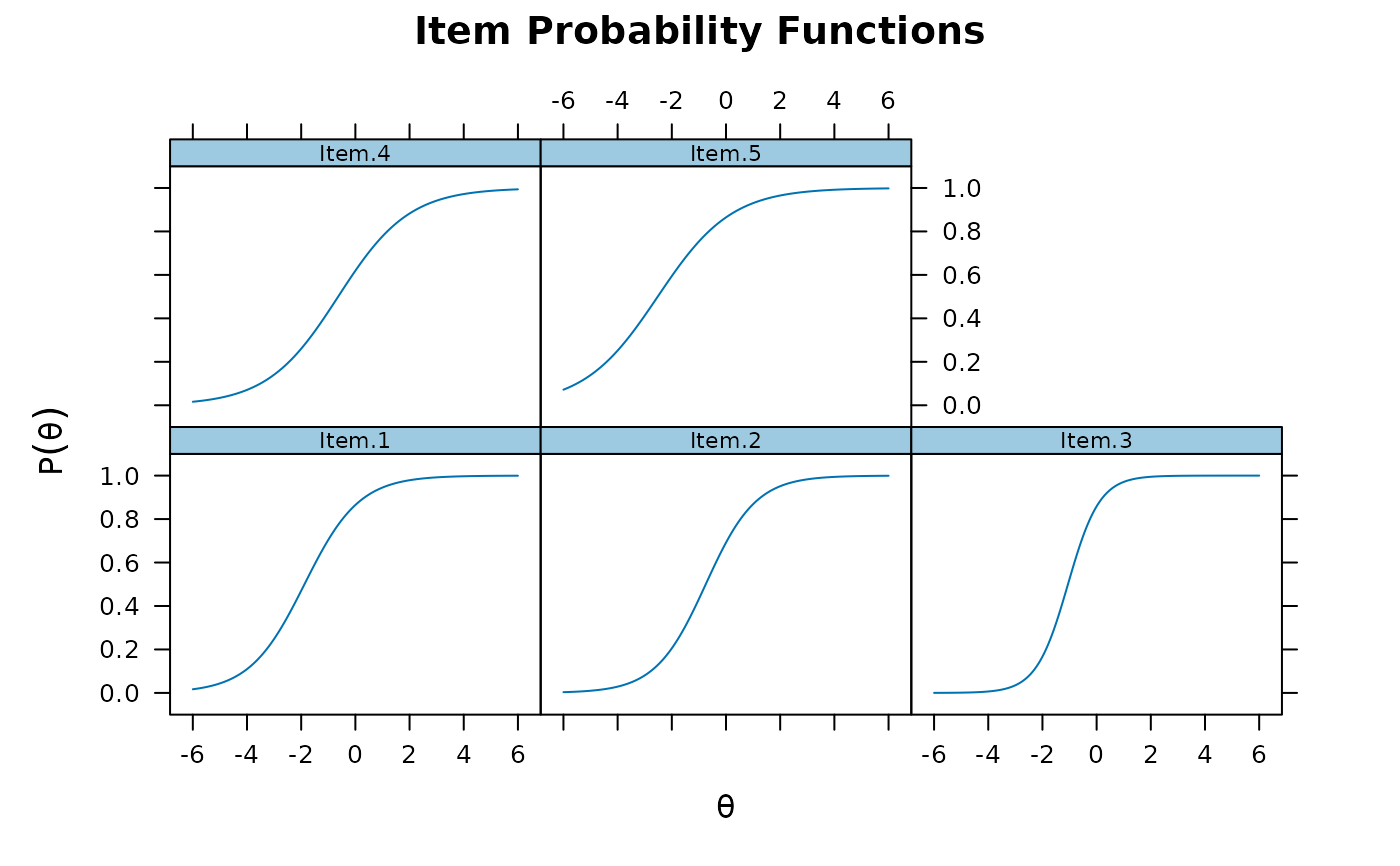
plinkpars <- read.mirt(mod1)
plinkpars
#> An object of class "irt.pars"
#> Slot "pars":
#> a1 a2
#> [1,] -2.0072336 0.87037703 2.6479635 0
#> [2,] -0.8488425 -0.52210644 0.7876378 0
#> [3,] -2.1530084 -1.83652628 2.4829929 0
#> [4,] -0.7558975 -0.02803433 0.4847282 0
#> [5,] -0.7572717 0.00000000 1.8640953 0
#>
#> Slot "cat":
#> [1] 2 2 2 2 2
#>
#> Slot "poly.mod":
#> An object of class "poly.mod"
#> Slot "model":
#> [1] "drm"
#>
#> Slot "items":
#> $drm
#> [1] 1 2 3 4 5
#>
#>
#>
#> Slot "common":
#> NULL
#>
#> Slot "location":
#> [1] FALSE
#>
#> Slot "groups":
#> [1] 1
#>
#> Slot "dimensions":
#> [1] 2
#>
plot(plinkpars)
## multidimensional
data <- expand.table(LSAT7)
(mod1 <- mirt(data, 2))
#>
#> Call:
#> mirt(data = data, model = 2)
#>
#> Full-information item factor analysis with 2 factor(s).
#> Converged within 1e-04 tolerance after 436 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: BFGS
#> EM acceleration: Ramsay
#> Number of rectangular quadrature: 31
#> Latent density type: Gaussian
#>
#> Log-likelihood = -2653.52
#> Estimated parameters: 14
#> AIC = 5335.039
#> BIC = 5403.748; SABIC = 5359.283
#> G2 (17) = 21.13, p = 0.2205
#> RMSEA = 0.016, CFI = NaN, TLI = NaN
plinkpars <- read.mirt(mod1)
plinkpars
#> An object of class "irt.pars"
#> Slot "pars":
#> a1 a2
#> [1,] -2.0072336 0.87037703 2.6479635 0
#> [2,] -0.8488425 -0.52210644 0.7876378 0
#> [3,] -2.1530084 -1.83652628 2.4829929 0
#> [4,] -0.7558975 -0.02803433 0.4847282 0
#> [5,] -0.7572717 0.00000000 1.8640953 0
#>
#> Slot "cat":
#> [1] 2 2 2 2 2
#>
#> Slot "poly.mod":
#> An object of class "poly.mod"
#> Slot "model":
#> [1] "drm"
#>
#> Slot "items":
#> $drm
#> [1] 1 2 3 4 5
#>
#>
#>
#> Slot "common":
#> NULL
#>
#> Slot "location":
#> [1] FALSE
#>
#> Slot "groups":
#> [1] 1
#>
#> Slot "dimensions":
#> [1] 2
#>
plot(plinkpars)
 plot(mod1, type = 'trace')
plot(mod1, type = 'trace')
 cmod <- mirt.model('
F1 = 1,4,5
F2 = 2-4')
model <- mirt(data, cmod)
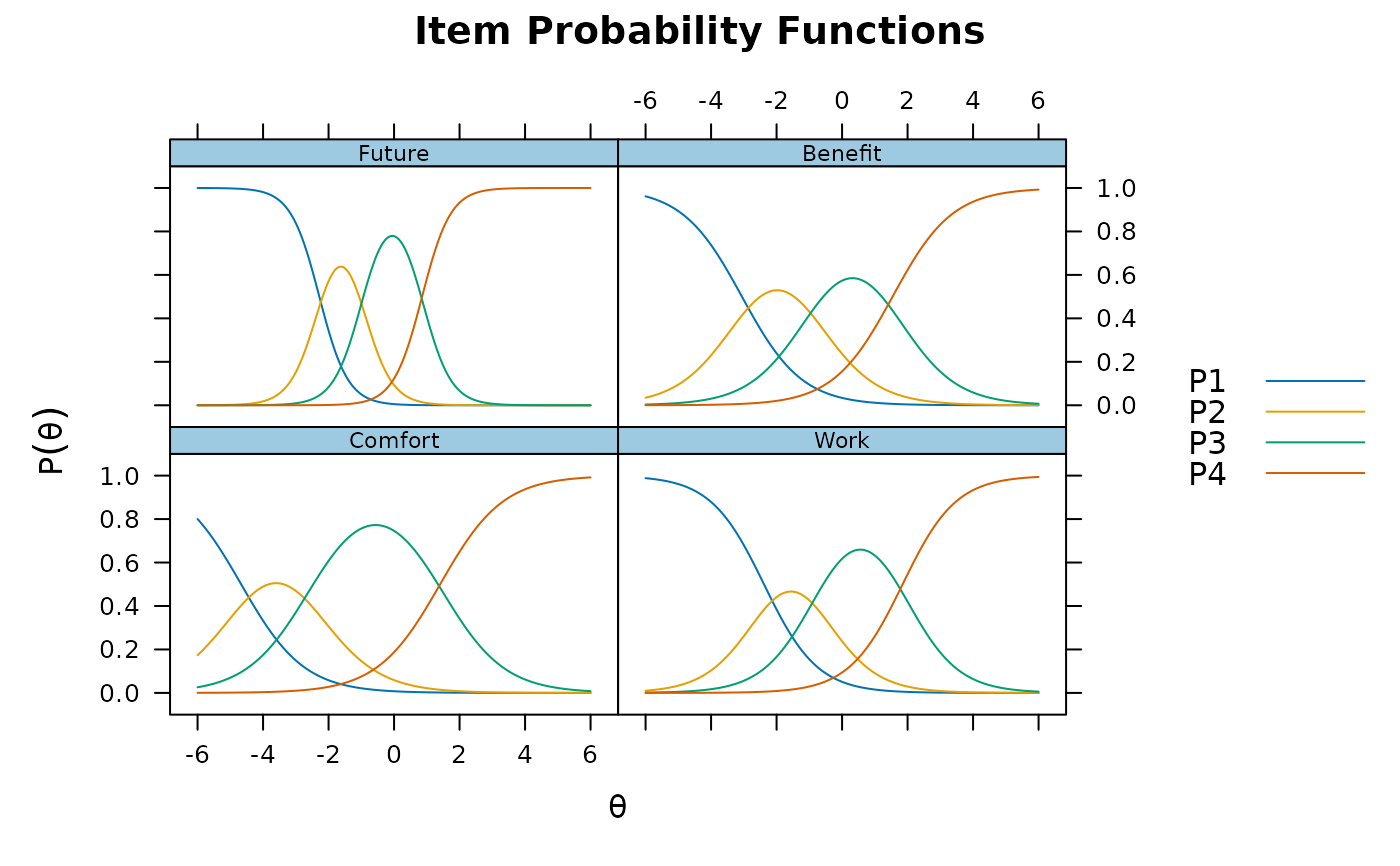
plot(read.mirt(model))
cmod <- mirt.model('
F1 = 1,4,5
F2 = 2-4')
model <- mirt(data, cmod)
plot(read.mirt(model))
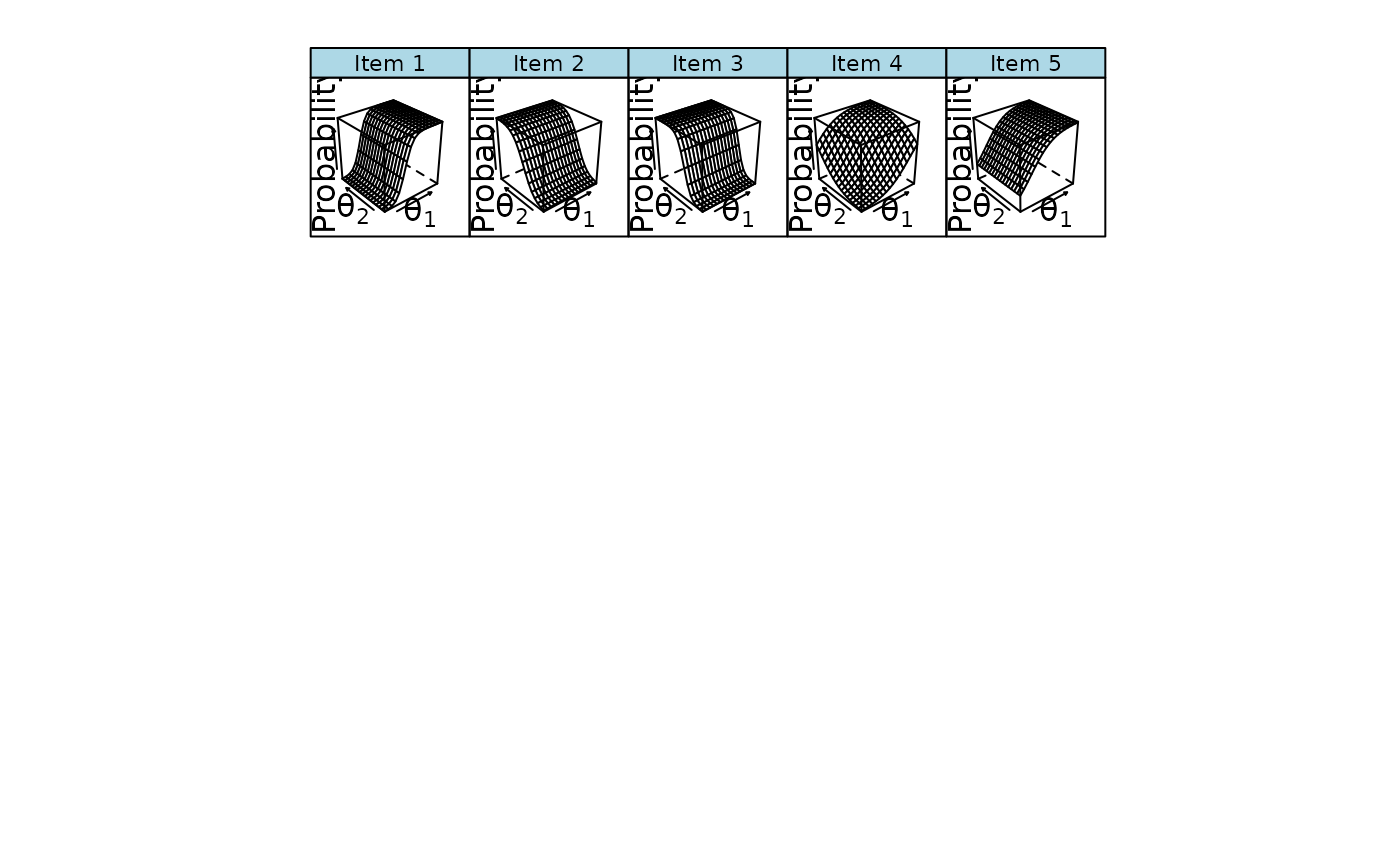 itemplot(model, 1)
itemplot(model, 1)
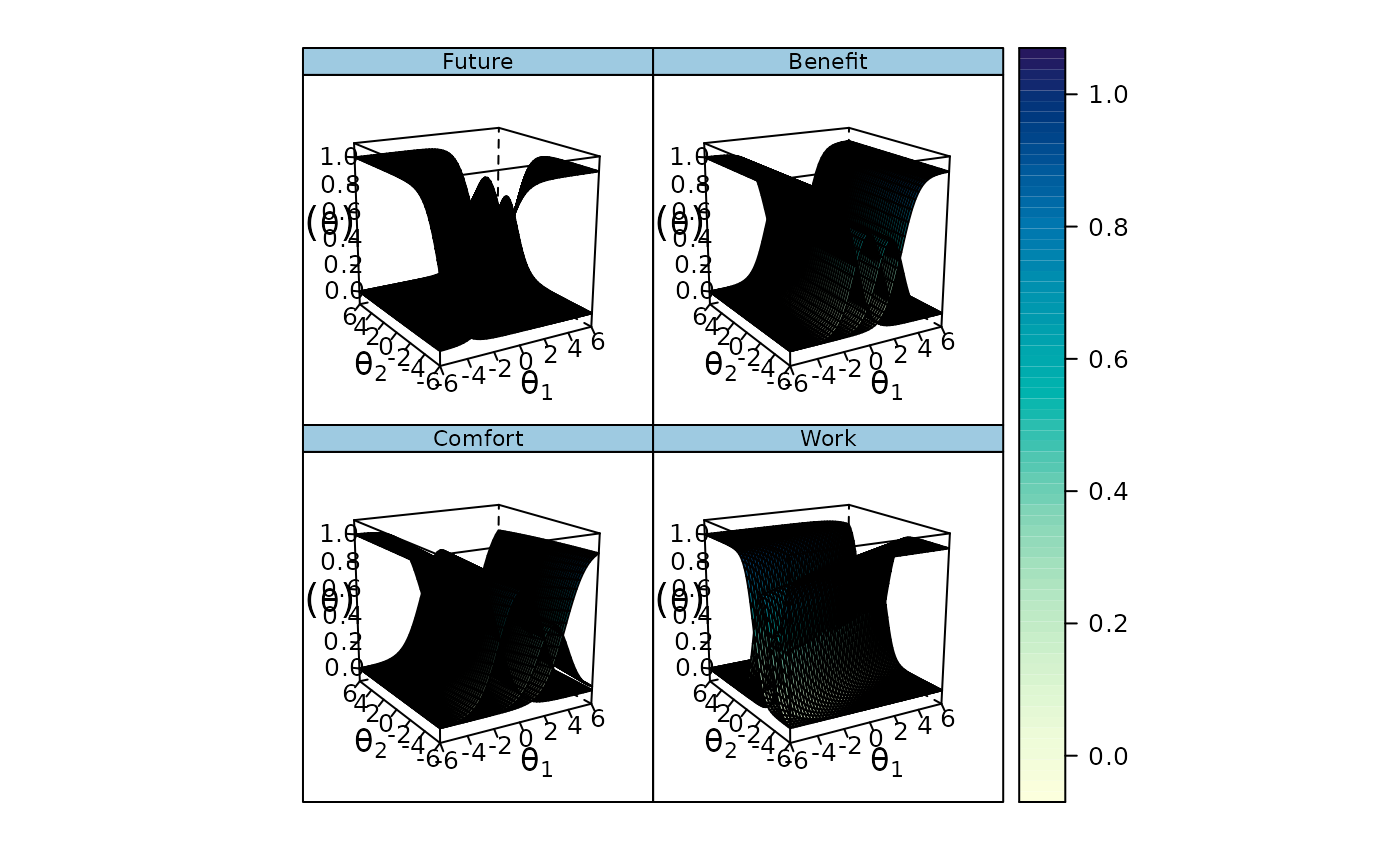
 # graded
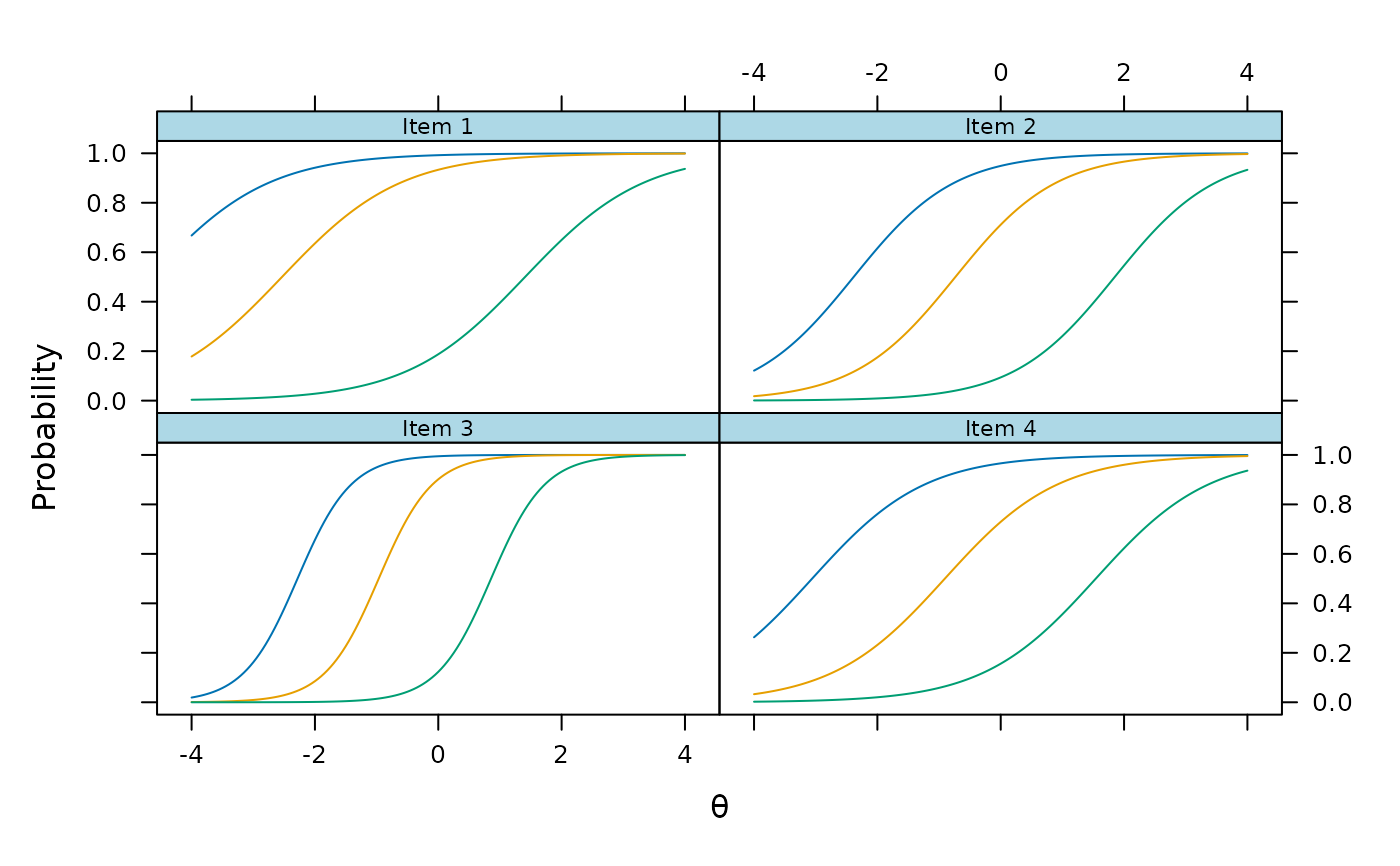
mod2 <- mirt(Science, 2)
plinkpars <- read.mirt(mod2)
plinkpars
#> An object of class "irt.pars"
#> Slot "pars":
#> a1 a2 b1 b2 b3
#> [1,] -1.3350281 0.09676376 5.210669 2.865549 -1.602826
#> [2,] -0.8789508 1.85253465 3.703802 1.153176 -2.904255
#> [3,] -1.4696076 1.16485648 4.663467 1.956626 -1.735796
#> [4,] -1.7220434 0.00000000 3.988789 1.195247 -2.043998
#>
#> Slot "cat":
#> [1] 4 4 4 4
#>
#> Slot "poly.mod":
#> An object of class "poly.mod"
#> Slot "model":
#> [1] "grm"
#>
#> Slot "items":
#> $grm
#> [1] 1 2 3 4
#>
#>
#>
#> Slot "common":
#> NULL
#>
#> Slot "location":
#> [1] FALSE
#>
#> Slot "groups":
#> [1] 1
#>
#> Slot "dimensions":
#> [1] 2
#>
plot(plinkpars)
# graded
mod2 <- mirt(Science, 2)
plinkpars <- read.mirt(mod2)
plinkpars
#> An object of class "irt.pars"
#> Slot "pars":
#> a1 a2 b1 b2 b3
#> [1,] -1.3350281 0.09676376 5.210669 2.865549 -1.602826
#> [2,] -0.8789508 1.85253465 3.703802 1.153176 -2.904255
#> [3,] -1.4696076 1.16485648 4.663467 1.956626 -1.735796
#> [4,] -1.7220434 0.00000000 3.988789 1.195247 -2.043998
#>
#> Slot "cat":
#> [1] 4 4 4 4
#>
#> Slot "poly.mod":
#> An object of class "poly.mod"
#> Slot "model":
#> [1] "grm"
#>
#> Slot "items":
#> $grm
#> [1] 1 2 3 4
#>
#>
#>
#> Slot "common":
#> NULL
#>
#> Slot "location":
#> [1] FALSE
#>
#> Slot "groups":
#> [1] 1
#>
#> Slot "dimensions":
#> [1] 2
#>
plot(plinkpars)
 plot(mod2, type = 'trace')
plot(mod2, type = 'trace')
 ### multiple group equating example
set.seed(1234)
dat <- expand.table(LSAT7)
group <- sample(c('g1', 'g2'), nrow(dat), TRUE)
dat1 <- dat[group == 'g1', ]
dat2 <- dat[group == 'g2', ]
mod1 <- mirt(dat1, 1)
mod2 <- mirt(dat2, 1)
# convert and combine pars
plinkMG <- read.mirt(list(g1=mod1, g2=mod2))
# equivalently:
# mod <- multipleGroup(dat, 1, group)
# plinkMG <- read.mirt(mod)
combine <- matrix(1:5, 5, 2)
comb <- combine.pars(plinkMG, combine, grp.names=unique(group))
out <- plink(comb, rescale="SL")
equate(out)
#> Maximum iterations reached for true score: 0
#> $tse
#> theta g2 g1
#> 1 -160.732949 0 0.000000
#> 2 -3.233741 1 0.973481
#> 3 -1.910192 2 2.023409
#> 4 -0.999050 3 3.021848
#> 5 0.048359 4 3.973672
#> 6 57.337797 5 5.000000
#>
#> $ose
#> $ose$scores
#> eap.theta.g2 eap.sd.g2 g2 g1
#> 1 -1.896444 0.698843 0 0.0000000
#> 2 -1.474472 0.697610 1 0.9893317
#> 3 -1.002953 0.716007 2 1.9956600
#> 4 -0.455590 0.747730 3 2.9912425
#> 5 0.123384 0.782773 4 3.9901784
#> 6 0.678747 0.812793 5 4.9949444
#>
#> $ose$dist
#> $ose$dist$g2
#> score pop1 pop2 syn
#> [1,] 0 0.03273187 0.03273187 0.03273187
#> [2,] 1 0.17343742 0.17343742 0.17343742
#> [3,] 2 0.48733074 0.48733074 0.48733074
#> [4,] 3 0.99873451 0.99873451 0.99873451
#> [5,] 4 1.61799716 1.61799716 1.61799716
#> [6,] 5 1.56457520 1.56457520 1.56457520
#>
#> $ose$dist$g1
#> score pop1 pop2 syn
#> [1,] 0 0.0338755 0.0338755 0.0338755
#> [2,] 1 0.1748815 0.1748815 0.1748815
#> [3,] 2 0.4863770 0.4863770 0.4863770
#> [4,] 3 1.0132130 1.0132130 1.0132130
#> [5,] 4 1.6175460 1.6175460 1.6175460
#> [6,] 5 1.5489139 1.5489139 1.5489139
#>
#>
#>
equate(out, method = 'OSE')
#> $scores
#> eap.theta.g2 eap.sd.g2 g2 g1
#> 1 -1.896444 0.698843 0 0.0000000
#> 2 -1.474472 0.697610 1 0.9893317
#> 3 -1.002953 0.716007 2 1.9956600
#> 4 -0.455590 0.747730 3 2.9912425
#> 5 0.123384 0.782773 4 3.9901784
#> 6 0.678747 0.812793 5 4.9949444
#>
#> $dist
#> $dist$g2
#> score pop1 pop2 syn
#> [1,] 0 0.03273187 0.03273187 0.03273187
#> [2,] 1 0.17343742 0.17343742 0.17343742
#> [3,] 2 0.48733074 0.48733074 0.48733074
#> [4,] 3 0.99873451 0.99873451 0.99873451
#> [5,] 4 1.61799716 1.61799716 1.61799716
#> [6,] 5 1.56457520 1.56457520 1.56457520
#>
#> $dist$g1
#> score pop1 pop2 syn
#> [1,] 0 0.0338755 0.0338755 0.0338755
#> [2,] 1 0.1748815 0.1748815 0.1748815
#> [3,] 2 0.4863770 0.4863770 0.4863770
#> [4,] 3 1.0132130 1.0132130 1.0132130
#> [5,] 4 1.6175460 1.6175460 1.6175460
#> [6,] 5 1.5489139 1.5489139 1.5489139
#>
#>
# }
### multiple group equating example
set.seed(1234)
dat <- expand.table(LSAT7)
group <- sample(c('g1', 'g2'), nrow(dat), TRUE)
dat1 <- dat[group == 'g1', ]
dat2 <- dat[group == 'g2', ]
mod1 <- mirt(dat1, 1)
mod2 <- mirt(dat2, 1)
# convert and combine pars
plinkMG <- read.mirt(list(g1=mod1, g2=mod2))
# equivalently:
# mod <- multipleGroup(dat, 1, group)
# plinkMG <- read.mirt(mod)
combine <- matrix(1:5, 5, 2)
comb <- combine.pars(plinkMG, combine, grp.names=unique(group))
out <- plink(comb, rescale="SL")
equate(out)
#> Maximum iterations reached for true score: 0
#> $tse
#> theta g2 g1
#> 1 -160.732949 0 0.000000
#> 2 -3.233741 1 0.973481
#> 3 -1.910192 2 2.023409
#> 4 -0.999050 3 3.021848
#> 5 0.048359 4 3.973672
#> 6 57.337797 5 5.000000
#>
#> $ose
#> $ose$scores
#> eap.theta.g2 eap.sd.g2 g2 g1
#> 1 -1.896444 0.698843 0 0.0000000
#> 2 -1.474472 0.697610 1 0.9893317
#> 3 -1.002953 0.716007 2 1.9956600
#> 4 -0.455590 0.747730 3 2.9912425
#> 5 0.123384 0.782773 4 3.9901784
#> 6 0.678747 0.812793 5 4.9949444
#>
#> $ose$dist
#> $ose$dist$g2
#> score pop1 pop2 syn
#> [1,] 0 0.03273187 0.03273187 0.03273187
#> [2,] 1 0.17343742 0.17343742 0.17343742
#> [3,] 2 0.48733074 0.48733074 0.48733074
#> [4,] 3 0.99873451 0.99873451 0.99873451
#> [5,] 4 1.61799716 1.61799716 1.61799716
#> [6,] 5 1.56457520 1.56457520 1.56457520
#>
#> $ose$dist$g1
#> score pop1 pop2 syn
#> [1,] 0 0.0338755 0.0338755 0.0338755
#> [2,] 1 0.1748815 0.1748815 0.1748815
#> [3,] 2 0.4863770 0.4863770 0.4863770
#> [4,] 3 1.0132130 1.0132130 1.0132130
#> [5,] 4 1.6175460 1.6175460 1.6175460
#> [6,] 5 1.5489139 1.5489139 1.5489139
#>
#>
#>
equate(out, method = 'OSE')
#> $scores
#> eap.theta.g2 eap.sd.g2 g2 g1
#> 1 -1.896444 0.698843 0 0.0000000
#> 2 -1.474472 0.697610 1 0.9893317
#> 3 -1.002953 0.716007 2 1.9956600
#> 4 -0.455590 0.747730 3 2.9912425
#> 5 0.123384 0.782773 4 3.9901784
#> 6 0.678747 0.812793 5 4.9949444
#>
#> $dist
#> $dist$g2
#> score pop1 pop2 syn
#> [1,] 0 0.03273187 0.03273187 0.03273187
#> [2,] 1 0.17343742 0.17343742 0.17343742
#> [3,] 2 0.48733074 0.48733074 0.48733074
#> [4,] 3 0.99873451 0.99873451 0.99873451
#> [5,] 4 1.61799716 1.61799716 1.61799716
#> [6,] 5 1.56457520 1.56457520 1.56457520
#>
#> $dist$g1
#> score pop1 pop2 syn
#> [1,] 0 0.0338755 0.0338755 0.0338755
#> [2,] 1 0.1748815 0.1748815 0.1748815
#> [3,] 2 0.4863770 0.4863770 0.4863770
#> [4,] 3 1.0132130 1.0132130 1.0132130
#> [5,] 4 1.6175460 1.6175460 1.6175460
#> [6,] 5 1.5489139 1.5489139 1.5489139
#>
#>
# }