Skip to contents

Plot various test-implied functions from models

Source: R/MultipleGroup-methods.R, R/SingleGroup-methods.R
plot-method.Rd

Plot various test implied response functions from models estimated in the mirt package.

Usage

# S4 method for class 'MultipleGroupClass,missing'
plot(
  x,
  y,
  type = "score",
  npts = 200,
  drop2 = TRUE,
  degrees = 45,
  which.items = 1:extract.mirt(x, "nitems"),
  rot = list(xaxis = -70, yaxis = 30, zaxis = 10),
  facet_items = TRUE,
  theta_lim = c(-6, 6),
  par.strip.text = list(cex = 0.7),
  par.settings = list(strip.background = list(col = "#9ECAE1"), strip.border = list(col =
    "black")),
  auto.key = list(space = "right", points = FALSE, lines = TRUE),
  ...
)

# S4 method for class 'SingleGroupClass,missing'
plot(
  x,
  y,
  type = "score",
  npts = 200,
  drop2 = TRUE,
  degrees = 45,
  theta_lim = c(-6, 6),
  which.items = 1:extract.mirt(x, "nitems"),
  MI = 0,
  CI = 0.95,
  rot = list(xaxis = -70, yaxis = 30, zaxis = 10),
  facet_items = TRUE,
  main = NULL,
  drape = TRUE,
  colorkey = TRUE,
  ehist.cut = 1e-10,
  add.ylab2 = TRUE,
  par.strip.text = list(cex = 0.7),
  par.settings = list(strip.background = list(col = "#9ECAE1"), strip.border = list(col =
    "black")),
  auto.key = list(space = "right", points = FALSE, lines = TRUE),
  profile = FALSE,
  ...
)

Arguments

x

an object of class SingleGroupClass, MultipleGroupClass, or DiscreteClass

y

an arbitrary missing argument required for R CMD check

type

type of plot to view. Can be

'info'

test information function

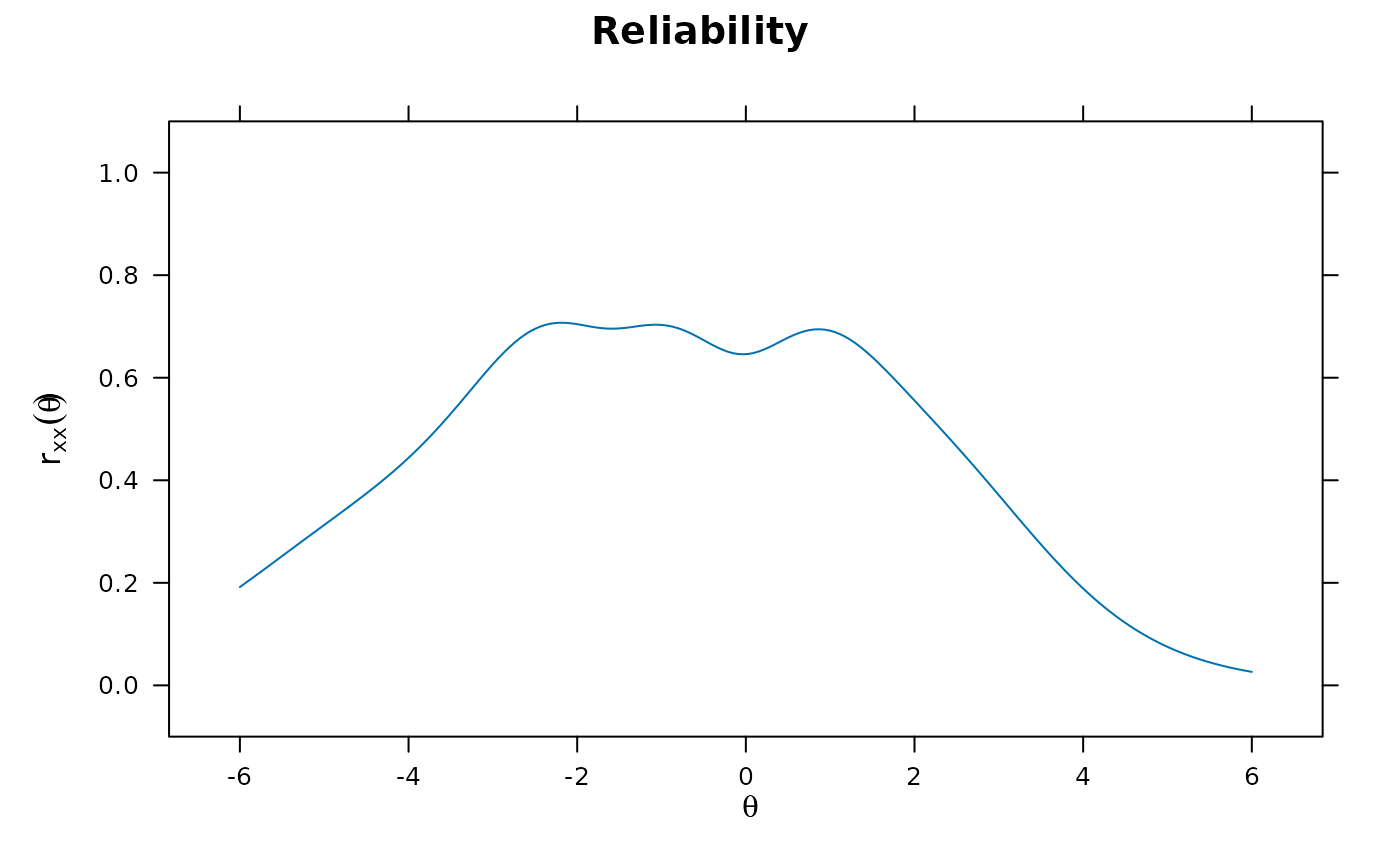
'rxx'

for the reliability function

'infocontour'

for the test information contours

'SE'

for the test standard error function

'infotrace'

item information traceline plots

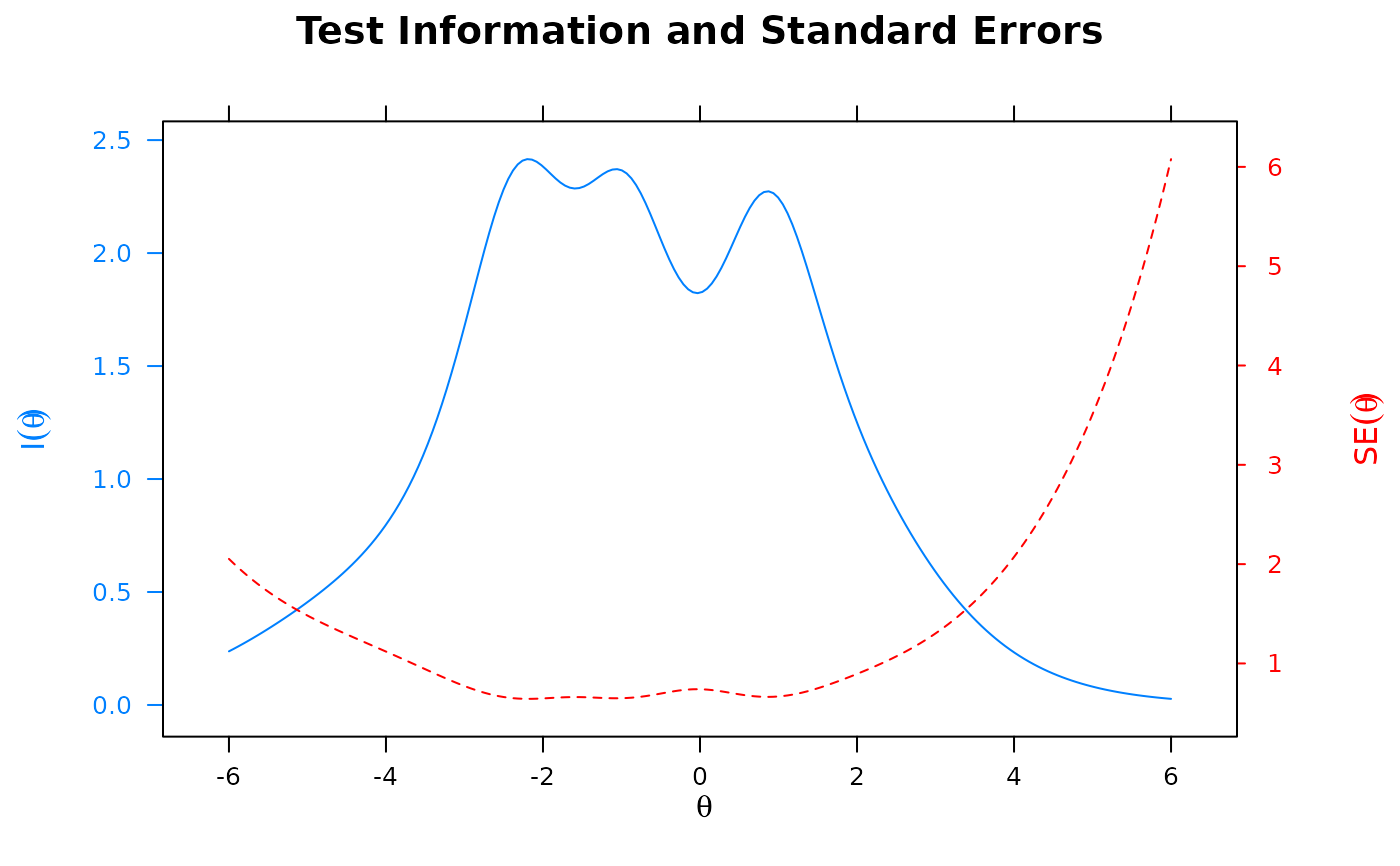
'infoSE'

a combined test information and standard error plot

'trace'

item probability traceline plots

'itemscore'

item scoring traceline plots

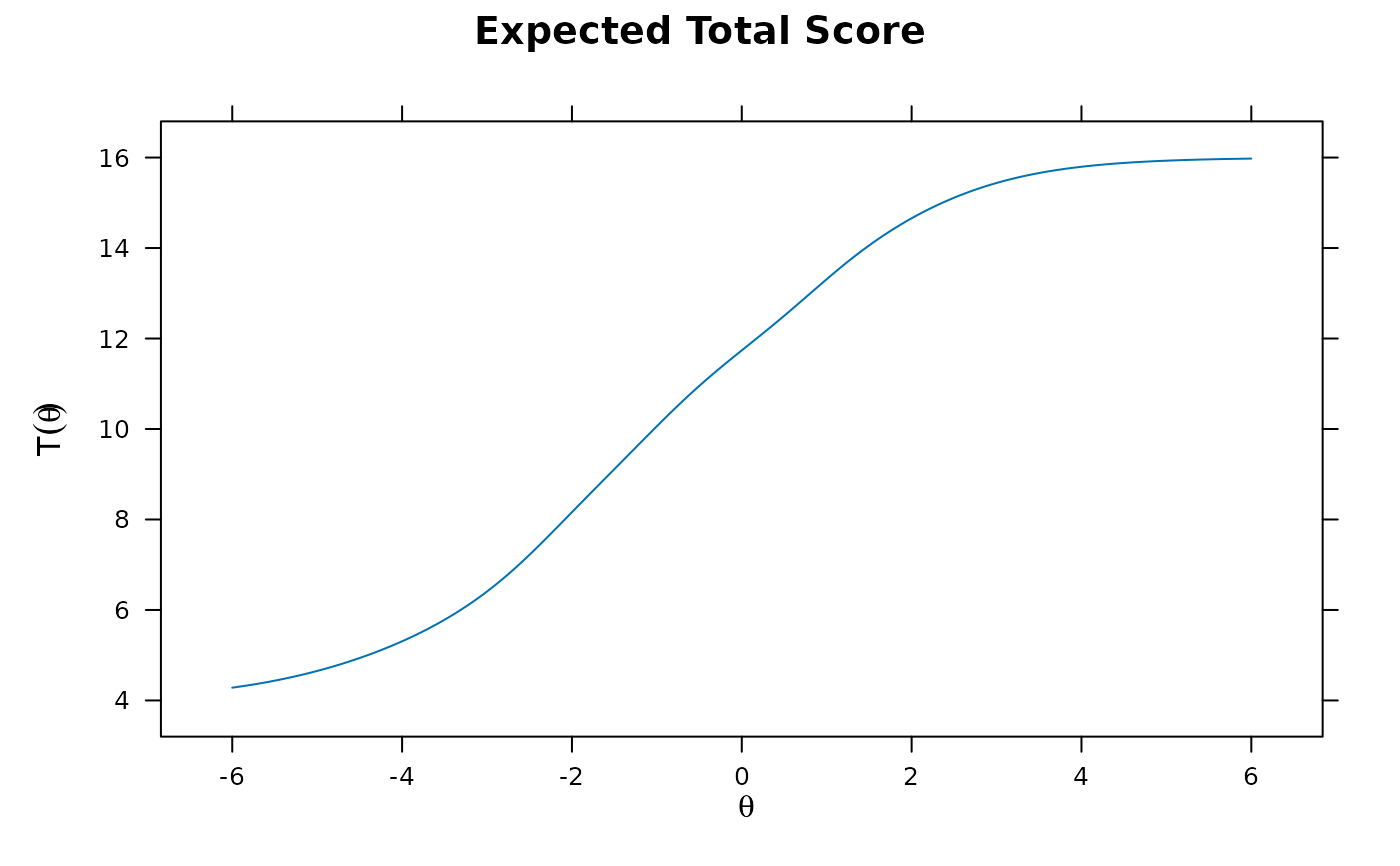
'score'

expected total score surface

'scorecontour'

expected total score contour plot

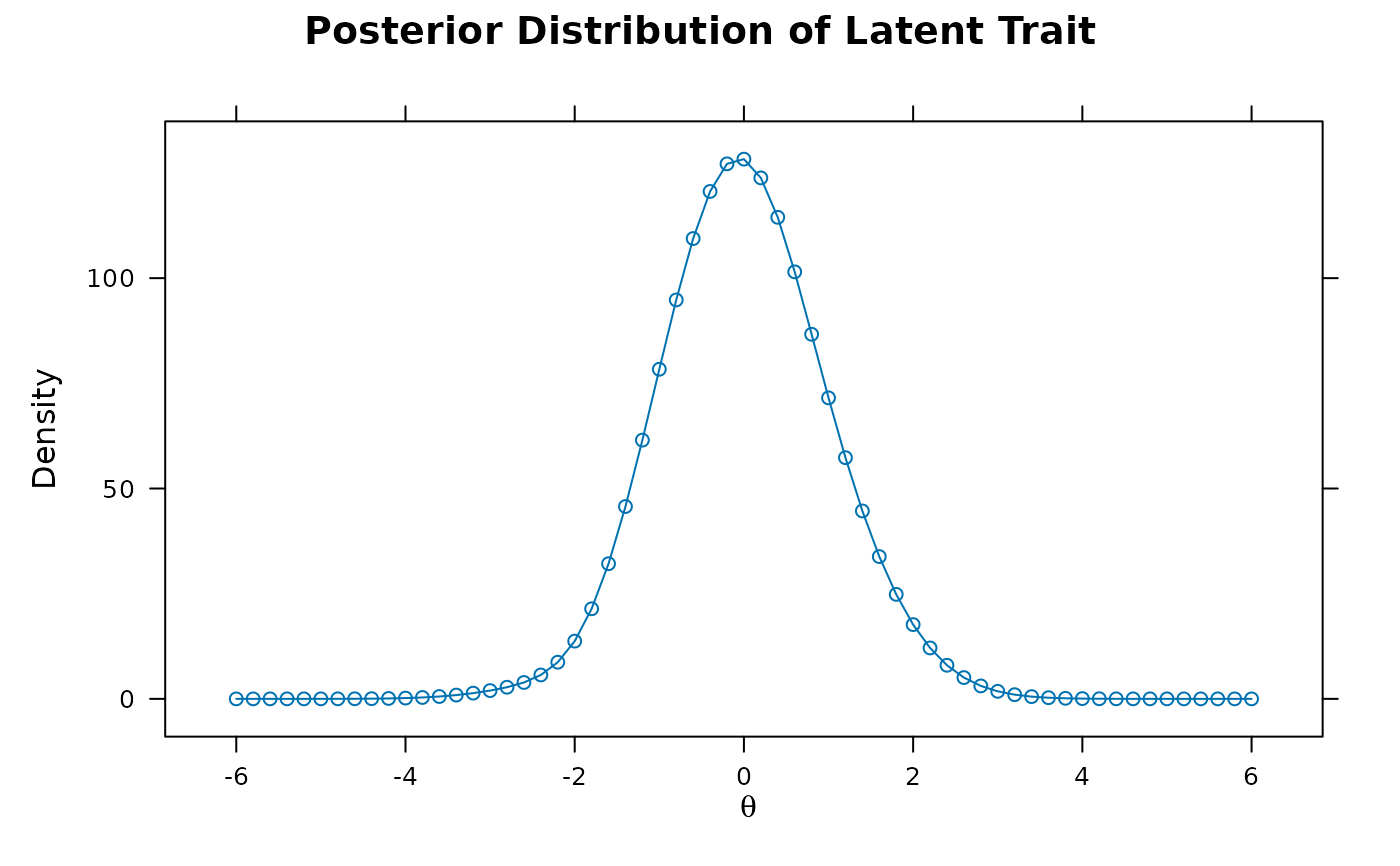
'posteriorTheta'

posterior for the latent trait distribution

'EAPsum'

compares sum-scores to the expected values based on the EAP for sum-scores method (see fscores)

Note that if dentype = 'empiricalhist' was used in estimation then the type 'empiricalhist' also will be available to generate the empirical histogram plot, and if dentype = 'Davidian-#' was used then the type 'Davidian' will also be available to generate the curve estimates at the quadrature nodes used during estimation

npts

number of quadrature points to be used for plotting features. Larger values make plots look smoother

drop2

logical; where appropriate, for dichotomous response items drop the lowest category and provide information pertaining only to the second response option?

degrees

numeric value ranging from 0 to 90 used in plot to compute angle for information-based plots with respect to the first dimension. If a vector is used then a bubble plot is created with the summed information across the angles specified (e.g., degrees = seq(0, 90, by=10))

which.items

numeric vector indicating which items to be used when plotting. Default is to use all available items

rot

allows rotation of the 3D graphics

facet_items

logical; apply grid of plots across items? If FALSE, items will be placed in one plot for each group

theta_lim

lower and upper limits of the latent trait (theta) to be evaluated, and is used in conjunction with npts

par.strip.text

plotting argument passed to lattice

par.settings

plotting argument passed to lattice

auto.key

plotting argument passed to lattice

...

additional arguments to be passed to lattice

MI

a single number indicating how many imputations to draw to form bootstrapped confidence intervals for the selected test statistic. If greater than 0 a plot will be drawn with a shaded region for the interval

CI

a number from 0 to 1 indicating the confidence interval to select when MI input is used. Default uses the 95% confidence (CI = .95)

main

argument passed to lattice. Default generated automatically

drape

logical argument passed to lattice. Default generated automatically

colorkey

logical argument passed to lattice. Default generated automatically

ehist.cut

a probability value indicating a threshold for excluding cases in empirical histogram plots. Values larger than the default will include more points in the tails of the plot, potentially squishing the 'meat' of the plot to take up less area than visually desired

add.ylab2

logical argument passed to lattice. Default generated automatically

profile

logical; provide a profile plot of response probabilities (objects returned from mdirt only)

References

Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06

Examples


# \donttest{
x <- mirt(Science, 1, SE=TRUE)
#> 
Iteration: 1, Log-Lik: -1629.361, Max-Change: 0.50660
Iteration: 2, Log-Lik: -1617.374, Max-Change: 0.25442
Iteration: 3, Log-Lik: -1612.894, Max-Change: 0.16991
Iteration: 4, Log-Lik: -1610.306, Max-Change: 0.10461
Iteration: 5, Log-Lik: -1609.814, Max-Change: 0.09162
Iteration: 6, Log-Lik: -1609.534, Max-Change: 0.07363
Iteration: 7, Log-Lik: -1609.030, Max-Change: 0.03677
Iteration: 8, Log-Lik: -1608.988, Max-Change: 0.03200
Iteration: 9, Log-Lik: -1608.958, Max-Change: 0.02754
Iteration: 10, Log-Lik: -1608.878, Max-Change: 0.01443
Iteration: 11, Log-Lik: -1608.875, Max-Change: 0.00847
Iteration: 12, Log-Lik: -1608.873, Max-Change: 0.00515
Iteration: 13, Log-Lik: -1608.872, Max-Change: 0.00550
Iteration: 14, Log-Lik: -1608.872, Max-Change: 0.00318
Iteration: 15, Log-Lik: -1608.871, Max-Change: 0.00462
Iteration: 16, Log-Lik: -1608.871, Max-Change: 0.00277
Iteration: 17, Log-Lik: -1608.870, Max-Change: 0.00145
Iteration: 18, Log-Lik: -1608.870, Max-Change: 0.00175
Iteration: 19, Log-Lik: -1608.870, Max-Change: 0.00126
Iteration: 20, Log-Lik: -1608.870, Max-Change: 0.00025
Iteration: 21, Log-Lik: -1608.870, Max-Change: 0.00285
Iteration: 22, Log-Lik: -1608.870, Max-Change: 0.00108
Iteration: 23, Log-Lik: -1608.870, Max-Change: 0.00022
Iteration: 24, Log-Lik: -1608.870, Max-Change: 0.00059
Iteration: 25, Log-Lik: -1608.870, Max-Change: 0.00014
Iteration: 26, Log-Lik: -1608.870, Max-Change: 0.00068
Iteration: 27, Log-Lik: -1608.870, Max-Change: 0.00065
Iteration: 28, Log-Lik: -1608.870, Max-Change: 0.00019
Iteration: 29, Log-Lik: -1608.870, Max-Change: 0.00061
Iteration: 30, Log-Lik: -1608.870, Max-Change: 0.00012
Iteration: 31, Log-Lik: -1608.870, Max-Change: 0.00012
Iteration: 32, Log-Lik: -1608.870, Max-Change: 0.00058
Iteration: 33, Log-Lik: -1608.870, Max-Change: 0.00055
Iteration: 34, Log-Lik: -1608.870, Max-Change: 0.00015
Iteration: 35, Log-Lik: -1608.870, Max-Change: 0.00052
Iteration: 36, Log-Lik: -1608.870, Max-Change: 0.00010
#> 
#> Calculating information matrix...
plot(x)

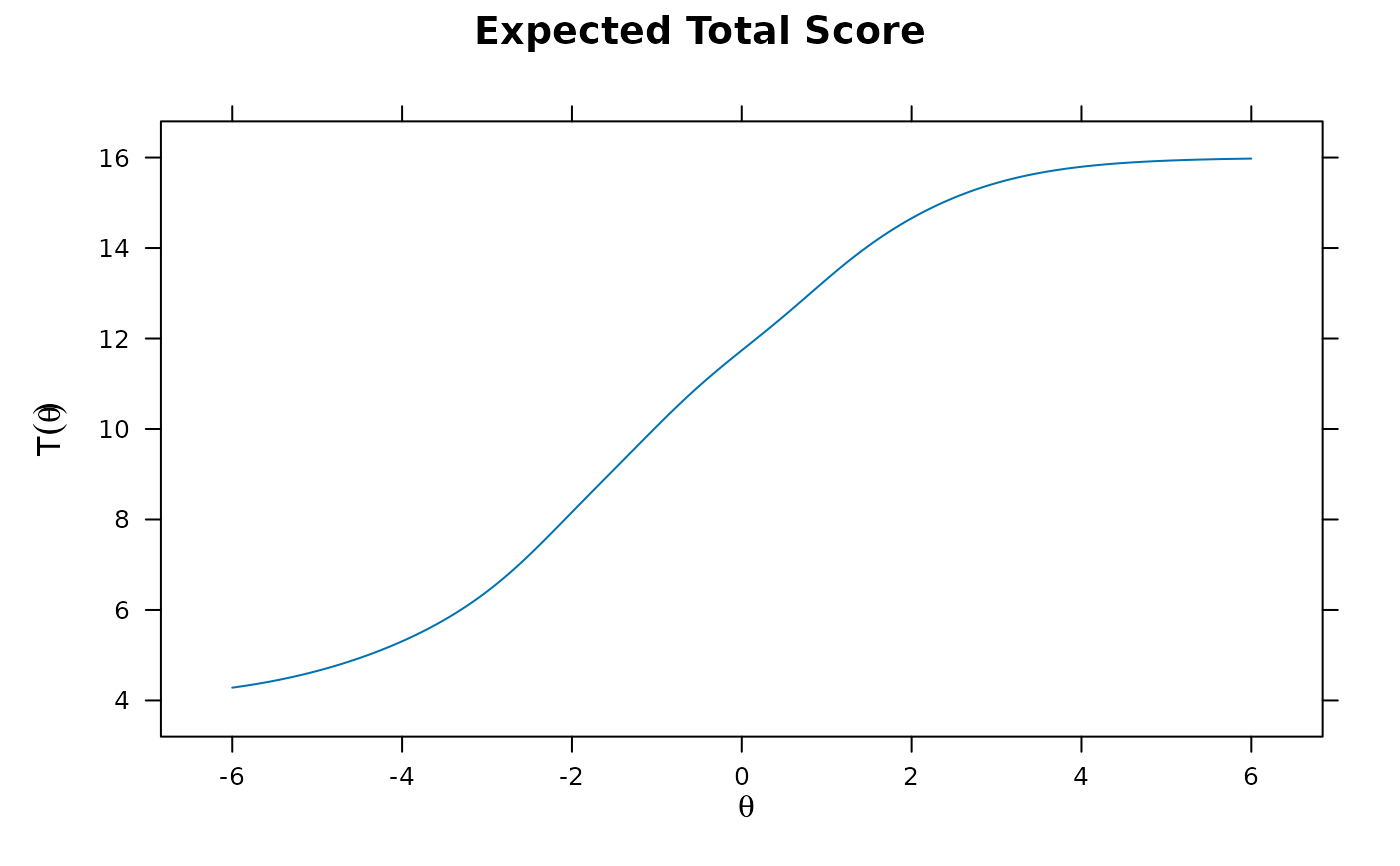plot(x, type = 'info')

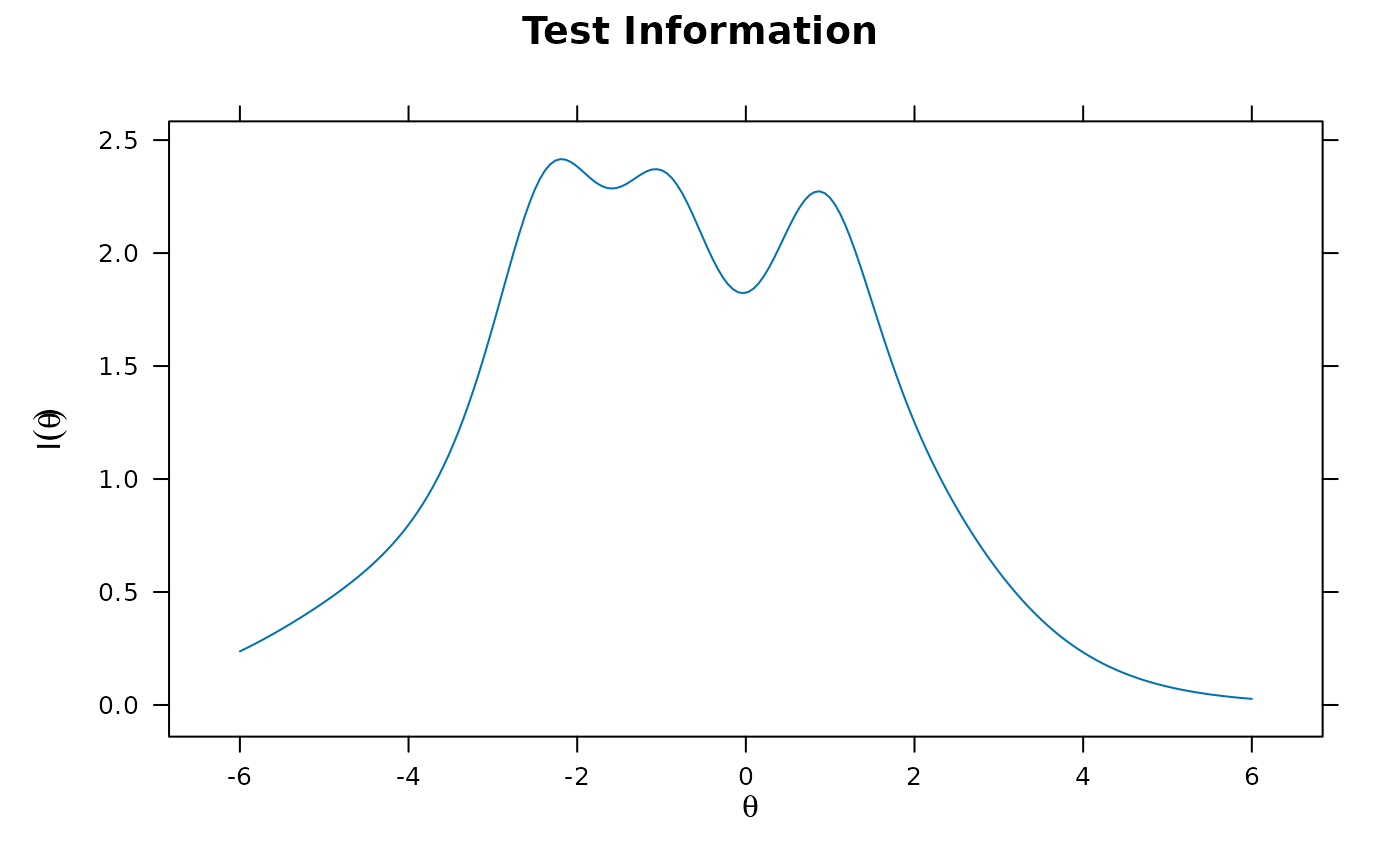plot(x, type = 'infotrace')

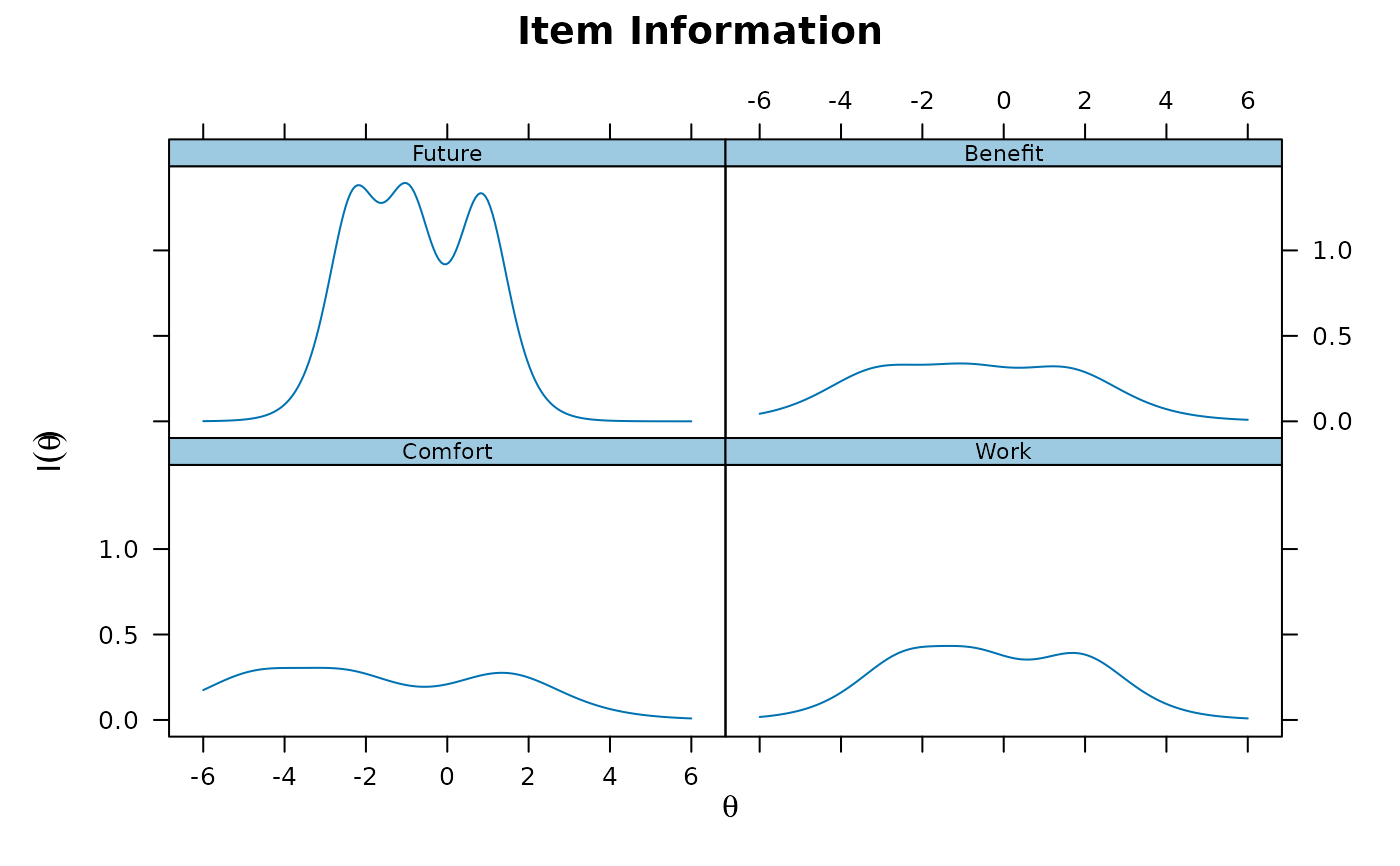plot(x, type = 'infotrace', facet_items = FALSE)

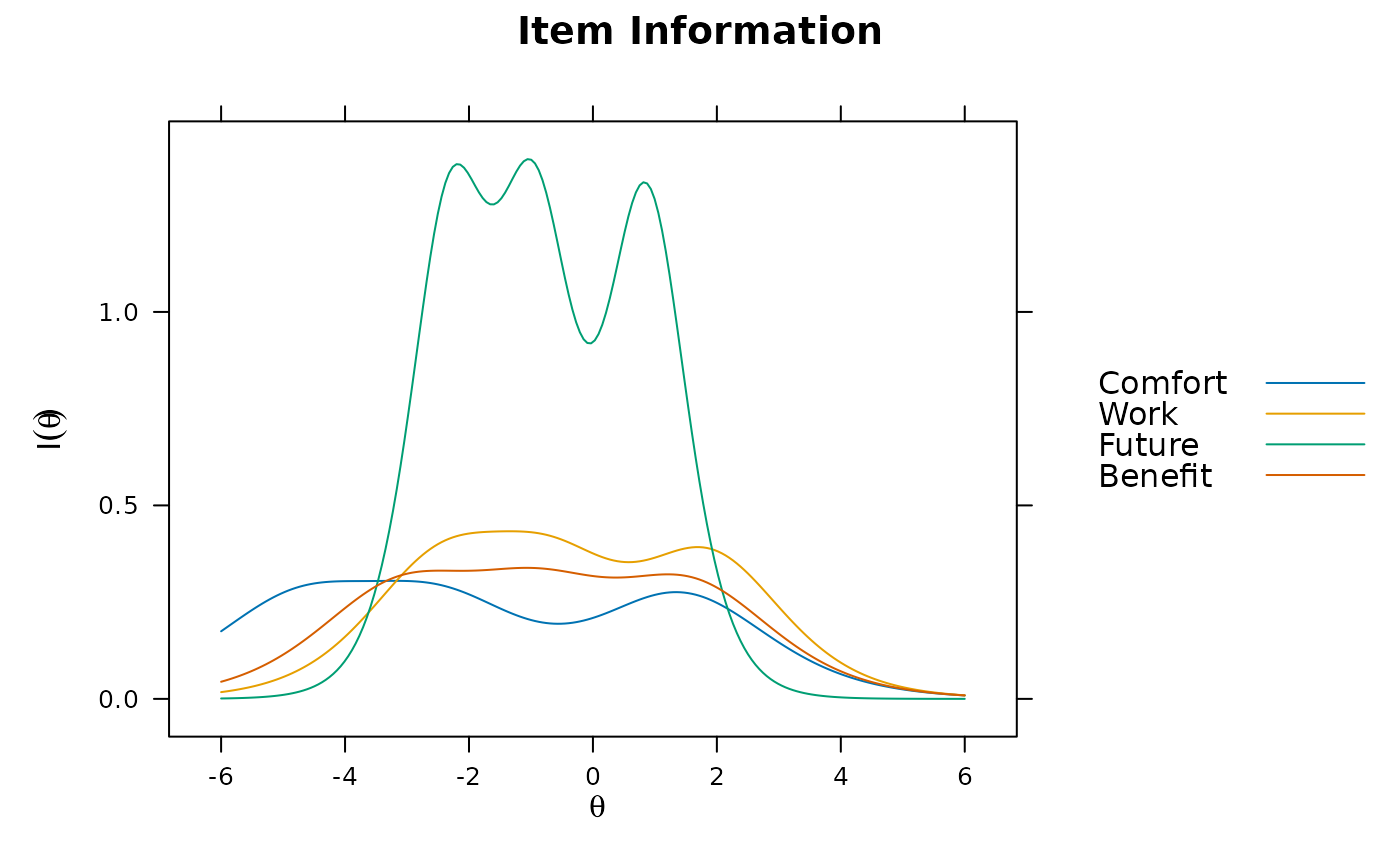plot(x, type = 'infoSE')

plot(x, type = 'rxx')

plot(x, type = 'posteriorTheta')


# confidence interval plots when information matrix computed
plot(x)

plot(x, MI=100)

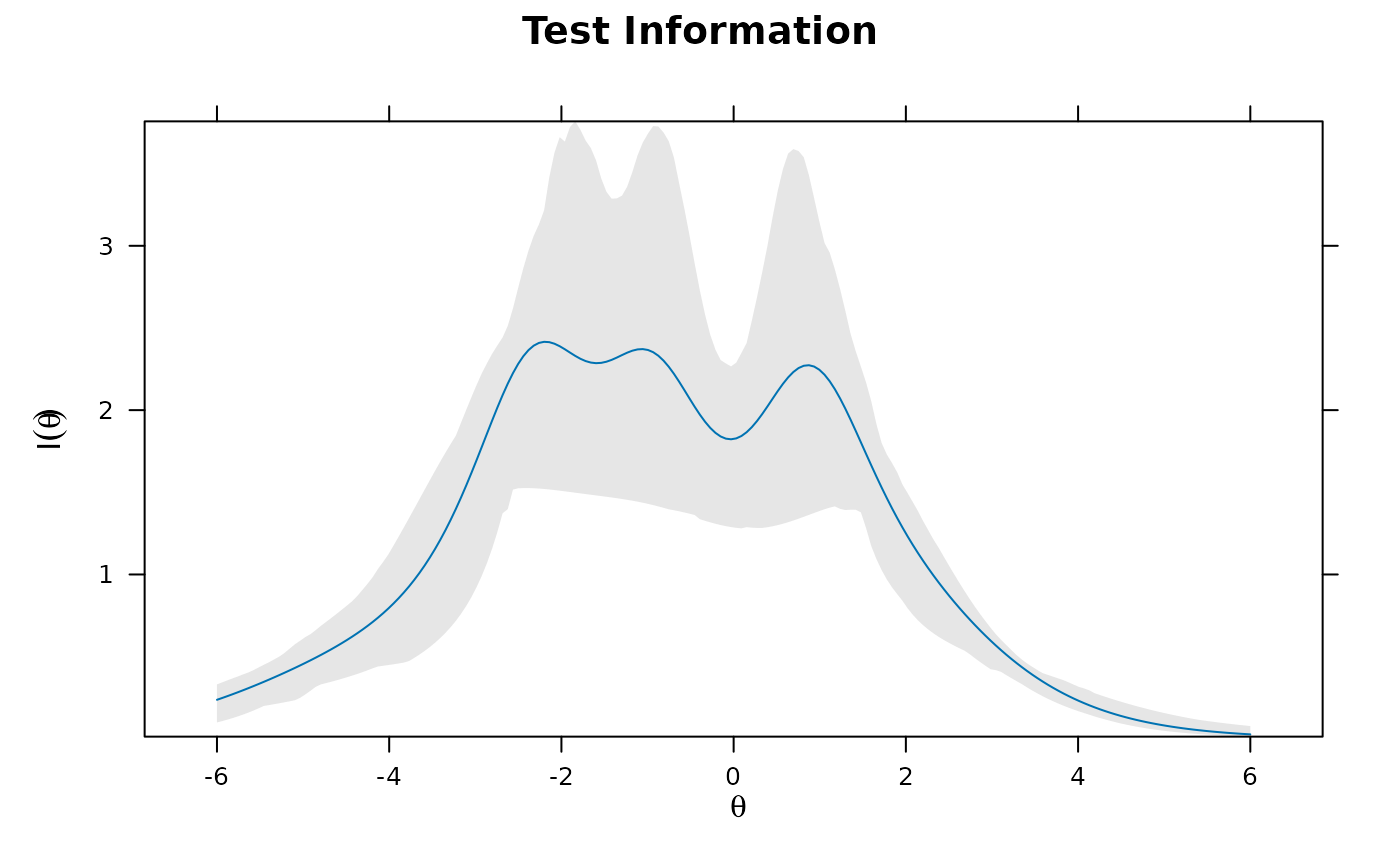plot(x, type='info', MI=100)

plot(x, type='SE', MI=100)

plot(x, type='rxx', MI=100)


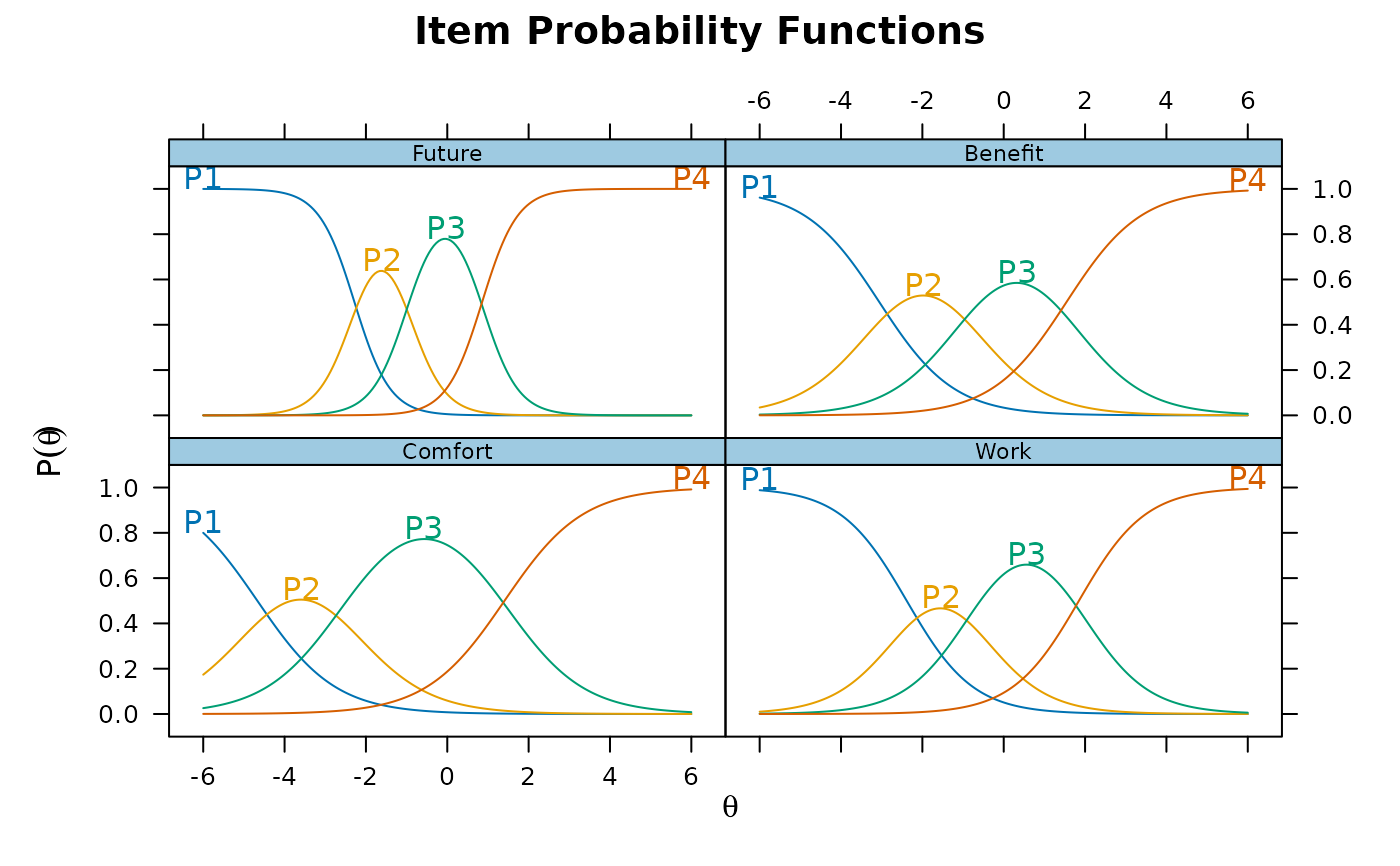# use the directlabels package to put labels on tracelines
library(directlabels)
plt <- plot(x, type = 'trace')
direct.label(plt, 'top.points')


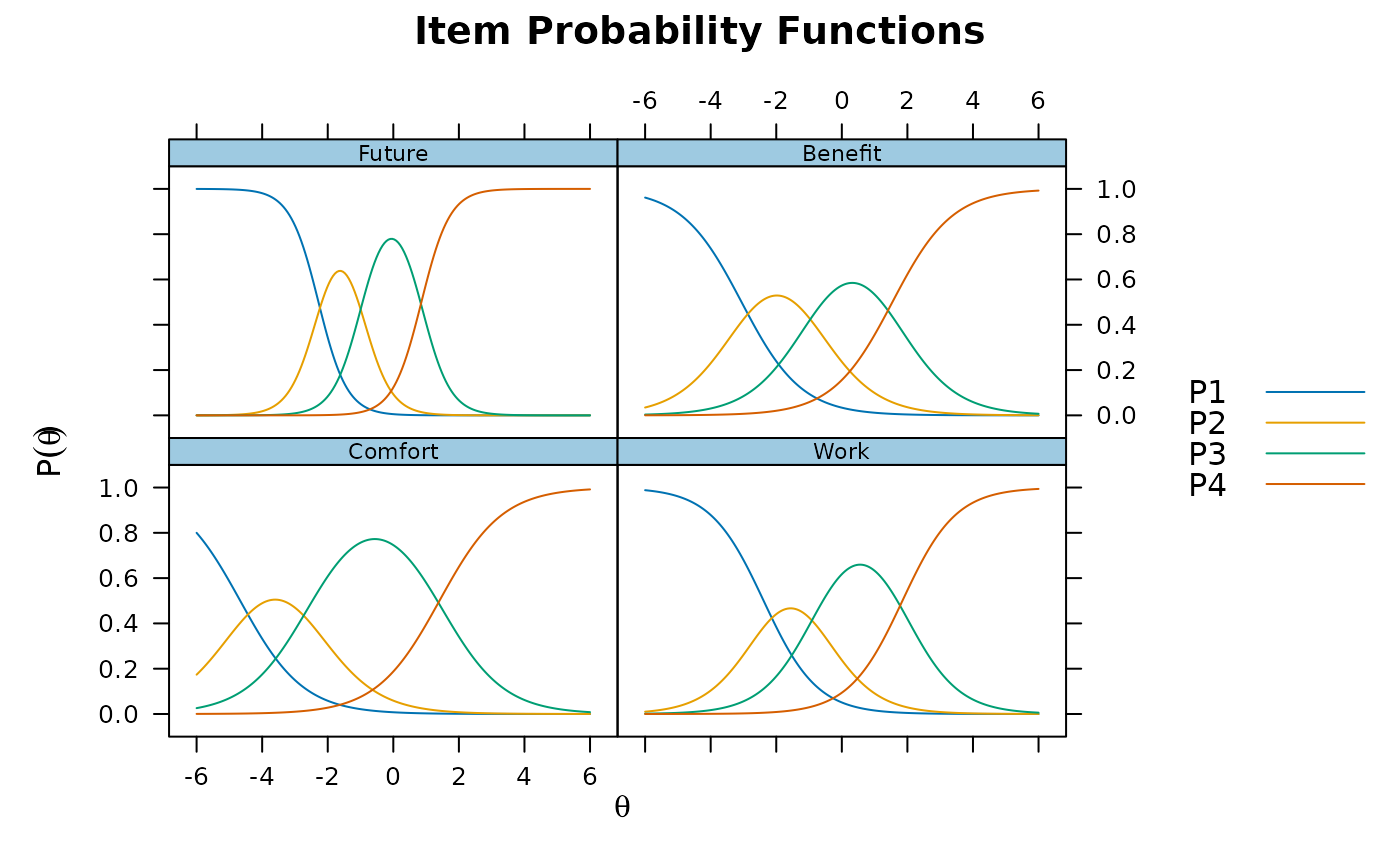# additional modifications can be made via update().
# See ?update.trellis for further documentation
plt

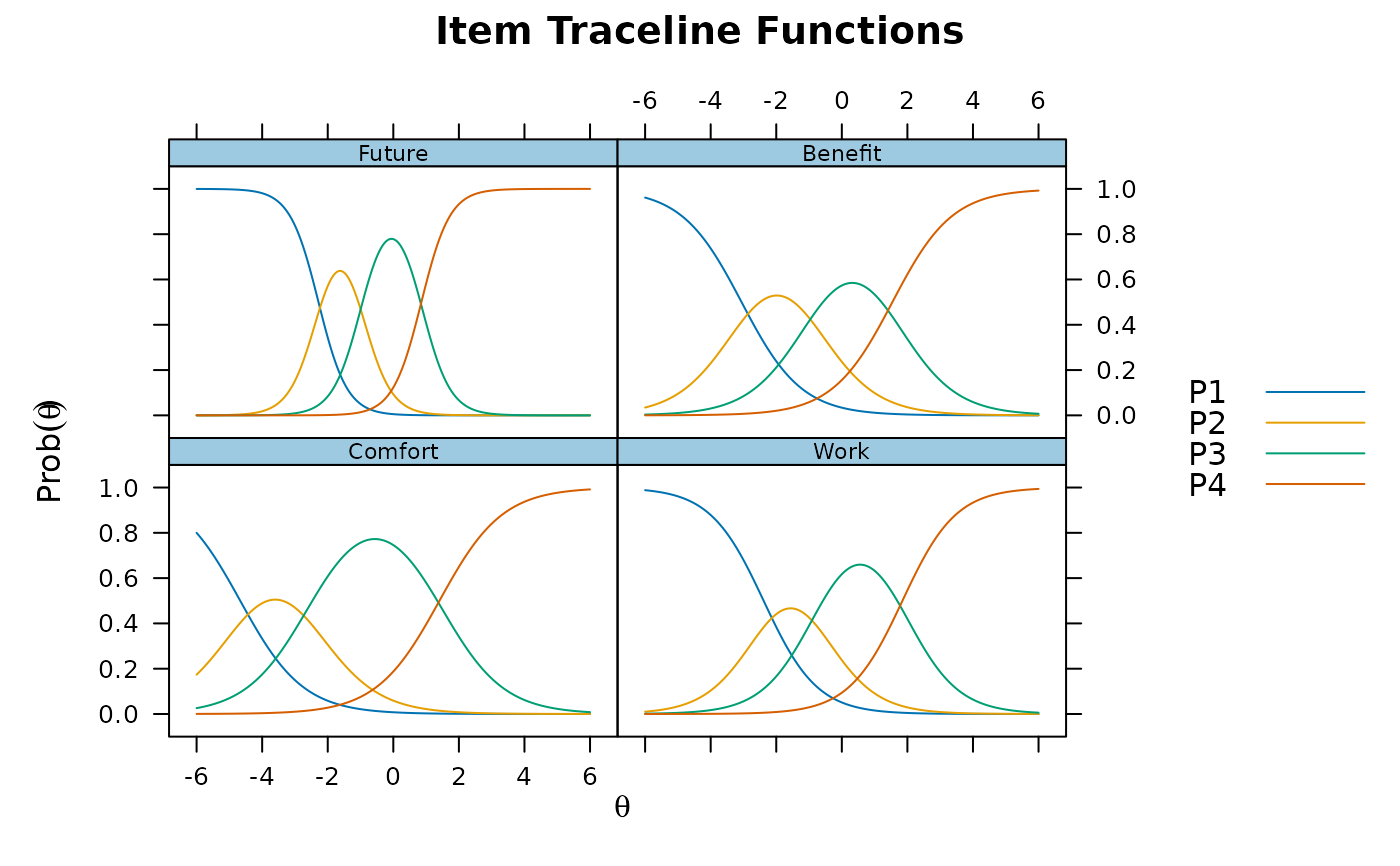update(plt, ylab = expression(Prob(theta)),
            main = "Item Traceline Functions") # ylab/main changed


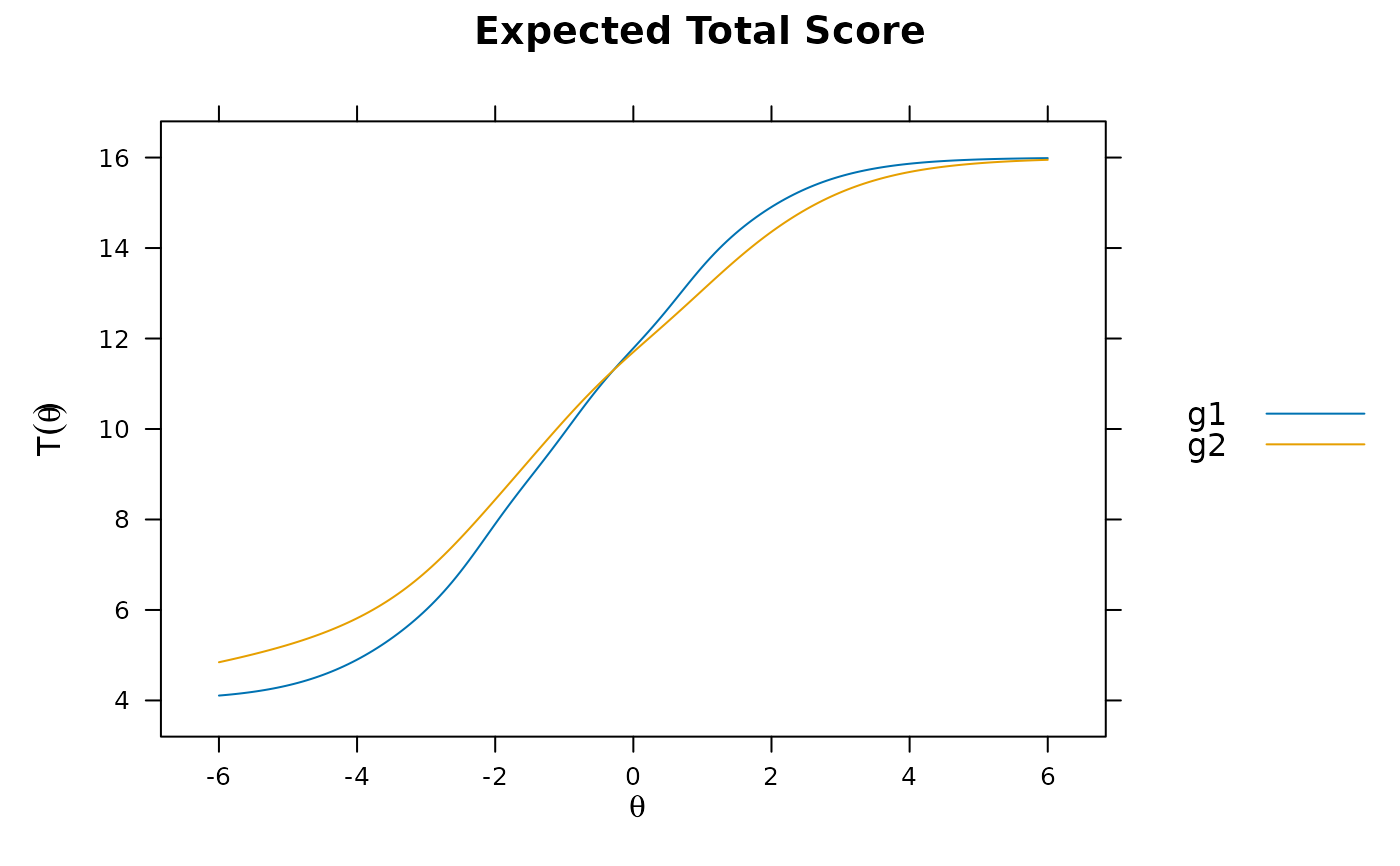set.seed(1234)
group <- sample(c('g1','g2'), nrow(Science), TRUE)
x2 <- multipleGroup(Science, 1, group)
#> 
Iteration: 1, Log-Lik: -1629.361, Max-Change: 1.26522
Iteration: 2, Log-Lik: -1610.754, Max-Change: 0.35318
Iteration: 3, Log-Lik: -1605.815, Max-Change: 0.27496
Iteration: 4, Log-Lik: -1603.729, Max-Change: 0.26576
Iteration: 5, Log-Lik: -1602.689, Max-Change: 0.16338
Iteration: 6, Log-Lik: -1602.161, Max-Change: 0.13792
Iteration: 7, Log-Lik: -1601.411, Max-Change: 0.07441
Iteration: 8, Log-Lik: -1601.339, Max-Change: 0.05903
Iteration: 9, Log-Lik: -1601.290, Max-Change: 0.05404
Iteration: 10, Log-Lik: -1601.157, Max-Change: 0.02478
Iteration: 11, Log-Lik: -1601.150, Max-Change: 0.01802
Iteration: 12, Log-Lik: -1601.147, Max-Change: 0.01519
Iteration: 13, Log-Lik: -1601.140, Max-Change: 0.00700
Iteration: 14, Log-Lik: -1601.140, Max-Change: 0.00638
Iteration: 15, Log-Lik: -1601.139, Max-Change: 0.00643
Iteration: 16, Log-Lik: -1601.138, Max-Change: 0.00185
Iteration: 17, Log-Lik: -1601.138, Max-Change: 0.00057
Iteration: 18, Log-Lik: -1601.138, Max-Change: 0.00051
Iteration: 19, Log-Lik: -1601.138, Max-Change: 0.00042
Iteration: 20, Log-Lik: -1601.138, Max-Change: 0.00044
Iteration: 21, Log-Lik: -1601.138, Max-Change: 0.00046
Iteration: 22, Log-Lik: -1601.138, Max-Change: 0.00046
Iteration: 23, Log-Lik: -1601.138, Max-Change: 0.00047
Iteration: 24, Log-Lik: -1601.138, Max-Change: 0.00055
Iteration: 25, Log-Lik: -1601.138, Max-Change: 0.00047
Iteration: 26, Log-Lik: -1601.138, Max-Change: 0.00047
Iteration: 27, Log-Lik: -1601.138, Max-Change: 0.00054
Iteration: 28, Log-Lik: -1601.138, Max-Change: 0.00046
Iteration: 29, Log-Lik: -1601.138, Max-Change: 0.00046
Iteration: 30, Log-Lik: -1601.138, Max-Change: 0.00050
Iteration: 31, Log-Lik: -1601.138, Max-Change: 0.00045
Iteration: 32, Log-Lik: -1601.138, Max-Change: 0.00045
Iteration: 33, Log-Lik: -1601.138, Max-Change: 0.00050
Iteration: 34, Log-Lik: -1601.138, Max-Change: 0.00044
Iteration: 35, Log-Lik: -1601.138, Max-Change: 0.00044
Iteration: 36, Log-Lik: -1601.138, Max-Change: 0.00047
Iteration: 37, Log-Lik: -1601.138, Max-Change: 0.00043
Iteration: 38, Log-Lik: -1601.138, Max-Change: 0.00043
Iteration: 39, Log-Lik: -1601.138, Max-Change: 0.00047
Iteration: 40, Log-Lik: -1601.138, Max-Change: 0.00042
Iteration: 41, Log-Lik: -1601.138, Max-Change: 0.00042
Iteration: 42, Log-Lik: -1601.138, Max-Change: 0.00044
Iteration: 43, Log-Lik: -1601.138, Max-Change: 0.00041
Iteration: 44, Log-Lik: -1601.138, Max-Change: 0.00040
Iteration: 45, Log-Lik: -1601.138, Max-Change: 0.00043
Iteration: 46, Log-Lik: -1601.138, Max-Change: 0.00040
Iteration: 47, Log-Lik: -1601.138, Max-Change: 0.00039
Iteration: 48, Log-Lik: -1601.138, Max-Change: 0.00041
Iteration: 49, Log-Lik: -1601.138, Max-Change: 0.00039
Iteration: 50, Log-Lik: -1601.138, Max-Change: 0.00038
Iteration: 51, Log-Lik: -1601.138, Max-Change: 0.00041
Iteration: 52, Log-Lik: -1601.138, Max-Change: 0.00038
Iteration: 53, Log-Lik: -1601.138, Max-Change: 0.00037
Iteration: 54, Log-Lik: -1601.138, Max-Change: 0.00039
Iteration: 55, Log-Lik: -1601.138, Max-Change: 0.00037
Iteration: 56, Log-Lik: -1601.137, Max-Change: 0.00036
Iteration: 57, Log-Lik: -1601.137, Max-Change: 0.00038
Iteration: 58, Log-Lik: -1601.137, Max-Change: 0.00036
Iteration: 59, Log-Lik: -1601.137, Max-Change: 0.00035
Iteration: 60, Log-Lik: -1601.137, Max-Change: 0.00037
Iteration: 61, Log-Lik: -1601.137, Max-Change: 0.00035
Iteration: 62, Log-Lik: -1601.137, Max-Change: 0.00034
Iteration: 63, Log-Lik: -1601.137, Max-Change: 0.00036
Iteration: 64, Log-Lik: -1601.137, Max-Change: 0.00034
Iteration: 65, Log-Lik: -1601.137, Max-Change: 0.00033
Iteration: 66, Log-Lik: -1601.137, Max-Change: 0.00035
Iteration: 67, Log-Lik: -1601.137, Max-Change: 0.00033
Iteration: 68, Log-Lik: -1601.137, Max-Change: 0.00032
Iteration: 69, Log-Lik: -1601.137, Max-Change: 0.00034
Iteration: 70, Log-Lik: -1601.137, Max-Change: 0.00032
Iteration: 71, Log-Lik: -1601.137, Max-Change: 0.00031
Iteration: 72, Log-Lik: -1601.137, Max-Change: 0.00033
Iteration: 73, Log-Lik: -1601.137, Max-Change: 0.00031
Iteration: 74, Log-Lik: -1601.137, Max-Change: 0.00031
Iteration: 75, Log-Lik: -1601.137, Max-Change: 0.00032
Iteration: 76, Log-Lik: -1601.137, Max-Change: 0.00030
Iteration: 77, Log-Lik: -1601.137, Max-Change: 0.00030
Iteration: 78, Log-Lik: -1601.137, Max-Change: 0.00031
Iteration: 79, Log-Lik: -1601.137, Max-Change: 0.00029
Iteration: 80, Log-Lik: -1601.137, Max-Change: 0.00029
Iteration: 81, Log-Lik: -1601.137, Max-Change: 0.00030
Iteration: 82, Log-Lik: -1601.137, Max-Change: 0.00028
Iteration: 83, Log-Lik: -1601.137, Max-Change: 0.00028
Iteration: 84, Log-Lik: -1601.137, Max-Change: 0.00029
Iteration: 85, Log-Lik: -1601.137, Max-Change: 0.00028
Iteration: 86, Log-Lik: -1601.137, Max-Change: 0.00027
Iteration: 87, Log-Lik: -1601.137, Max-Change: 0.00029
Iteration: 88, Log-Lik: -1601.137, Max-Change: 0.00027
Iteration: 89, Log-Lik: -1601.137, Max-Change: 0.00027
Iteration: 90, Log-Lik: -1601.137, Max-Change: 0.00028
Iteration: 91, Log-Lik: -1601.137, Max-Change: 0.00026
Iteration: 92, Log-Lik: -1601.137, Max-Change: 0.00026
Iteration: 93, Log-Lik: -1601.137, Max-Change: 0.00027
Iteration: 94, Log-Lik: -1601.137, Max-Change: 0.00025
Iteration: 95, Log-Lik: -1601.137, Max-Change: 0.00025
Iteration: 96, Log-Lik: -1601.137, Max-Change: 0.00026
Iteration: 97, Log-Lik: -1601.137, Max-Change: 0.00025
Iteration: 98, Log-Lik: -1601.137, Max-Change: 0.00024
Iteration: 99, Log-Lik: -1601.137, Max-Change: 0.00025
Iteration: 100, Log-Lik: -1601.137, Max-Change: 0.00024
Iteration: 101, Log-Lik: -1601.137, Max-Change: 0.00024
Iteration: 102, Log-Lik: -1601.137, Max-Change: 0.00025
Iteration: 103, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 104, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 105, Log-Lik: -1601.137, Max-Change: 0.00024
Iteration: 106, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 107, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 108, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 109, Log-Lik: -1601.137, Max-Change: 0.00022
Iteration: 110, Log-Lik: -1601.137, Max-Change: 0.00022
Iteration: 111, Log-Lik: -1601.137, Max-Change: 0.00023
Iteration: 112, Log-Lik: -1601.137, Max-Change: 0.00022
Iteration: 113, Log-Lik: -1601.137, Max-Change: 0.00021
Iteration: 114, Log-Lik: -1601.137, Max-Change: 0.00022
Iteration: 115, Log-Lik: -1601.137, Max-Change: 0.00021
Iteration: 116, Log-Lik: -1601.137, Max-Change: 0.00021
Iteration: 117, Log-Lik: -1601.137, Max-Change: 0.00022
Iteration: 118, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 119, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 120, Log-Lik: -1601.137, Max-Change: 0.00021
Iteration: 121, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 122, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 123, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 124, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 125, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 126, Log-Lik: -1601.137, Max-Change: 0.00020
Iteration: 127, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 128, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 129, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 130, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 131, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 132, Log-Lik: -1601.137, Max-Change: 0.00019
Iteration: 133, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 134, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 135, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 136, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 137, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 138, Log-Lik: -1601.137, Max-Change: 0.00018
Iteration: 139, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 140, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 141, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 142, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 143, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 144, Log-Lik: -1601.137, Max-Change: 0.00017
Iteration: 145, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 146, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 147, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 148, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 149, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 150, Log-Lik: -1601.137, Max-Change: 0.00016
Iteration: 151, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 152, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 153, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 154, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 155, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 156, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 157, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 158, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 159, Log-Lik: -1601.137, Max-Change: 0.00015
Iteration: 160, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 161, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 162, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 163, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 164, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 165, Log-Lik: -1601.137, Max-Change: 0.00014
Iteration: 166, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 167, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 168, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 169, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 170, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 171, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 172, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 173, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 174, Log-Lik: -1601.137, Max-Change: 0.00013
Iteration: 175, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 176, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 177, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 178, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 179, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 180, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 181, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 182, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 183, Log-Lik: -1601.137, Max-Change: 0.00012
Iteration: 184, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 185, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 186, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 187, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 188, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 189, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 190, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 191, Log-Lik: -1601.137, Max-Change: 0.00010
Iteration: 192, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 193, Log-Lik: -1601.137, Max-Change: 0.00010
Iteration: 194, Log-Lik: -1601.137, Max-Change: 0.00010
Iteration: 195, Log-Lik: -1601.137, Max-Change: 0.00011
Iteration: 196, Log-Lik: -1601.137, Max-Change: 0.00010
Iteration: 197, Log-Lik: -1601.137, Max-Change: 0.00010
plot(x2)

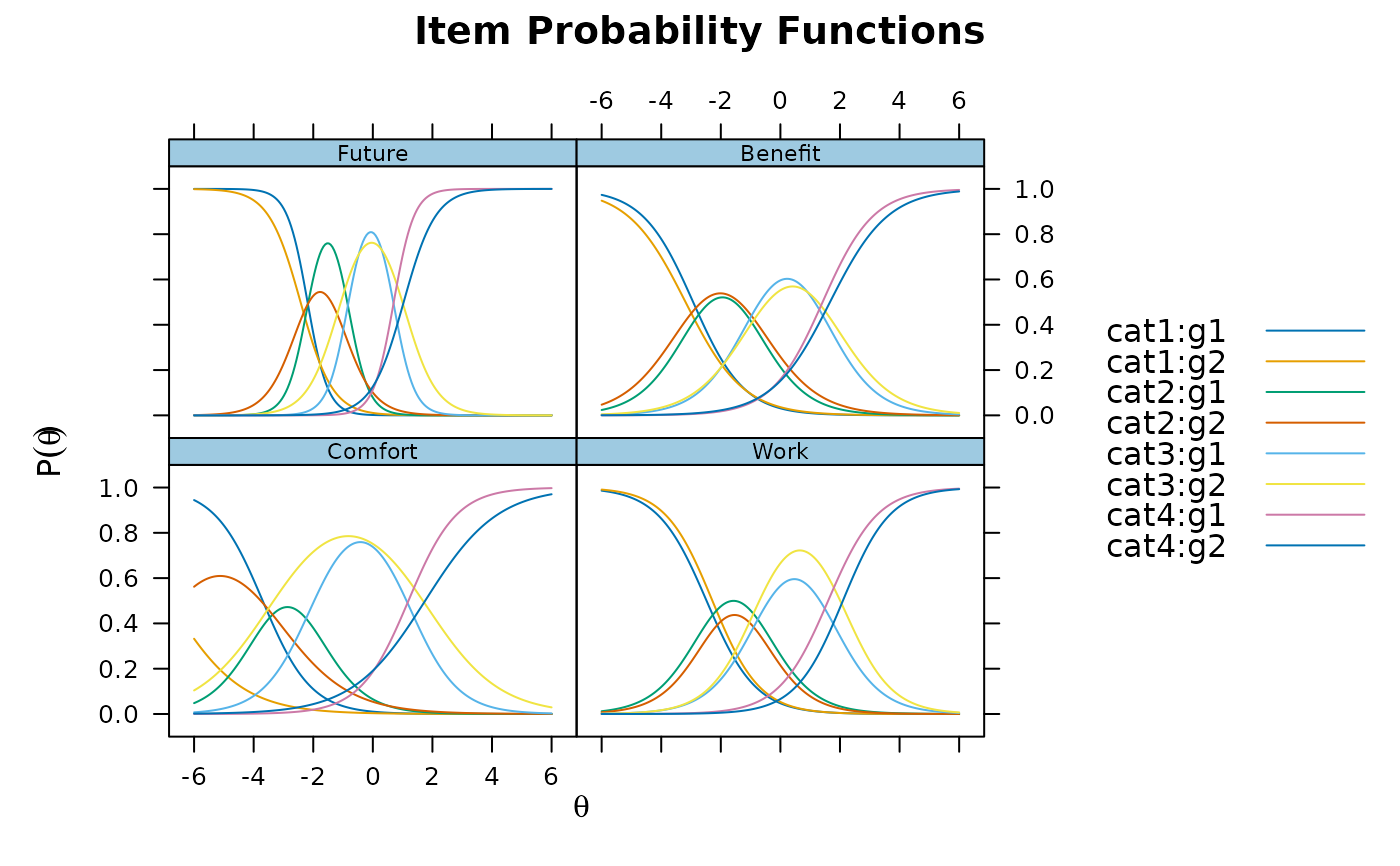plot(x2, type = 'trace')

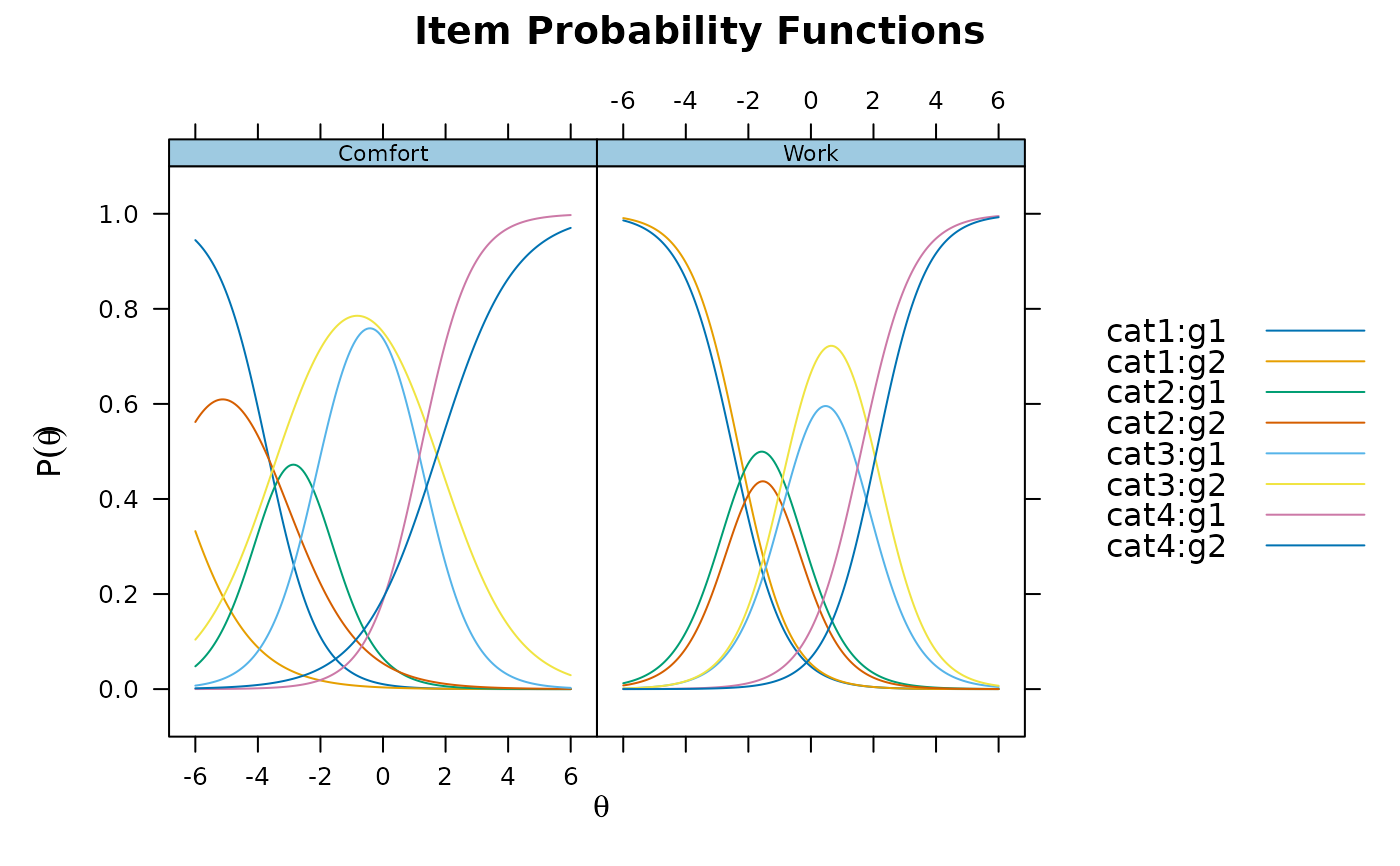plot(x2, type = 'trace', which.items = 1:2)

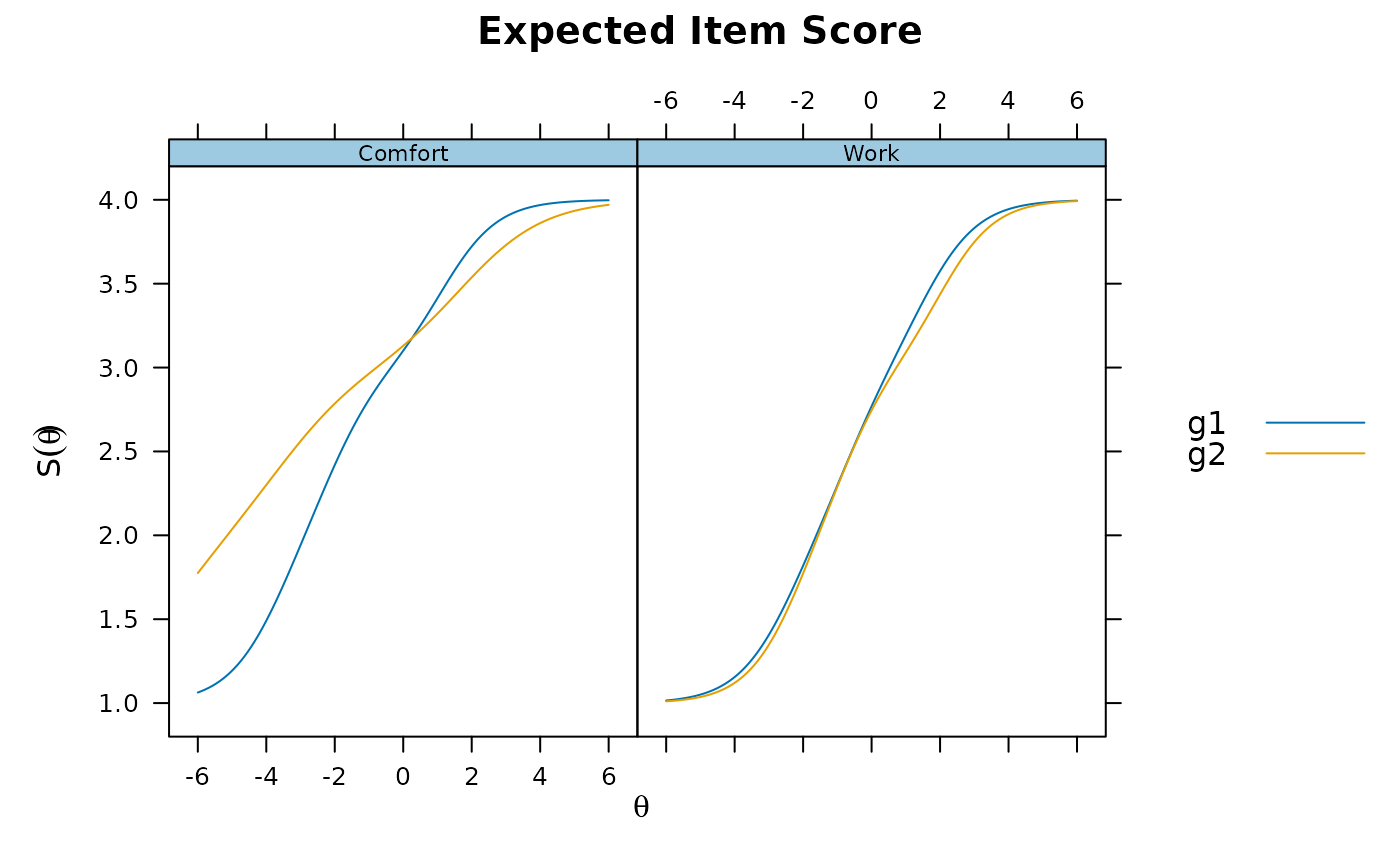plot(x2, type = 'itemscore', which.items = 1:2)

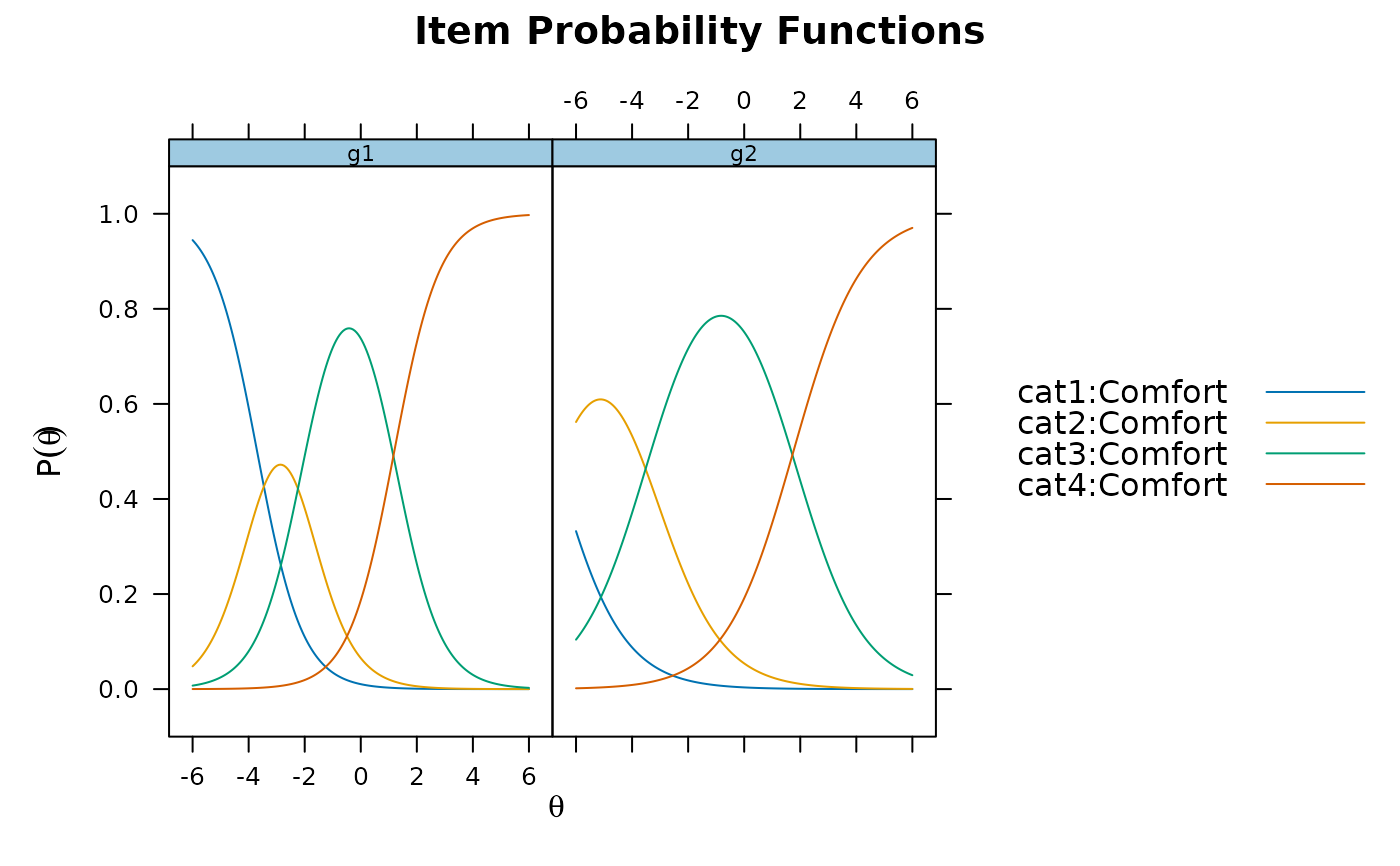plot(x2, type = 'trace', which.items = 1, facet_items = FALSE) #facet by group

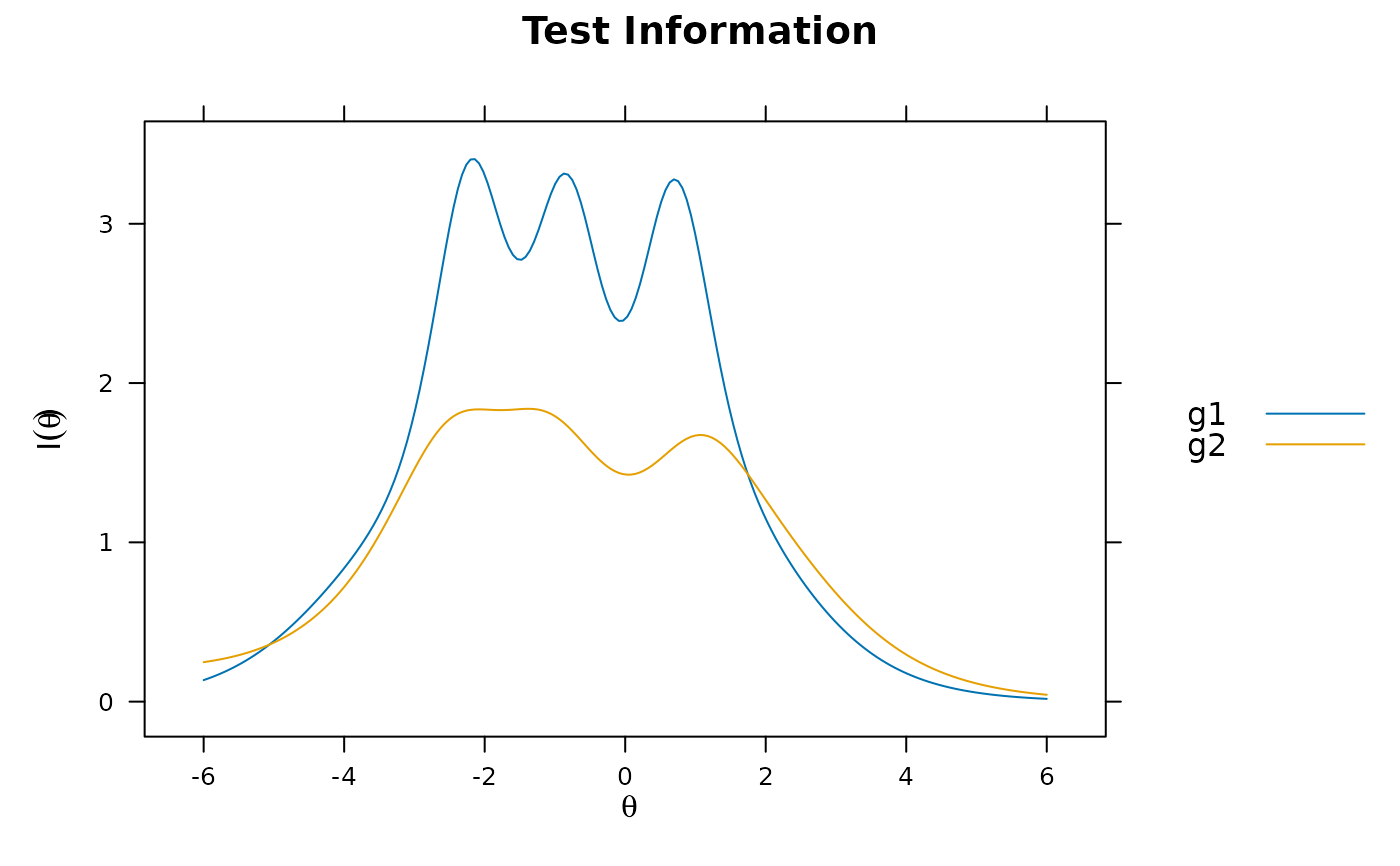plot(x2, type = 'info')


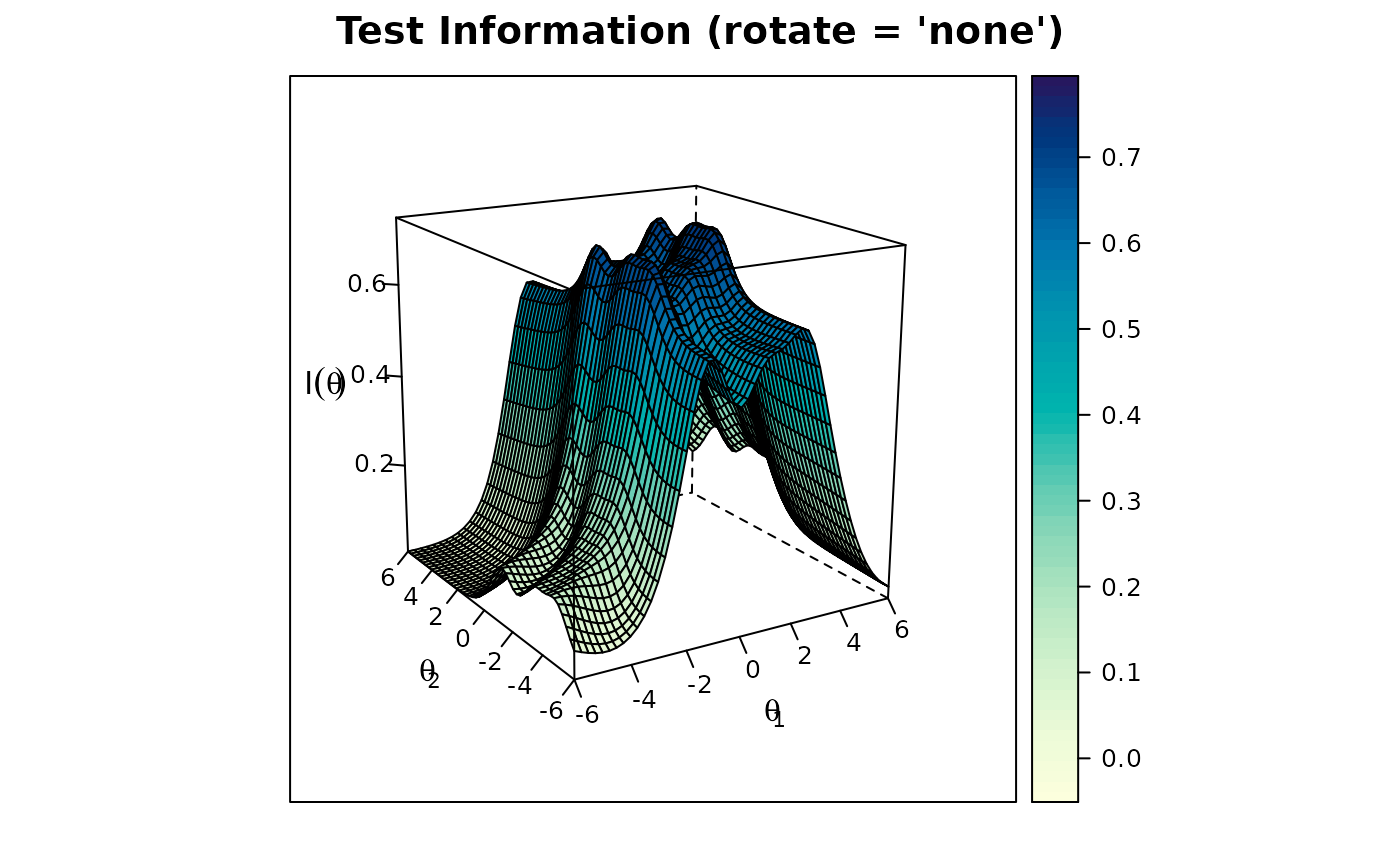
x3 <- mirt(Science, 2)
#> 
Iteration: 1, Log-Lik: -1634.562, Max-Change: 0.49365
Iteration: 2, Log-Lik: -1608.496, Max-Change: 0.17069
Iteration: 3, Log-Lik: -1604.784, Max-Change: 0.08523
Iteration: 4, Log-Lik: -1604.195, Max-Change: 0.05345
Iteration: 5, Log-Lik: -1603.777, Max-Change: 0.03491
Iteration: 6, Log-Lik: -1603.581, Max-Change: 0.02948
Iteration: 7, Log-Lik: -1603.263, Max-Change: 0.02614
Iteration: 8, Log-Lik: -1603.177, Max-Change: 0.02281
Iteration: 9, Log-Lik: -1603.099, Max-Change: 0.02311
Iteration: 10, Log-Lik: -1602.717, Max-Change: 0.01961
Iteration: 11, Log-Lik: -1602.673, Max-Change: 0.01556
Iteration: 12, Log-Lik: -1602.635, Max-Change: 0.01694
Iteration: 13, Log-Lik: -1602.443, Max-Change: 0.01534
Iteration: 14, Log-Lik: -1602.421, Max-Change: 0.01311
Iteration: 15, Log-Lik: -1602.401, Max-Change: 0.01384
Iteration: 16, Log-Lik: -1602.303, Max-Change: 0.00987
Iteration: 17, Log-Lik: -1602.288, Max-Change: 0.01006
Iteration: 18, Log-Lik: -1602.275, Max-Change: 0.00939
Iteration: 19, Log-Lik: -1602.206, Max-Change: 0.00972
Iteration: 20, Log-Lik: -1602.198, Max-Change: 0.01016
Iteration: 21, Log-Lik: -1602.189, Max-Change: 0.00670
Iteration: 22, Log-Lik: -1602.165, Max-Change: 0.00679
Iteration: 23, Log-Lik: -1602.158, Max-Change: 0.00694
Iteration: 24, Log-Lik: -1602.152, Max-Change: 0.00555
Iteration: 25, Log-Lik: -1602.116, Max-Change: 0.00689
Iteration: 26, Log-Lik: -1602.112, Max-Change: 0.00465
Iteration: 27, Log-Lik: -1602.107, Max-Change: 0.00478
Iteration: 28, Log-Lik: -1602.082, Max-Change: 0.00389
Iteration: 29, Log-Lik: -1602.078, Max-Change: 0.00745
Iteration: 30, Log-Lik: -1602.074, Max-Change: 0.00380
Iteration: 31, Log-Lik: -1602.069, Max-Change: 0.00373
Iteration: 32, Log-Lik: -1602.066, Max-Change: 0.00792
Iteration: 33, Log-Lik: -1602.063, Max-Change: 0.00397
Iteration: 34, Log-Lik: -1602.060, Max-Change: 0.00364
Iteration: 35, Log-Lik: -1602.057, Max-Change: 0.00808
Iteration: 36, Log-Lik: -1602.055, Max-Change: 0.00332
Iteration: 37, Log-Lik: -1602.052, Max-Change: 0.00613
Iteration: 38, Log-Lik: -1602.049, Max-Change: 0.00319
Iteration: 39, Log-Lik: -1602.047, Max-Change: 0.00596
Iteration: 40, Log-Lik: -1602.043, Max-Change: 0.00303
Iteration: 41, Log-Lik: -1602.040, Max-Change: 0.00302
Iteration: 42, Log-Lik: -1602.038, Max-Change: 0.00611
Iteration: 43, Log-Lik: -1602.034, Max-Change: 0.00392
Iteration: 44, Log-Lik: -1602.033, Max-Change: 0.00329
Iteration: 45, Log-Lik: -1602.030, Max-Change: 0.00406
Iteration: 46, Log-Lik: -1602.026, Max-Change: 0.00303
Iteration: 47, Log-Lik: -1602.025, Max-Change: 0.00261
Iteration: 48, Log-Lik: -1602.023, Max-Change: 0.00457
Iteration: 49, Log-Lik: -1602.021, Max-Change: 0.00265
Iteration: 50, Log-Lik: -1602.020, Max-Change: 0.00290
Iteration: 51, Log-Lik: -1602.018, Max-Change: 0.00268
Iteration: 52, Log-Lik: -1602.010, Max-Change: 0.00310
Iteration: 53, Log-Lik: -1602.008, Max-Change: 0.00361
Iteration: 54, Log-Lik: -1602.007, Max-Change: 0.00238
Iteration: 55, Log-Lik: -1602.006, Max-Change: 0.00327
Iteration: 56, Log-Lik: -1602.005, Max-Change: 0.00269
Iteration: 57, Log-Lik: -1602.004, Max-Change: 0.00324
Iteration: 58, Log-Lik: -1602.002, Max-Change: 0.00218
Iteration: 59, Log-Lik: -1602.001, Max-Change: 0.00198
Iteration: 60, Log-Lik: -1602.000, Max-Change: 0.00346
Iteration: 61, Log-Lik: -1601.999, Max-Change: 0.00226
Iteration: 62, Log-Lik: -1601.998, Max-Change: 0.00247
Iteration: 63, Log-Lik: -1601.997, Max-Change: 0.00264
Iteration: 64, Log-Lik: -1601.996, Max-Change: 0.00380
Iteration: 65, Log-Lik: -1601.995, Max-Change: 0.00236
Iteration: 66, Log-Lik: -1601.994, Max-Change: 0.00244
Iteration: 67, Log-Lik: -1601.992, Max-Change: 0.00164
Iteration: 68, Log-Lik: -1601.992, Max-Change: 0.00214
Iteration: 69, Log-Lik: -1601.991, Max-Change: 0.00193
Iteration: 70, Log-Lik: -1601.990, Max-Change: 0.00267
Iteration: 71, Log-Lik: -1601.989, Max-Change: 0.00227
Iteration: 72, Log-Lik: -1601.989, Max-Change: 0.00232
Iteration: 73, Log-Lik: -1601.988, Max-Change: 0.00172
Iteration: 74, Log-Lik: -1601.987, Max-Change: 0.00149
Iteration: 75, Log-Lik: -1601.987, Max-Change: 0.00245
Iteration: 76, Log-Lik: -1601.986, Max-Change: 0.00149
Iteration: 77, Log-Lik: -1601.985, Max-Change: 0.00215
Iteration: 78, Log-Lik: -1601.985, Max-Change: 0.00206
Iteration: 79, Log-Lik: -1601.984, Max-Change: 0.00223
Iteration: 80, Log-Lik: -1601.983, Max-Change: 0.00190
Iteration: 81, Log-Lik: -1601.983, Max-Change: 0.00181
Iteration: 82, Log-Lik: -1601.982, Max-Change: 0.00125
Iteration: 83, Log-Lik: -1601.981, Max-Change: 0.00136
Iteration: 84, Log-Lik: -1601.981, Max-Change: 0.00207
Iteration: 85, Log-Lik: -1601.981, Max-Change: 0.00124
Iteration: 86, Log-Lik: -1601.980, Max-Change: 0.00187
Iteration: 87, Log-Lik: -1601.980, Max-Change: 0.00123
Iteration: 88, Log-Lik: -1601.980, Max-Change: 0.00193
Iteration: 89, Log-Lik: -1601.980, Max-Change: 0.00123
Iteration: 90, Log-Lik: -1601.979, Max-Change: 0.00198
Iteration: 91, Log-Lik: -1601.979, Max-Change: 0.00118
Iteration: 92, Log-Lik: -1601.979, Max-Change: 0.00121
Iteration: 93, Log-Lik: -1601.979, Max-Change: 0.00196
Iteration: 94, Log-Lik: -1601.978, Max-Change: 0.00112
Iteration: 95, Log-Lik: -1601.978, Max-Change: 0.00117
Iteration: 96, Log-Lik: -1601.978, Max-Change: 0.00193
Iteration: 97, Log-Lik: -1601.978, Max-Change: 0.00106
Iteration: 98, Log-Lik: -1601.977, Max-Change: 0.00112
Iteration: 99, Log-Lik: -1601.977, Max-Change: 0.00187
Iteration: 100, Log-Lik: -1601.977, Max-Change: 0.00103
Iteration: 101, Log-Lik: -1601.977, Max-Change: 0.00109
Iteration: 102, Log-Lik: -1601.977, Max-Change: 0.00127
Iteration: 103, Log-Lik: -1601.976, Max-Change: 0.00118
Iteration: 104, Log-Lik: -1601.976, Max-Change: 0.00115
Iteration: 105, Log-Lik: -1601.976, Max-Change: 0.00115
Iteration: 106, Log-Lik: -1601.975, Max-Change: 0.00108
Iteration: 107, Log-Lik: -1601.975, Max-Change: 0.00108
Iteration: 108, Log-Lik: -1601.975, Max-Change: 0.00107
Iteration: 109, Log-Lik: -1601.974, Max-Change: 0.00103
Iteration: 110, Log-Lik: -1601.974, Max-Change: 0.00102
Iteration: 111, Log-Lik: -1601.974, Max-Change: 0.00101
Iteration: 112, Log-Lik: -1601.974, Max-Change: 0.00083
Iteration: 113, Log-Lik: -1601.974, Max-Change: 0.00088
Iteration: 114, Log-Lik: -1601.974, Max-Change: 0.00090
Iteration: 115, Log-Lik: -1601.973, Max-Change: 0.00108
Iteration: 116, Log-Lik: -1601.973, Max-Change: 0.00037
Iteration: 117, Log-Lik: -1601.973, Max-Change: 0.00138
Iteration: 118, Log-Lik: -1601.973, Max-Change: 0.00320
Iteration: 119, Log-Lik: -1601.973, Max-Change: 0.00085
Iteration: 120, Log-Lik: -1601.973, Max-Change: 0.00039
Iteration: 121, Log-Lik: -1601.973, Max-Change: 0.00034
Iteration: 122, Log-Lik: -1601.973, Max-Change: 0.00026
Iteration: 123, Log-Lik: -1601.973, Max-Change: 0.00109
Iteration: 124, Log-Lik: -1601.973, Max-Change: 0.00128
Iteration: 125, Log-Lik: -1601.973, Max-Change: 0.00113
Iteration: 126, Log-Lik: -1601.973, Max-Change: 0.00094
Iteration: 127, Log-Lik: -1601.973, Max-Change: 0.00080
Iteration: 128, Log-Lik: -1601.972, Max-Change: 0.00028
Iteration: 129, Log-Lik: -1601.972, Max-Change: 0.00105
Iteration: 130, Log-Lik: -1601.972, Max-Change: 0.00291
Iteration: 131, Log-Lik: -1601.972, Max-Change: 0.00082
Iteration: 132, Log-Lik: -1601.972, Max-Change: 0.00034
Iteration: 133, Log-Lik: -1601.972, Max-Change: 0.00029
Iteration: 134, Log-Lik: -1601.972, Max-Change: 0.00112
Iteration: 135, Log-Lik: -1601.972, Max-Change: 0.00244
Iteration: 136, Log-Lik: -1601.972, Max-Change: 0.00039
Iteration: 137, Log-Lik: -1601.972, Max-Change: 0.00027
Iteration: 138, Log-Lik: -1601.972, Max-Change: 0.00022
Iteration: 139, Log-Lik: -1601.972, Max-Change: 0.00112
Iteration: 140, Log-Lik: -1601.972, Max-Change: 0.00024
Iteration: 141, Log-Lik: -1601.972, Max-Change: 0.00098
Iteration: 142, Log-Lik: -1601.972, Max-Change: 0.00261
Iteration: 143, Log-Lik: -1601.972, Max-Change: 0.00031
Iteration: 144, Log-Lik: -1601.972, Max-Change: 0.00023
Iteration: 145, Log-Lik: -1601.972, Max-Change: 0.00208
Iteration: 146, Log-Lik: -1601.972, Max-Change: 0.00074
Iteration: 147, Log-Lik: -1601.972, Max-Change: 0.00031
Iteration: 148, Log-Lik: -1601.972, Max-Change: 0.00027
Iteration: 149, Log-Lik: -1601.971, Max-Change: 0.00104
Iteration: 150, Log-Lik: -1601.971, Max-Change: 0.00114
Iteration: 151, Log-Lik: -1601.971, Max-Change: 0.00026
Iteration: 152, Log-Lik: -1601.971, Max-Change: 0.00099
Iteration: 153, Log-Lik: -1601.971, Max-Change: 0.00235
Iteration: 154, Log-Lik: -1601.971, Max-Change: 0.00028
Iteration: 155, Log-Lik: -1601.971, Max-Change: 0.00022
Iteration: 156, Log-Lik: -1601.971, Max-Change: 0.00019
Iteration: 157, Log-Lik: -1601.971, Max-Change: 0.00104
Iteration: 158, Log-Lik: -1601.971, Max-Change: 0.00023
Iteration: 159, Log-Lik: -1601.971, Max-Change: 0.00088
Iteration: 160, Log-Lik: -1601.971, Max-Change: 0.00085
Iteration: 161, Log-Lik: -1601.971, Max-Change: 0.00030
Iteration: 162, Log-Lik: -1601.971, Max-Change: 0.00019
Iteration: 163, Log-Lik: -1601.971, Max-Change: 0.00075
Iteration: 164, Log-Lik: -1601.971, Max-Change: 0.00106
Iteration: 165, Log-Lik: -1601.971, Max-Change: 0.00093
Iteration: 166, Log-Lik: -1601.971, Max-Change: 0.00081
Iteration: 167, Log-Lik: -1601.971, Max-Change: 0.00068
Iteration: 168, Log-Lik: -1601.971, Max-Change: 0.00022
Iteration: 169, Log-Lik: -1601.971, Max-Change: 0.00020
Iteration: 170, Log-Lik: -1601.971, Max-Change: 0.00080
Iteration: 171, Log-Lik: -1601.971, Max-Change: 0.00104
Iteration: 172, Log-Lik: -1601.971, Max-Change: 0.00026
Iteration: 173, Log-Lik: -1601.971, Max-Change: 0.00019
Iteration: 174, Log-Lik: -1601.971, Max-Change: 0.00078
Iteration: 175, Log-Lik: -1601.971, Max-Change: 0.00103
Iteration: 176, Log-Lik: -1601.971, Max-Change: 0.00071
Iteration: 177, Log-Lik: -1601.971, Max-Change: 0.00014
Iteration: 178, Log-Lik: -1601.971, Max-Change: 0.00066
Iteration: 179, Log-Lik: -1601.971, Max-Change: 0.00021
Iteration: 180, Log-Lik: -1601.971, Max-Change: 0.00065
Iteration: 181, Log-Lik: -1601.971, Max-Change: 0.00147
Iteration: 182, Log-Lik: -1601.970, Max-Change: 0.00020
Iteration: 183, Log-Lik: -1601.970, Max-Change: 0.00017
Iteration: 184, Log-Lik: -1601.970, Max-Change: 0.00062
Iteration: 185, Log-Lik: -1601.970, Max-Change: 0.00058
Iteration: 186, Log-Lik: -1601.970, Max-Change: 0.00064
Iteration: 187, Log-Lik: -1601.970, Max-Change: 0.00105
Iteration: 188, Log-Lik: -1601.970, Max-Change: 0.00019
Iteration: 189, Log-Lik: -1601.970, Max-Change: 0.00077
Iteration: 190, Log-Lik: -1601.970, Max-Change: 0.00071
Iteration: 191, Log-Lik: -1601.970, Max-Change: 0.00021
Iteration: 192, Log-Lik: -1601.970, Max-Change: 0.00077
Iteration: 193, Log-Lik: -1601.970, Max-Change: 0.00081
Iteration: 194, Log-Lik: -1601.970, Max-Change: 0.00028
Iteration: 195, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 196, Log-Lik: -1601.970, Max-Change: 0.00069
Iteration: 197, Log-Lik: -1601.970, Max-Change: 0.00063
Iteration: 198, Log-Lik: -1601.970, Max-Change: 0.00020
Iteration: 199, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 200, Log-Lik: -1601.970, Max-Change: 0.00068
Iteration: 201, Log-Lik: -1601.970, Max-Change: 0.00064
Iteration: 202, Log-Lik: -1601.970, Max-Change: 0.00023
Iteration: 203, Log-Lik: -1601.970, Max-Change: 0.00016
Iteration: 204, Log-Lik: -1601.970, Max-Change: 0.00062
Iteration: 205, Log-Lik: -1601.970, Max-Change: 0.00064
Iteration: 206, Log-Lik: -1601.970, Max-Change: 0.00021
Iteration: 207, Log-Lik: -1601.970, Max-Change: 0.00072
Iteration: 208, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 209, Log-Lik: -1601.970, Max-Change: 0.00061
Iteration: 210, Log-Lik: -1601.970, Max-Change: 0.00020
Iteration: 211, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 212, Log-Lik: -1601.970, Max-Change: 0.00067
Iteration: 213, Log-Lik: -1601.970, Max-Change: 0.00065
Iteration: 214, Log-Lik: -1601.970, Max-Change: 0.00021
Iteration: 215, Log-Lik: -1601.970, Max-Change: 0.00014
Iteration: 216, Log-Lik: -1601.970, Max-Change: 0.00058
Iteration: 217, Log-Lik: -1601.970, Max-Change: 0.00060
Iteration: 218, Log-Lik: -1601.970, Max-Change: 0.00020
Iteration: 219, Log-Lik: -1601.970, Max-Change: 0.00068
Iteration: 220, Log-Lik: -1601.970, Max-Change: 0.00019
Iteration: 221, Log-Lik: -1601.970, Max-Change: 0.00059
Iteration: 222, Log-Lik: -1601.970, Max-Change: 0.00019
Iteration: 223, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 224, Log-Lik: -1601.970, Max-Change: 0.00064
Iteration: 225, Log-Lik: -1601.970, Max-Change: 0.00013
Iteration: 226, Log-Lik: -1601.970, Max-Change: 0.00059
Iteration: 227, Log-Lik: -1601.970, Max-Change: 0.00020
Iteration: 228, Log-Lik: -1601.970, Max-Change: 0.00013
Iteration: 229, Log-Lik: -1601.970, Max-Change: 0.00054
Iteration: 230, Log-Lik: -1601.970, Max-Change: 0.00052
Iteration: 231, Log-Lik: -1601.970, Max-Change: 0.00015
Iteration: 232, Log-Lik: -1601.970, Max-Change: 0.00014
Iteration: 233, Log-Lik: -1601.970, Max-Change: 0.00055
Iteration: 234, Log-Lik: -1601.970, Max-Change: 0.00052
Iteration: 235, Log-Lik: -1601.970, Max-Change: 0.00019
Iteration: 236, Log-Lik: -1601.970, Max-Change: 0.00013
Iteration: 237, Log-Lik: -1601.970, Max-Change: 0.00053
Iteration: 238, Log-Lik: -1601.970, Max-Change: 0.00054
Iteration: 239, Log-Lik: -1601.970, Max-Change: 0.00017
Iteration: 240, Log-Lik: -1601.970, Max-Change: 0.00062
Iteration: 241, Log-Lik: -1601.970, Max-Change: 0.00017
Iteration: 242, Log-Lik: -1601.970, Max-Change: 0.00053
Iteration: 243, Log-Lik: -1601.970, Max-Change: 0.00017
Iteration: 244, Log-Lik: -1601.970, Max-Change: 0.00016
Iteration: 245, Log-Lik: -1601.970, Max-Change: 0.00058
Iteration: 246, Log-Lik: -1601.970, Max-Change: 0.00011
Iteration: 247, Log-Lik: -1601.970, Max-Change: 0.00054
Iteration: 248, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 249, Log-Lik: -1601.970, Max-Change: 0.00062
Iteration: 250, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 251, Log-Lik: -1601.970, Max-Change: 0.00054
Iteration: 252, Log-Lik: -1601.970, Max-Change: 0.00017
Iteration: 253, Log-Lik: -1601.970, Max-Change: 0.00016
Iteration: 254, Log-Lik: -1601.970, Max-Change: 0.00058
Iteration: 255, Log-Lik: -1601.970, Max-Change: 0.00012
Iteration: 256, Log-Lik: -1601.970, Max-Change: 0.00055
Iteration: 257, Log-Lik: -1601.970, Max-Change: 0.00018
Iteration: 258, Log-Lik: -1601.970, Max-Change: 0.00012
Iteration: 259, Log-Lik: -1601.970, Max-Change: 0.00050
Iteration: 260, Log-Lik: -1601.969, Max-Change: 0.00048
Iteration: 261, Log-Lik: -1601.969, Max-Change: 0.00014
Iteration: 262, Log-Lik: -1601.969, Max-Change: 0.00013
Iteration: 263, Log-Lik: -1601.969, Max-Change: 0.00051
Iteration: 264, Log-Lik: -1601.969, Max-Change: 0.00049
Iteration: 265, Log-Lik: -1601.969, Max-Change: 0.00017
Iteration: 266, Log-Lik: -1601.969, Max-Change: 0.00059
Iteration: 267, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 268, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 269, Log-Lik: -1601.969, Max-Change: 0.00047
Iteration: 270, Log-Lik: -1601.969, Max-Change: 0.00013
Iteration: 271, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 272, Log-Lik: -1601.969, Max-Change: 0.00049
Iteration: 273, Log-Lik: -1601.969, Max-Change: 0.00047
Iteration: 274, Log-Lik: -1601.969, Max-Change: 0.00016
Iteration: 275, Log-Lik: -1601.969, Max-Change: 0.00058
Iteration: 276, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 277, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 278, Log-Lik: -1601.969, Max-Change: 0.00046
Iteration: 279, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 280, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 281, Log-Lik: -1601.969, Max-Change: 0.00048
Iteration: 282, Log-Lik: -1601.969, Max-Change: 0.00047
Iteration: 283, Log-Lik: -1601.969, Max-Change: 0.00016
Iteration: 284, Log-Lik: -1601.969, Max-Change: 0.00056
Iteration: 285, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 286, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 287, Log-Lik: -1601.969, Max-Change: 0.00045
Iteration: 288, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 289, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 290, Log-Lik: -1601.969, Max-Change: 0.00047
Iteration: 291, Log-Lik: -1601.969, Max-Change: 0.00046
Iteration: 292, Log-Lik: -1601.969, Max-Change: 0.00016
Iteration: 293, Log-Lik: -1601.969, Max-Change: 0.00055
Iteration: 294, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 295, Log-Lik: -1601.969, Max-Change: 0.00010
Iteration: 296, Log-Lik: -1601.969, Max-Change: 0.00044
Iteration: 297, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 298, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 299, Log-Lik: -1601.969, Max-Change: 0.00046
Iteration: 300, Log-Lik: -1601.969, Max-Change: 0.00045
Iteration: 301, Log-Lik: -1601.969, Max-Change: 0.00015
Iteration: 302, Log-Lik: -1601.969, Max-Change: 0.00054
Iteration: 303, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 304, Log-Lik: -1601.969, Max-Change: 0.00010
Iteration: 305, Log-Lik: -1601.969, Max-Change: 0.00043
Iteration: 306, Log-Lik: -1601.969, Max-Change: 0.00012
Iteration: 307, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 308, Log-Lik: -1601.969, Max-Change: 0.00045
Iteration: 309, Log-Lik: -1601.969, Max-Change: 0.00044
Iteration: 310, Log-Lik: -1601.969, Max-Change: 0.00015
Iteration: 311, Log-Lik: -1601.969, Max-Change: 0.00053
Iteration: 312, Log-Lik: -1601.969, Max-Change: 0.00011
Iteration: 313, Log-Lik: -1601.969, Max-Change: 0.00010
plot(x3, type = 'info')

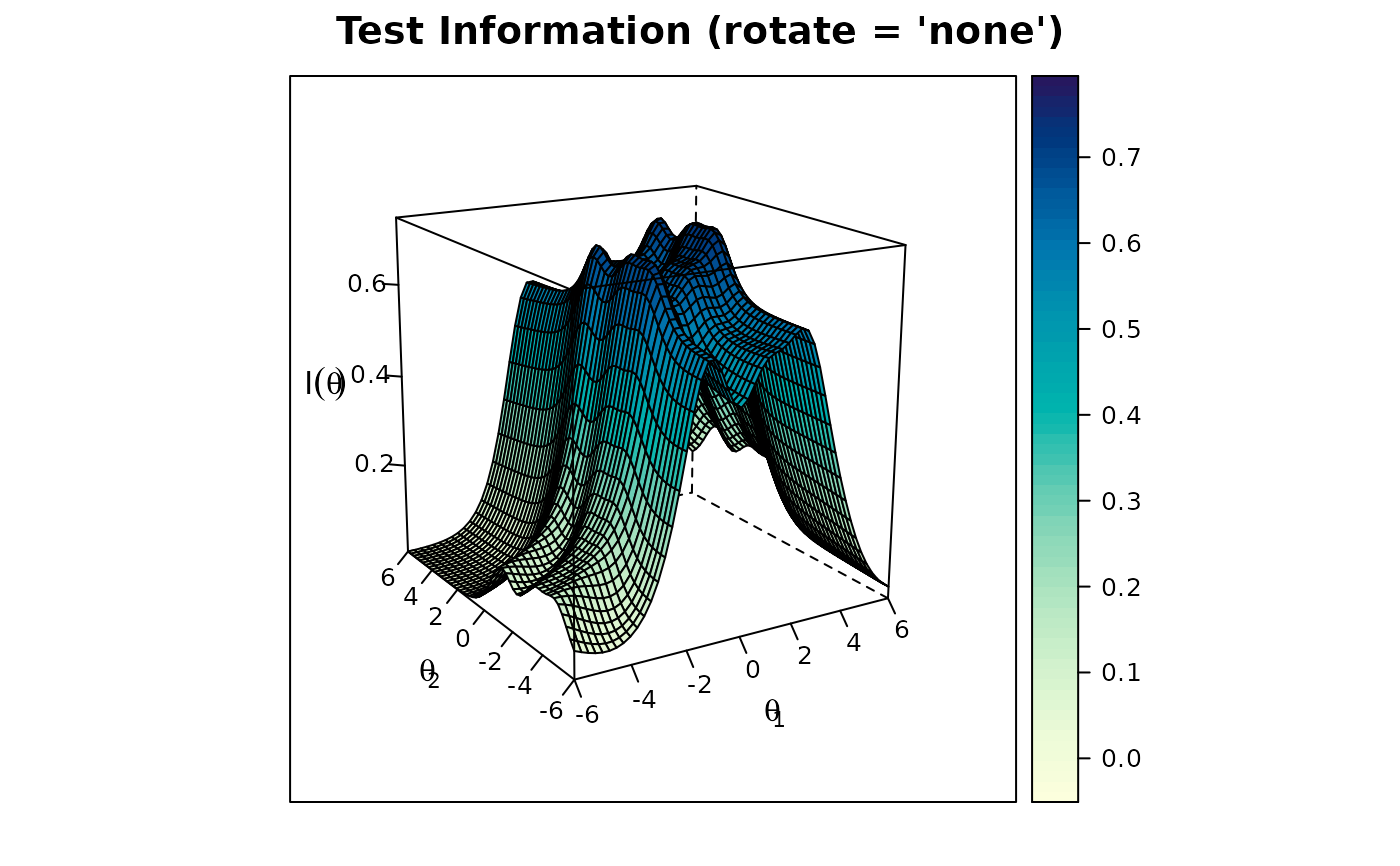plot(x3, type = 'SE', theta_lim = c(-3,3))


# }