Generate data with the multivariate g-and-h distribution

Source: R/rgenerate.R

Generate non-normal distributions using the multivariate g-and-h distribution. Can be used to generate several different classes of univariate and multivariate distributions.

rmgh(n, g, h, mean = rep(0, length(g)), sigma = diag(length(mean)))

Arguments

n

number of samples to draw

g

the g parameter(s) which control the skew of a distribution in terms of both direction and magnitude

h

the h parameter(s) which control the tail weight or elongation of a distribution and is positively related with kurtosis

mean

a vector of k elements for the mean of the variables

sigma

desired k x k covariance matrix between bivariate non-normal variables

References

Chalmers, R. P., & Adkins, M. C. (2020). Writing Effective and Reliable Monte Carlo Simulations with the SimDesign Package. The Quantitative Methods for Psychology, 16(4), 248-280. doi:10.20982/tqmp.16.4.p248

Sigal, M. J., & Chalmers, R. P. (2016). Play it again: Teaching statistics with Monte Carlo simulation. Journal of Statistics Education, 24(3), 136-156. doi:10.1080/10691898.2016.1246953

Author

Phil Chalmers rphilip.chalmers@gmail.com

Examples


set.seed(1)

# univariate
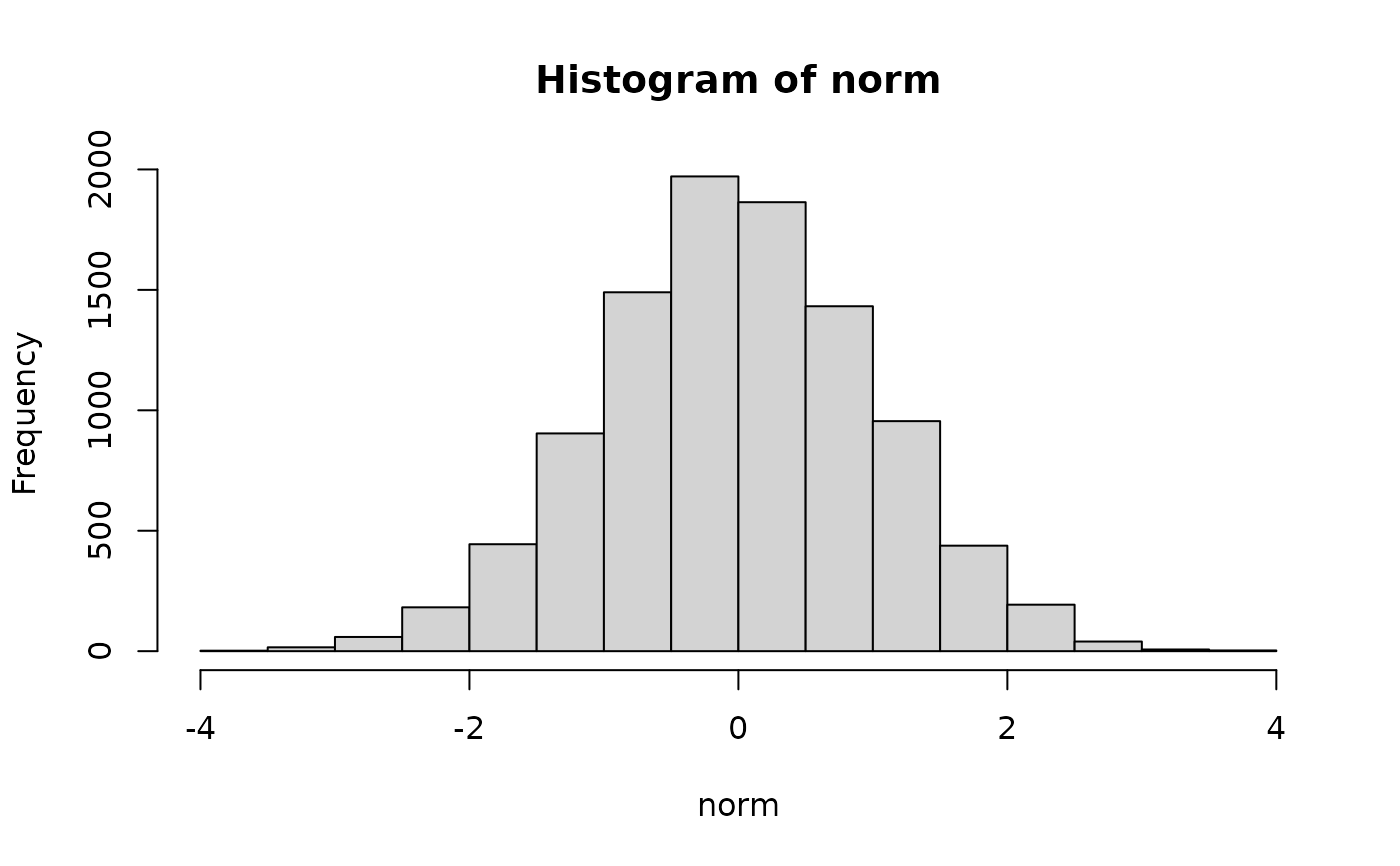
norm <- rmgh(10000,1e-5,0)
hist(norm)


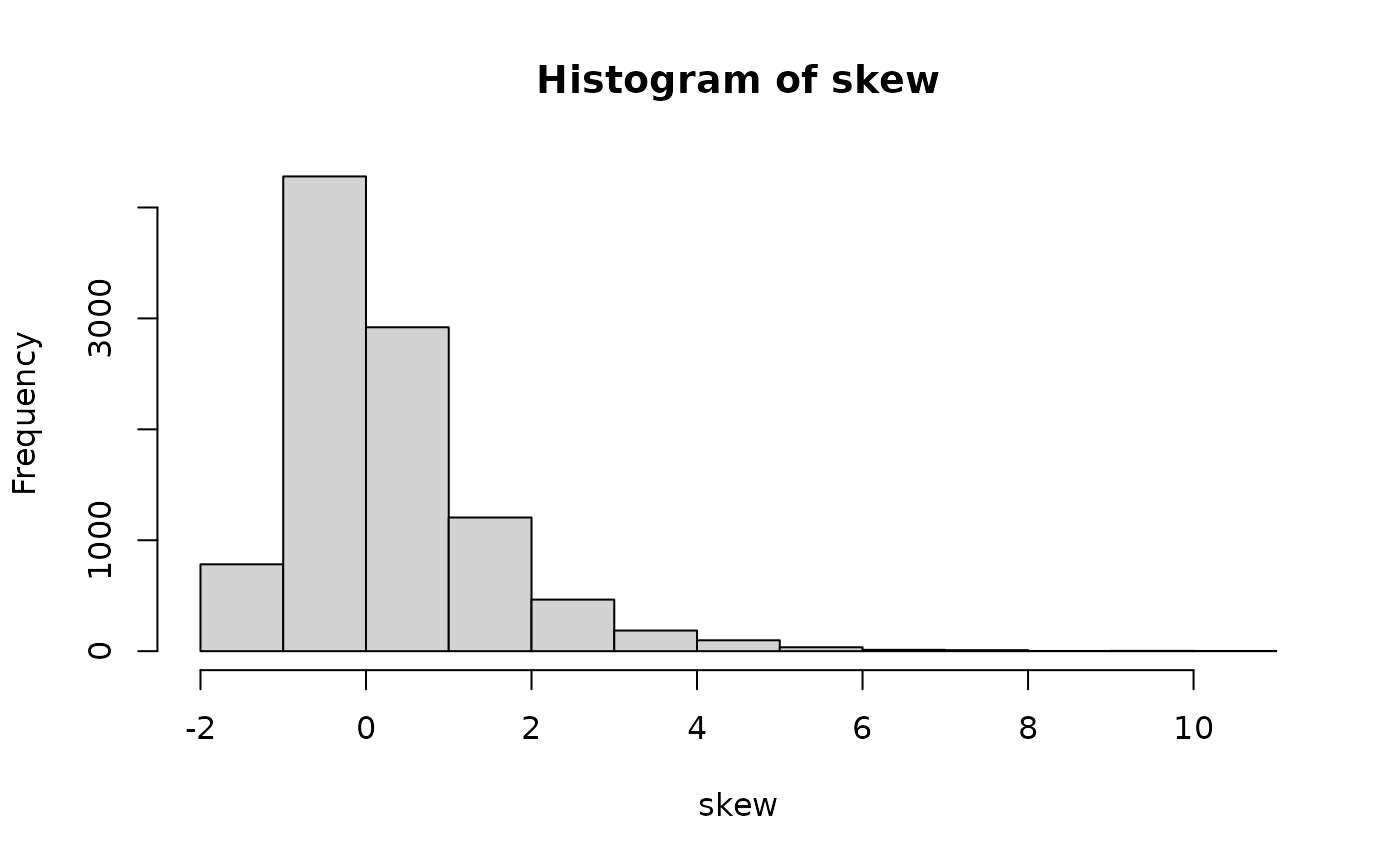
skew <- rmgh(10000,1/2,0)
hist(skew)


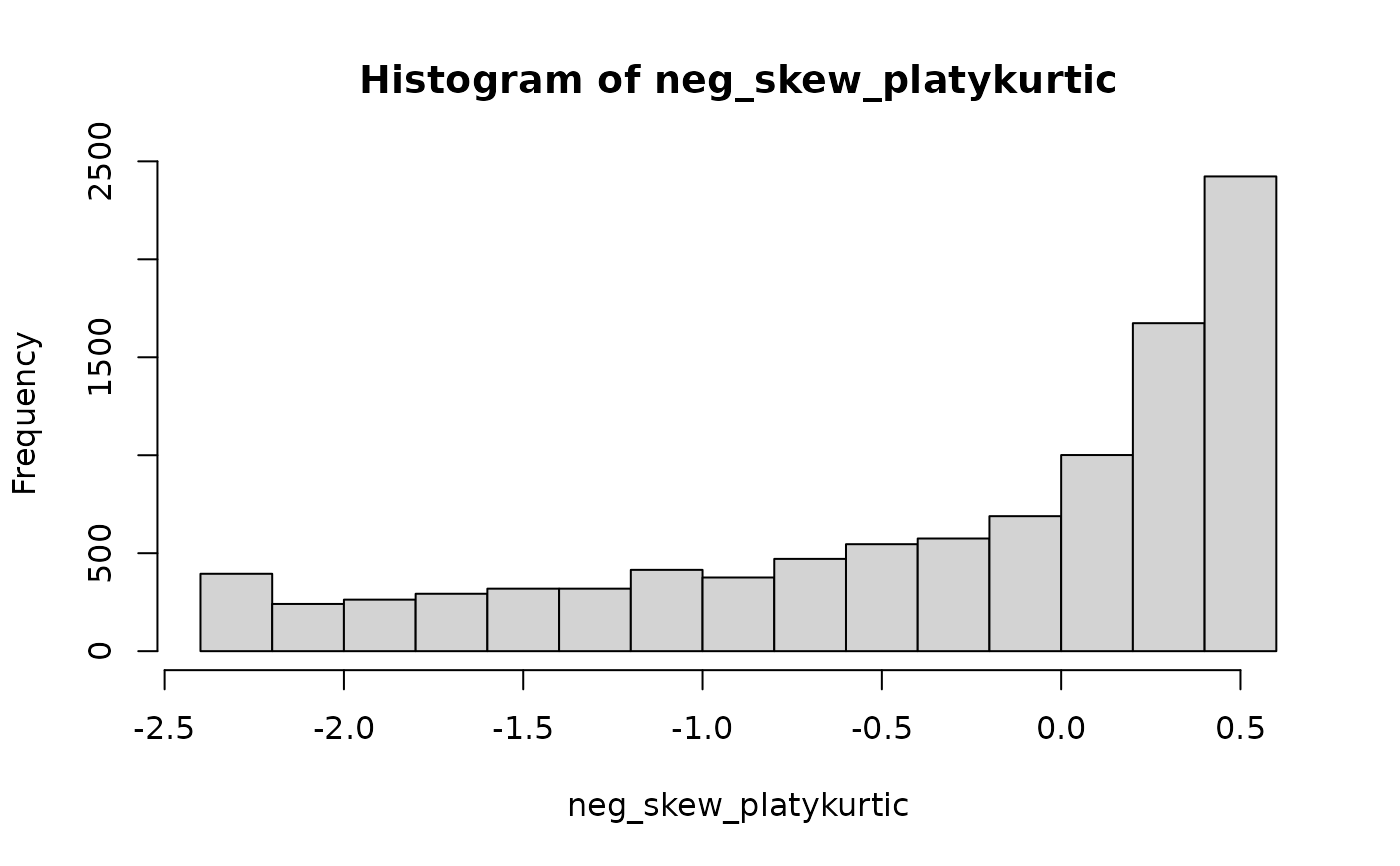
neg_skew_platykurtic <- rmgh(10000,-1,-1/2)
hist(neg_skew_platykurtic)


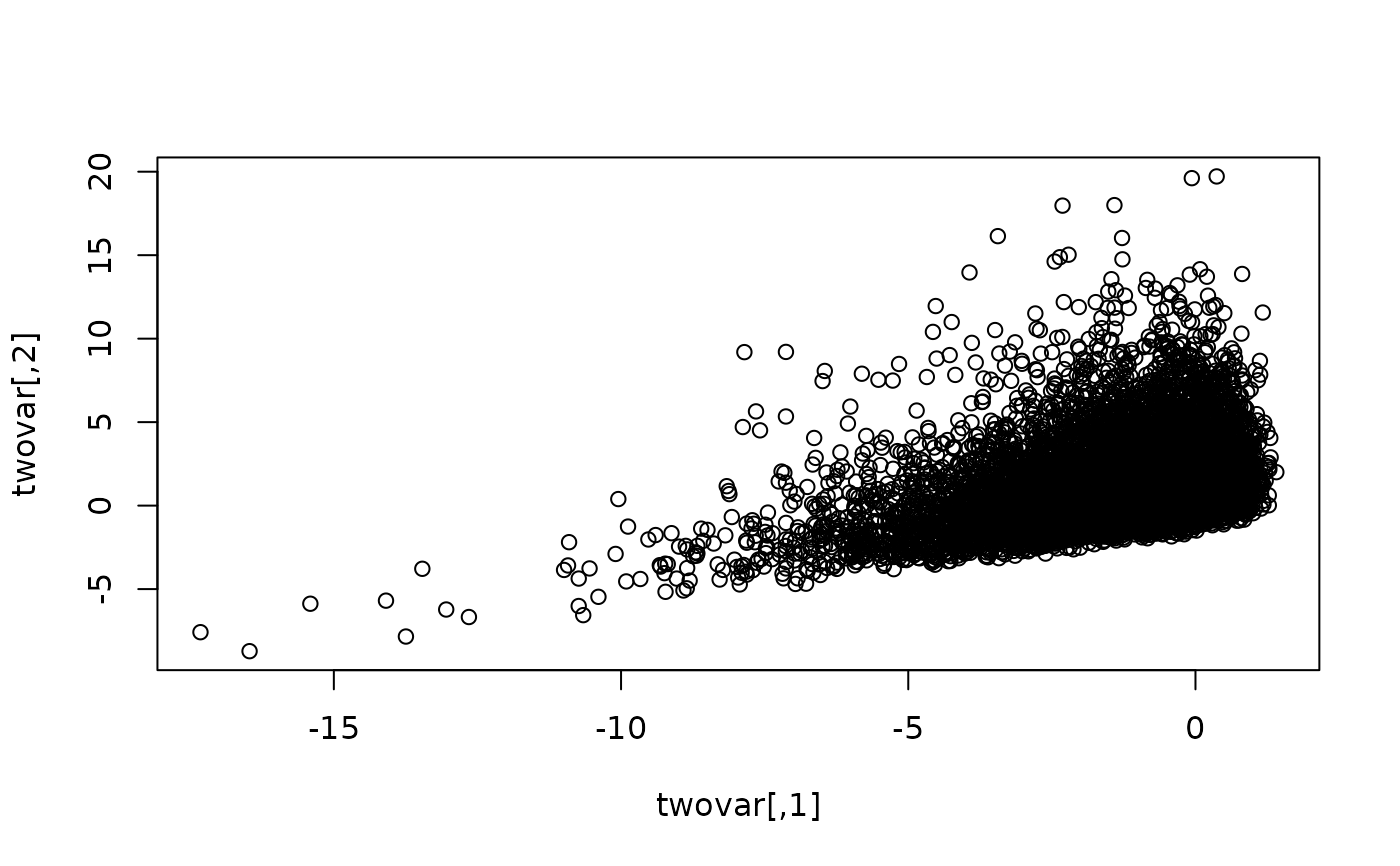
# multivariate
sigma <- matrix(c(2,1,1,4), 2)
mean <- c(-1, 1)
twovar <- rmgh(10000, c(-1/2, 1/2), c(0,0),
    mean=mean, sigma=sigma)
hist(twovar[,1])

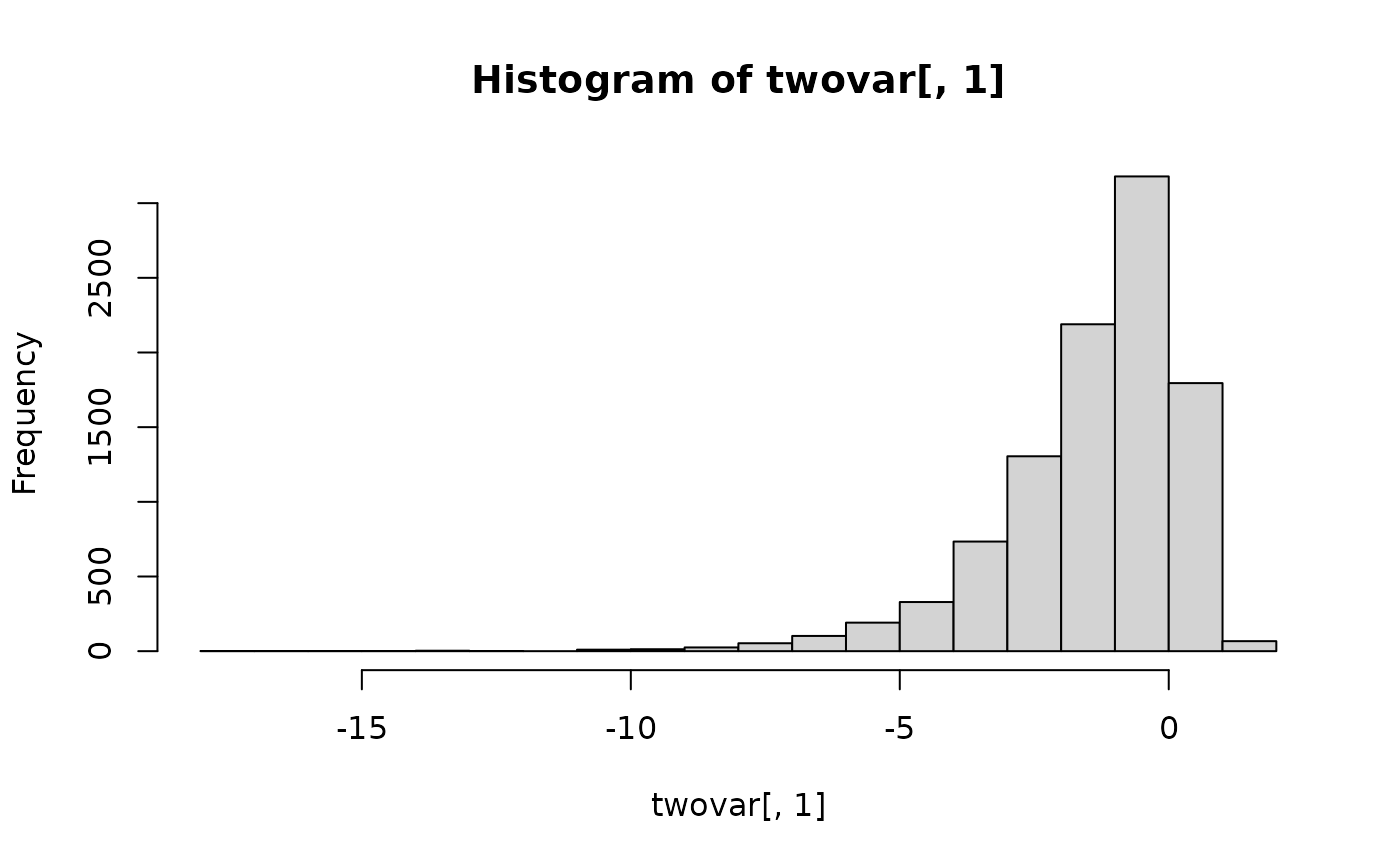hist(twovar[,2])

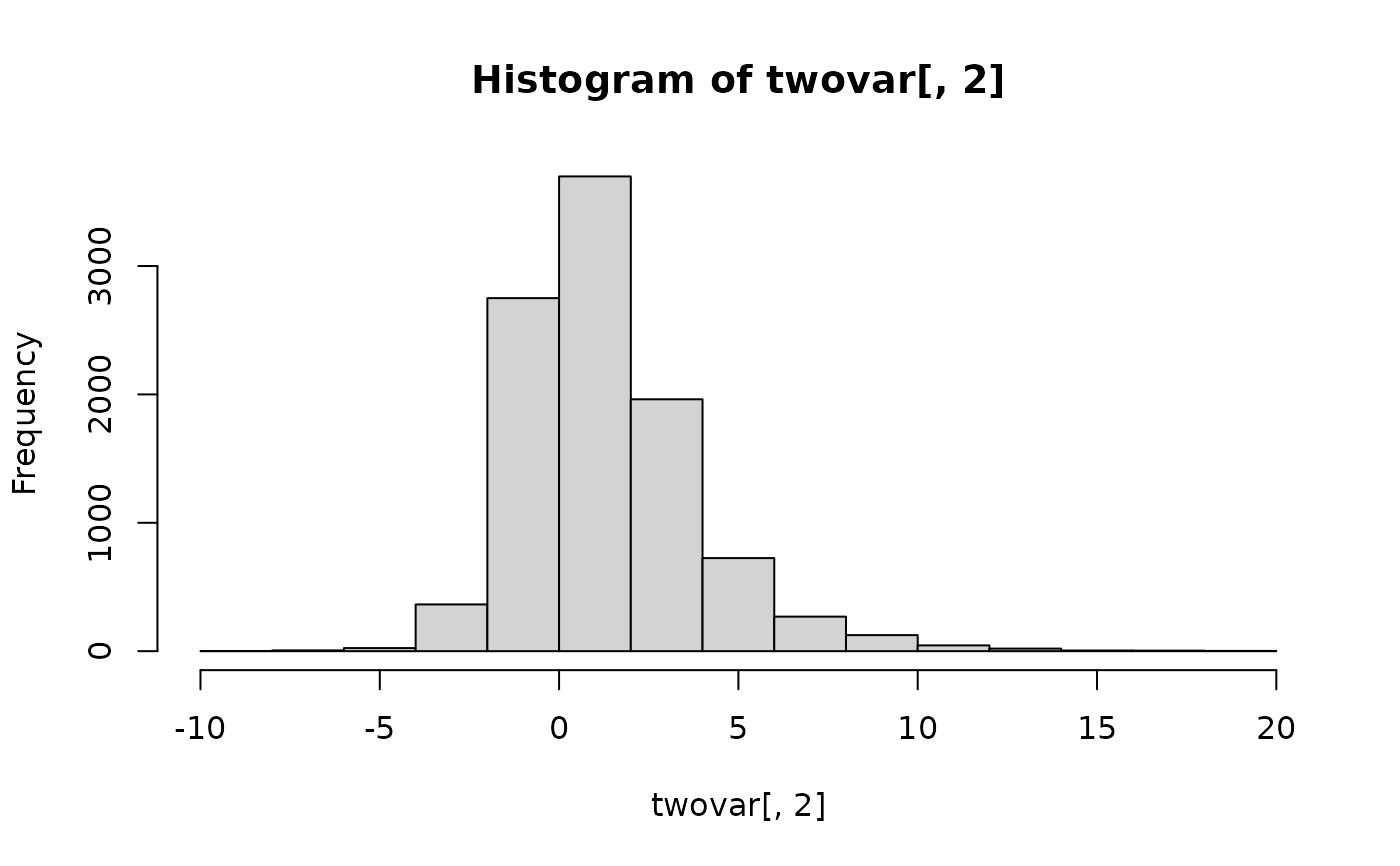plot(twovar)