This function runs the Wald and likelihood-ratio approaches for testing differential
item functioning (DIF) with two or more groups. This is primarily a convenience wrapper to the
multipleGroup function for performing standard DIF procedures. Independent
models can be estimated in parallel by defining a parallel object with mirtCluster,
which will help to decrease the run time. For best results, the baseline model should contain
a set of 'anchor' items and have freely estimated hyper-parameters in the focal groups.
Usage
DIF(
MGmodel,
which.par,
scheme = "add",
items2test = 1:extract.mirt(MGmodel, "nitems"),
groups2test = "all",
seq_stat = "SABIC",
Wald = FALSE,
p.adjust = "none",
pairwise = FALSE,
return_models = FALSE,
return_seq_model = FALSE,
max_run = Inf,
plotdif = FALSE,
type = "trace",
simplify = TRUE,
verbose = TRUE,
...
)Arguments
- MGmodel
an object returned from
multipleGroupto be used as the reference model- which.par
a character vector containing the parameter names which will be inspected for DIF
- scheme
type of DIF analysis to perform, either by adding or dropping constraints across groups. These can be:
- 'add'
parameters in
which.parwill be constrained each item one at a time for items that are specified initems2test. This is beneficial when examining DIF from a model with parameters freely estimated across groups, and when inspecting differences via the Wald test- 'drop'
parameters in
which.parwill be freely estimated for items that are specified initems2test. This is useful when supplying an overly restrictive model and attempting to detect DIF with a slightly less restrictive model- 'add_sequential'
sequentially loop over the items being tested, and at the end of the loop treat DIF tests that satisfy the
seq_statcriteria as invariant. The loop is then re-run on the remaining invariant items to determine if they are now displaying DIF in the less constrained model, and when no new invariant item is found the algorithm stops and returns the items that displayed DIF. Note that the DIF statistics are relative to this final, less constrained model which includes the DIF effects- 'drop_sequential'
sequentially loop over the items being tested, and at the end of the loop treat items that violate the
seq_statcriteria as demonstrating DIF. The loop is then re-run, leaving the items that previously demonstrated DIF as variable across groups, and the remaining test items that previously showed invariance are re-tested. The algorithm stops when no more items showing DIF are found and returns the items that displayed DIF. Note that the DIF statistics are relative to this final, less constrained model which includes the DIF effects
- items2test
a numeric vector, or character vector containing the item names, indicating which items will be tested for DIF. In models where anchor items are known, omit them from this vector. For example, if items 1 and 2 are anchors in a 10 item test, then
items2test = 3:10would work for testing the remaining items (important to remember when using sequential schemes)- groups2test
a character vector indicating which groups to use in the DIF testing investigations. Default is
'all', which uses all group information to perform joint hypothesis tests of DIF (for a two group setup these result in pair-wise tests). For example, if the group names were 'g1', 'g2' and 'g3', and DIF was only to be investigated between group 'g1' and 'g3' then passgroups2test = c('g1', 'g3')- seq_stat
select a statistic to test for in the sequential schemes. Potential values are (in descending order of power)
'AIC','SABIC','HQ', and'BIC'. If a numeric value is input that ranges between 0 and 1, the 'p' value will be tested (e.g.,seq_stat = .05will test for the difference of p < .05 in the add scheme, or p > .05 in the drop scheme), along with the specifiedp.adjustinput- Wald
logical; perform Wald tests for DIF instead of likelihood ratio test?
- p.adjust
string to be passed to the
p.adjustfunction to adjust p-values. Adjustments are located in theadj_pelement in the returned list- pairwise
logical; perform pairwise tests between groups when the number of groups is greater than 2? Useful as quickly specified post-hoc tests
- return_models
logical; return estimated model objects for further analysis? Default is FALSE
- return_seq_model
logical; on the last iteration of the sequential schemes, return the fitted multiple-group model containing the freely estimated parameters indicative of DIF? This is generally only useful when
scheme = 'add_sequential'. Default is FALSE- max_run
a number indicating the maximum number of cycles to perform in sequential searches. The default is to perform search until no further DIF is found
- plotdif
logical; create item plots for items that are displaying DIF according to the
seq_statcriteria? Only available for 'add' type schemes- type
the
typeof plot argument passed toplot(). Default is 'trace', though another good option is 'infotrace'. For ease of viewing, thefacet_itemargument to mirt'splot()function is set toTRUE- simplify
logical; simplify the output by returning a data.frame object with the differences between AIC, BIC, etc, as well as the chi-squared test (X2) and associated df and p-values
- verbose
logical print extra information to the console?
- ...
additional arguments to be passed to
multipleGroupandplot
Value
a mirt_df object with the information-based criteria for DIF, though this may be changed
to a list output when return_models or simplify are modified. As well, a silent
'DIF_coefficeints' attribute is included to view the item parameter differences
between the groups
Details
Generally, the pre-computed baseline model should have been configured with two estimation properties: 1) a set of 'anchor' items, where the anchor items have various parameters that have been constrained to be equal across the groups, and 2) contain freely estimated latent mean and variance terms in all but one group (the so-called 'reference' group). These two properties help to fix the metric of the groups so that item parameter estimates do not contain latent distribution characteristics.
References
Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06
Chalmers, R. P., Counsell, A., and Flora, D. B. (2016). It might not make a big DIF: Improved Differential Test Functioning statistics that account for sampling variability. Educational and Psychological Measurement, 76, 114-140. doi:10.1177/0013164415584576
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
# \donttest{
# simulate data where group 2 has a smaller slopes and more extreme intercepts
set.seed(12345)
a1 <- a2 <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d1 <- d2 <- matrix(rnorm(15,0,.7),ncol=1)
a2[1:2, ] <- a1[1:2, ]/3
d1[c(1,3), ] <- d2[c(1,3), ]/4
head(data.frame(a.group1 = a1, a.group2 = a2, d.group1 = d1, d.group2 = d2))
#> a.group1 a.group2 d.group1 d.group2
#> 1 1.1756586 0.3918862 0.14295747 0.5718299
#> 2 1.2128398 0.4042799 -0.62045026 -0.6204503
#> 3 0.9672090 0.9672090 -0.05802608 -0.2321043
#> 4 0.8639508 0.8639508 0.78449886 0.7844989
#> 5 1.1817662 1.1817662 0.20910659 0.2091066
#> 6 0.4546132 0.4546132 0.54573535 0.5457353
itemtype <- rep('2PL', nrow(a1))
N <- 1000
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = .1, sigma = matrix(1.5))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
#### no anchors, all items tested for DIF by adding item constrains one item at a time.
# define a parallel cluster (optional) to help speed up internal functions
if(interactive()) mirtCluster()
# Information matrix with Oakes' identity (not controlling for latent group differences)
# NOTE: Without properly equating the groups the following example code is not testing for DIF,
# but instead reflects a combination of DIF + latent-trait distribution effects
model <- multipleGroup(dat, 1, group, SE = TRUE)
# Likelihood-ratio test for DIF (as well as model information)
dif <- DIF(model, c('a1', 'd'))
#> NOTE: No hyper-parameters were estimated in the DIF model.
#> For effective DIF testing, freeing the focal group hyper-parameters is recommended.
dif
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -34.621 -29.773 -30.507 -23.419 38.621 2 0
#> Item_2 D1,D2 TRUE -20.364 -15.516 -16.251 -9.162 24.364 2 0
#> Item_3 D1,D2 TRUE -10.101 -5.253 -5.988 1.101 14.101 2 0.001
#> Item_4 D1,D2 TRUE -0.356 4.492 3.757 10.846 4.356 2 0.113
#> Item_5 D1,D2 TRUE 0.968 5.815 5.081 12.169 3.032 2 0.22
#> Item_6 D1,D2 TRUE 3.441 8.289 7.554 14.643 0.559 2 0.756
#> Item_7 D1,D2 TRUE 3.340 8.188 7.453 14.542 0.66 2 0.719
#> Item_8 D1,D2 TRUE -2.371 2.477 1.742 8.831 6.371 2 0.041
#> Item_9 D1,D2 TRUE 0.546 5.393 4.659 11.748 3.454 2 0.178
#> Item_10 D1,D2 TRUE 3.215 8.062 7.328 14.416 0.785 2 0.675
#> Item_11 D1,D2 TRUE -4.853 -0.006 -0.740 6.348 8.853 2 0.012
#> Item_12 D1,D2 TRUE 1.497 6.345 5.610 12.699 2.503 2 0.286
#> Item_13 D1,D2 TRUE 1.854 6.702 5.967 13.056 2.146 2 0.342
#> Item_14 D1,D2 TRUE -4.350 0.498 -0.237 6.852 8.35 2 0.015
#> Item_15 D1,D2 TRUE 3.831 8.679 7.944 15.033 0.169 2 0.919
# function silently includes "DIF_coefficients" attribute to view
# the IRT parameters post-completion
extract.mirt(dif, "DIF_coefficients")
#> $Item_1
#> a1 d g u
#> D1 0.7472578 0.3483822 0 1
#> D2 0.7472578 0.3483822 0 1
#>
#> $Item_2
#> a1 d g u
#> D1 0.8277687 -0.6535244 0 1
#> D2 0.8277687 -0.6535244 0 1
#>
#> $Item_3
#> a1 d g u
#> D1 1.213165 -0.1452843 0 1
#> D2 1.213165 -0.1452843 0 1
#>
#> $Item_4
#> a1 d g u
#> D1 1.017216 0.9327436 0 1
#> D2 1.017216 0.9327436 0 1
#>
#> $Item_5
#> a1 d g u
#> D1 1.216819 0.1966309 0 1
#> D2 1.216819 0.1966309 0 1
#>
#> $Item_6
#> a1 d g u
#> D1 0.5196433 0.652555 0 1
#> D2 0.5196433 0.652555 0 1
#>
#> $Item_7
#> a1 d g u
#> D1 1.348864 1.016455 0 1
#> D2 1.348864 1.016455 0 1
#>
#> $Item_8
#> a1 d g u
#> D1 1.089472 -0.3447219 0 1
#> D2 1.089472 -0.3447219 0 1
#>
#> $Item_9
#> a1 d g u
#> D1 0.993117 -1.006033 0 1
#> D2 0.993117 -1.006033 0 1
#>
#> $Item_10
#> a1 d g u
#> D1 0.791053 -1.099697 0 1
#> D2 0.791053 -1.099697 0 1
#>
#> $Item_11
#> a1 d g u
#> D1 1.053996 1.235564 0 1
#> D2 1.053996 1.235564 0 1
#>
#> $Item_12
#> a1 d g u
#> D1 1.593305 -0.1832728 0 1
#> D2 1.593305 -0.1832728 0 1
#>
#> $Item_13
#> a1 d g u
#> D1 1.389336 0.4619023 0 1
#> D2 1.389336 0.4619023 0 1
#>
#> $Item_14
#> a1 d g u
#> D1 1.294955 0.4870637 0 1
#> D2 1.294955 0.4870637 0 1
#>
#> $Item_15
#> a1 d g u
#> D1 0.8797218 -0.04575426 0 1
#> D2 0.8797218 -0.04575426 0 1
#>
# same as above, but using Wald tests with Benjamini & Hochberg adjustment
DIF(model, c('a1', 'd'), Wald = TRUE, p.adjust = 'fdr')
#> NOTE: No hyper-parameters were estimated in the DIF model.
#> For effective DIF testing, freeing the focal group hyper-parameters is recommended.
#> groups W df p adj_p
#> Item_1 D1,D2 36.513 2 0 0.000
#> Item_2 D1,D2 22.089 2 0 0.000
#> Item_3 D1,D2 13.444 2 0.001 0.006
#> Item_4 D1,D2 4.293 2 0.117 0.251
#> Item_5 D1,D2 3.009 2 0.222 0.370
#> Item_6 D1,D2 0.558 2 0.756 0.810
#> Item_7 D1,D2 0.658 2 0.72 0.810
#> Item_8 D1,D2 6.238 2 0.044 0.111
#> Item_9 D1,D2 3.438 2 0.179 0.336
#> Item_10 D1,D2 0.785 2 0.675 0.810
#> Item_11 D1,D2 8.621 2 0.013 0.050
#> Item_12 D1,D2 2.485 2 0.289 0.433
#> Item_13 D1,D2 2.133 2 0.344 0.469
#> Item_14 D1,D2 8.062 2 0.018 0.053
#> Item_15 D1,D2 0.168 2 0.919 0.919
# equate the groups by assuming the last 5 items have no DIF
itemnames <- colnames(dat)
model <- multipleGroup(dat, 1, group, SE = TRUE,
invariance = c(itemnames[11:ncol(dat)], 'free_means', 'free_var'))
# test whether adding slopes and intercepts constraints results in DIF. Plot items showing DIF
resulta1d <- DIF(model, c('a1', 'd'), plotdif = TRUE, items2test=1:10)
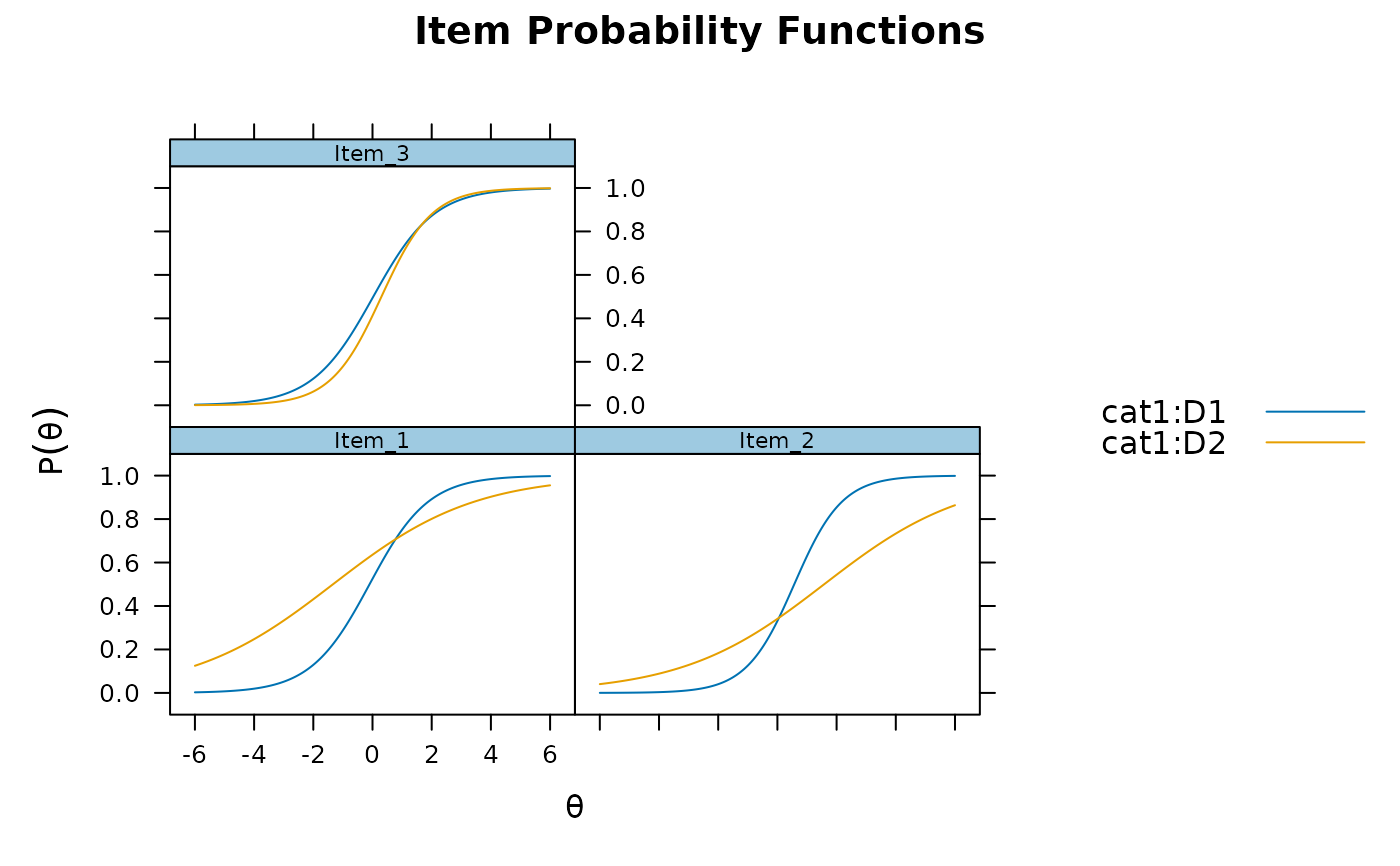resulta1d
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -43.490 -38.642 -39.377 -32.288 47.49 2 0
#> Item_2 D1,D2 TRUE -33.840 -28.993 -29.727 -22.638 37.84 2 0
#> Item_3 D1,D2 TRUE -5.497 -0.649 -1.384 5.705 9.497 2 0.009
#> Item_4 D1,D2 TRUE 2.395 7.242 6.508 13.596 1.605 2 0.448
#> Item_5 D1,D2 TRUE 3.140 7.988 7.253 14.342 0.86 2 0.651
#> Item_6 D1,D2 TRUE 1.122 5.970 5.235 12.324 2.878 2 0.237
#> Item_7 D1,D2 TRUE 3.083 7.931 7.196 14.285 0.917 2 0.632
#> Item_8 D1,D2 TRUE 2.857 7.705 6.970 14.059 1.143 2 0.565
#> Item_9 D1,D2 TRUE 3.674 8.521 7.787 14.875 0.326 2 0.849
#> Item_10 D1,D2 TRUE 3.154 8.001 7.267 14.355 0.846 2 0.655
# test whether adding only slope constraints results in DIF for all items
DIF(model, 'a1', items2test=1:10)
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -20.871 -18.447 -18.815 -15.270 22.871 1 0
#> Item_2 D1,D2 TRUE -34.675 -32.252 -32.619 -29.075 36.675 1 0
#> Item_3 D1,D2 TRUE 0.435 2.859 2.492 6.036 1.565 1 0.211
#> Item_4 D1,D2 TRUE 1.980 4.404 4.036 7.581 0.02 1 0.887
#> Item_5 D1,D2 TRUE 1.754 4.178 3.811 7.355 0.246 1 0.62
#> Item_6 D1,D2 TRUE -0.564 1.860 1.492 5.037 2.564 1 0.109
#> Item_7 D1,D2 TRUE 1.093 3.517 3.150 6.694 0.907 1 0.341
#> Item_8 D1,D2 TRUE 1.431 3.855 3.488 7.032 0.569 1 0.451
#> Item_9 D1,D2 TRUE 1.863 4.287 3.920 7.464 0.137 1 0.712
#> Item_10 D1,D2 TRUE 1.775 4.199 3.832 7.376 0.225 1 0.636
# Determine whether it's a1 or d parameter causing DIF (could be joint, however)
(a1s <- DIF(model, 'a1', items2test = 1:3))
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -20.871 -18.447 -18.815 -15.270 22.871 1 0
#> Item_2 D1,D2 TRUE -34.675 -32.252 -32.619 -29.075 36.675 1 0
#> Item_3 D1,D2 TRUE 0.435 2.859 2.492 6.036 1.565 1 0.211
(ds <- DIF(model, 'd', items2test = 1:3))
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -18.568 -16.145 -16.512 -12.968 20.568 1 0
#> Item_2 D1,D2 TRUE 1.843 4.266 3.899 7.443 0.157 1 0.691
#> Item_3 D1,D2 TRUE -6.229 -3.805 -4.173 -0.628 8.229 1 0.004
### drop down approach (freely estimating parameters across groups) when
### specifying a highly constrained model with estimated latent parameters
model_constrained <- multipleGroup(dat, 1, group,
invariance = c(colnames(dat), 'free_means', 'free_var'))
dropdown <- DIF(model_constrained, c('a1', 'd'), scheme = 'drop')
dropdown
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -43.297 -38.450 -39.184 -32.096 47.297 2 0
#> Item_2 D1,D2 TRUE -32.642 -27.794 -28.529 -21.440 36.642 2 0
#> Item_3 D1,D2 TRUE -10.510 -5.662 -6.397 0.692 14.51 2 0.001
#> Item_4 D1,D2 TRUE 1.885 6.733 5.998 13.087 2.115 2 0.347
#> Item_5 D1,D2 TRUE 3.155 8.003 7.268 14.357 0.845 2 0.655
#> Item_6 D1,D2 TRUE 1.914 6.761 6.027 13.116 2.086 2 0.352
#> Item_7 D1,D2 TRUE 3.887 8.735 8.000 15.089 0.113 2 0.945
#> Item_8 D1,D2 TRUE 0.703 5.550 4.816 11.905 3.297 2 0.192
#> Item_9 D1,D2 TRUE 3.059 7.907 7.172 14.261 0.941 2 0.625
#> Item_10 D1,D2 TRUE 3.631 8.479 7.744 14.833 0.369 2 0.832
#> Item_11 D1,D2 TRUE -0.765 4.083 3.348 10.437 4.765 2 0.092
#> Item_12 D1,D2 TRUE 3.511 8.359 7.624 14.713 0.489 2 0.783
#> Item_13 D1,D2 TRUE 3.416 8.263 7.529 14.618 0.584 2 0.747
#> Item_14 D1,D2 TRUE -0.690 4.157 3.423 10.511 4.69 2 0.096
#> Item_15 D1,D2 TRUE 3.599 8.447 7.712 14.801 0.401 2 0.818
# View silent "DIF_coefficients" attribute
extract.mirt(dropdown, "DIF_coefficients")
#> $Item_1
#> a1 d g u
#> D1 1.0070333 0.1008689 0 1
#> D2 0.4519451 0.5696948 0 1
#>
#> $Item_2
#> a1 d g u
#> D1 1.2404964 -0.7051772 0 1
#> D2 0.4454868 -0.6639707 0 1
#>
#> $Item_3
#> a1 d g u
#> D1 0.9753304 -0.02503532 0 1
#> D2 1.3391630 -0.38511564 0 1
#>
#> $Item_4
#> a1 d g u
#> D1 0.8791819 0.8382862 0 1
#> D2 1.0156000 0.9950612 0 1
#>
#> $Item_5
#> a1 d g u
#> D1 1.121611 0.1289459 0 1
#> D2 1.174548 0.2229440 0 1
#>
#> $Item_6
#> a1 d g u
#> D1 0.5623518 0.6822046 0 1
#> D2 0.4157185 0.6026837 0 1
#>
#> $Item_7
#> a1 d g u
#> D1 1.283799 1.0057393 0 1
#> D2 1.237164 0.9681297 0 1
#>
#> $Item_8
#> a1 d g u
#> D1 0.8938398 -0.3260637 0 1
#> D2 1.1477262 -0.4254126 0 1
#>
#> $Item_9
#> a1 d g u
#> D1 0.8827366 -1.0565622 0 1
#> D2 0.9625327 -0.9928805 0 1
#>
#> $Item_10
#> a1 d g u
#> D1 0.733522 -1.085299 0 1
#> D2 0.745690 -1.154239 0 1
#>
#> $Item_11
#> a1 d g u
#> D1 0.8342627 1.189315 0 1
#> D2 1.1656517 1.241327 0 1
#>
#> $Item_12
#> a1 d g u
#> D1 1.476098 -0.2510170 0 1
#> D2 1.492368 -0.1715056 0 1
#>
#> $Item_13
#> a1 d g u
#> D1 1.236010 0.4387954 0 1
#> D2 1.358438 0.4178786 0 1
#>
#> $Item_14
#> a1 d g u
#> D1 1.042359 0.4541499 0 1
#> D2 1.400256 0.4556638 0 1
#>
#> $Item_15
#> a1 d g u
#> D1 0.8583058 -0.06114579 0 1
#> D2 0.7771780 -0.06825570 0 1
#>
### sequential schemes (add constraints)
### sequential searches using SABIC as the selection criteria
# starting from completely different models
stepup <- DIF(model, c('a1', 'd'), scheme = 'add_sequential',
items2test=1:10)
#>
Checking for DIF in 3 more items
#> Computing final DIF estimates...
stepup
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -43.161 -38.314 -39.048 -31.959 47.161 2 0
#> Item_2 D1,D2 TRUE -34.224 -29.377 -30.111 -23.022 38.224 2 0
#> Item_3 D1,D2 TRUE -7.368 -2.520 -3.255 3.834 11.368 2 0.003
# step down procedure for highly constrained model
stepdown <- DIF(model_constrained, c('a1', 'd'), scheme = 'drop_sequential')
#>
Checking for DIF in 12 more items
#> Computing final DIF estimates...
stepdown
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 D1,D2 TRUE -43.161 -38.314 -39.048 -31.959 47.161 2 0
#> Item_2 D1,D2 TRUE -34.224 -29.377 -30.111 -23.022 38.224 2 0
#> Item_3 D1,D2 TRUE -7.368 -2.520 -3.255 3.834 11.368 2 0.003
# view final MG model (only useful when scheme is 'add_sequential')
updated_mod <- DIF(model, c('a1', 'd'), scheme = 'add_sequential',
return_seq_model=TRUE)
#>
Checking for DIF in 3 more items
#> Computing final DIF estimates...
plot(updated_mod, type='trace')
###################################
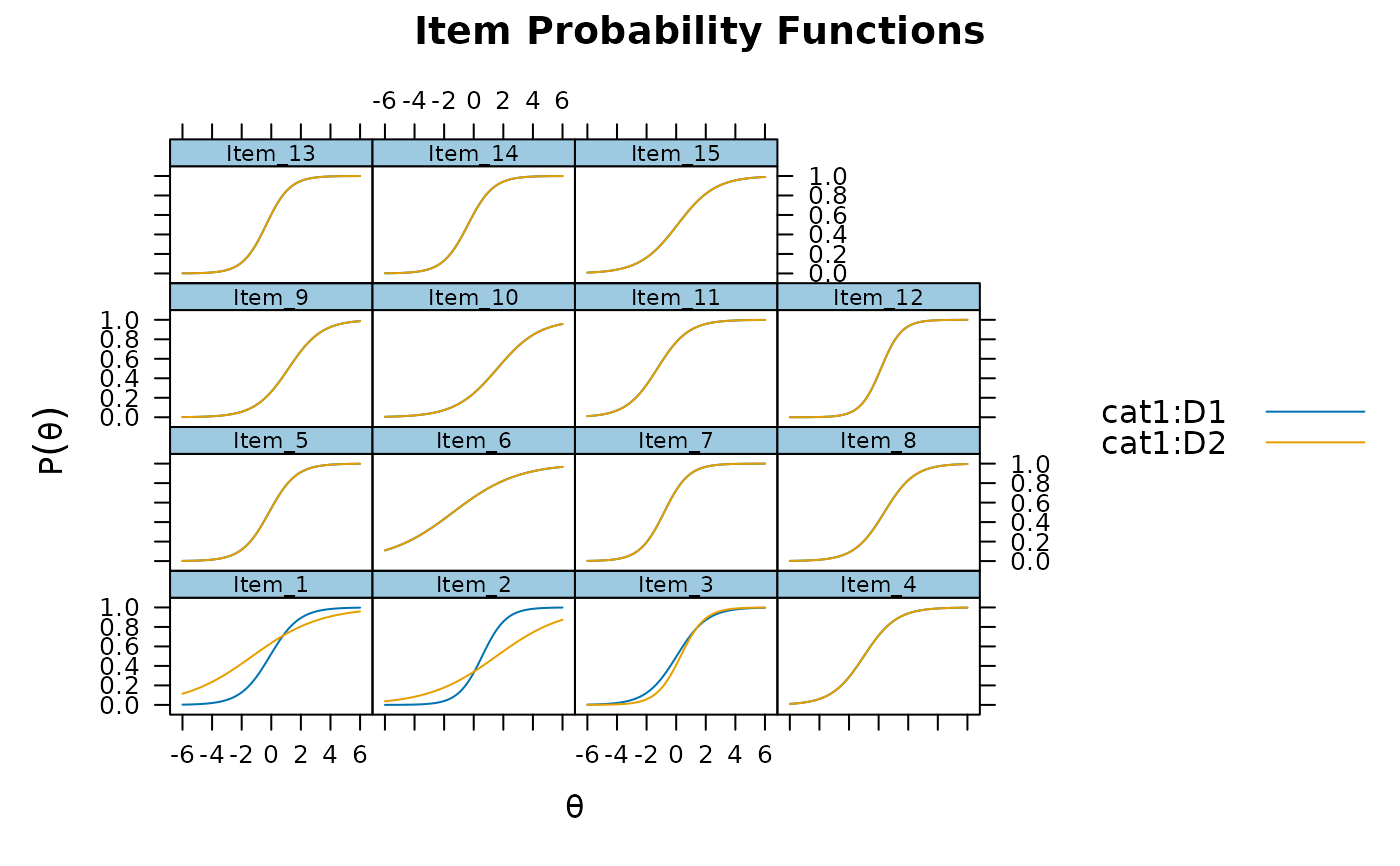# Multi-group example
a1 <- a2 <- a3 <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d1 <- d2 <- d3 <- matrix(rnorm(15,0,.7),ncol=1)
a2[1:2, ] <- a1[1:2, ]/3
d3[c(1,3), ] <- d2[c(1,3), ]/4
head(data.frame(a.group1 = a1, a.group2 = a2, a.group3 = a3,
d.group1 = d1, d.group2 = d2, d.group3 = d3))
#> a.group1 a.group2 a.group3 d.group1 d.group2 d.group3
#> 1 0.9921262 0.3307087 0.9921262 -0.6923662 -0.6923662 -0.1730916
#> 2 0.6115843 0.2038614 0.6115843 -0.4398444 -0.4398444 -0.4398444
#> 3 1.0571399 1.0571399 1.0571399 0.5243734 0.5243734 0.1310934
#> 4 1.1508422 1.1508422 1.1508422 -1.0133952 -1.0133952 -1.0133952
#> 5 1.2447020 1.2447020 1.2447020 -0.4542548 -0.4542548 -0.4542548
#> 6 0.6518627 0.6518627 0.6518627 0.7766470 0.7766470 0.7766470
itemtype <- rep('2PL', nrow(a1))
N <- 1000
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = .1, sigma = matrix(1.5))
dataset3 <- simdata(a3, d3, N, itemtype, mu = .2)
dat <- rbind(dataset1, dataset2, dataset3)
group <- gl(3, N, labels = c('g1', 'g2', 'g3'))
# equate the groups by assuming the last 5 items have no DIF
itemnames <- colnames(dat)
model <- multipleGroup(dat, group=group, SE=TRUE,
invariance = c(itemnames[11:ncol(dat)], 'free_means', 'free_var'))
coef(model, simplify=TRUE)
#> $g1
#> $items
#> a1 d g u
#> Item_1 0.982 -0.707 0 1
#> Item_2 0.571 -0.458 0 1
#> Item_3 0.991 0.557 0 1
#> Item_4 1.240 -1.133 0 1
#> Item_5 1.095 -0.475 0 1
#> Item_6 0.711 0.712 0 1
#> Item_7 0.952 -1.641 0 1
#> Item_8 0.709 -0.568 0 1
#> Item_9 1.131 0.736 0 1
#> Item_10 1.211 0.397 0 1
#> Item_11 1.089 -0.384 0 1
#> Item_12 0.523 -1.044 0 1
#> Item_13 0.983 0.345 0 1
#> Item_14 0.950 0.330 0 1
#> Item_15 1.292 -0.246 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $g2
#> $items
#> a1 d g u
#> Item_1 0.286 -0.788 0 1
#> Item_2 0.080 -0.397 0 1
#> Item_3 0.898 0.505 0 1
#> Item_4 1.025 -0.994 0 1
#> Item_5 1.023 -0.364 0 1
#> Item_6 0.717 0.832 0 1
#> Item_7 1.100 -1.903 0 1
#> Item_8 0.783 -0.487 0 1
#> Item_9 0.956 0.820 0 1
#> Item_10 1.095 0.428 0 1
#> Item_11 1.089 -0.384 0 1
#> Item_12 0.523 -1.044 0 1
#> Item_13 0.983 0.345 0 1
#> Item_14 0.950 0.330 0 1
#> Item_15 1.292 -0.246 0 1
#>
#> $means
#> F1
#> 0.038
#>
#> $cov
#> F1
#> F1 1.653
#>
#>
#> $g3
#> $items
#> a1 d g u
#> Item_1 1.029 -0.180 0 1
#> Item_2 0.766 -0.442 0 1
#> Item_3 1.175 0.171 0 1
#> Item_4 1.319 -1.101 0 1
#> Item_5 1.345 -0.567 0 1
#> Item_6 0.620 0.694 0 1
#> Item_7 1.073 -1.699 0 1
#> Item_8 0.842 -0.678 0 1
#> Item_9 1.227 0.945 0 1
#> Item_10 1.344 0.540 0 1
#> Item_11 1.089 -0.384 0 1
#> Item_12 0.523 -1.044 0 1
#> Item_13 0.983 0.345 0 1
#> Item_14 0.950 0.330 0 1
#> Item_15 1.292 -0.246 0 1
#>
#> $means
#> F1
#> 0.189
#>
#> $cov
#> F1
#> F1 0.893
#>
#>
# omnibus tests
dif <- DIF(model, which.par = c('a1', 'd'), items2test=1:9)
dif
#> groups converged AIC SABIC HQ BIC X2 df p
#> Item_1 g1,g2,g3 TRUE -100.312 -88.996 -91.670 -76.286 108.312 4 0
#> Item_2 g1,g2,g3 TRUE -39.696 -28.380 -31.054 -15.670 47.696 4 0
#> Item_3 g1,g2,g3 TRUE -8.644 2.672 -0.002 15.382 16.644 4 0.002
#> Item_4 g1,g2,g3 TRUE 4.559 15.875 13.201 28.584 3.441 4 0.487
#> Item_5 g1,g2,g3 TRUE 3.087 14.402 11.728 27.112 4.913 4 0.296
#> Item_6 g1,g2,g3 TRUE 5.556 16.872 14.198 29.581 2.444 4 0.655
#> Item_7 g1,g2,g3 TRUE 4.844 16.160 13.486 28.869 3.156 4 0.532
#> Item_8 g1,g2,g3 TRUE 4.504 15.819 13.145 28.529 3.496 4 0.478
#> Item_9 g1,g2,g3 TRUE 2.263 13.578 10.904 26.288 5.737 4 0.22
# pairwise post-hoc tests for items flagged via omnibus tests
dif.posthoc <- DIF(model, which.par = c('a1', 'd'), items2test=1:2,
pairwise = TRUE)
dif.posthoc
#> item groups converged AIC SABIC HQ BIC X2 df p
#> 1 Item_1 g1,g2 TRUE -32.488 -26.830 -28.167 -20.475 36.488 2 0
#> 2 Item_2 g1,g2 TRUE -19.000 -13.342 -14.679 -6.988 23 2 0
#> 3 Item_1 g1,g3 TRUE -19.543 -13.885 -15.222 -7.530 23.543 2 0
#> 4 Item_2 g1,g3 TRUE 1.728 7.385 6.048 13.740 2.272 2 0.321
#> 5 Item_1 g2,g3 TRUE -90.300 -84.642 -85.979 -78.287 94.3 2 0
#> 6 Item_2 g2,g3 TRUE -36.756 -31.098 -32.435 -24.743 40.756 2 0
# further probing for df = 1 tests, this time with Wald tests
DIF(model, which.par = c('a1'), items2test=1:2, pairwise = TRUE,
Wald=TRUE)
#> item groups W df p
#> 1 Item_1 g1,g2 29.897 1 0
#> 2 Item_2 g1,g2 22.022 1 0
#> 3 Item_1 g1,g3 0.076 1 0.783
#> 4 Item_2 g1,g3 1.939 1 0.164
#> 5 Item_1 g2,g3 27.618 1 0
#> 6 Item_2 g2,g3 30.587 1 0
DIF(model, which.par = c('d'), items2test=1:2, pairwise = TRUE,
Wald=TRUE)
#> item groups W df p
#> 1 Item_1 g1,g2 0.592 1 0.442
#> 2 Item_2 g1,g2 0.419 1 0.518
#> 3 Item_1 g1,g3 21.130 1 0
#> 4 Item_2 g1,g3 0.025 1 0.874
#> 5 Item_1 g2,g3 29.742 1 0
#> 6 Item_2 g2,g3 0.182 1 0.669
# }