multipleGroup performs a full-information
maximum-likelihood multiple group analysis for any combination of dichotomous and polytomous
data under the item response theory paradigm using either Cai's (2010)
Metropolis-Hastings Robbins-Monro (MHRM) algorithm or with an EM algorithm approach. This
function may be used for detecting differential item functioning (DIF), thought the
DIF function may provide a more convenient approach. If the grouping
variable is not specified then the dentype input can be modified to fit
mixture models to estimate any latent group components.
Usage
multipleGroup(
data,
model = 1,
group,
itemtype = NULL,
invariance = "",
method = "EM",
dentype = "Gaussian",
itemdesign = NULL,
item.formula = NULL,
...
)Arguments
- data
a
matrixordata.framethat consists of numerically ordered data, organized in the form of integers, with missing data coded asNA- model
string to be passed to, or a model object returned from,
mirt.modeldeclaring how the global model is to be estimated (useful to apply constraints here)- group
a
characterorfactorvector indicating group membership. If acharactervector is supplied this will be automatically transformed into afactorvariable. As well, the first level of the (factorized) grouping variable will be treated as the "reference" group- itemtype
can be same type of input as is documented in
mirt, however may also be angroupsbynitemsmatrix specifying the type of IRT models for each group, respectively. Rows of this input correspond to the levels of thegroupinput. For mixture models the rows correspond to the respective mixture grouping variables to be constructed, and the IRT models should be within these mixtures- invariance
a character vector containing the following possible options:
'free_mean'or'free_means'freely estimate all latent means in all focal groups (reference group constrained to a vector of 0's)
'free_var','free_vars','free_variance', or'free_variances'freely estimate all latent variances in focal groups (reference group variances all constrained to 1)
'slopes'to constrain all the slopes to be equal across all groups
'intercepts'to constrain all the intercepts to be equal across all groups, note for nominal models this also includes the category specific slope parameters
Additionally, specifying specific item name bundles (from
colnames(data)) will constrain all freely estimated parameters in each item to be equal across groups. This is useful for selecting 'anchor' items for vertical and horizontal scaling, and for detecting differential item functioning (DIF) across groups- method
a character object that is either
'EM','QMCEM', or'MHRM'(default is'EM'). Seemirtfor details- dentype
type of density form to use for the latent trait parameters. Current options include all of the methods described in
mirt, as well as'mixture-#'estimates mixtures of Gaussian distributions, where the#placeholder represents the number of potential grouping variables (e.g.,'mixture-3'will estimate 3 underlying classes). Each class is assigned the group nameMIXTURE_#, where#is the class number. Note that internally the mixture coefficients are stored as log values where the first mixture group coefficient is fixed at 0
- itemdesign
see
mirtfor details- item.formula
see
mirtfor details- ...
additional arguments to be passed to the estimation engine. See
mirtfor details and examples
Value
function returns an object of class MultipleGroupClass
(MultipleGroupClass-class).
Details
By default the estimation in multipleGroup assumes that the models are maximally
independent, and therefore could initially be performed by sub-setting the data and running
identical models with mirt and aggregating the results (e.g., log-likelihood).
However, constrains may be automatically imposed across groups by invoking various
invariance keywords. Users may also supply a list of parameter equality constraints
to by constrain argument, of define equality constraints using the
mirt.model syntax (recommended).
References
Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29. doi:10.18637/jss.v048.i06
Magnus, B. E. and Garnier-Villarreal (2022). A multidimensional zero-inflated graded response model for ordinal symptom data. Psychological Methods, 27, 261-279.
Wall, M., M., Park, J., Y., and Moustaki I. (2015). IRT modeling in the presence of zero-inflation with application to psychiatric disorder severity. Applied Psychological Measurement 39: 583-597.
See also
mirt, DIF, extract.group, DRF
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
# \donttest{
# single factor
set.seed(12345)
a <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d <- matrix(rnorm(15,0,.7),ncol=1)
itemtype <- rep('2PL', nrow(a))
N <- 1000
dataset1 <- simdata(a, d, N, itemtype)
dataset2 <- simdata(a, d, N, itemtype, mu = .1, sigma = matrix(1.5))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
# marginal information
itemstats(dat)
#> $overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 2000 7.888 3.555 0.188 0.053 0.777 1.678
#>
#> $itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 2000 0.609 0.488 0.525 0.414 0.762
#> Item_2 2000 0.392 0.488 0.540 0.431 0.761
#> Item_3 2000 0.456 0.498 0.526 0.413 0.762
#> Item_4 2000 0.684 0.465 0.461 0.349 0.768
#> Item_5 2000 0.538 0.499 0.528 0.415 0.762
#> Item_6 2000 0.649 0.477 0.334 0.207 0.779
#> Item_7 2000 0.681 0.466 0.524 0.419 0.762
#> Item_8 2000 0.432 0.495 0.504 0.389 0.764
#> Item_9 2000 0.302 0.459 0.446 0.334 0.769
#> Item_10 2000 0.274 0.446 0.388 0.273 0.774
#> Item_11 2000 0.734 0.442 0.457 0.351 0.768
#> Item_12 2000 0.470 0.499 0.585 0.481 0.756
#> Item_13 2000 0.585 0.493 0.561 0.455 0.759
#> Item_14 2000 0.592 0.492 0.538 0.428 0.761
#> Item_15 2000 0.490 0.500 0.458 0.336 0.769
#>
#> $proportions
#> 0 1
#> Item_1 0.392 0.609
#> Item_2 0.608 0.392
#> Item_3 0.544 0.456
#> Item_4 0.316 0.684
#> Item_5 0.462 0.538
#> Item_6 0.351 0.649
#> Item_7 0.318 0.681
#> Item_8 0.569 0.432
#> Item_9 0.698 0.302
#> Item_10 0.726 0.274
#> Item_11 0.266 0.734
#> Item_12 0.530 0.470
#> Item_13 0.416 0.585
#> Item_14 0.408 0.592
#> Item_15 0.509 0.490
#>
# conditional information
itemstats(dat, group=group)
#> $D1
#> $D1$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 1000 7.82 3.346 0.159 0.047 0.74 1.705
#>
#> $D1$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 1000 0.605 0.489 0.484 0.361 0.725
#> Item_2 1000 0.368 0.483 0.507 0.388 0.722
#> Item_3 1000 0.461 0.499 0.471 0.343 0.727
#> Item_4 1000 0.673 0.469 0.439 0.315 0.729
#> Item_5 1000 0.526 0.500 0.500 0.376 0.723
#> Item_6 1000 0.654 0.476 0.355 0.222 0.739
#> Item_7 1000 0.683 0.466 0.508 0.394 0.722
#> Item_8 1000 0.431 0.495 0.462 0.333 0.728
#> Item_9 1000 0.287 0.453 0.419 0.298 0.731
#> Item_10 1000 0.274 0.446 0.372 0.249 0.735
#> Item_11 1000 0.739 0.439 0.401 0.282 0.732
#> Item_12 1000 0.456 0.498 0.563 0.448 0.715
#> Item_13 1000 0.584 0.493 0.535 0.416 0.719
#> Item_14 1000 0.592 0.492 0.483 0.358 0.725
#> Item_15 1000 0.487 0.500 0.451 0.321 0.729
#>
#> $D1$proportions
#> 0 1
#> Item_1 0.395 0.605
#> Item_2 0.632 0.368
#> Item_3 0.539 0.461
#> Item_4 0.327 0.673
#> Item_5 0.474 0.526
#> Item_6 0.346 0.654
#> Item_7 0.317 0.683
#> Item_8 0.569 0.431
#> Item_9 0.713 0.287
#> Item_10 0.726 0.274
#> Item_11 0.261 0.739
#> Item_12 0.544 0.456
#> Item_13 0.416 0.584
#> Item_14 0.408 0.592
#> Item_15 0.513 0.487
#>
#>
#> $D2
#> $D2$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 1000 7.955 3.754 0.217 0.065 0.807 1.65
#>
#> $D2$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 1000 0.612 0.488 0.563 0.464 0.792
#> Item_2 1000 0.417 0.493 0.569 0.469 0.792
#> Item_3 1000 0.450 0.498 0.578 0.479 0.791
#> Item_4 1000 0.695 0.461 0.484 0.381 0.798
#> Item_5 1000 0.551 0.498 0.553 0.451 0.793
#> Item_6 1000 0.644 0.479 0.316 0.195 0.811
#> Item_7 1000 0.680 0.467 0.540 0.443 0.794
#> Item_8 1000 0.432 0.496 0.544 0.440 0.794
#> Item_9 1000 0.317 0.466 0.470 0.365 0.799
#> Item_10 1000 0.275 0.447 0.403 0.297 0.804
#> Item_11 1000 0.729 0.445 0.508 0.413 0.796
#> Item_12 1000 0.483 0.500 0.606 0.511 0.788
#> Item_13 1000 0.585 0.493 0.587 0.491 0.790
#> Item_14 1000 0.591 0.492 0.589 0.493 0.790
#> Item_15 1000 0.494 0.500 0.466 0.351 0.801
#>
#> $D2$proportions
#> 0 1
#> Item_1 0.388 0.612
#> Item_2 0.583 0.417
#> Item_3 0.550 0.450
#> Item_4 0.305 0.695
#> Item_5 0.449 0.551
#> Item_6 0.356 0.644
#> Item_7 0.320 0.680
#> Item_8 0.568 0.432
#> Item_9 0.683 0.317
#> Item_10 0.725 0.275
#> Item_11 0.271 0.729
#> Item_12 0.517 0.483
#> Item_13 0.415 0.585
#> Item_14 0.409 0.591
#> Item_15 0.506 0.494
#>
#>
mod_configural <- multipleGroup(dat, 1, group = group) #completely separate analyses
# limited information fit statistics
M2(mod_configural)
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR.D1 SRMSR.D2
#> stats 142.9866 180 0.9806548 0 0 0 0.02414868 0.01901262
#> TLI CFI
#> stats 1.005381 1
mod_metric <- multipleGroup(dat, 1, group = group, invariance=c('slopes')) #equal slopes
# equal intercepts, free variance and means
mod_scalar2 <- multipleGroup(dat, 1, group = group,
invariance=c('slopes', 'intercepts', 'free_var','free_means'))
mod_scalar1 <- multipleGroup(dat, 1, group = group, #fixed means
invariance=c('slopes', 'intercepts', 'free_var'))
mod_fullconstrain <- multipleGroup(dat, 1, group = group,
invariance=c('slopes', 'intercepts'))
extract.mirt(mod_fullconstrain, 'time') #time of estimation components
#> TOTAL: Data Estep Mstep SE Post
#> 0.395 0.074 0.096 0.207 0.000 0.001
# optionally use Newton-Raphson for (generally) faster convergence in the
# M-step's, though occasionally less stable
mod_fullconstrain <- multipleGroup(dat, 1, group = group, optimizer = 'NR',
invariance=c('slopes', 'intercepts'))
extract.mirt(mod_fullconstrain, 'time') #time of estimation components
#> TOTAL: Data Estep Mstep SE Post
#> 0.267 0.075 0.109 0.064 0.000 0.001
summary(mod_scalar2)
#>
#> ----------
#> GROUP: D1
#> F1 h2
#> Item_1 0.544 0.2962
#> Item_2 0.577 0.3324
#> Item_3 0.529 0.2799
#> Item_4 0.460 0.2118
#> Item_5 0.536 0.2877
#> Item_6 0.253 0.0639
#> Item_7 0.570 0.3247
#> Item_8 0.498 0.2479
#> Item_9 0.459 0.2104
#> Item_10 0.373 0.1393
#> Item_11 0.487 0.2368
#> Item_12 0.632 0.3998
#> Item_13 0.596 0.3547
#> Item_14 0.561 0.3147
#> Item_15 0.414 0.1715
#>
#> SS loadings: 3.872
#> Proportion Var: 0.258
#>
#> Factor correlations:
#>
#> F1
#> F1 1
#>
#> ----------
#> GROUP: D2
#> F1 h2
#> Item_1 0.634 0.4017
#> Item_2 0.665 0.4426
#> Item_3 0.619 0.3827
#> Item_4 0.548 0.3000
#> Item_5 0.626 0.3919
#> Item_6 0.313 0.0981
#> Item_7 0.659 0.4341
#> Item_8 0.587 0.3446
#> Item_9 0.546 0.2983
#> Item_10 0.453 0.2052
#> Item_11 0.575 0.3311
#> Item_12 0.718 0.5152
#> Item_13 0.683 0.4671
#> Item_14 0.650 0.4228
#> Item_15 0.498 0.2483
#>
#> SS loadings: 5.284
#> Proportion Var: 0.352
#>
#> Factor correlations:
#>
#> F1
#> F1 1
coef(mod_scalar2, simplify=TRUE)
#> $D1
#> $items
#> a1 d g u
#> Item_1 1.104 0.538 0 1
#> Item_2 1.201 -0.630 0 1
#> Item_3 1.061 -0.265 0 1
#> Item_4 0.882 0.900 0 1
#> Item_5 1.082 0.164 0 1
#> Item_6 0.445 0.636 0 1
#> Item_7 1.180 0.976 0 1
#> Item_8 0.977 -0.377 0 1
#> Item_9 0.879 -1.035 0 1
#> Item_10 0.685 -1.118 0 1
#> Item_11 0.948 1.213 0 1
#> Item_12 1.389 -0.224 0 1
#> Item_13 1.262 0.429 0 1
#> Item_14 1.153 0.453 0 1
#> Item_15 0.774 -0.070 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $D2
#> $items
#> a1 d g u
#> Item_1 1.104 0.538 0 1
#> Item_2 1.201 -0.630 0 1
#> Item_3 1.061 -0.265 0 1
#> Item_4 0.882 0.900 0 1
#> Item_5 1.082 0.164 0 1
#> Item_6 0.445 0.636 0 1
#> Item_7 1.180 0.976 0 1
#> Item_8 0.977 -0.377 0 1
#> Item_9 0.879 -1.035 0 1
#> Item_10 0.685 -1.118 0 1
#> Item_11 0.948 1.213 0 1
#> Item_12 1.389 -0.224 0 1
#> Item_13 1.262 0.429 0 1
#> Item_14 1.153 0.453 0 1
#> Item_15 0.774 -0.070 0 1
#>
#> $means
#> F1
#> 0.066
#>
#> $cov
#> F1
#> F1 1.595
#>
#>
residuals(mod_scalar2)
#> $D1
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> Item_1 NA -0.036 -0.056 0.036 -0.014 0.014 0.017 -0.020 -0.008 -0.066
#> Item_2 1.305 NA -0.052 -0.032 -0.031 0.033 -0.028 0.034 0.038 0.042
#> Item_3 3.144 2.659 NA -0.047 0.057 0.071 -0.037 -0.050 0.033 -0.047
#> Item_4 1.279 1.041 2.173 NA 0.029 0.035 0.032 -0.039 -0.038 0.032
#> Item_5 0.198 0.932 3.291 0.862 NA 0.029 0.048 -0.028 0.027 -0.027
#> Item_6 0.204 1.059 5.032 1.197 0.830 NA 0.020 0.034 0.023 0.041
#> Item_7 0.277 0.804 1.362 1.018 2.337 0.392 NA -0.023 -0.040 0.038
#> Item_8 0.402 1.143 2.483 1.545 0.774 1.125 0.518 NA -0.027 0.025
#> Item_9 0.067 1.478 1.062 1.471 0.717 0.523 1.631 0.726 NA 0.052
#> Item_10 4.303 1.756 2.228 1.054 0.744 1.649 1.453 0.610 2.692 NA
#> Item_11 0.361 3.951 0.988 1.197 0.910 1.320 0.139 2.072 2.295 1.368
#> Item_12 1.718 0.586 1.038 0.725 0.218 0.454 1.323 0.473 0.322 0.604
#> Item_13 0.194 3.315 1.368 1.158 0.797 0.517 0.045 0.395 0.200 2.690
#> Item_14 0.074 0.804 3.798 2.946 0.648 0.228 0.223 0.463 0.693 0.378
#> Item_15 0.164 1.266 0.869 6.383 4.884 1.982 0.583 1.563 1.130 2.406
#> Item_11 Item_12 Item_13 Item_14 Item_15
#> Item_1 -0.019 0.041 -0.014 -0.009 0.013
#> Item_2 -0.063 0.024 0.058 0.028 0.036
#> Item_3 -0.031 0.032 -0.037 -0.062 0.029
#> Item_4 0.035 0.027 -0.034 -0.054 0.080
#> Item_5 -0.030 0.015 0.028 -0.025 -0.070
#> Item_6 0.036 0.021 0.023 -0.015 0.045
#> Item_7 0.012 0.036 -0.007 0.015 0.024
#> Item_8 -0.046 0.022 0.020 -0.022 0.040
#> Item_9 -0.048 -0.018 -0.014 0.026 0.034
#> Item_10 0.037 0.025 0.052 -0.019 -0.049
#> Item_11 NA 0.010 -0.024 -0.053 0.021
#> Item_12 0.094 NA -0.016 -0.016 0.012
#> Item_13 0.555 0.254 NA -0.013 0.022
#> Item_14 2.862 0.255 0.159 NA 0.009
#> Item_15 0.424 0.148 0.486 0.073 NA
#>
#> $D2
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> Item_1 NA -0.029 0.031 -0.026 0.021 -0.042 -0.006 0.039 0.010 -0.029
#> Item_2 0.861 NA 0.047 -0.060 0.049 -0.061 -0.036 -0.036 0.043 0.035
#> Item_3 0.973 2.251 NA 0.064 0.039 -0.029 0.033 0.045 0.042 0.031
#> Item_4 0.673 3.547 4.082 NA 0.034 0.045 0.029 0.033 -0.031 -0.053
#> Item_5 0.455 2.426 1.534 1.151 NA -0.042 -0.043 -0.030 0.034 -0.026
#> Item_6 1.750 3.773 0.861 2.016 1.752 NA -0.038 0.023 -0.060 0.022
#> Item_7 0.040 1.294 1.085 0.831 1.854 1.475 NA 0.023 -0.021 0.025
#> Item_8 1.530 1.310 1.985 1.122 0.915 0.545 0.539 NA -0.028 -0.026
#> Item_9 0.106 1.832 1.780 0.934 1.137 3.654 0.453 0.760 NA 0.037
#> Item_10 0.815 1.230 0.958 2.779 0.685 0.466 0.622 0.690 1.393 NA
#> Item_11 0.822 0.826 0.800 1.861 0.336 0.218 0.062 2.847 0.285 0.407
#> Item_12 0.087 1.536 1.097 0.639 0.309 0.454 0.096 0.556 0.398 0.520
#> Item_13 0.582 1.458 0.844 1.093 0.620 0.403 0.401 0.619 1.349 0.478
#> Item_14 0.403 1.550 0.914 1.292 0.544 0.798 0.534 3.153 0.137 0.344
#> Item_15 0.338 1.306 1.241 0.980 2.379 1.261 0.615 0.291 0.276 0.325
#> Item_11 Item_12 Item_13 Item_14 Item_15
#> Item_1 0.029 0.009 0.024 0.020 0.018
#> Item_2 0.029 -0.039 0.038 0.039 -0.036
#> Item_3 0.028 0.033 0.029 0.030 0.035
#> Item_4 0.043 -0.025 -0.033 0.036 -0.031
#> Item_5 0.018 -0.018 -0.025 0.023 -0.049
#> Item_6 0.015 -0.021 0.020 -0.028 -0.036
#> Item_7 -0.008 -0.010 -0.020 0.023 -0.025
#> Item_8 0.053 -0.024 -0.025 0.056 0.017
#> Item_9 -0.017 -0.020 -0.037 0.012 -0.017
#> Item_10 0.020 0.023 -0.022 0.019 0.018
#> Item_11 NA 0.032 0.017 0.018 0.024
#> Item_12 1.010 NA 0.014 -0.022 -0.011
#> Item_13 0.280 0.185 NA 0.022 -0.012
#> Item_14 0.333 0.480 0.479 NA -0.007
#> Item_15 0.580 0.131 0.145 0.048 NA
#>
plot(mod_configural)
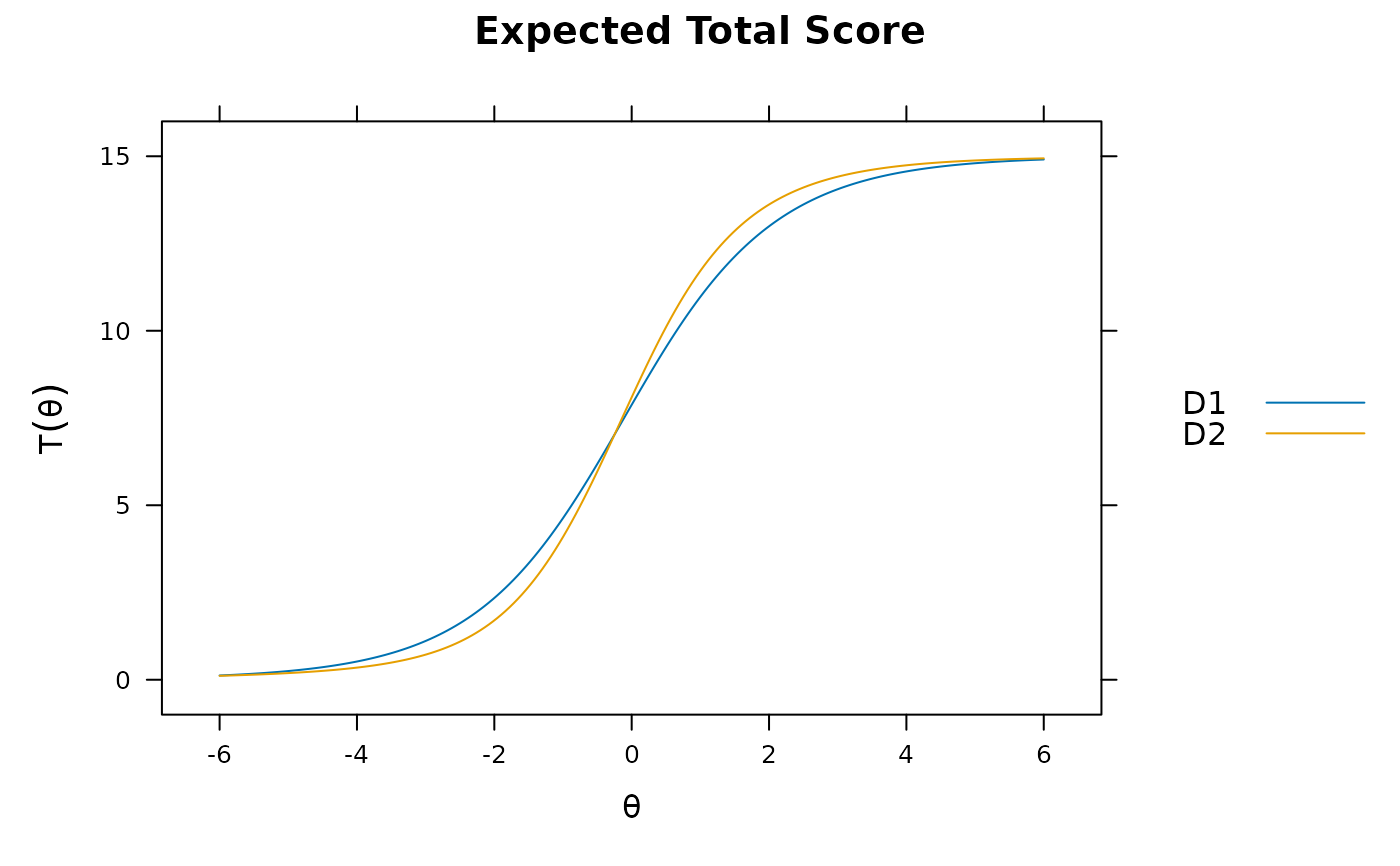plot(mod_configural, type = 'info')
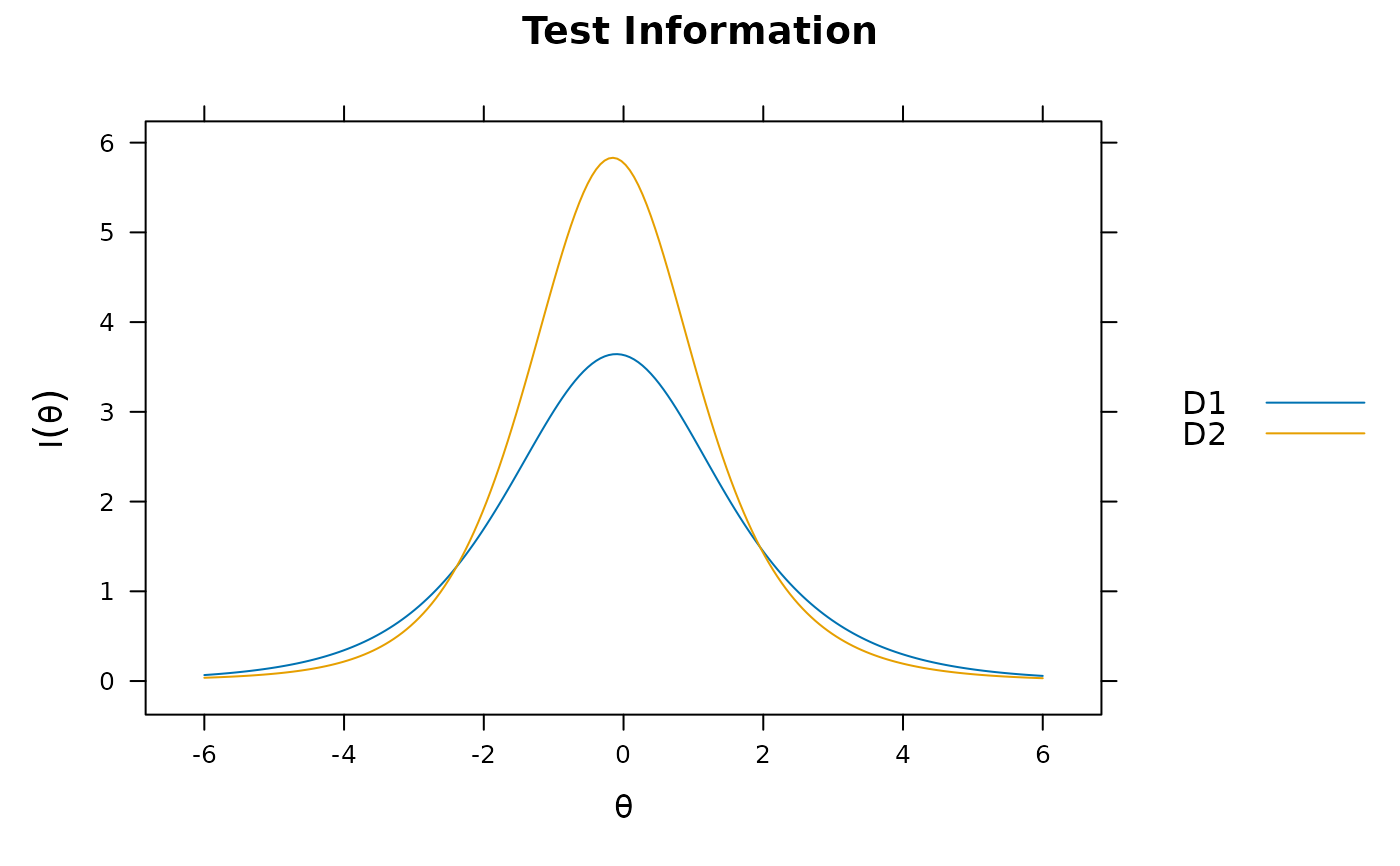plot(mod_configural, type = 'trace')
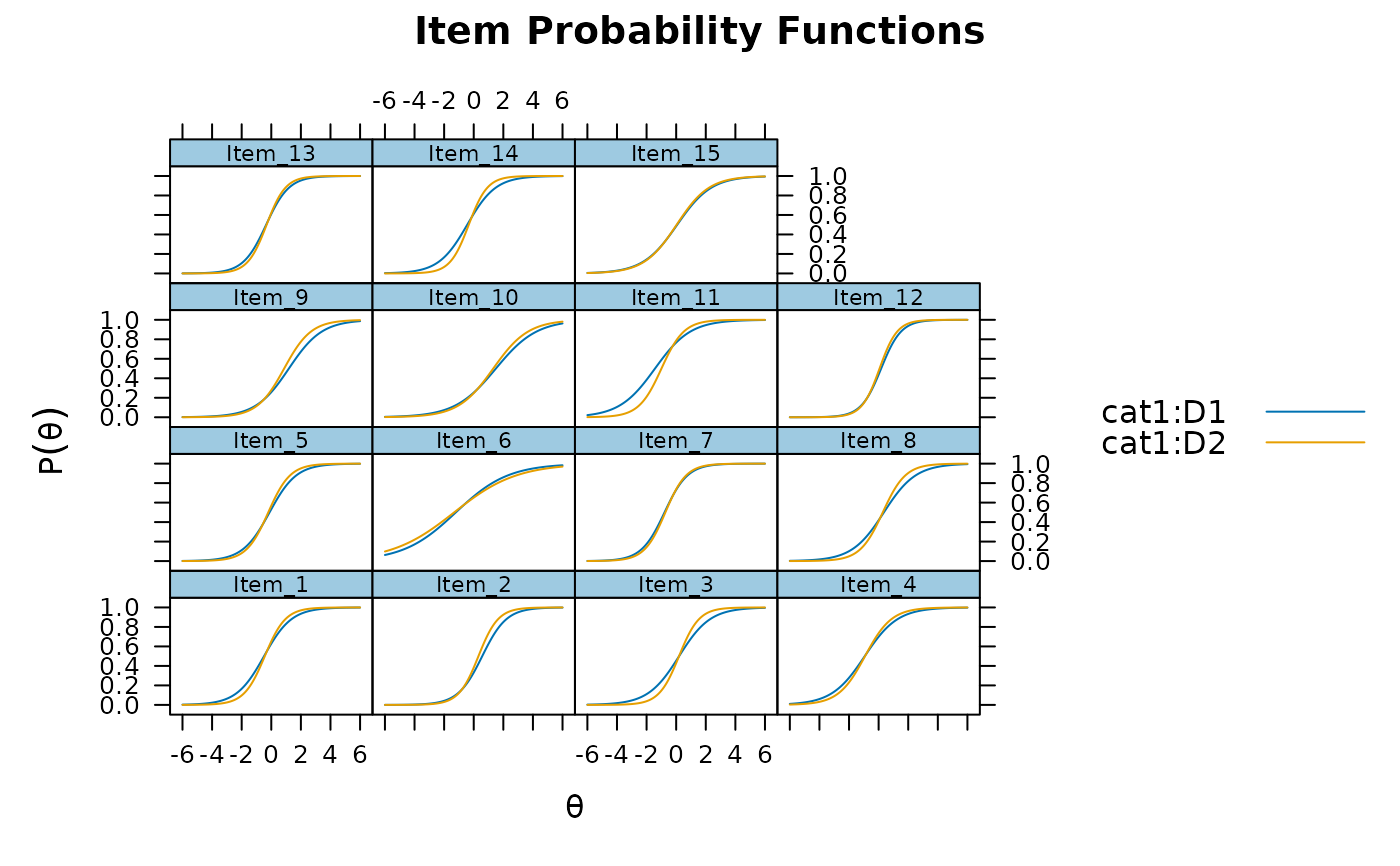plot(mod_configural, type = 'trace', which.items = 1:4)
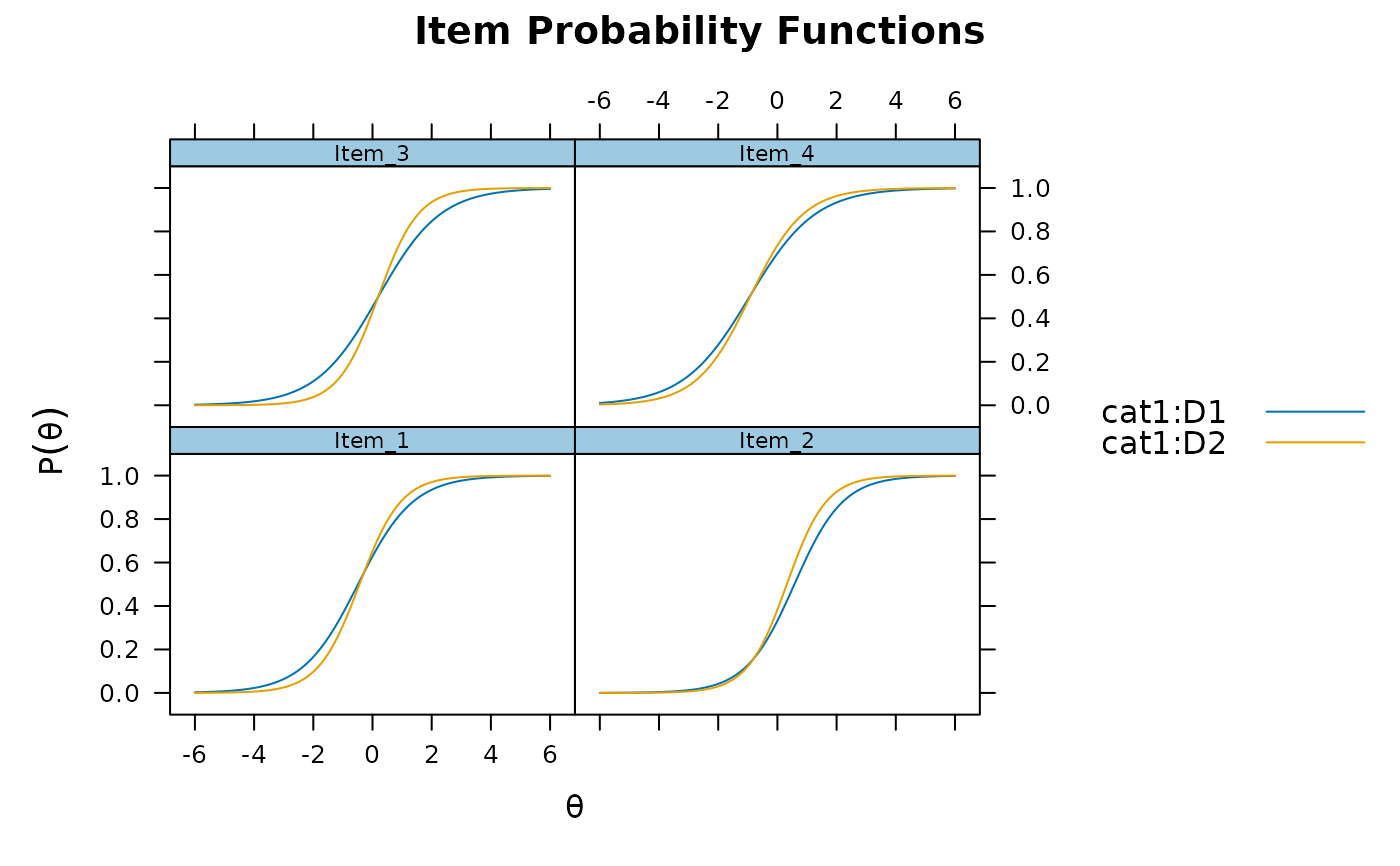itemplot(mod_configural, 2)
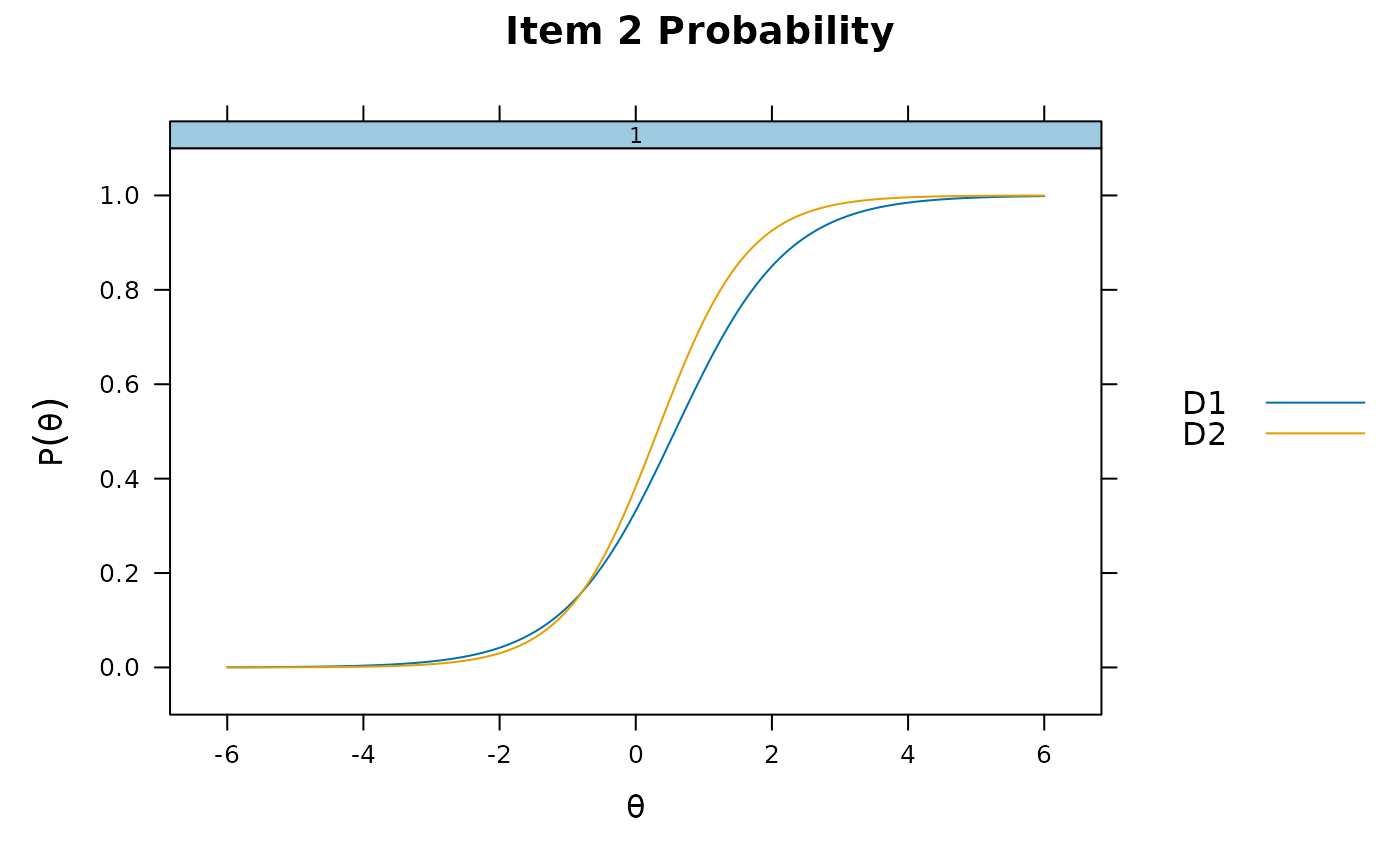itemplot(mod_configural, 2, type = 'RE')
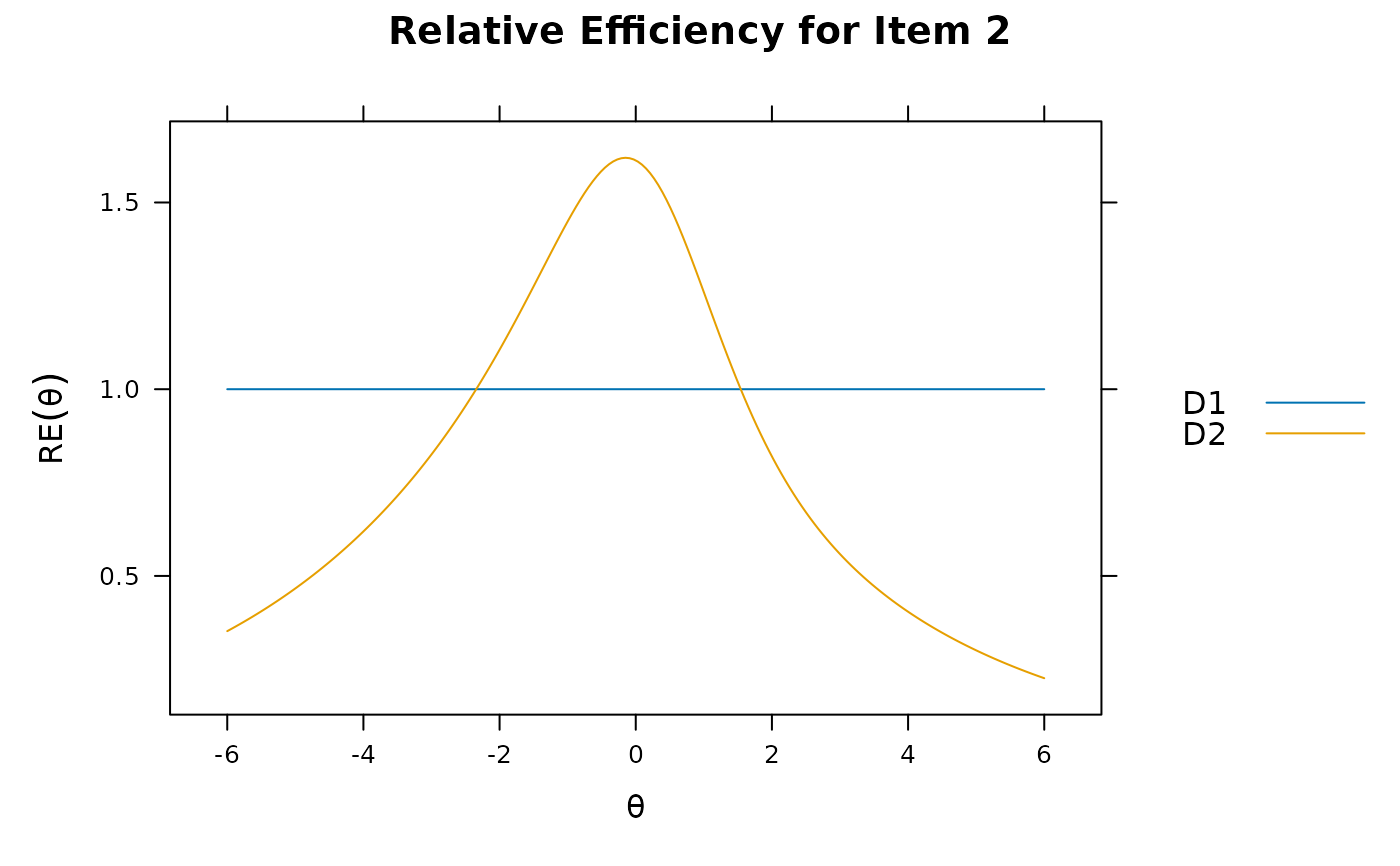anova(mod_metric, mod_configural) #equal slopes only
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_metric 35937.61 36046.68 36030.15 36189.65 -17923.80
#> mod_configural 35927.53 36072.96 36050.92 36263.58 -17903.76 40.08 15 0
anova(mod_scalar2, mod_metric) #equal intercepts, free variance and mean
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_scalar2 35894.66 35972.22 35960.47 36073.89 -17915.33
#> mod_metric 35937.61 36046.68 36030.15 36189.65 -17923.80 -16.947 13 NaN
anova(mod_scalar1, mod_scalar2) #fix mean
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_scalar1 35893.96 35969.10 35957.71 36067.58 -17915.98
#> mod_scalar2 35894.66 35972.22 35960.47 36073.89 -17915.33 1.296 1 0.255
anova(mod_fullconstrain, mod_scalar1) #fix variance
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_fullconstrain 35917.51 35990.22 35979.20 36085.53 -17928.75
#> mod_scalar1 35893.96 35969.10 35957.71 36067.58 -17915.98 25.552 1 0
# compared all at once (in order of most constrained to least)
anova(mod_fullconstrain, mod_scalar2, mod_configural)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_fullconstrain 35917.51 35990.22 35979.20 36085.53 -17928.75
#> mod_scalar2 35894.66 35972.22 35960.47 36073.89 -17915.33 26.848 2 0
#> mod_configural 35927.53 36072.96 36050.92 36263.58 -17903.76 23.133 28 0.726
# test whether first 6 slopes should be equal across groups
values <- multipleGroup(dat, 1, group = group, pars = 'values')
values
#> group item class name parnum value lbound ubound est const
#> 1 D1 Item_1 dich a1 1 0.851 -Inf Inf TRUE none
#> 2 D1 Item_1 dich d 2 0.541 -Inf Inf TRUE none
#> 3 D1 Item_1 dich g 3 0.000 0 1 FALSE none
#> 4 D1 Item_1 dich u 4 1.000 0 1 FALSE none
#> 5 D1 Item_2 dich a1 5 0.851 -Inf Inf TRUE none
#> 6 D1 Item_2 dich d 6 -0.536 -Inf Inf TRUE none
#> 7 D1 Item_2 dich g 7 0.000 0 1 FALSE none
#> 8 D1 Item_2 dich u 8 1.000 0 1 FALSE none
#> 9 D1 Item_3 dich a1 9 0.851 -Inf Inf TRUE none
#> 10 D1 Item_3 dich d 10 -0.220 -Inf Inf TRUE none
#> 11 D1 Item_3 dich g 11 0.000 0 1 FALSE none
#> 12 D1 Item_3 dich u 12 1.000 0 1 FALSE none
#> 13 D1 Item_4 dich a1 13 0.851 -Inf Inf TRUE none
#> 14 D1 Item_4 dich d 14 0.941 -Inf Inf TRUE none
#> 15 D1 Item_4 dich g 15 0.000 0 1 FALSE none
#> 16 D1 Item_4 dich u 16 1.000 0 1 FALSE none
#> 17 D1 Item_5 dich a1 17 0.851 -Inf Inf TRUE none
#> 18 D1 Item_5 dich d 18 0.190 -Inf Inf TRUE none
#> 19 D1 Item_5 dich g 19 0.000 0 1 FALSE none
#> 20 D1 Item_5 dich u 20 1.000 0 1 FALSE none
#> 21 D1 Item_6 dich a1 21 0.851 -Inf Inf TRUE none
#> 22 D1 Item_6 dich d 22 0.752 -Inf Inf TRUE none
#> 23 D1 Item_6 dich g 23 0.000 0 1 FALSE none
#> 24 D1 Item_6 dich u 24 1.000 0 1 FALSE none
#> 25 D1 Item_7 dich a1 25 0.851 -Inf Inf TRUE none
#> 26 D1 Item_7 dich d 26 0.927 -Inf Inf TRUE none
#> 27 D1 Item_7 dich g 27 0.000 0 1 FALSE none
#> 28 D1 Item_7 dich u 28 1.000 0 1 FALSE none
#> 29 D1 Item_8 dich a1 29 0.851 -Inf Inf TRUE none
#> 30 D1 Item_8 dich d 30 -0.339 -Inf Inf TRUE none
#> 31 D1 Item_8 dich g 31 0.000 0 1 FALSE none
#> 32 D1 Item_8 dich u 32 1.000 0 1 FALSE none
#> 33 D1 Item_9 dich a1 33 0.851 -Inf Inf TRUE none
#> 34 D1 Item_9 dich d 34 -1.019 -Inf Inf TRUE none
#> 35 D1 Item_9 dich g 35 0.000 0 1 FALSE none
#> 36 D1 Item_9 dich u 36 1.000 0 1 FALSE none
#> 37 D1 Item_10 dich a1 37 0.851 -Inf Inf TRUE none
#> 38 D1 Item_10 dich d 38 -1.178 -Inf Inf TRUE none
#> 39 D1 Item_10 dich g 39 0.000 0 1 FALSE none
#> 40 D1 Item_10 dich u 40 1.000 0 1 FALSE none
#> 41 D1 Item_11 dich a1 41 0.851 -Inf Inf TRUE none
#> 42 D1 Item_11 dich d 42 1.228 -Inf Inf TRUE none
#> 43 D1 Item_11 dich g 43 0.000 0 1 FALSE none
#> 44 D1 Item_11 dich u 44 1.000 0 1 FALSE none
#> 45 D1 Item_12 dich a1 45 0.851 -Inf Inf TRUE none
#> 46 D1 Item_12 dich d 46 -0.150 -Inf Inf TRUE none
#> 47 D1 Item_12 dich g 47 0.000 0 1 FALSE none
#> 48 D1 Item_12 dich u 48 1.000 0 1 FALSE none
#> 49 D1 Item_13 dich a1 49 0.851 -Inf Inf TRUE none
#> 50 D1 Item_13 dich d 50 0.419 -Inf Inf TRUE none
#> 51 D1 Item_13 dich g 51 0.000 0 1 FALSE none
#> 52 D1 Item_13 dich u 52 1.000 0 1 FALSE none
#> 53 D1 Item_14 dich a1 53 0.851 -Inf Inf TRUE none
#> 54 D1 Item_14 dich d 54 0.455 -Inf Inf TRUE none
#> 55 D1 Item_14 dich g 55 0.000 0 1 FALSE none
#> 56 D1 Item_14 dich u 56 1.000 0 1 FALSE none
#> 57 D1 Item_15 dich a1 57 0.851 -Inf Inf TRUE none
#> 58 D1 Item_15 dich d 58 -0.047 -Inf Inf TRUE none
#> 59 D1 Item_15 dich g 59 0.000 0 1 FALSE none
#> 60 D1 Item_15 dich u 60 1.000 0 1 FALSE none
#> 61 D1 GROUP GroupPars MEAN_1 61 0.000 -Inf Inf FALSE none
#> 62 D1 GROUP GroupPars COV_11 62 1.000 0 Inf FALSE none
#> 63 D2 Item_1 dich a1 63 0.851 -Inf Inf TRUE none
#> 64 D2 Item_1 dich d 64 0.541 -Inf Inf TRUE none
#> 65 D2 Item_1 dich g 65 0.000 0 1 FALSE none
#> 66 D2 Item_1 dich u 66 1.000 0 1 FALSE none
#> 67 D2 Item_2 dich a1 67 0.851 -Inf Inf TRUE none
#> 68 D2 Item_2 dich d 68 -0.536 -Inf Inf TRUE none
#> 69 D2 Item_2 dich g 69 0.000 0 1 FALSE none
#> 70 D2 Item_2 dich u 70 1.000 0 1 FALSE none
#> 71 D2 Item_3 dich a1 71 0.851 -Inf Inf TRUE none
#> 72 D2 Item_3 dich d 72 -0.220 -Inf Inf TRUE none
#> 73 D2 Item_3 dich g 73 0.000 0 1 FALSE none
#> 74 D2 Item_3 dich u 74 1.000 0 1 FALSE none
#> 75 D2 Item_4 dich a1 75 0.851 -Inf Inf TRUE none
#> 76 D2 Item_4 dich d 76 0.941 -Inf Inf TRUE none
#> 77 D2 Item_4 dich g 77 0.000 0 1 FALSE none
#> 78 D2 Item_4 dich u 78 1.000 0 1 FALSE none
#> 79 D2 Item_5 dich a1 79 0.851 -Inf Inf TRUE none
#> 80 D2 Item_5 dich d 80 0.190 -Inf Inf TRUE none
#> 81 D2 Item_5 dich g 81 0.000 0 1 FALSE none
#> 82 D2 Item_5 dich u 82 1.000 0 1 FALSE none
#> 83 D2 Item_6 dich a1 83 0.851 -Inf Inf TRUE none
#> 84 D2 Item_6 dich d 84 0.752 -Inf Inf TRUE none
#> 85 D2 Item_6 dich g 85 0.000 0 1 FALSE none
#> 86 D2 Item_6 dich u 86 1.000 0 1 FALSE none
#> 87 D2 Item_7 dich a1 87 0.851 -Inf Inf TRUE none
#> 88 D2 Item_7 dich d 88 0.927 -Inf Inf TRUE none
#> 89 D2 Item_7 dich g 89 0.000 0 1 FALSE none
#> 90 D2 Item_7 dich u 90 1.000 0 1 FALSE none
#> 91 D2 Item_8 dich a1 91 0.851 -Inf Inf TRUE none
#> 92 D2 Item_8 dich d 92 -0.339 -Inf Inf TRUE none
#> 93 D2 Item_8 dich g 93 0.000 0 1 FALSE none
#> 94 D2 Item_8 dich u 94 1.000 0 1 FALSE none
#> 95 D2 Item_9 dich a1 95 0.851 -Inf Inf TRUE none
#> 96 D2 Item_9 dich d 96 -1.019 -Inf Inf TRUE none
#> 97 D2 Item_9 dich g 97 0.000 0 1 FALSE none
#> 98 D2 Item_9 dich u 98 1.000 0 1 FALSE none
#> 99 D2 Item_10 dich a1 99 0.851 -Inf Inf TRUE none
#> 100 D2 Item_10 dich d 100 -1.178 -Inf Inf TRUE none
#> 101 D2 Item_10 dich g 101 0.000 0 1 FALSE none
#> 102 D2 Item_10 dich u 102 1.000 0 1 FALSE none
#> 103 D2 Item_11 dich a1 103 0.851 -Inf Inf TRUE none
#> 104 D2 Item_11 dich d 104 1.228 -Inf Inf TRUE none
#> 105 D2 Item_11 dich g 105 0.000 0 1 FALSE none
#> 106 D2 Item_11 dich u 106 1.000 0 1 FALSE none
#> 107 D2 Item_12 dich a1 107 0.851 -Inf Inf TRUE none
#> 108 D2 Item_12 dich d 108 -0.150 -Inf Inf TRUE none
#> 109 D2 Item_12 dich g 109 0.000 0 1 FALSE none
#> 110 D2 Item_12 dich u 110 1.000 0 1 FALSE none
#> 111 D2 Item_13 dich a1 111 0.851 -Inf Inf TRUE none
#> 112 D2 Item_13 dich d 112 0.419 -Inf Inf TRUE none
#> 113 D2 Item_13 dich g 113 0.000 0 1 FALSE none
#> 114 D2 Item_13 dich u 114 1.000 0 1 FALSE none
#> 115 D2 Item_14 dich a1 115 0.851 -Inf Inf TRUE none
#> 116 D2 Item_14 dich d 116 0.455 -Inf Inf TRUE none
#> 117 D2 Item_14 dich g 117 0.000 0 1 FALSE none
#> 118 D2 Item_14 dich u 118 1.000 0 1 FALSE none
#> 119 D2 Item_15 dich a1 119 0.851 -Inf Inf TRUE none
#> 120 D2 Item_15 dich d 120 -0.047 -Inf Inf TRUE none
#> 121 D2 Item_15 dich g 121 0.000 0 1 FALSE none
#> 122 D2 Item_15 dich u 122 1.000 0 1 FALSE none
#> 123 D2 GROUP GroupPars MEAN_1 123 0.000 -Inf Inf FALSE none
#> 124 D2 GROUP GroupPars COV_11 124 1.000 0 Inf FALSE none
#> nconst prior.type prior_1 prior_2
#> 1 none none NaN NaN
#> 2 none none NaN NaN
#> 3 none none NaN NaN
#> 4 none none NaN NaN
#> 5 none none NaN NaN
#> 6 none none NaN NaN
#> 7 none none NaN NaN
#> 8 none none NaN NaN
#> 9 none none NaN NaN
#> 10 none none NaN NaN
#> 11 none none NaN NaN
#> 12 none none NaN NaN
#> 13 none none NaN NaN
#> 14 none none NaN NaN
#> 15 none none NaN NaN
#> 16 none none NaN NaN
#> 17 none none NaN NaN
#> 18 none none NaN NaN
#> 19 none none NaN NaN
#> 20 none none NaN NaN
#> 21 none none NaN NaN
#> 22 none none NaN NaN
#> 23 none none NaN NaN
#> 24 none none NaN NaN
#> 25 none none NaN NaN
#> 26 none none NaN NaN
#> 27 none none NaN NaN
#> 28 none none NaN NaN
#> 29 none none NaN NaN
#> 30 none none NaN NaN
#> 31 none none NaN NaN
#> 32 none none NaN NaN
#> 33 none none NaN NaN
#> 34 none none NaN NaN
#> 35 none none NaN NaN
#> 36 none none NaN NaN
#> 37 none none NaN NaN
#> 38 none none NaN NaN
#> 39 none none NaN NaN
#> 40 none none NaN NaN
#> 41 none none NaN NaN
#> 42 none none NaN NaN
#> 43 none none NaN NaN
#> 44 none none NaN NaN
#> 45 none none NaN NaN
#> 46 none none NaN NaN
#> 47 none none NaN NaN
#> 48 none none NaN NaN
#> 49 none none NaN NaN
#> 50 none none NaN NaN
#> 51 none none NaN NaN
#> 52 none none NaN NaN
#> 53 none none NaN NaN
#> 54 none none NaN NaN
#> 55 none none NaN NaN
#> 56 none none NaN NaN
#> 57 none none NaN NaN
#> 58 none none NaN NaN
#> 59 none none NaN NaN
#> 60 none none NaN NaN
#> 61 none none NaN NaN
#> 62 none none NaN NaN
#> 63 none none NaN NaN
#> 64 none none NaN NaN
#> 65 none none NaN NaN
#> 66 none none NaN NaN
#> 67 none none NaN NaN
#> 68 none none NaN NaN
#> 69 none none NaN NaN
#> 70 none none NaN NaN
#> 71 none none NaN NaN
#> 72 none none NaN NaN
#> 73 none none NaN NaN
#> 74 none none NaN NaN
#> 75 none none NaN NaN
#> 76 none none NaN NaN
#> 77 none none NaN NaN
#> 78 none none NaN NaN
#> 79 none none NaN NaN
#> 80 none none NaN NaN
#> 81 none none NaN NaN
#> 82 none none NaN NaN
#> 83 none none NaN NaN
#> 84 none none NaN NaN
#> 85 none none NaN NaN
#> 86 none none NaN NaN
#> 87 none none NaN NaN
#> 88 none none NaN NaN
#> 89 none none NaN NaN
#> 90 none none NaN NaN
#> 91 none none NaN NaN
#> 92 none none NaN NaN
#> 93 none none NaN NaN
#> 94 none none NaN NaN
#> 95 none none NaN NaN
#> 96 none none NaN NaN
#> 97 none none NaN NaN
#> 98 none none NaN NaN
#> 99 none none NaN NaN
#> 100 none none NaN NaN
#> 101 none none NaN NaN
#> 102 none none NaN NaN
#> 103 none none NaN NaN
#> 104 none none NaN NaN
#> 105 none none NaN NaN
#> 106 none none NaN NaN
#> 107 none none NaN NaN
#> 108 none none NaN NaN
#> 109 none none NaN NaN
#> 110 none none NaN NaN
#> 111 none none NaN NaN
#> 112 none none NaN NaN
#> 113 none none NaN NaN
#> 114 none none NaN NaN
#> 115 none none NaN NaN
#> 116 none none NaN NaN
#> 117 none none NaN NaN
#> 118 none none NaN NaN
#> 119 none none NaN NaN
#> 120 none none NaN NaN
#> 121 none none NaN NaN
#> 122 none none NaN NaN
#> 123 none none NaN NaN
#> 124 none none NaN NaN
constrain <- list(c(1, 63), c(5,67), c(9,71), c(13,75), c(17,79), c(21,83))
equalslopes <- multipleGroup(dat, 1, group = group, constrain = constrain)
anova(equalslopes, mod_configural)
#> AIC SABIC HQ BIC logLik X2 df p
#> equalslopes 35935.51 36066.40 36046.56 36237.96 -17913.76
#> mod_configural 35927.53 36072.96 36050.92 36263.58 -17903.76 19.983 6 0.003
# same as above, but using mirt.model syntax
newmodel <- '
F = 1-15
CONSTRAINB = (1-6, a1)'
equalslopes <- multipleGroup(dat, newmodel, group = group)
coef(equalslopes, simplify=TRUE)
#> $D1
#> $items
#> a1 d g u
#> Item_1 1.246 0.546 0 1
#> Item_2 1.356 -0.720 0 1
#> Item_3 1.199 -0.201 0 1
#> Item_4 1.006 0.861 0 1
#> Item_5 1.224 0.131 0 1
#> Item_6 0.515 0.673 0 1
#> Item_7 1.305 0.999 0 1
#> Item_8 0.943 -0.328 0 1
#> Item_9 0.916 -1.058 0 1
#> Item_10 0.731 -1.079 0 1
#> Item_11 0.851 1.186 0 1
#> Item_12 1.515 -0.251 0 1
#> Item_13 1.322 0.444 0 1
#> Item_14 1.058 0.451 0 1
#> Item_15 0.885 -0.061 0 1
#>
#> $means
#> F
#> 0
#>
#> $cov
#> F
#> F 1
#>
#>
#> $D2
#> $items
#> a1 d g u
#> Item_1 1.246 0.599 0 1
#> Item_2 1.356 -0.462 0 1
#> Item_3 1.199 -0.264 0 1
#> Item_4 1.006 1.001 0 1
#> Item_5 1.224 0.266 0 1
#> Item_6 0.515 0.631 0 1
#> Item_7 1.374 1.031 0 1
#> Item_8 1.268 -0.367 0 1
#> Item_9 1.061 -0.952 0 1
#> Item_10 0.826 -1.115 0 1
#> Item_11 1.282 1.308 0 1
#> Item_12 1.625 -0.107 0 1
#> Item_13 1.523 0.493 0 1
#> Item_14 1.545 0.532 0 1
#> Item_15 0.885 -0.030 0 1
#>
#> $means
#> F
#> 0
#>
#> $cov
#> F
#> F 1
#>
#>
############
# vertical scaling (i.e., equating when groups answer items others do not)
dat2 <- dat
dat2[group == 'D1', 1:2] <- dat2[group != 'D1', 14:15] <- NA
head(dat2)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1,] NA NA 1 1 1 0 1 1 0 0
#> [2,] NA NA 1 1 1 1 1 0 1 0
#> [3,] NA NA 0 1 1 1 1 1 0 0
#> [4,] NA NA 1 1 1 1 1 1 0 0
#> [5,] NA NA 1 0 1 1 1 1 1 0
#> [6,] NA NA 1 1 1 1 1 0 0 0
#> Item_11 Item_12 Item_13 Item_14 Item_15
#> [1,] 1 1 0 1 1
#> [2,] 0 1 1 1 1
#> [3,] 1 0 1 1 1
#> [4,] 1 1 1 1 1
#> [5,] 1 1 1 1 1
#> [6,] 1 1 1 1 0
tail(dat2)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1995,] 1 1 0 0 0 1 1 1 0 0
#> [1996,] 1 0 1 1 1 0 1 1 1 1
#> [1997,] 0 1 0 0 0 1 0 1 0 0
#> [1998,] 0 1 0 0 1 0 0 0 0 0
#> [1999,] 1 1 0 1 1 1 1 1 0 0
#> [2000,] 0 0 0 0 0 0 1 0 0 0
#> Item_11 Item_12 Item_13 Item_14 Item_15
#> [1995,] 1 0 1 NA NA
#> [1996,] 1 1 0 NA NA
#> [1997,] 1 0 1 NA NA
#> [1998,] 0 1 0 NA NA
#> [1999,] 1 1 1 NA NA
#> [2000,] 0 0 0 NA NA
# items with missing responses need to be constrained across groups for identification
nms <- colnames(dat2)
mod <- multipleGroup(dat2, 1, group, invariance = nms[c(1:2, 14:15)])
# this will throw an error without proper constraints (SEs cannot be computed either)
# mod <- multipleGroup(dat2, 1, group)
# model still does not have anchors, therefore need to add a few (here use items 3-5)
mod_anchor <- multipleGroup(dat2, 1, group,
invariance = c(nms[c(1:5, 14:15)], 'free_means', 'free_var'))
coef(mod_anchor, simplify=TRUE)
#> $D1
#> $items
#> a1 d g u
#> Item_1 1.108 0.542 0 1
#> Item_2 1.160 -0.564 0 1
#> Item_3 1.073 -0.272 0 1
#> Item_4 0.871 0.895 0 1
#> Item_5 1.089 0.160 0 1
#> Item_6 0.582 0.685 0 1
#> Item_7 1.292 1.009 0 1
#> Item_8 0.906 -0.328 0 1
#> Item_9 0.855 -1.049 0 1
#> Item_10 0.746 -1.089 0 1
#> Item_11 0.866 1.200 0 1
#> Item_12 1.432 -0.247 0 1
#> Item_13 1.244 0.440 0 1
#> Item_14 1.000 0.449 0 1
#> Item_15 0.852 -0.061 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $D2
#> $items
#> a1 d g u
#> Item_1 1.108 0.542 0 1
#> Item_2 1.160 -0.564 0 1
#> Item_3 1.073 -0.272 0 1
#> Item_4 0.871 0.895 0 1
#> Item_5 1.089 0.160 0 1
#> Item_6 0.374 0.596 0 1
#> Item_7 1.090 0.942 0 1
#> Item_8 0.988 -0.437 0 1
#> Item_9 0.854 -1.018 0 1
#> Item_10 0.657 -1.164 0 1
#> Item_11 1.023 1.228 0 1
#> Item_12 1.324 -0.207 0 1
#> Item_13 1.212 0.399 0 1
#> Item_14 1.000 0.449 0 1
#> Item_15 0.852 -0.061 0 1
#>
#> $means
#> F1
#> 0.077
#>
#> $cov
#> F1
#> F1 1.658
#>
#>
# check if identified by computing information matrix
mod_anchor <- multipleGroup(dat2, 1, group, pars = mod2values(mod_anchor), TOL=NaN, SE=TRUE,
invariance = c(nms[c(1:5, 14:15)], 'free_means', 'free_var'))
mod_anchor
#>
#> Call:
#> multipleGroup(data = dat2, model = 1, group = group, invariance = c(nms[c(1:5,
#> 14:15)], "free_means", "free_var"), pars = mod2values(mod_anchor),
#> TOL = NaN, SE = TRUE)
#>
#> Full-information item factor analysis with 1 factor(s).
#> Converged within NaN tolerance after 1 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Number of rectangular quadrature: 61
#> Latent density type: Gaussian
#>
#> Information matrix estimated with method: Oakes
#> Second-order test: model is a possible local maximum
#> Condition number of information matrix = 87.67822
#>
#> Log-likelihood = -15563.53
#> Estimated parameters: 62
#> AIC = 31223.06
#> BIC = 31491.91; SABIC = 31339.41
#>
coef(mod_anchor)
#> $D1
#> $Item_1
#> a1 d g u
#> par 1.108 0.542 0 1
#> CI_2.5 0.842 0.330 NA NA
#> CI_97.5 1.375 0.753 NA NA
#>
#> $Item_2
#> a1 d g u
#> par 1.160 -0.564 0 1
#> CI_2.5 0.883 -0.785 NA NA
#> CI_97.5 1.436 -0.342 NA NA
#>
#> $Item_3
#> a1 d g u
#> par 1.073 -0.272 0 1
#> CI_2.5 0.896 -0.408 NA NA
#> CI_97.5 1.250 -0.137 NA NA
#>
#> $Item_4
#> a1 d g u
#> par 0.871 0.895 0 1
#> CI_2.5 0.710 0.765 NA NA
#> CI_97.5 1.031 1.026 NA NA
#>
#> $Item_5
#> a1 d g u
#> par 1.089 0.160 0 1
#> CI_2.5 0.906 0.024 NA NA
#> CI_97.5 1.272 0.295 NA NA
#>
#> $Item_6
#> a1 d g u
#> par 0.582 0.685 0 1
#> CI_2.5 0.405 0.543 NA NA
#> CI_97.5 0.760 0.828 NA NA
#>
#> $Item_7
#> a1 d g u
#> par 1.292 1.009 0 1
#> CI_2.5 1.027 0.818 NA NA
#> CI_97.5 1.558 1.199 NA NA
#>
#> $Item_8
#> a1 d g u
#> par 0.906 -0.328 0 1
#> CI_2.5 0.702 -0.476 NA NA
#> CI_97.5 1.111 -0.179 NA NA
#>
#> $Item_9
#> a1 d g u
#> par 0.855 -1.049 0 1
#> CI_2.5 0.642 -1.216 NA NA
#> CI_97.5 1.069 -0.882 NA NA
#>
#> $Item_10
#> a1 d g u
#> par 0.746 -1.089 0 1
#> CI_2.5 0.542 -1.253 NA NA
#> CI_97.5 0.950 -0.926 NA NA
#>
#> $Item_11
#> a1 d g u
#> par 0.866 1.200 0 1
#> CI_2.5 0.651 1.025 NA NA
#> CI_97.5 1.081 1.375 NA NA
#>
#> $Item_12
#> a1 d g u
#> par 1.432 -0.247 0 1
#> CI_2.5 1.152 -0.421 NA NA
#> CI_97.5 1.713 -0.074 NA NA
#>
#> $Item_13
#> a1 d g u
#> par 1.244 0.440 0 1
#> CI_2.5 0.994 0.273 NA NA
#> CI_97.5 1.494 0.607 NA NA
#>
#> $Item_14
#> a1 d g u
#> par 1.000 0.449 0 1
#> CI_2.5 0.785 0.294 NA NA
#> CI_97.5 1.215 0.603 NA NA
#>
#> $Item_15
#> a1 d g u
#> par 0.852 -0.061 0 1
#> CI_2.5 0.655 -0.205 NA NA
#> CI_97.5 1.049 0.083 NA NA
#>
#> $GroupPars
#> MEAN_1 COV_11
#> par 0 1
#> CI_2.5 NA NA
#> CI_97.5 NA NA
#>
#>
#> $D2
#> $Item_1
#> a1 d g u
#> par 1.108 0.542 0 1
#> CI_2.5 0.842 0.330 NA NA
#> CI_97.5 1.375 0.753 NA NA
#>
#> $Item_2
#> a1 d g u
#> par 1.160 -0.564 0 1
#> CI_2.5 0.883 -0.785 NA NA
#> CI_97.5 1.436 -0.342 NA NA
#>
#> $Item_3
#> a1 d g u
#> par 1.073 -0.272 0 1
#> CI_2.5 0.896 -0.408 NA NA
#> CI_97.5 1.250 -0.137 NA NA
#>
#> $Item_4
#> a1 d g u
#> par 0.871 0.895 0 1
#> CI_2.5 0.710 0.765 NA NA
#> CI_97.5 1.031 1.026 NA NA
#>
#> $Item_5
#> a1 d g u
#> par 1.089 0.160 0 1
#> CI_2.5 0.906 0.024 NA NA
#> CI_97.5 1.272 0.295 NA NA
#>
#> $Item_6
#> a1 d g u
#> par 0.374 0.596 0 1
#> CI_2.5 0.236 0.454 NA NA
#> CI_97.5 0.512 0.738 NA NA
#>
#> $Item_7
#> a1 d g u
#> par 1.090 0.942 0 1
#> CI_2.5 0.823 0.722 NA NA
#> CI_97.5 1.357 1.163 NA NA
#>
#> $Item_8
#> a1 d g u
#> par 0.988 -0.437 0 1
#> CI_2.5 0.747 -0.636 NA NA
#> CI_97.5 1.228 -0.239 NA NA
#>
#> $Item_9
#> a1 d g u
#> par 0.854 -1.018 0 1
#> CI_2.5 0.635 -1.219 NA NA
#> CI_97.5 1.072 -0.817 NA NA
#>
#> $Item_10
#> a1 d g u
#> par 0.657 -1.164 0 1
#> CI_2.5 0.469 -1.350 NA NA
#> CI_97.5 0.845 -0.978 NA NA
#>
#> $Item_11
#> a1 d g u
#> par 1.023 1.228 0 1
#> CI_2.5 0.766 1.003 NA NA
#> CI_97.5 1.280 1.452 NA NA
#>
#> $Item_12
#> a1 d g u
#> par 1.324 -0.207 0 1
#> CI_2.5 1.010 -0.442 NA NA
#> CI_97.5 1.637 0.027 NA NA
#>
#> $Item_13
#> a1 d g u
#> par 1.212 0.399 0 1
#> CI_2.5 0.923 0.178 NA NA
#> CI_97.5 1.502 0.620 NA NA
#>
#> $Item_14
#> a1 d g u
#> par 1.000 0.449 0 1
#> CI_2.5 0.785 0.294 NA NA
#> CI_97.5 1.215 0.603 NA NA
#>
#> $Item_15
#> a1 d g u
#> par 0.852 -0.061 0 1
#> CI_2.5 0.655 -0.205 NA NA
#> CI_97.5 1.049 0.083 NA NA
#>
#> $GroupPars
#> MEAN_1 COV_11
#> par 0.008 1.658
#> CI_2.5 -0.148 1.093
#> CI_97.5 0.164 2.222
#>
#>
coef(mod_anchor, printSE=TRUE)
#> $D1
#> $Item_1
#> a1 d logit(g) logit(u)
#> par 1.108 0.542 -999 999
#> SE 0.136 0.108 NA NA
#>
#> $Item_2
#> a1 d logit(g) logit(u)
#> par 1.160 -0.564 -999 999
#> SE 0.141 0.113 NA NA
#>
#> $Item_3
#> a1 d logit(g) logit(u)
#> par 1.073 -0.272 -999 999
#> SE 0.090 0.069 NA NA
#>
#> $Item_4
#> a1 d logit(g) logit(u)
#> par 0.871 0.895 -999 999
#> SE 0.082 0.066 NA NA
#>
#> $Item_5
#> a1 d logit(g) logit(u)
#> par 1.089 0.160 -999 999
#> SE 0.093 0.069 NA NA
#>
#> $Item_6
#> a1 d logit(g) logit(u)
#> par 0.582 0.685 -999 999
#> SE 0.091 0.073 NA NA
#>
#> $Item_7
#> a1 d logit(g) logit(u)
#> par 1.292 1.009 -999 999
#> SE 0.135 0.097 NA NA
#>
#> $Item_8
#> a1 d logit(g) logit(u)
#> par 0.906 -0.328 -999 999
#> SE 0.104 0.076 NA NA
#>
#> $Item_9
#> a1 d logit(g) logit(u)
#> par 0.855 -1.049 -999 999
#> SE 0.109 0.085 NA NA
#>
#> $Item_10
#> a1 d logit(g) logit(u)
#> par 0.746 -1.089 -999 999
#> SE 0.104 0.083 NA NA
#>
#> $Item_11
#> a1 d logit(g) logit(u)
#> par 0.866 1.200 -999 999
#> SE 0.110 0.089 NA NA
#>
#> $Item_12
#> a1 d logit(g) logit(u)
#> par 1.432 -0.247 -999 999
#> SE 0.143 0.089 NA NA
#>
#> $Item_13
#> a1 d logit(g) logit(u)
#> par 1.244 0.440 -999 999
#> SE 0.127 0.085 NA NA
#>
#> $Item_14
#> a1 d logit(g) logit(u)
#> par 1.00 0.449 -999 999
#> SE 0.11 0.079 NA NA
#>
#> $Item_15
#> a1 d logit(g) logit(u)
#> par 0.852 -0.061 -999 999
#> SE 0.100 0.073 NA NA
#>
#> $GroupPars
#> MEAN_1 COV_11
#> par 0 1
#> SE NA NA
#>
#>
#> $D2
#> $Item_1
#> a1 d logit(g) logit(u)
#> par 1.108 0.542 -999 999
#> SE 0.136 0.108 NA NA
#>
#> $Item_2
#> a1 d logit(g) logit(u)
#> par 1.160 -0.564 -999 999
#> SE 0.141 0.113 NA NA
#>
#> $Item_3
#> a1 d logit(g) logit(u)
#> par 1.073 -0.272 -999 999
#> SE 0.090 0.069 NA NA
#>
#> $Item_4
#> a1 d logit(g) logit(u)
#> par 0.871 0.895 -999 999
#> SE 0.082 0.066 NA NA
#>
#> $Item_5
#> a1 d logit(g) logit(u)
#> par 1.089 0.160 -999 999
#> SE 0.093 0.069 NA NA
#>
#> $Item_6
#> a1 d logit(g) logit(u)
#> par 0.374 0.596 -999 999
#> SE 0.071 0.073 NA NA
#>
#> $Item_7
#> a1 d logit(g) logit(u)
#> par 1.090 0.942 -999 999
#> SE 0.136 0.112 NA NA
#>
#> $Item_8
#> a1 d logit(g) logit(u)
#> par 0.988 -0.437 -999 999
#> SE 0.123 0.101 NA NA
#>
#> $Item_9
#> a1 d logit(g) logit(u)
#> par 0.854 -1.018 -999 999
#> SE 0.111 0.102 NA NA
#>
#> $Item_10
#> a1 d logit(g) logit(u)
#> par 0.657 -1.164 -999 999
#> SE 0.096 0.095 NA NA
#>
#> $Item_11
#> a1 d logit(g) logit(u)
#> par 1.023 1.228 -999 999
#> SE 0.131 0.114 NA NA
#>
#> $Item_12
#> a1 d logit(g) logit(u)
#> par 1.324 -0.207 -999 999
#> SE 0.160 0.120 NA NA
#>
#> $Item_13
#> a1 d logit(g) logit(u)
#> par 1.212 0.399 -999 999
#> SE 0.148 0.113 NA NA
#>
#> $Item_14
#> a1 d logit(g) logit(u)
#> par 1.00 0.449 -999 999
#> SE 0.11 0.079 NA NA
#>
#> $Item_15
#> a1 d logit(g) logit(u)
#> par 0.852 -0.061 -999 999
#> SE 0.100 0.073 NA NA
#>
#> $GroupPars
#> MEAN_1 COV_11
#> par 0.008 1.658
#> SE 0.080 0.288
#>
#>
#############
# DIF test for each item (using all other items as anchors)
itemnames <- colnames(dat)
refmodel <- multipleGroup(dat, 1, group = group, SE=TRUE,
invariance=c('free_means', 'free_var', itemnames))
# loop over items (in practice, run in parallel to increase speed). May be better to use ?DIF
estmodels <- vector('list', ncol(dat))
for(i in 1:ncol(dat))
estmodels[[i]] <- multipleGroup(dat, 1, group = group, verbose = FALSE,
invariance=c('free_means', 'free_var', itemnames[-i]))
anova(refmodel, estmodels[[1]])
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> estmodels[[1]] 35898.45 35980.86 35968.37 36088.88 -17915.22 0.213 2 0.899
(anovas <- lapply(estmodels, function(x, refmodel) anova(refmodel, x),
refmodel=refmodel))
#> [[1]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35898.45 35980.86 35968.37 36088.88 -17915.22 0.213 2 0.899
#>
#> [[2]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.81 35979.22 35966.73 36087.24 -17914.41 1.847 2 0.397
#>
#> [[3]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35893.66 35976.07 35963.58 36084.09 -17912.83 5.001 2 0.082
#>
#> [[4]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.07 35979.48 35967.00 36087.50 -17914.54 1.586 2 0.453
#>
#> [[5]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.97 35980.38 35967.89 36088.40 -17914.99 0.688 2 0.709
#>
#> [[6]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35894.87 35977.28 35964.79 36085.30 -17913.43 3.793 2 0.15
#>
#> [[7]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.53 35979.94 35967.45 36087.96 -17914.76 1.131 2 0.568
#>
#> [[8]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.20 35979.61 35967.12 36087.63 -17914.60 1.462 2 0.481
#>
#> [[9]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35898.46 35980.87 35968.38 36088.89 -17915.23 0.197 2 0.906
#>
#> [[10]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.67 35980.08 35967.59 36088.10 -17914.83 0.993 2 0.609
#>
#> [[11]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.07 35978.48 35965.99 36086.50 -17914.03 2.593 2 0.273
#>
#> [[12]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35897.57 35979.98 35967.49 36088.00 -17914.78 1.092 2 0.579
#>
#> [[13]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35898.47 35980.88 35968.39 36088.90 -17915.23 0.192 2 0.908
#>
#> [[14]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.15 35978.57 35966.08 36086.58 -17914.08 2.505 2 0.286
#>
#> [[15]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.96 35979.37 35966.88 36087.39 -17914.48 1.699 2 0.428
#>
# family-wise error control
p <- do.call(rbind, lapply(anovas, function(x) x[2, 'p']))
p.adjust(p, method = 'BH')
#> [1] 0.9084068 0.8299977 0.8299977 0.8299977 0.8862361 0.8299977 0.8299977
#> [8] 0.8299977 0.9084068 0.8299977 0.8299977 0.8299977 0.9084068 0.8299977
#> [15] 0.8299977
# same as above, except only test if slopes vary (1 df)
# constrain all intercepts
estmodels <- vector('list', ncol(dat))
for(i in 1:ncol(dat))
estmodels[[i]] <- multipleGroup(dat, 1, group = group, verbose = FALSE,
invariance=c('free_means', 'free_var', 'intercepts',
itemnames[-i]))
(anovas <- lapply(estmodels, function(x, refmodel) anova(refmodel, x),
refmodel=refmodel))
#> [[1]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.52 35976.50 35964.38 36081.35 -17915.26 0.143 1 0.705
#>
#> [[2]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.60 35976.58 35964.46 36081.43 -17915.30 0.061 1 0.804
#>
#> [[3]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35894.66 35974.65 35962.53 36079.49 -17914.33 1.997 1 0.158
#>
#> [[4]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.39 35976.38 35964.26 36081.22 -17915.20 0.268 1 0.605
#>
#> [[5]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.56 35976.54 35964.42 36081.39 -17915.28 0.103 1 0.748
#>
#> [[6]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35893.62 35973.60 35961.48 36078.45 -17913.81 3.042 1 0.081
#>
#> [[7]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35895.67 35975.66 35963.54 36080.50 -17914.84 0.985 1 0.321
#>
#> [[8]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.27 35976.26 35964.13 36081.10 -17915.13 0.39 1 0.532
#>
#> [[9]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.66 35976.64 35964.52 36081.49 -17915.33 0.001 1 0.979
#>
#> [[10]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.12 35976.11 35963.99 36080.95 -17915.06 0.538 1 0.463
#>
#> [[11]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35894.22 35974.21 35962.08 36079.05 -17914.11 2.44 1 0.118
#>
#> [[12]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35895.87 35975.86 35963.74 36080.70 -17914.94 0.79 1 0.374
#>
#> [[13]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35896.58 35976.57 35964.44 36081.41 -17915.29 0.08 1 0.778
#>
#> [[14]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35894.16 35974.15 35962.02 36078.99 -17914.08 2.5 1 0.114
#>
#> [[15]]
#> AIC SABIC HQ BIC logLik X2 df p
#> refmodel 35894.66 35972.22 35960.47 36073.89 -17915.33
#> x 35894.99 35974.97 35962.85 36079.82 -17914.49 1.672 1 0.196
#>
# quickly test with Wald test using DIF()
mod_configural2 <- multipleGroup(dat, 1, group = group, SE=TRUE)
DIF(mod_configural2, which.par = c('a1', 'd'), Wald=TRUE, p.adjust = 'fdr')
#> NOTE: No hyper-parameters were estimated in the DIF model.
#> For effective DIF testing, freeing the focal group hyper-parameters is recommended.
#> groups W df p adj_p
#> Item_1 D1,D2 4.636 2 0.098 0.246
#> Item_2 D1,D2 7.265 2 0.026 0.099
#> Item_3 D1,D2 10.375 2 0.006 0.055
#> Item_4 D1,D2 3.210 2 0.201 0.335
#> Item_5 D1,D2 3.618 2 0.164 0.307
#> Item_6 D1,D2 0.820 2 0.664 0.804
#> Item_7 D1,D2 0.575 2 0.75 0.804
#> Item_8 D1,D2 5.782 2 0.056 0.167
#> Item_9 D1,D2 3.802 2 0.149 0.307
#> Item_10 D1,D2 0.722 2 0.697 0.804
#> Item_11 D1,D2 8.922 2 0.012 0.058
#> Item_12 D1,D2 2.340 2 0.31 0.463
#> Item_13 D1,D2 2.162 2 0.339 0.463
#> Item_14 D1,D2 9.848 2 0.007 0.055
#> Item_15 D1,D2 0.204 2 0.903 0.903
#############
# Three group model where the latent variable parameters are constrained to
# be equal in the focal groups
set.seed(12345)
a <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d <- matrix(rnorm(15,0,.7),ncol=1)
itemtype <- rep('2PL', nrow(a))
N <- 1000
dataset1 <- simdata(a, d, N, itemtype)
dataset2 <- simdata(a, d, N, itemtype, mu = .1, sigma = matrix(1.5))
dataset3 <- simdata(a, d, N, itemtype, mu = .1, sigma = matrix(1.5))
dat <- rbind(dataset1, dataset2, dataset3)
group <- rep(c('D1', 'D2', 'D3'), each=N)
# marginal information
itemstats(dat)
#> $overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 3000 7.89 3.567 0.19 0.054 0.779 1.676
#>
#> $itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 3000 0.605 0.489 0.525 0.415 0.764
#> Item_2 3000 0.403 0.491 0.563 0.458 0.761
#> Item_3 3000 0.457 0.498 0.504 0.388 0.767
#> Item_4 3000 0.676 0.468 0.458 0.345 0.770
#> Item_5 3000 0.545 0.498 0.539 0.429 0.763
#> Item_6 3000 0.645 0.478 0.334 0.207 0.782
#> Item_7 3000 0.688 0.464 0.529 0.426 0.764
#> Item_8 3000 0.427 0.495 0.498 0.382 0.767
#> Item_9 3000 0.292 0.455 0.454 0.344 0.770
#> Item_10 3000 0.284 0.451 0.393 0.279 0.775
#> Item_11 3000 0.738 0.440 0.451 0.345 0.770
#> Item_12 3000 0.460 0.499 0.598 0.496 0.757
#> Item_13 3000 0.591 0.492 0.556 0.449 0.761
#> Item_14 3000 0.591 0.492 0.548 0.441 0.762
#> Item_15 3000 0.488 0.500 0.452 0.330 0.772
#>
#> $proportions
#> 0 1
#> Item_1 0.395 0.605
#> Item_2 0.597 0.403
#> Item_3 0.543 0.457
#> Item_4 0.324 0.676
#> Item_5 0.455 0.545
#> Item_6 0.355 0.645
#> Item_7 0.312 0.688
#> Item_8 0.573 0.427
#> Item_9 0.708 0.292
#> Item_10 0.716 0.284
#> Item_11 0.262 0.738
#> Item_12 0.540 0.460
#> Item_13 0.409 0.591
#> Item_14 0.409 0.591
#> Item_15 0.512 0.488
#>
# conditional information
itemstats(dat, group=group)
#> $D1
#> $D1$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 1000 7.82 3.346 0.159 0.047 0.74 1.705
#>
#> $D1$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 1000 0.605 0.489 0.484 0.361 0.725
#> Item_2 1000 0.368 0.483 0.507 0.388 0.722
#> Item_3 1000 0.461 0.499 0.471 0.343 0.727
#> Item_4 1000 0.673 0.469 0.439 0.315 0.729
#> Item_5 1000 0.526 0.500 0.500 0.376 0.723
#> Item_6 1000 0.654 0.476 0.355 0.222 0.739
#> Item_7 1000 0.683 0.466 0.508 0.394 0.722
#> Item_8 1000 0.431 0.495 0.462 0.333 0.728
#> Item_9 1000 0.287 0.453 0.419 0.298 0.731
#> Item_10 1000 0.274 0.446 0.372 0.249 0.735
#> Item_11 1000 0.739 0.439 0.401 0.282 0.732
#> Item_12 1000 0.456 0.498 0.563 0.448 0.715
#> Item_13 1000 0.584 0.493 0.535 0.416 0.719
#> Item_14 1000 0.592 0.492 0.483 0.358 0.725
#> Item_15 1000 0.487 0.500 0.451 0.321 0.729
#>
#> $D1$proportions
#> 0 1
#> Item_1 0.395 0.605
#> Item_2 0.632 0.368
#> Item_3 0.539 0.461
#> Item_4 0.327 0.673
#> Item_5 0.474 0.526
#> Item_6 0.346 0.654
#> Item_7 0.317 0.683
#> Item_8 0.569 0.431
#> Item_9 0.713 0.287
#> Item_10 0.726 0.274
#> Item_11 0.261 0.739
#> Item_12 0.544 0.456
#> Item_13 0.416 0.584
#> Item_14 0.408 0.592
#> Item_15 0.513 0.487
#>
#>
#> $D2
#> $D2$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 1000 7.955 3.754 0.217 0.065 0.807 1.65
#>
#> $D2$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 1000 0.612 0.488 0.563 0.464 0.792
#> Item_2 1000 0.417 0.493 0.569 0.469 0.792
#> Item_3 1000 0.450 0.498 0.578 0.479 0.791
#> Item_4 1000 0.695 0.461 0.484 0.381 0.798
#> Item_5 1000 0.551 0.498 0.553 0.451 0.793
#> Item_6 1000 0.644 0.479 0.316 0.195 0.811
#> Item_7 1000 0.680 0.467 0.540 0.443 0.794
#> Item_8 1000 0.432 0.496 0.544 0.440 0.794
#> Item_9 1000 0.317 0.466 0.470 0.365 0.799
#> Item_10 1000 0.275 0.447 0.403 0.297 0.804
#> Item_11 1000 0.729 0.445 0.508 0.413 0.796
#> Item_12 1000 0.483 0.500 0.606 0.511 0.788
#> Item_13 1000 0.585 0.493 0.587 0.491 0.790
#> Item_14 1000 0.591 0.492 0.589 0.493 0.790
#> Item_15 1000 0.494 0.500 0.466 0.351 0.801
#>
#> $D2$proportions
#> 0 1
#> Item_1 0.388 0.612
#> Item_2 0.583 0.417
#> Item_3 0.550 0.450
#> Item_4 0.305 0.695
#> Item_5 0.449 0.551
#> Item_6 0.356 0.644
#> Item_7 0.320 0.680
#> Item_8 0.568 0.432
#> Item_9 0.683 0.317
#> Item_10 0.725 0.275
#> Item_11 0.271 0.729
#> Item_12 0.517 0.483
#> Item_13 0.415 0.585
#> Item_14 0.409 0.591
#> Item_15 0.506 0.494
#>
#>
#> $D3
#> $D3$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 1000 7.894 3.592 0.194 0.064 0.783 1.672
#>
#> $D3$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 1000 0.599 0.490 0.526 0.416 0.769
#> Item_2 1000 0.424 0.494 0.610 0.512 0.761
#> Item_3 1000 0.459 0.499 0.460 0.340 0.776
#> Item_4 1000 0.659 0.474 0.452 0.338 0.775
#> Item_5 1000 0.557 0.497 0.562 0.456 0.766
#> Item_6 1000 0.638 0.481 0.334 0.208 0.786
#> Item_7 1000 0.700 0.458 0.539 0.439 0.767
#> Item_8 1000 0.419 0.494 0.485 0.369 0.773
#> Item_9 1000 0.272 0.445 0.470 0.365 0.773
#> Item_10 1000 0.303 0.460 0.405 0.290 0.779
#> Item_11 1000 0.747 0.435 0.438 0.333 0.776
#> Item_12 1000 0.442 0.497 0.622 0.526 0.759
#> Item_13 1000 0.604 0.489 0.545 0.438 0.767
#> Item_14 1000 0.589 0.492 0.569 0.465 0.765
#> Item_15 1000 0.482 0.500 0.439 0.317 0.778
#>
#> $D3$proportions
#> 0 1
#> Item_1 0.401 0.599
#> Item_2 0.576 0.424
#> Item_3 0.541 0.459
#> Item_4 0.341 0.659
#> Item_5 0.443 0.557
#> Item_6 0.362 0.638
#> Item_7 0.300 0.700
#> Item_8 0.581 0.419
#> Item_9 0.728 0.272
#> Item_10 0.697 0.303
#> Item_11 0.253 0.747
#> Item_12 0.558 0.442
#> Item_13 0.396 0.604
#> Item_14 0.411 0.589
#> Item_15 0.518 0.482
#>
#>
model <- 'F1 = 1-15
FREE[D2, D3] = (GROUP, MEAN_1), (GROUP, COV_11)
CONSTRAINB[D2,D3] = (GROUP, MEAN_1), (GROUP, COV_11)'
mod <- multipleGroup(dat, model, group = group, invariance = colnames(dat))
coef(mod, simplify=TRUE)
#> $D1
#> $items
#> a1 d g u
#> Item_1 1.089 0.517 0 1
#> Item_2 1.302 -0.601 0 1
#> Item_3 0.950 -0.251 0 1
#> Item_4 0.857 0.847 0 1
#> Item_5 1.119 0.195 0 1
#> Item_6 0.447 0.618 0 1
#> Item_7 1.209 1.023 0 1
#> Item_8 0.939 -0.396 0 1
#> Item_9 0.909 -1.110 0 1
#> Item_10 0.695 -1.073 0 1
#> Item_11 0.929 1.232 0 1
#> Item_12 1.454 -0.290 0 1
#> Item_13 1.216 0.457 0 1
#> Item_14 1.199 0.453 0 1
#> Item_15 0.751 -0.085 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $D2
#> $items
#> a1 d g u
#> Item_1 1.089 0.517 0 1
#> Item_2 1.302 -0.601 0 1
#> Item_3 0.950 -0.251 0 1
#> Item_4 0.857 0.847 0 1
#> Item_5 1.119 0.195 0 1
#> Item_6 0.447 0.618 0 1
#> Item_7 1.209 1.023 0 1
#> Item_8 0.939 -0.396 0 1
#> Item_9 0.909 -1.110 0 1
#> Item_10 0.695 -1.073 0 1
#> Item_11 0.929 1.232 0 1
#> Item_12 1.454 -0.290 0 1
#> Item_13 1.216 0.457 0 1
#> Item_14 1.199 0.453 0 1
#> Item_15 0.751 -0.085 0 1
#>
#> $means
#> F1
#> 0.055
#>
#> $cov
#> F1
#> F1 1.467
#>
#>
#> $D3
#> $items
#> a1 d g u
#> Item_1 1.089 0.517 0 1
#> Item_2 1.302 -0.601 0 1
#> Item_3 0.950 -0.251 0 1
#> Item_4 0.857 0.847 0 1
#> Item_5 1.119 0.195 0 1
#> Item_6 0.447 0.618 0 1
#> Item_7 1.209 1.023 0 1
#> Item_8 0.939 -0.396 0 1
#> Item_9 0.909 -1.110 0 1
#> Item_10 0.695 -1.073 0 1
#> Item_11 0.929 1.232 0 1
#> Item_12 1.454 -0.290 0 1
#> Item_13 1.216 0.457 0 1
#> Item_14 1.199 0.453 0 1
#> Item_15 0.751 -0.085 0 1
#>
#> $means
#> F1
#> 0.055
#>
#> $cov
#> F1
#> F1 1.467
#>
#>
#############
# Testing main effects in multiple independent grouping variables
set.seed(1234)
a <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d <- matrix(rnorm(15,0,.7),ncol=1)
itemtype <- rep('2PL', nrow(a))
N <- 500
# generated data have interaction effect for latent means, as well as a
# main effect across D but no main effect across G
d11 <- simdata(a, d, N, itemtype, mu = 0)
d12 <- simdata(a, d, N, itemtype, mu = 0)
d13 <- simdata(a, d, N, itemtype, mu = 0)
d21 <- simdata(a, d, N, itemtype, mu = 1/2)
d22 <- simdata(a, d, N, itemtype, mu = 1/2)
d23 <- simdata(a, d, N, itemtype, mu = -1)
dat <- do.call(rbind, list(d11, d12, d13, d21, d22, d23))
group <- rep(c('G1.D1', 'G1.D2', 'G1.D3', 'G2.D1', 'G2.D2', 'G2.D3'), each=N)
table(group)
#> group
#> G1.D1 G1.D2 G1.D3 G2.D1 G2.D2 G2.D3
#> 500 500 500 500 500 500
# in practice, group would be organized in a data.frame as follows
df <- data.frame(group)
dfw <- tidyr::separate_wider_delim(df, group, delim='.', names = c('G', 'D'))
head(dfw)
#> # A tibble: 6 × 2
#> G D
#> <chr> <chr>
#> 1 G1 D1
#> 2 G1 D1
#> 3 G1 D1
#> 4 G1 D1
#> 5 G1 D1
#> 6 G1 D1
# for use with multipleGroup() combine into a single long group
group <- with(dfw, factor(G):factor(D))
# conditional information
itemstats(dat, group=group)
#> $`G1:D1`
#> $`G1:D1`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 6.974 3.126 0.126 0.071 0.685 1.753
#>
#> $`G1:D1`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.456 0.499 0.418 0.273 0.673
#> Item_2 500 0.414 0.493 0.554 0.430 0.652
#> Item_3 500 0.398 0.490 0.543 0.418 0.654
#> Item_4 500 0.382 0.486 0.221 0.067 0.698
#> Item_5 500 0.806 0.396 0.360 0.243 0.676
#> Item_6 500 0.520 0.500 0.532 0.402 0.656
#> Item_7 500 0.452 0.498 0.454 0.314 0.667
#> Item_8 500 0.436 0.496 0.458 0.319 0.667
#> Item_9 500 0.600 0.490 0.379 0.233 0.678
#> Item_10 500 0.408 0.492 0.385 0.239 0.677
#> Item_11 500 0.324 0.468 0.472 0.344 0.664
#> Item_12 500 0.572 0.495 0.310 0.157 0.688
#> Item_13 500 0.334 0.472 0.347 0.204 0.681
#> Item_14 500 0.514 0.500 0.536 0.407 0.655
#> Item_15 500 0.358 0.480 0.472 0.340 0.664
#>
#> $`G1:D1`$proportions
#> 0 1
#> Item_1 0.544 0.456
#> Item_2 0.586 0.414
#> Item_3 0.602 0.398
#> Item_4 0.618 0.382
#> Item_5 0.194 0.806
#> Item_6 0.480 0.520
#> Item_7 0.548 0.452
#> Item_8 0.564 0.436
#> Item_9 0.400 0.600
#> Item_10 0.592 0.408
#> Item_11 0.676 0.324
#> Item_12 0.428 0.572
#> Item_13 0.666 0.334
#> Item_14 0.486 0.514
#> Item_15 0.642 0.358
#>
#>
#> $`G1:D2`
#> $`G1:D2`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 6.768 3.144 0.133 0.062 0.695 1.736
#>
#> $`G1:D2`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.468 0.499 0.410 0.265 0.685
#> Item_2 500 0.440 0.497 0.502 0.369 0.671
#> Item_3 500 0.366 0.482 0.552 0.431 0.664
#> Item_4 500 0.364 0.482 0.294 0.146 0.699
#> Item_5 500 0.800 0.400 0.437 0.326 0.678
#> Item_6 500 0.506 0.500 0.485 0.349 0.674
#> Item_7 500 0.424 0.495 0.440 0.300 0.680
#> Item_8 500 0.422 0.494 0.449 0.310 0.679
#> Item_9 500 0.584 0.493 0.376 0.230 0.689
#> Item_10 500 0.396 0.490 0.315 0.166 0.697
#> Item_11 500 0.242 0.429 0.451 0.332 0.677
#> Item_12 500 0.588 0.493 0.403 0.259 0.685
#> Item_13 500 0.326 0.469 0.360 0.220 0.690
#> Item_14 500 0.480 0.500 0.507 0.374 0.671
#> Item_15 500 0.362 0.481 0.566 0.448 0.662
#>
#> $`G1:D2`$proportions
#> 0 1
#> Item_1 0.532 0.468
#> Item_2 0.560 0.440
#> Item_3 0.634 0.366
#> Item_4 0.636 0.364
#> Item_5 0.200 0.800
#> Item_6 0.494 0.506
#> Item_7 0.576 0.424
#> Item_8 0.578 0.422
#> Item_9 0.416 0.584
#> Item_10 0.604 0.396
#> Item_11 0.758 0.242
#> Item_12 0.412 0.588
#> Item_13 0.674 0.326
#> Item_14 0.520 0.480
#> Item_15 0.638 0.362
#>
#>
#> $`G1:D3`
#> $`G1:D3`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 7.082 3.101 0.124 0.048 0.68 1.755
#>
#> $`G1:D3`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.458 0.499 0.385 0.236 0.671
#> Item_2 500 0.428 0.495 0.513 0.381 0.652
#> Item_3 500 0.426 0.495 0.511 0.379 0.652
#> Item_4 500 0.356 0.479 0.331 0.184 0.678
#> Item_5 500 0.798 0.402 0.433 0.319 0.662
#> Item_6 500 0.560 0.497 0.464 0.325 0.659
#> Item_7 500 0.458 0.499 0.394 0.246 0.670
#> Item_8 500 0.446 0.498 0.406 0.260 0.668
#> Item_9 500 0.582 0.494 0.411 0.266 0.667
#> Item_10 500 0.398 0.490 0.399 0.254 0.669
#> Item_11 500 0.292 0.455 0.399 0.265 0.667
#> Item_12 500 0.620 0.486 0.408 0.265 0.667
#> Item_13 500 0.346 0.476 0.388 0.246 0.670
#> Item_14 500 0.518 0.500 0.480 0.342 0.657
#> Item_15 500 0.396 0.490 0.484 0.349 0.656
#>
#> $`G1:D3`$proportions
#> 0 1
#> Item_1 0.542 0.458
#> Item_2 0.572 0.428
#> Item_3 0.574 0.426
#> Item_4 0.644 0.356
#> Item_5 0.202 0.798
#> Item_6 0.440 0.560
#> Item_7 0.542 0.458
#> Item_8 0.554 0.446
#> Item_9 0.418 0.582
#> Item_10 0.602 0.398
#> Item_11 0.708 0.292
#> Item_12 0.380 0.620
#> Item_13 0.654 0.346
#> Item_14 0.482 0.518
#> Item_15 0.604 0.396
#>
#>
#> $`G2:D1`
#> $`G2:D1`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 8.256 3.22 0.141 0.062 0.711 1.731
#>
#> $`G2:D1`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.582 0.494 0.435 0.299 0.699
#> Item_2 500 0.504 0.500 0.502 0.372 0.690
#> Item_3 500 0.482 0.500 0.518 0.390 0.688
#> Item_4 500 0.410 0.492 0.223 0.072 0.724
#> Item_5 500 0.872 0.334 0.390 0.296 0.700
#> Item_6 500 0.620 0.486 0.514 0.390 0.688
#> Item_7 500 0.490 0.500 0.439 0.301 0.698
#> Item_8 500 0.518 0.500 0.491 0.360 0.691
#> Item_9 500 0.652 0.477 0.435 0.304 0.698
#> Item_10 500 0.500 0.501 0.472 0.338 0.694
#> Item_11 500 0.348 0.477 0.408 0.274 0.701
#> Item_12 500 0.670 0.471 0.442 0.313 0.697
#> Item_13 500 0.442 0.497 0.439 0.302 0.698
#> Item_14 500 0.652 0.477 0.459 0.330 0.695
#> Item_15 500 0.514 0.500 0.513 0.384 0.688
#>
#> $`G2:D1`$proportions
#> 0 1
#> Item_1 0.418 0.582
#> Item_2 0.496 0.504
#> Item_3 0.518 0.482
#> Item_4 0.590 0.410
#> Item_5 0.128 0.872
#> Item_6 0.380 0.620
#> Item_7 0.510 0.490
#> Item_8 0.482 0.518
#> Item_9 0.348 0.652
#> Item_10 0.500 0.500
#> Item_11 0.652 0.348
#> Item_12 0.330 0.670
#> Item_13 0.558 0.442
#> Item_14 0.348 0.652
#> Item_15 0.486 0.514
#>
#>
#> $`G2:D2`
#> $`G2:D2`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 8.268 3.157 0.131 0.064 0.693 1.75
#>
#> $`G2:D2`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.576 0.495 0.303 0.151 0.696
#> Item_2 500 0.538 0.499 0.499 0.366 0.669
#> Item_3 500 0.516 0.500 0.533 0.405 0.664
#> Item_4 500 0.392 0.489 0.271 0.120 0.699
#> Item_5 500 0.836 0.371 0.438 0.336 0.675
#> Item_6 500 0.618 0.486 0.529 0.404 0.664
#> Item_7 500 0.518 0.500 0.458 0.319 0.675
#> Item_8 500 0.548 0.498 0.401 0.256 0.683
#> Item_9 500 0.646 0.479 0.373 0.232 0.686
#> Item_10 500 0.476 0.500 0.438 0.297 0.678
#> Item_11 500 0.392 0.489 0.396 0.254 0.683
#> Item_12 500 0.682 0.466 0.431 0.300 0.677
#> Item_13 500 0.434 0.496 0.448 0.309 0.676
#> Item_14 500 0.616 0.487 0.462 0.328 0.674
#> Item_15 500 0.480 0.500 0.543 0.416 0.662
#>
#> $`G2:D2`$proportions
#> 0 1
#> Item_1 0.424 0.576
#> Item_2 0.462 0.538
#> Item_3 0.484 0.516
#> Item_4 0.608 0.392
#> Item_5 0.164 0.836
#> Item_6 0.382 0.618
#> Item_7 0.482 0.518
#> Item_8 0.452 0.548
#> Item_9 0.354 0.646
#> Item_10 0.524 0.476
#> Item_11 0.608 0.392
#> Item_12 0.318 0.682
#> Item_13 0.566 0.434
#> Item_14 0.384 0.616
#> Item_15 0.520 0.480
#>
#>
#> $`G2:D3`
#> $`G2:D3`$overall
#> N mean_total.score sd_total.score ave.r sd.r alpha SEM.alpha
#> 500 4.45 2.794 0.12 0.066 0.667 1.612
#>
#> $`G2:D3`$itemstats
#> N mean sd total.r total.r_if_rm alpha_if_rm
#> Item_1 500 0.348 0.477 0.409 0.252 0.655
#> Item_2 500 0.230 0.421 0.423 0.287 0.650
#> Item_3 500 0.164 0.371 0.488 0.377 0.641
#> Item_4 500 0.306 0.461 0.216 0.052 0.683
#> Item_5 500 0.616 0.487 0.529 0.386 0.635
#> Item_6 500 0.330 0.471 0.509 0.367 0.639
#> Item_7 500 0.254 0.436 0.368 0.223 0.659
#> Item_8 500 0.248 0.432 0.395 0.253 0.655
#> Item_9 500 0.416 0.493 0.419 0.258 0.655
#> Item_10 500 0.258 0.438 0.381 0.236 0.657
#> Item_11 500 0.190 0.393 0.389 0.261 0.654
#> Item_12 500 0.410 0.492 0.447 0.290 0.650
#> Item_13 500 0.208 0.406 0.380 0.246 0.656
#> Item_14 500 0.276 0.447 0.477 0.340 0.643
#> Item_15 500 0.196 0.397 0.496 0.378 0.640
#>
#> $`G2:D3`$proportions
#> 0 1
#> Item_1 0.652 0.348
#> Item_2 0.770 0.230
#> Item_3 0.836 0.164
#> Item_4 0.694 0.306
#> Item_5 0.384 0.616
#> Item_6 0.670 0.330
#> Item_7 0.746 0.254
#> Item_8 0.752 0.248
#> Item_9 0.584 0.416
#> Item_10 0.742 0.258
#> Item_11 0.810 0.190
#> Item_12 0.590 0.410
#> Item_13 0.792 0.208
#> Item_14 0.724 0.276
#> Item_15 0.804 0.196
#>
#>
mod <- multipleGroup(dat, group = group, SE=TRUE,
invariance = c(colnames(dat), 'free_mean', 'free_var'))
coef(mod, simplify=TRUE)
#> $`G1:D1`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $`G1:D2`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> -0.073
#>
#> $cov
#> F1
#> F1 1.014
#>
#>
#> $`G1:D3`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> 0.058
#>
#> $cov
#> F1
#> F1 0.906
#>
#>
#> $`G2:D1`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> 0.489
#>
#> $cov
#> F1
#> F1 1.073
#>
#>
#> $`G2:D2`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> 0.496
#>
#> $cov
#> F1
#> F1 1.051
#>
#>
#> $`G2:D3`
#> $items
#> a1 d g u
#> Item_1 0.651 -0.080 0 1
#> Item_2 1.111 -0.388 0 1
#> Item_3 1.355 -0.622 0 1
#> Item_4 0.274 -0.549 0 1
#> Item_5 1.155 1.722 0 1
#> Item_6 1.110 0.137 0 1
#> Item_7 0.797 -0.314 0 1
#> Item_8 0.852 -0.302 0 1
#> Item_9 0.693 0.371 0 1
#> Item_10 0.698 -0.428 0 1
#> Item_11 0.816 -1.000 0 1
#> Item_12 0.761 0.428 0 1
#> Item_13 0.739 -0.715 0 1
#> Item_14 1.143 0.052 0 1
#> Item_15 1.218 -0.635 0 1
#>
#> $means
#> F1
#> -1.03
#>
#> $cov
#> F1
#> F1 1.047
#>
#>
sapply(coef(mod, simplify=TRUE), \(x) unname(x$means)) # mean estimates
#> G1:D1 G1:D2 G1:D3 G2:D1 G2:D2 G2:D3
#> 0.00000000 -0.07322592 0.05819135 0.48937111 0.49572481 -1.02999130
wald(mod) # view parameter names for later testing
#> a1.1.63.125.187.249.311 d.2.64.126.188.250.312 a1.5.67.129.191.253.315
#> 0.651 -0.080 1.111
#> d.6.68.130.192.254.316 a1.9.71.133.195.257.319 d.10.72.134.196.258.320
#> -0.388 1.355 -0.622
#> a1.13.75.137.199.261.323 d.14.76.138.200.262.324 a1.17.79.141.203.265.327
#> 0.274 -0.549 1.155
#> d.18.80.142.204.266.328 a1.21.83.145.207.269.331 d.22.84.146.208.270.332
#> 1.722 1.110 0.137
#> a1.25.87.149.211.273.335 d.26.88.150.212.274.336 a1.29.91.153.215.277.339
#> 0.797 -0.314 0.852
#> d.30.92.154.216.278.340 a1.33.95.157.219.281.343 d.34.96.158.220.282.344
#> -0.302 0.693 0.371
#> a1.37.99.161.223.285.347 d.38.100.162.224.286.348 a1.41.103.165.227.289.351
#> 0.698 -0.428 0.816
#> d.42.104.166.228.290.352 a1.45.107.169.231.293.355 d.46.108.170.232.294.356
#> -1.000 0.761 0.428
#> a1.49.111.173.235.297.359 d.50.112.174.236.298.360 a1.53.115.177.239.301.363
#> 0.739 -0.715 1.143
#> d.54.116.178.240.302.364 a1.57.119.181.243.305.367 d.58.120.182.244.306.368
#> 0.052 1.218 -0.635
#> MEAN_1.123 COV_11.124 MEAN_1.185
#> -0.073 1.014 0.058
#> COV_11.186 MEAN_1.247 COV_11.248
#> 0.906 0.489 1.073
#> MEAN_1.309 COV_11.310 MEAN_1.371
#> 0.496 1.051 -1.030
#> COV_11.372
#> 1.047
# test for main effect over G group (manually compute marginal mean)
wald(mod, "0 + MEAN_1.123 + MEAN_1.185 = MEAN_1.247 + MEAN_1.309 + MEAN_1.371")
#> W df p
#> 1 0.05078909 1 0.8216958
# test for main effect over D group (manually compute marginal means)
wald(mod, c("0 + MEAN_1.247 = MEAN_1.123 + MEAN_1.309",
"0 + MEAN_1.247 = MEAN_1.185 + MEAN_1.371"))
#> W df p
#> 1 146.5313 2 0
# post-hoc tests (better practice would include p.adjust() )
wald(mod, "0 + MEAN_1.247 = MEAN_1.123 + MEAN_1.309") # D1 vs D2
#> W df p
#> 1 0.3832815 1 0.5358523
wald(mod, "0 + MEAN_1.247 = MEAN_1.185 + MEAN_1.371") # D1 vs D3
#> W df p
#> 1 124.3293 1 0
wald(mod, "MEAN_1.123 + MEAN_1.309 = MEAN_1.185 + MEAN_1.371") # D2 vs D3
#> W df p
#> 1 117.8156 1 0
#############
# multiple factors
a <- matrix(c(abs(rnorm(5,1,.3)), rep(0,15),abs(rnorm(5,1,.3)),
rep(0,15),abs(rnorm(5,1,.3))), 15, 3)
d <- matrix(rnorm(15,0,.7),ncol=1)
mu <- c(-.4, -.7, .1)
sigma <- matrix(c(1.21,.297,1.232,.297,.81,.252,1.232,.252,1.96),3,3)
itemtype <- rep('2PL', nrow(a))
N <- 1000
dataset1 <- simdata(a, d, N, itemtype)
dataset2 <- simdata(a, d, N, itemtype, mu = mu, sigma = sigma)
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
# group models
model <- '
F1 = 1-5
F2 = 6-10
F3 = 11-15'
# define mirt cluster to use parallel architecture
if(interactive()) mirtCluster()
# EM approach (not as accurate with 3 factors, but generally good for quick model comparisons)
mod_configural <- multipleGroup(dat, model, group = group) #completely separate analyses
mod_metric <- multipleGroup(dat, model, group = group, invariance=c('slopes')) #equal slopes
mod_fullconstrain <- multipleGroup(dat, model, group = group, #equal means, slopes, intercepts
invariance=c('slopes', 'intercepts'))
anova(mod_metric, mod_configural)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_metric 36921.29 37030.37 37013.84 37173.33 -18415.65
#> mod_configural 36916.10 37061.53 37039.49 37252.15 -18398.05 35.197 15 0.002
anova(mod_fullconstrain, mod_metric)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_fullconstrain 37020.58 37093.29 37082.27 37188.60 -18480.29
#> mod_metric 36921.29 37030.37 37013.84 37173.33 -18415.65 129.284 15 0
# same as above, but with MHRM (generally more accurate with 3+ factors, but slower)
mod_configural <- multipleGroup(dat, model, group = group, method = 'MHRM')
mod_metric <- multipleGroup(dat, model, group = group, invariance=c('slopes'), method = 'MHRM')
mod_fullconstrain <- multipleGroup(dat, model, group = group, method = 'MHRM',
invariance=c('slopes', 'intercepts'))
anova(mod_metric, mod_configural)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_metric 36927.79 37036.86 37020.33 37179.83 -18418.89
#> mod_configural 36918.04 37063.47 37041.43 37254.10 -18399.02 39.745 15 0
anova(mod_fullconstrain, mod_metric)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_fullconstrain 37023.82 37096.54 37085.52 37191.85 -18481.91
#> mod_metric 36927.79 37036.86 37020.33 37179.83 -18418.89 126.04 15 0
############
# polytomous item example
set.seed(12345)
a <- matrix(abs(rnorm(15,1,.3)), ncol=1)
d <- matrix(rnorm(15,0,.7),ncol=1)
d <- cbind(d, d-1, d-2)
itemtype <- rep('graded', nrow(a))
N <- 1000
dataset1 <- simdata(a, d, N, itemtype)
dataset2 <- simdata(a, d, N, itemtype, mu = .1, sigma = matrix(1.5))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
model <- 'F1 = 1-15'
mod_configural <- multipleGroup(dat, model, group = group)
plot(mod_configural)
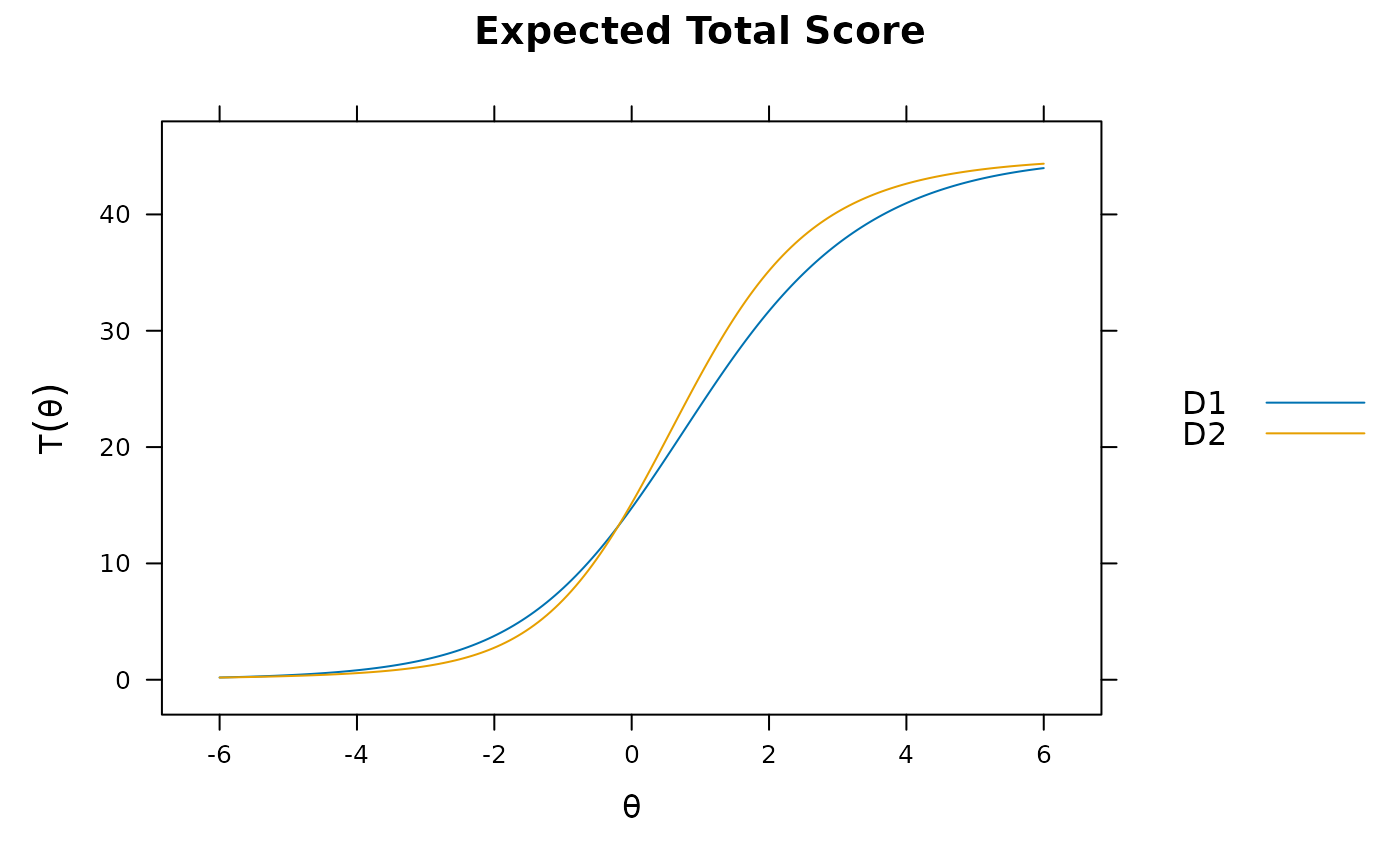plot(mod_configural, type = 'SE')
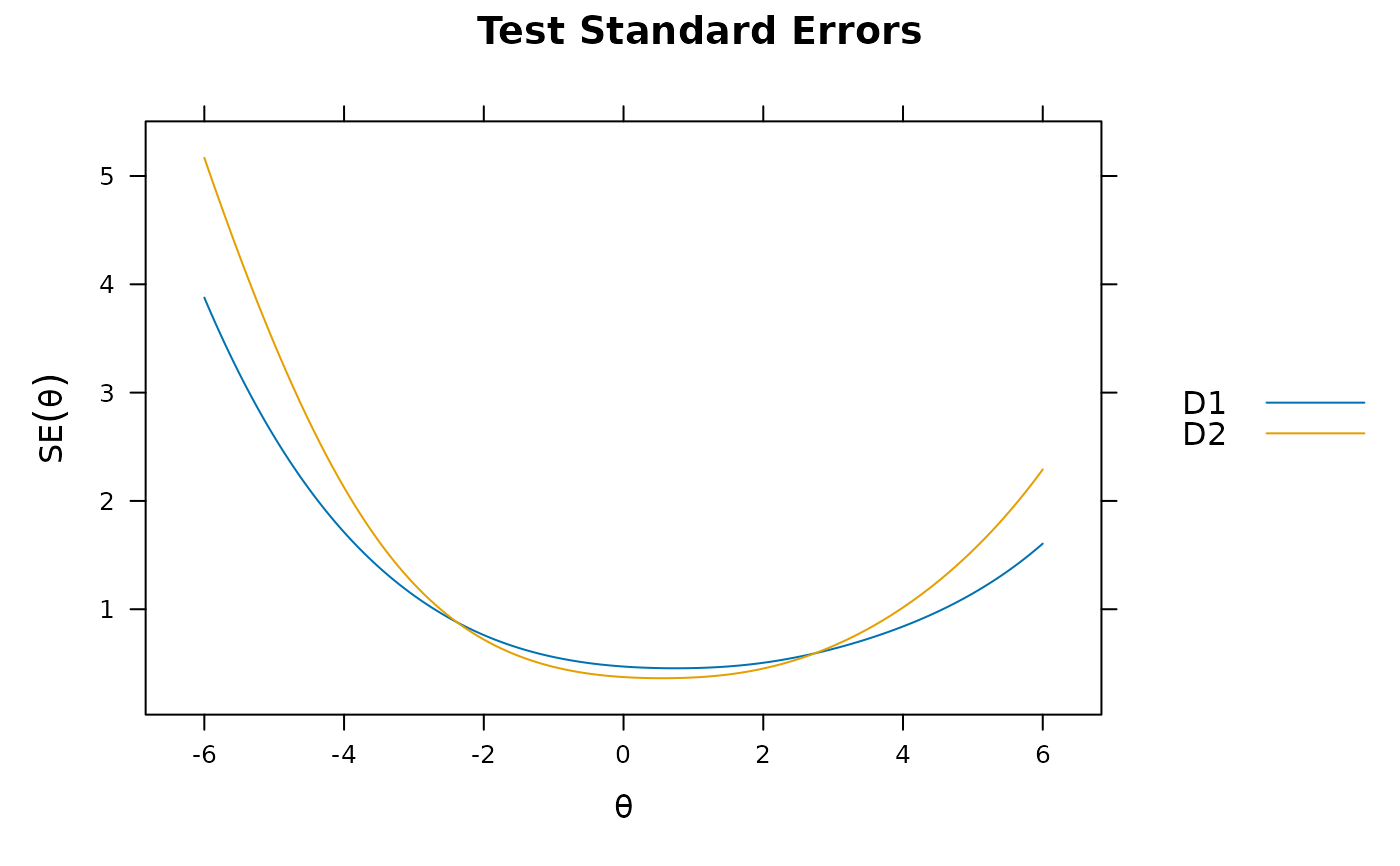itemplot(mod_configural, 1)
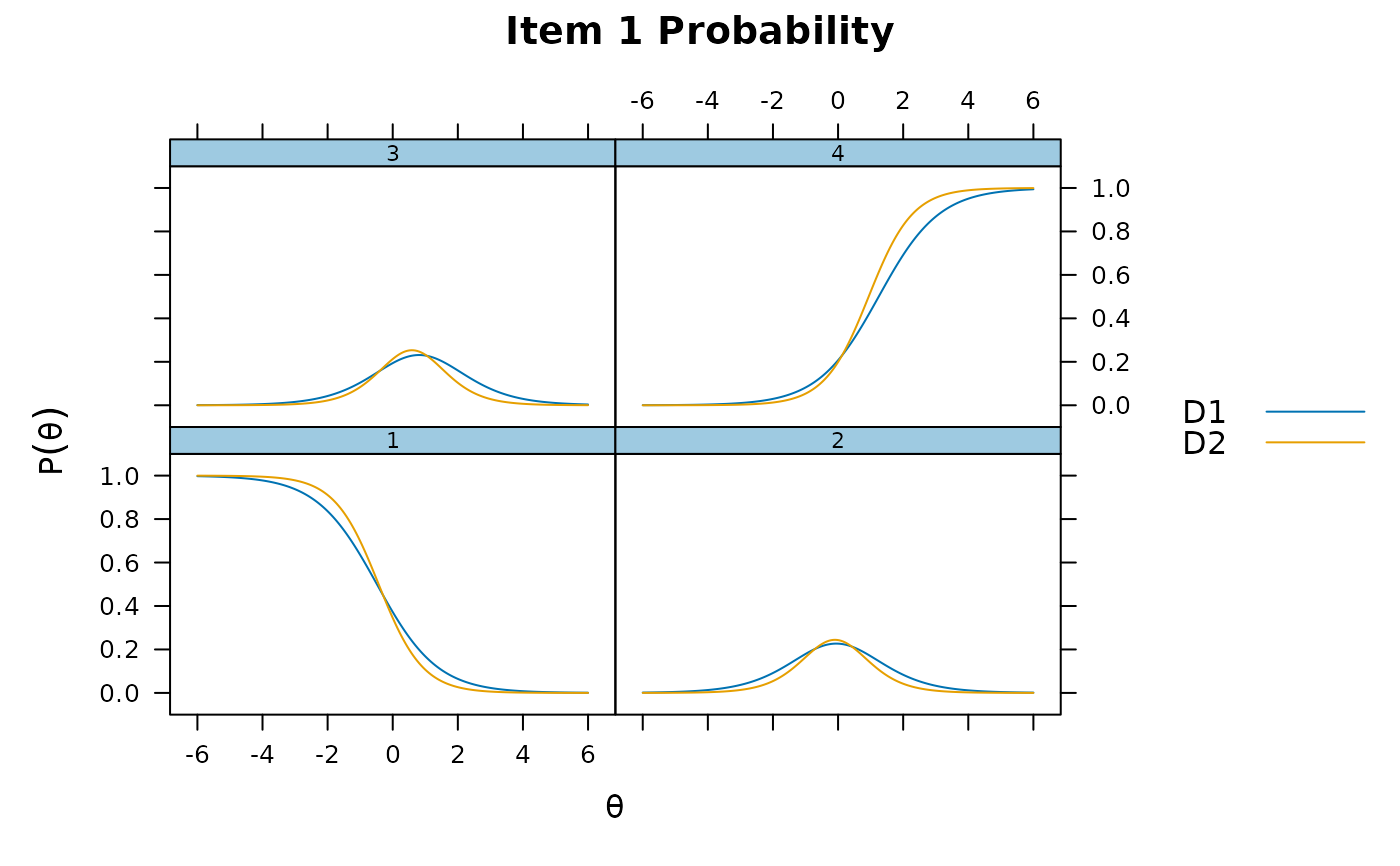itemplot(mod_configural, 1, type = 'info')
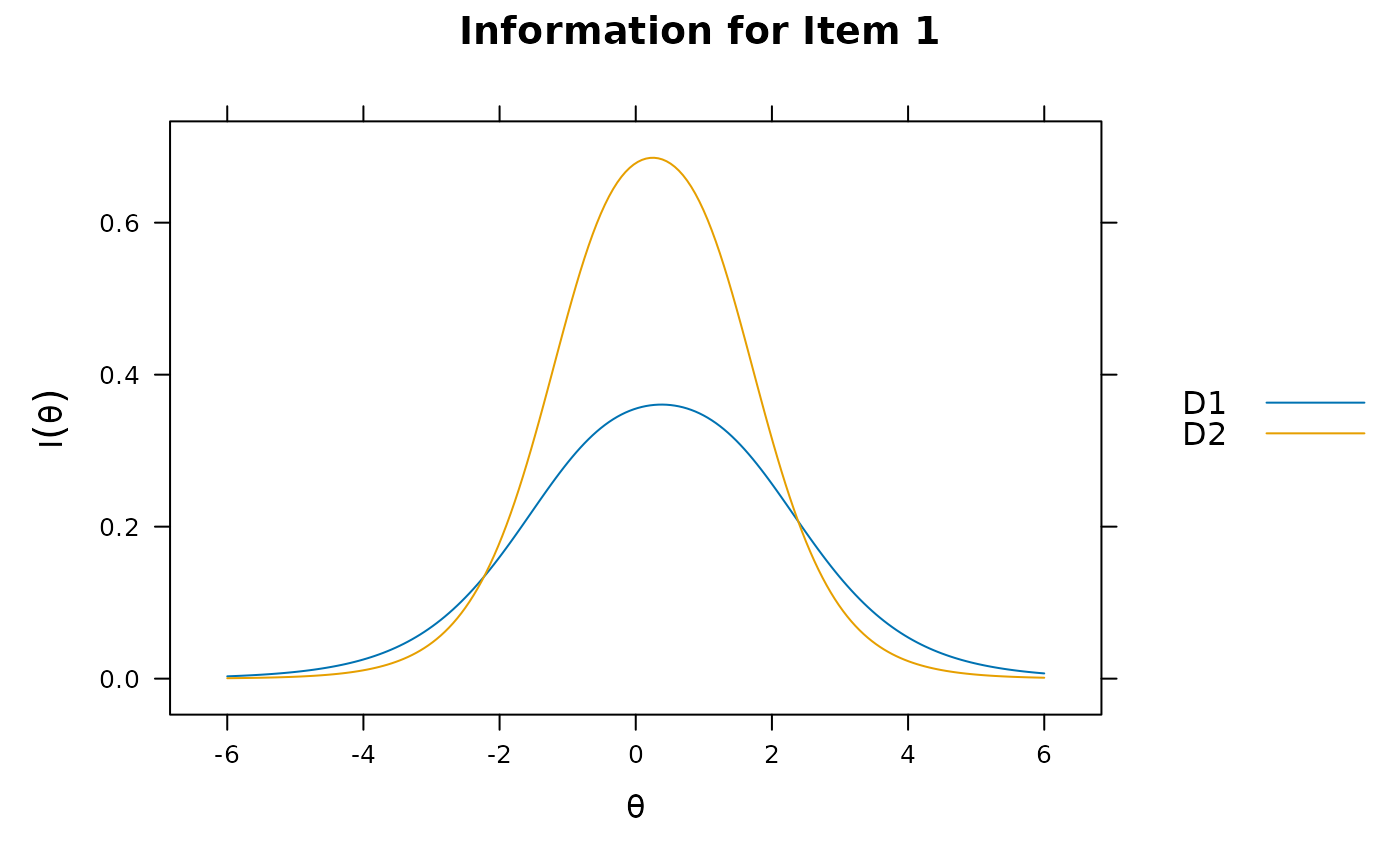plot(mod_configural, type = 'trace') # messy, score function typically better
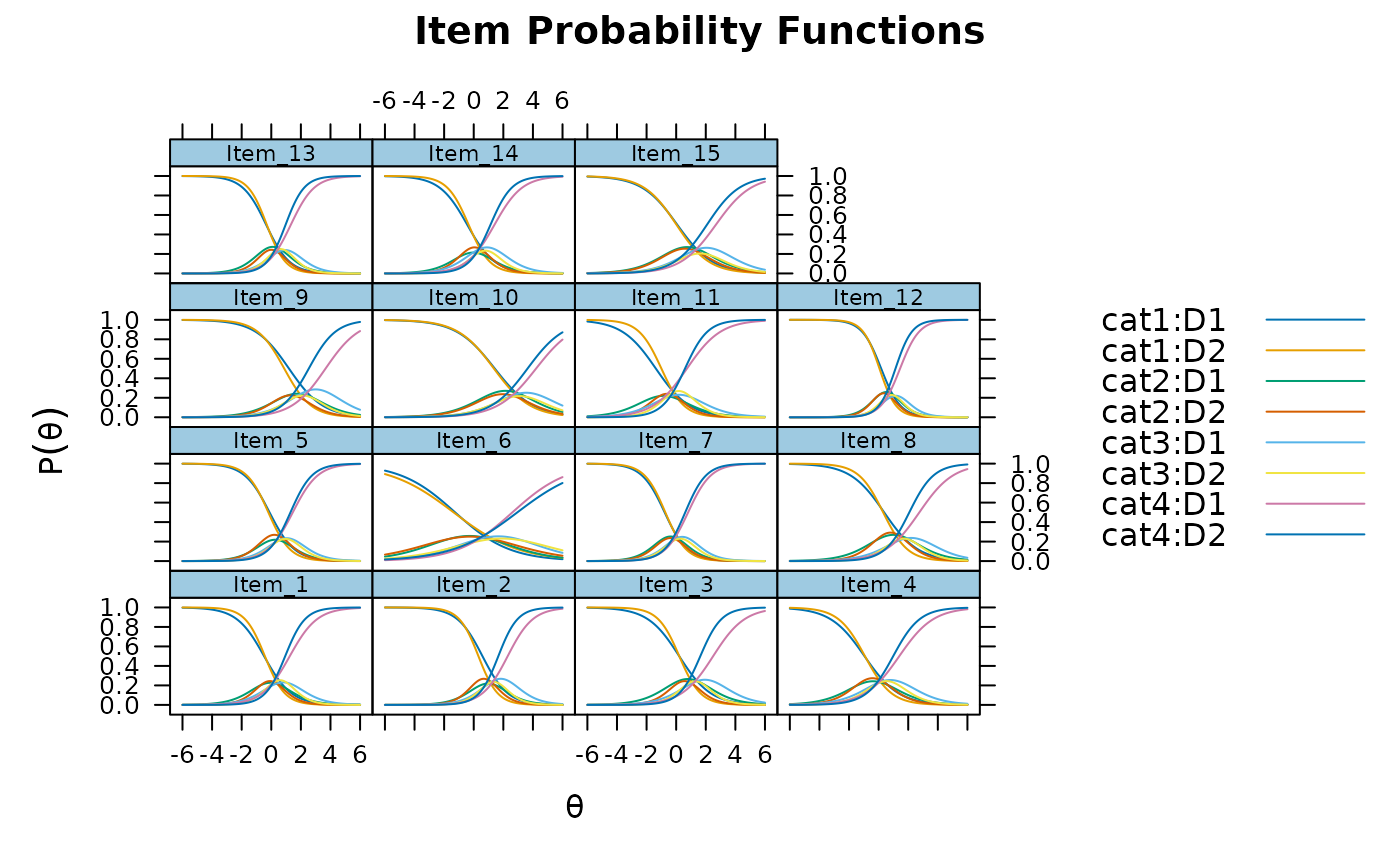plot(mod_configural, type = 'itemscore')
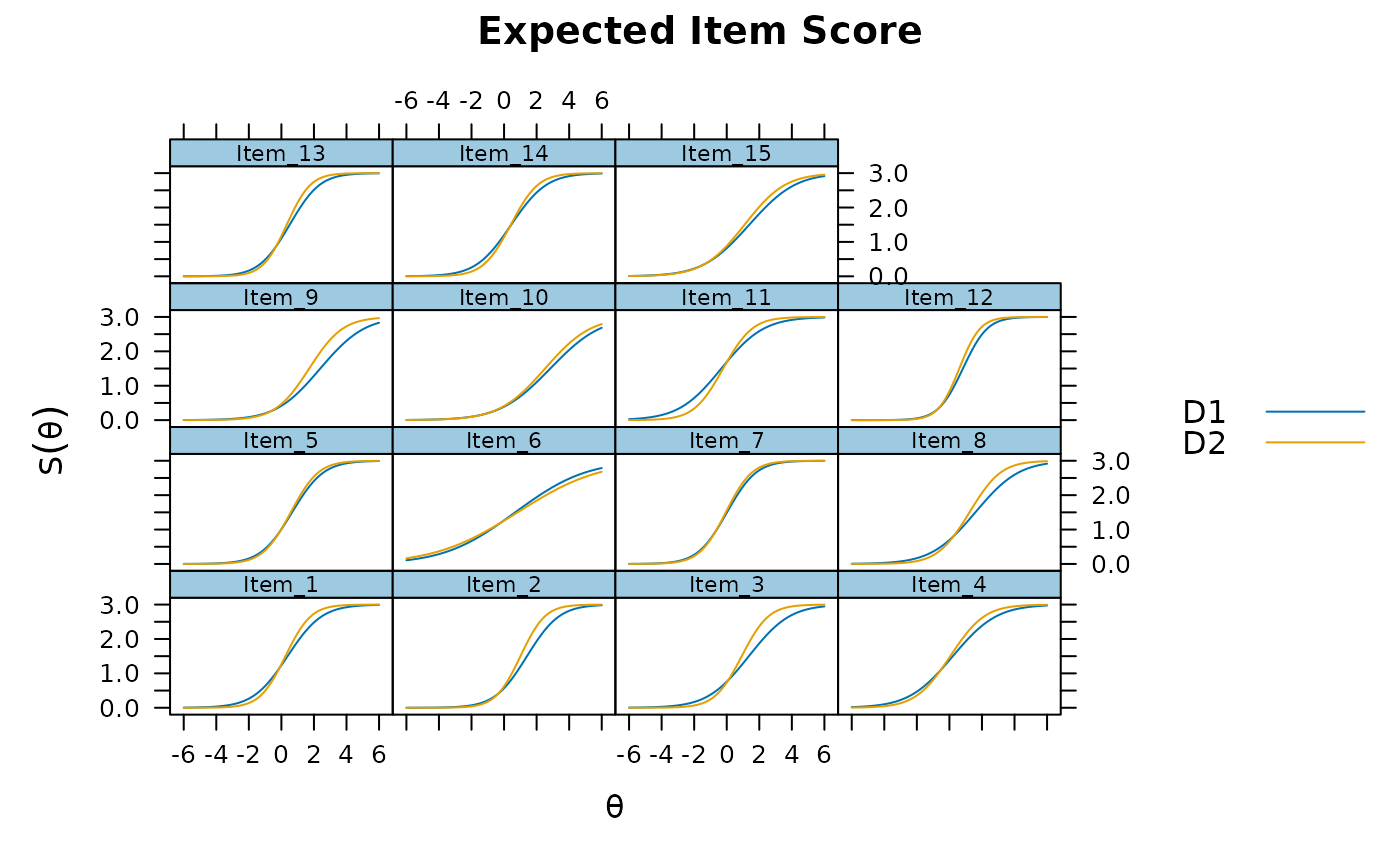fs <- fscores(mod_configural, full.scores = FALSE)
#>
#> Method: EAP
#>
#> Empirical Reliability:
#>
#> F1
#> 0.7942
#>
#> Method: EAP
#>
#> Empirical Reliability:
#>
#> F1
#> 0.7249
head(fs[["D1"]])
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> [1,] 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0
#> Item_11 Item_12 Item_13 Item_14 Item_15 F1 SE_F1
#> [1,] 0 0 0 0 0 -2.137056 0.6262714
#> [2,] 0 0 0 1 0 -1.785692 0.5741235
#> [3,] 0 0 0 2 0 -1.726621 0.5800312
#> [4,] 0 0 0 3 0 -1.688716 0.5856268
#> [5,] 0 0 0 3 1 -1.439230 0.5535499
#> [6,] 0 2 0 0 0 -1.582715 0.5660598
fscores(mod_configural, method = 'EAPsum', full.scores = FALSE)
#> df X2 p.X2 SEM.alpha rxx.alpha rxx_F1
#> stats 39 42.374 0.328 3.869 0.784 0.776
#>
#> df X2 p.X2 SEM.alpha rxx.alpha rxx_F1
#> stats 42 29.475 0.928 3.825 0.842 0.832
#>
#> $D1
#> Sum.Scores F1 SE_F1 observed expected std.res
#> 0 0 -2.137 0.626 6 5.731 0.112
#> 1 1 -1.842 0.589 6 10.082 1.286
#> 2 2 -1.645 0.575 19 15.026 1.025
#> 3 3 -1.491 0.568 22 21.117 0.192
#> 4 4 -1.323 0.548 31 26.167 0.945
#> 5 5 -1.173 0.534 21 30.811 1.768
#> 6 6 -1.033 0.523 30 34.974 0.841
#> 7 7 -0.898 0.510 37 38.286 0.208
#> 8 8 -0.770 0.500 47 40.921 0.950
#> 9 9 -0.648 0.490 40 42.896 0.442
#> 10 10 -0.531 0.481 54 44.208 1.473
#> 11 11 -0.417 0.473 52 44.945 1.052
#> 12 12 -0.307 0.466 50 45.161 0.720
#> 13 13 -0.201 0.460 35 44.909 1.479
#> 14 14 -0.097 0.455 41 44.252 0.489
#> 15 15 0.005 0.450 33 43.244 1.558
#> 16 16 0.104 0.446 50 41.936 1.245
#> 17 17 0.202 0.443 38 40.375 0.374
#> 18 18 0.298 0.440 34 38.606 0.741
#> 19 19 0.394 0.437 40 36.668 0.550
#> 20 20 0.488 0.436 30 34.599 0.782
#> 21 21 0.582 0.435 42 32.431 1.680
#> 22 22 0.675 0.434 32 30.195 0.328
#> 23 23 0.768 0.434 28 27.920 0.015
#> 24 24 0.861 0.434 19 25.631 1.310
#> 25 25 0.954 0.435 34 23.350 2.204
#> 26 26 1.048 0.436 21 21.099 0.022
#> 27 27 1.142 0.438 18 18.899 0.207
#> 28 28 1.237 0.441 21 16.765 1.034
#> 29 29 1.334 0.444 10 14.717 1.229
#> 30 30 1.431 0.447 11 12.767 0.495
#> 31 31 1.530 0.451 8 10.931 0.887
#> 32 32 1.631 0.456 8 9.221 0.402
#> 33 33 1.733 0.461 8 7.648 0.127
#> 34 34 1.838 0.466 6 6.221 0.089
#> 35 35 1.946 0.472 1 4.949 1.775
#> 36 36 2.056 0.479 4 3.835 0.084
#> 37 37 2.169 0.486 6 2.881 1.838
#> 38 38 2.287 0.494 3 2.086 0.632
#> 39 39 2.409 0.503 3 1.445 1.293
#> 40 40 2.535 0.512 1 0.946 0.055
#> 41 41 2.668 0.522 0 0.580 0.761
#> 42 42 2.809 0.534 0 0.324 0.569
#> 43 43 2.955 0.544 0 0.158 0.397
#> 44 44 3.126 0.559 0 0.066 0.256
#> 45 45 3.345 0.584 0 0.019 0.137
#>
#> $D2
#> Sum.Scores F1 SE_F1 observed expected std.res
#> 0 0 -2.051 0.591 9 11.036 0.613
#> 1 1 -1.750 0.548 23 16.140 1.708
#> 2 2 -1.554 0.530 22 20.995 0.219
#> 3 3 -1.412 0.524 31 27.050 0.759
#> 4 4 -1.240 0.493 35 30.434 0.828
#> 5 5 -1.095 0.475 33 33.197 0.034
#> 6 6 -0.964 0.460 34 35.476 0.248
#> 7 7 -0.836 0.444 32 36.880 0.804
#> 8 8 -0.718 0.431 32 37.812 0.945
#> 9 9 -0.607 0.419 31 38.353 1.187
#> 10 10 -0.501 0.409 28 38.516 1.695
#> 11 11 -0.400 0.400 46 38.404 1.226
#> 12 12 -0.303 0.393 41 38.063 0.476
#> 13 13 -0.210 0.386 36 37.526 0.249
#> 14 14 -0.119 0.381 33 36.830 0.631
#> 15 15 -0.031 0.376 37 36.003 0.166
#> 16 16 0.055 0.372 33 35.064 0.349
#> 17 17 0.140 0.369 33 34.032 0.177
#> 18 18 0.223 0.366 42 32.921 1.582
#> 19 19 0.305 0.364 28 31.744 0.665
#> 20 20 0.386 0.363 29 30.511 0.274
#> 21 21 0.466 0.362 30 29.230 0.142
#> 22 22 0.546 0.362 24 27.908 0.740
#> 23 23 0.626 0.362 28 26.553 0.281
#> 24 24 0.706 0.363 29 25.169 0.764
#> 25 25 0.787 0.364 27 23.761 0.664
#> 26 26 0.868 0.366 29 22.334 1.411
#> 27 27 0.950 0.369 19 20.892 0.414
#> 28 28 1.033 0.372 17 19.437 0.553
#> 29 29 1.117 0.376 13 17.975 1.174
#> 30 30 1.203 0.380 19 16.510 0.613
#> 31 31 1.291 0.385 17 15.044 0.504
#> 32 32 1.381 0.391 17 13.583 0.927
#> 33 33 1.473 0.398 16 12.135 1.109
#> 34 34 1.568 0.405 11 10.703 0.091
#> 35 35 1.667 0.414 8 9.299 0.426
#> 36 36 1.769 0.423 11 7.936 1.088
#> 37 37 1.874 0.433 3 6.617 1.406
#> 38 38 1.984 0.444 6 5.370 0.272
#> 39 39 2.101 0.457 4 4.219 0.107
#> 40 40 2.219 0.469 2 3.152 0.649
#> 41 41 2.344 0.482 2 2.236 0.158
#> 42 42 2.484 0.501 0 1.485 1.219
#> 43 43 2.612 0.511 0 0.842 0.918
#> 44 44 2.766 0.525 0 0.438 0.662
#> 45 45 2.988 0.555 0 0.185 0.431
#>
# constrain slopes within each group to be equal (but not across groups)
model2 <- 'F1 = 1-15
CONSTRAIN = (1-15, a1)'
mod_configural2 <- multipleGroup(dat, model2, group = group)
plot(mod_configural2, type = 'SE')
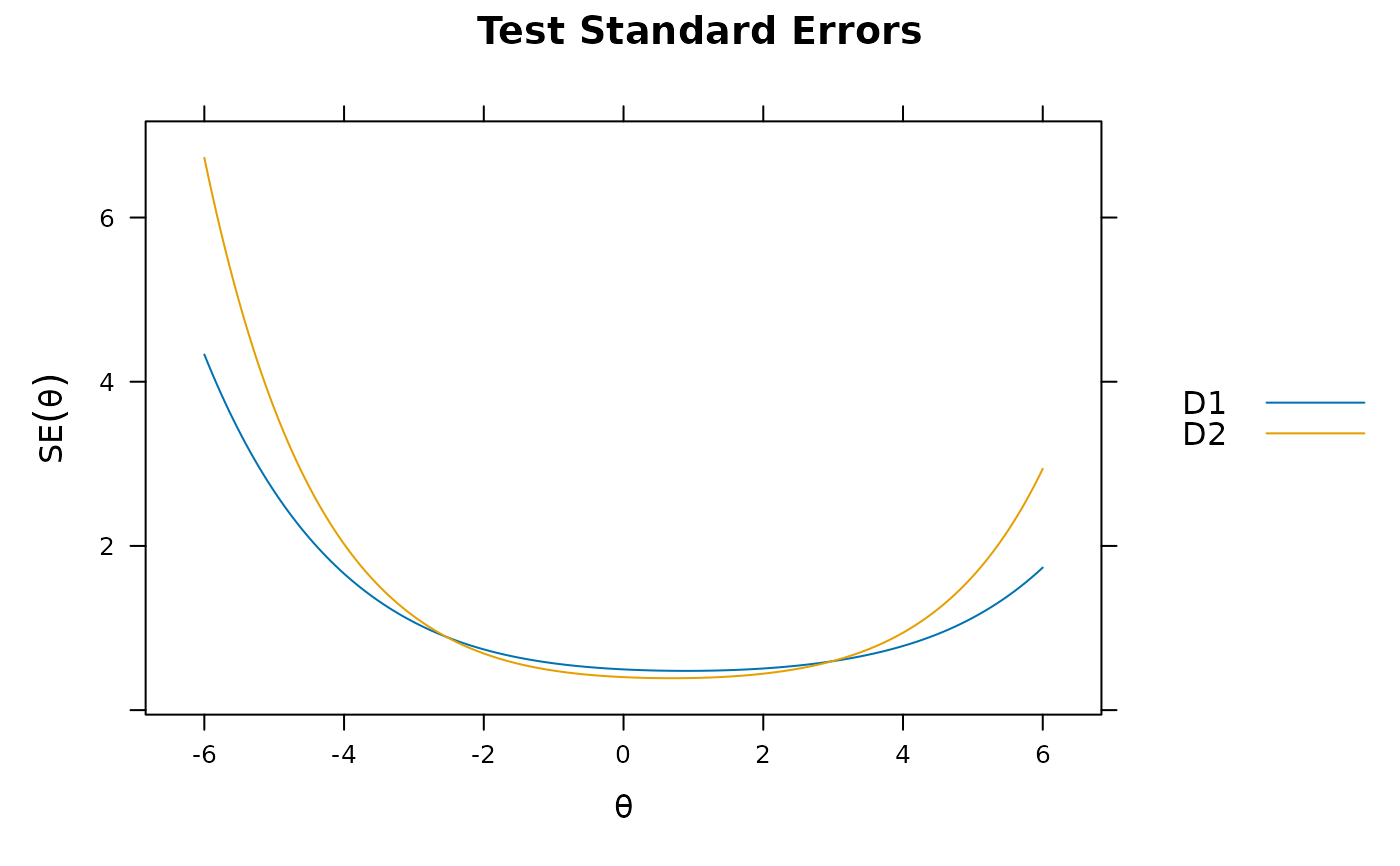plot(mod_configural2, type = 'RE')
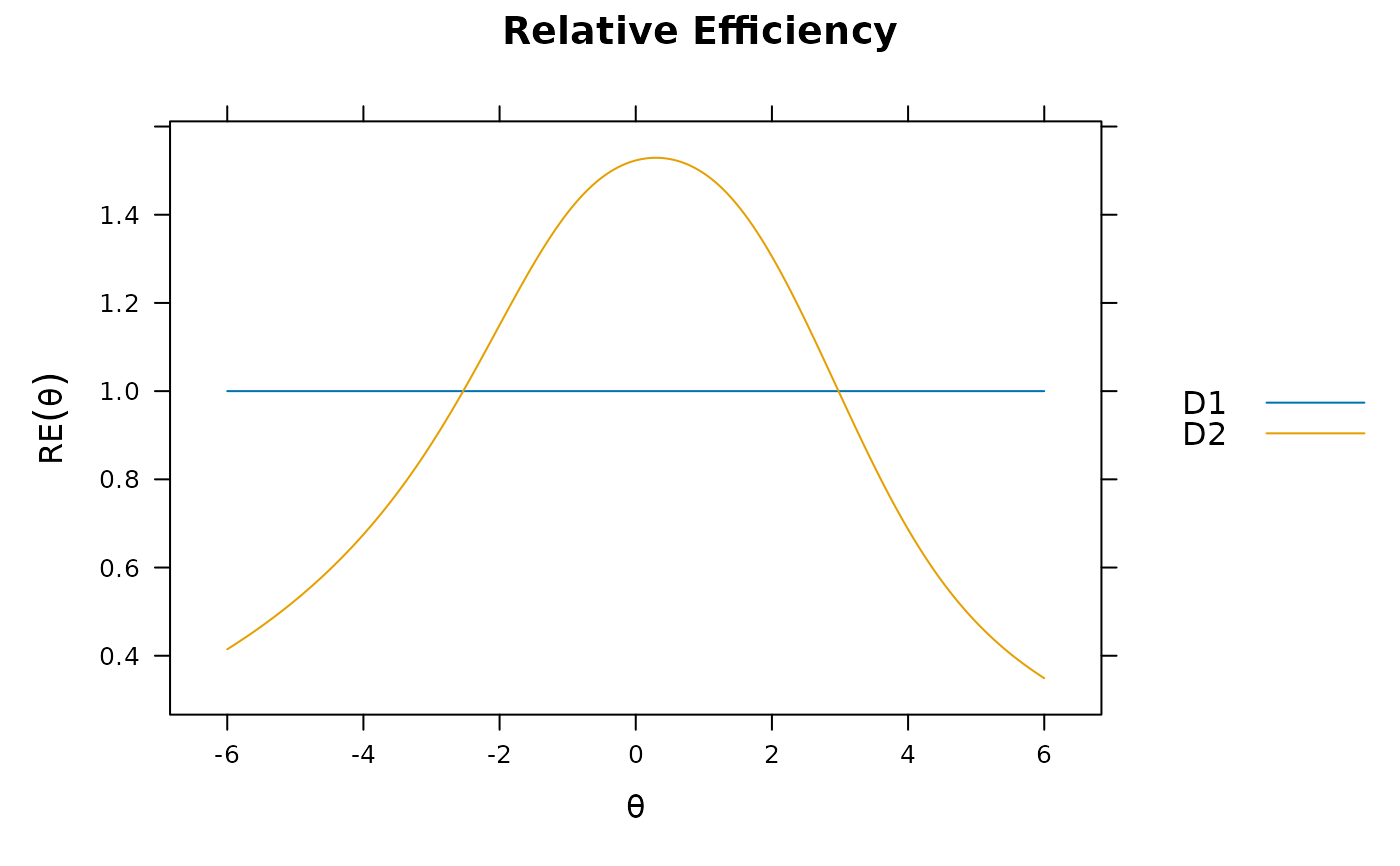itemplot(mod_configural2, 10)
############
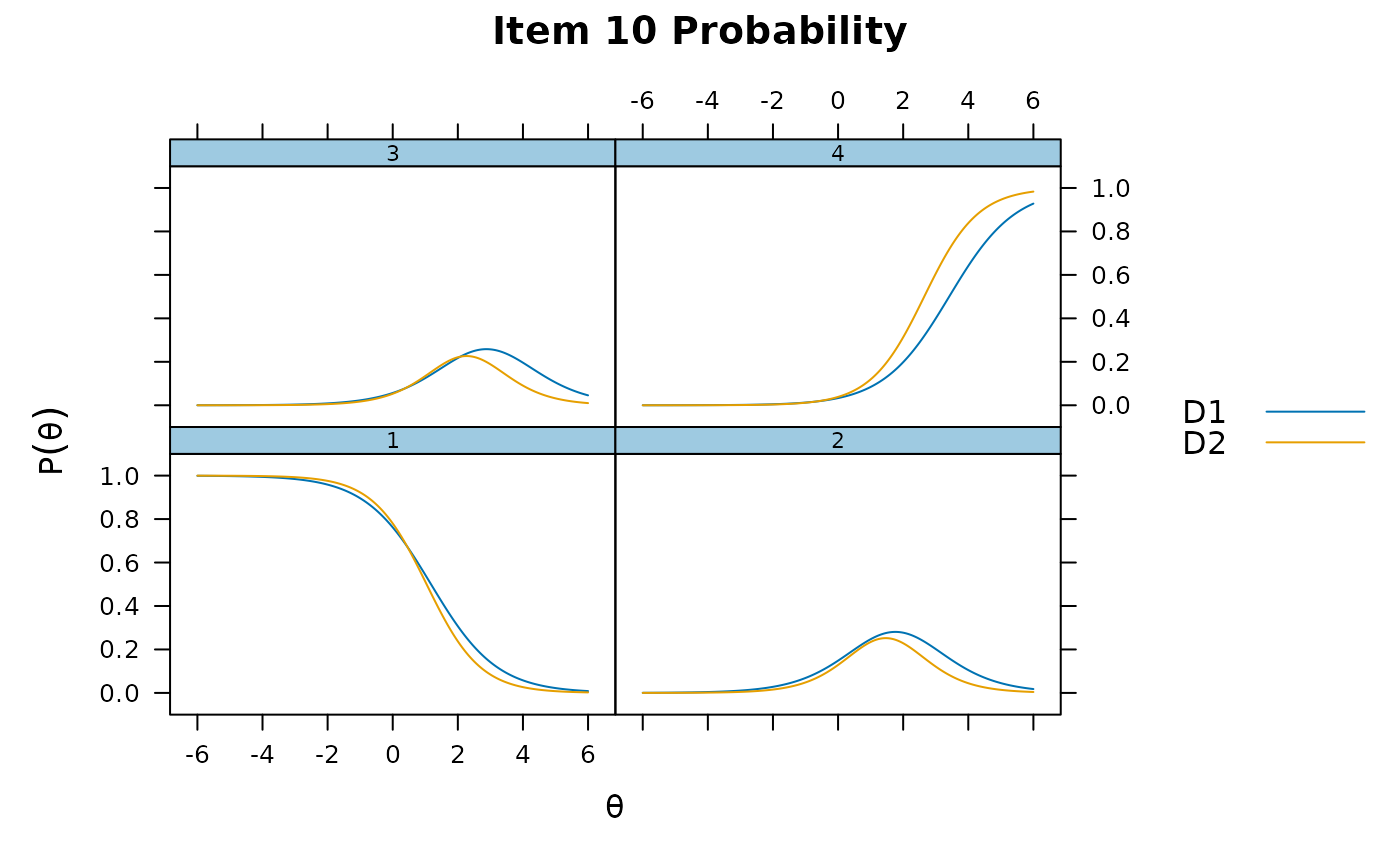## empirical histogram example (normal and bimodal groups)
set.seed(1234)
a <- matrix(rlnorm(50, .2, .2))
d <- matrix(rnorm(50))
ThetaNormal <- matrix(rnorm(2000))
ThetaBimodal <- scale(matrix(c(rnorm(1000, -2), rnorm(1000,2)))) #bimodal
Theta <- rbind(ThetaNormal, ThetaBimodal)
dat <- simdata(a, d, 4000, itemtype = '2PL', Theta=Theta)
group <- rep(c('G1', 'G2'), each=2000)
EH <- multipleGroup(dat, 1, group=group, dentype="empiricalhist", invariance = colnames(dat))
coef(EH, simplify=TRUE)
#> $G1
#> $items
#> a1 d g u
#> Item_1 0.759 -1.830 0 1
#> Item_2 1.062 -0.555 0 1
#> Item_3 1.235 -1.117 0 1
#> Item_4 0.611 -0.953 0 1
#> Item_5 1.088 -0.132 0 1
#> Item_6 1.054 0.502 0 1
#> Item_7 0.849 1.581 0 1
#> Item_8 0.870 -0.779 0 1
#> Item_9 0.902 1.658 0 1
#> Item_10 0.812 -1.188 0 1
#> Item_11 0.903 0.661 0 1
#> Item_12 0.841 2.646 0 1
#> Item_13 0.843 -0.064 0 1
#> Item_14 1.009 -0.600 0 1
#> Item_15 1.167 0.013 0 1
#> Item_16 1.008 1.886 0 1
#> Item_17 0.885 -1.124 0 1
#> Item_18 0.790 1.420 0 1
#> Item_19 0.799 1.316 0 1
#> Item_20 1.565 0.294 0 1
#> Item_21 1.002 0.001 0 1
#> Item_22 0.929 -0.497 0 1
#> Item_23 0.903 -0.383 0 1
#> Item_24 1.120 0.702 0 1
#> Item_25 0.850 2.002 0 1
#> Item_26 0.706 -0.208 0 1
#> Item_27 1.048 -1.279 0 1
#> Item_28 0.826 -0.770 0 1
#> Item_29 1.062 0.221 0 1
#> Item_30 0.737 -0.333 0 1
#> Item_31 1.208 -0.178 0 1
#> Item_32 0.917 -0.202 0 1
#> Item_33 0.859 -1.360 0 1
#> Item_34 0.913 -0.252 0 1
#> Item_35 0.767 0.886 0 1
#> Item_36 0.783 0.763 0 1
#> Item_37 0.630 0.550 0 1
#> Item_38 0.736 -0.405 0 1
#> Item_39 0.917 -0.166 0 1
#> Item_40 0.895 -1.251 0 1
#> Item_41 1.251 -0.040 0 1
#> Item_42 0.882 0.202 0 1
#> Item_43 0.796 1.639 0 1
#> Item_44 1.022 1.038 0 1
#> Item_45 0.812 -0.470 0 1
#> Item_46 0.807 0.336 0 1
#> Item_47 0.815 -1.121 0 1
#> Item_48 0.739 0.892 0 1
#> Item_49 0.904 1.036 0 1
#> Item_50 0.895 2.124 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $G2
#> $items
#> a1 d g u
#> Item_1 0.759 -1.830 0 1
#> Item_2 1.062 -0.555 0 1
#> Item_3 1.235 -1.117 0 1
#> Item_4 0.611 -0.953 0 1
#> Item_5 1.088 -0.132 0 1
#> Item_6 1.054 0.502 0 1
#> Item_7 0.849 1.581 0 1
#> Item_8 0.870 -0.779 0 1
#> Item_9 0.902 1.658 0 1
#> Item_10 0.812 -1.188 0 1
#> Item_11 0.903 0.661 0 1
#> Item_12 0.841 2.646 0 1
#> Item_13 0.843 -0.064 0 1
#> Item_14 1.009 -0.600 0 1
#> Item_15 1.167 0.013 0 1
#> Item_16 1.008 1.886 0 1
#> Item_17 0.885 -1.124 0 1
#> Item_18 0.790 1.420 0 1
#> Item_19 0.799 1.316 0 1
#> Item_20 1.565 0.294 0 1
#> Item_21 1.002 0.001 0 1
#> Item_22 0.929 -0.497 0 1
#> Item_23 0.903 -0.383 0 1
#> Item_24 1.120 0.702 0 1
#> Item_25 0.850 2.002 0 1
#> Item_26 0.706 -0.208 0 1
#> Item_27 1.048 -1.279 0 1
#> Item_28 0.826 -0.770 0 1
#> Item_29 1.062 0.221 0 1
#> Item_30 0.737 -0.333 0 1
#> Item_31 1.208 -0.178 0 1
#> Item_32 0.917 -0.202 0 1
#> Item_33 0.859 -1.360 0 1
#> Item_34 0.913 -0.252 0 1
#> Item_35 0.767 0.886 0 1
#> Item_36 0.783 0.763 0 1
#> Item_37 0.630 0.550 0 1
#> Item_38 0.736 -0.405 0 1
#> Item_39 0.917 -0.166 0 1
#> Item_40 0.895 -1.251 0 1
#> Item_41 1.251 -0.040 0 1
#> Item_42 0.882 0.202 0 1
#> Item_43 0.796 1.639 0 1
#> Item_44 1.022 1.038 0 1
#> Item_45 0.812 -0.470 0 1
#> Item_46 0.807 0.336 0 1
#> Item_47 0.815 -1.121 0 1
#> Item_48 0.739 0.892 0 1
#> Item_49 0.904 1.036 0 1
#> Item_50 0.895 2.124 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
plot(EH, type = 'empiricalhist', npts = 60)
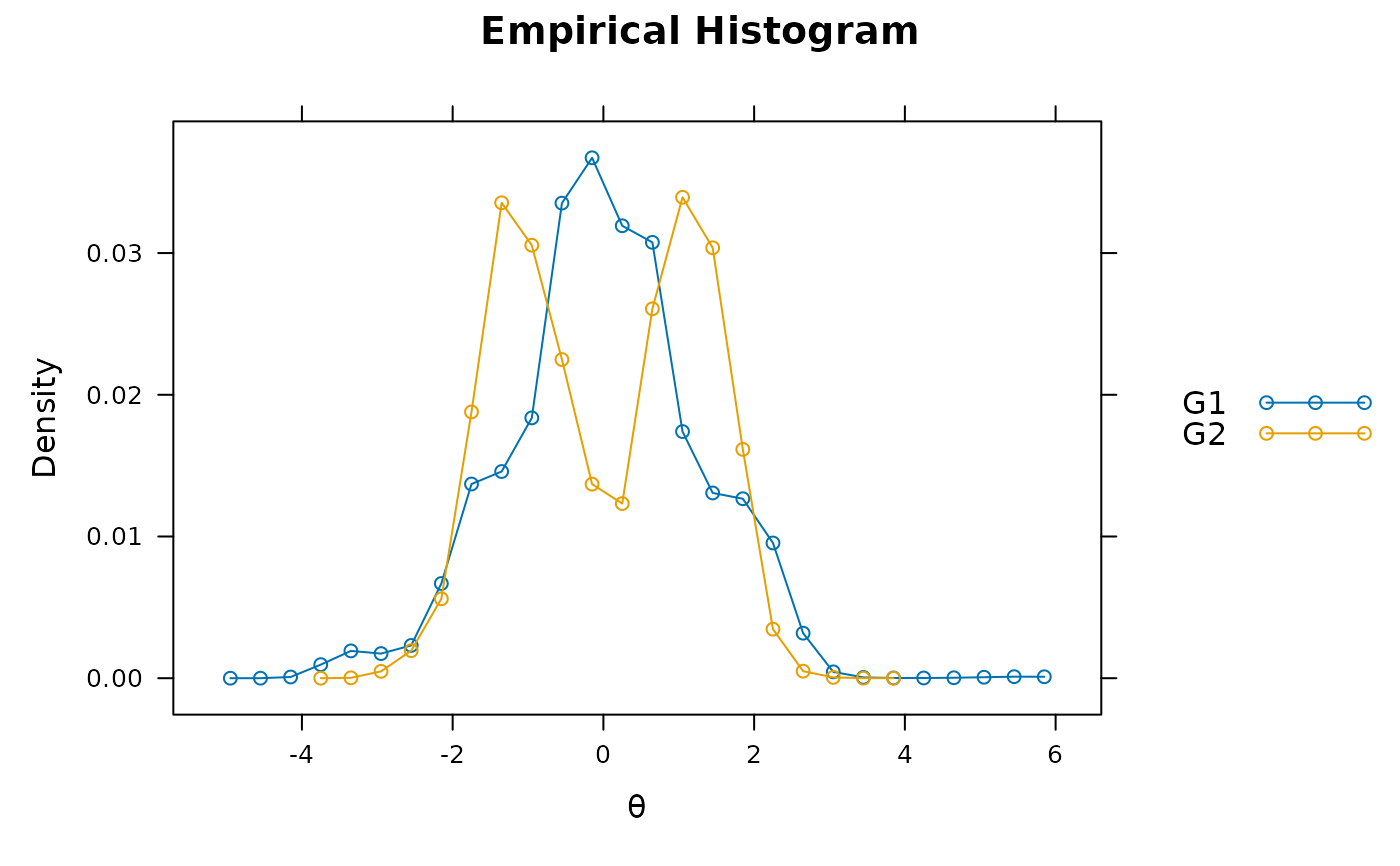# DIF test for item 1
EH1 <- multipleGroup(dat, 1, group=group, dentype="empiricalhist", invariance = colnames(dat)[-1])
anova(EH, EH1)
#> AIC SABIC HQ BIC logLik X2 df p
#> EH 216599.8 217659.4 217358.4 218739.8 -107959.9
#> EH1 216602.9 217668.7 217365.9 218755.4 -107959.4 0.916 2 0.632
#--------------------------------
# Mixture model (no prior group variable specified)
set.seed(12345)
nitems <- 20
a1 <- matrix(.75, ncol=1, nrow=nitems)
a2 <- matrix(1.25, ncol=1, nrow=nitems)
d1 <- matrix(rnorm(nitems,0,1),ncol=1)
d2 <- matrix(rnorm(nitems,0,1),ncol=1)
itemtype <- rep('2PL', nrow(a1))
N1 <- 500
N2 <- N1*2 # second class twice as large
dataset1 <- simdata(a1, d1, N1, itemtype)
dataset2 <- simdata(a2, d2, N2, itemtype)
dat <- rbind(dataset1, dataset2)
# group <- c(rep('D1', N1), rep('D2', N2))
# Mixture Rasch model (Rost, 1990)
models <- 'F1 = 1-20
CONSTRAIN = (1-20, a1)'
mod_mix <- multipleGroup(dat, models, dentype = 'mixture-2', GenRandomPars = TRUE)
coef(mod_mix, simplify=TRUE)
#> $MIXTURE_1
#> $items
#> a1 d g u
#> Item_1 1.302 0.772 0 1
#> Item_2 1.302 1.476 0 1
#> Item_3 1.302 -0.553 0 1
#> Item_4 1.302 -1.588 0 1
#> Item_5 1.302 -1.545 0 1
#> Item_6 1.302 2.084 0 1
#> Item_7 1.302 -0.510 0 1
#> Item_8 1.302 0.606 0 1
#> Item_9 1.302 0.550 0 1
#> Item_10 1.302 -0.167 0 1
#> Item_11 1.302 0.961 0 1
#> Item_12 1.302 2.156 0 1
#> Item_13 1.302 2.082 0 1
#> Item_14 1.302 1.733 0 1
#> Item_15 1.302 0.138 0 1
#> Item_16 1.302 0.434 0 1
#> Item_17 1.302 -0.368 0 1
#> Item_18 1.302 -1.633 0 1
#> Item_19 1.302 1.799 0 1
#> Item_20 1.302 -0.024 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#> $class_proportion
#> pi
#> 0.655
#>
#>
#> $MIXTURE_2
#> $items
#> a1 d g u
#> Item_1 0.681 0.664 0 1
#> Item_2 0.681 0.805 0 1
#> Item_3 0.681 -0.039 0 1
#> Item_4 0.681 -0.416 0 1
#> Item_5 0.681 0.530 0 1
#> Item_6 0.681 -2.045 0 1
#> Item_7 0.681 0.770 0 1
#> Item_8 0.681 -0.314 0 1
#> Item_9 0.681 -0.030 0 1
#> Item_10 0.681 -0.820 0 1
#> Item_11 0.681 -0.252 0 1
#> Item_12 0.681 1.939 0 1
#> Item_13 0.681 0.642 0 1
#> Item_14 0.681 0.593 0 1
#> Item_15 0.681 -0.749 0 1
#> Item_16 0.681 0.852 0 1
#> Item_17 0.681 -0.950 0 1
#> Item_18 0.681 -0.345 0 1
#> Item_19 0.681 1.230 0 1
#> Item_20 0.681 0.271 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#> $class_proportion
#> pi
#> 0.345
#>
#>
summary(mod_mix)
#>
#> ----------
#> GROUP: MIXTURE_1
#> F1 h2
#> Item_1 0.608 0.369
#> Item_2 0.608 0.369
#> Item_3 0.608 0.369
#> Item_4 0.608 0.369
#> Item_5 0.608 0.369
#> Item_6 0.608 0.369
#> Item_7 0.608 0.369
#> Item_8 0.608 0.369
#> Item_9 0.608 0.369
#> Item_10 0.608 0.369
#> Item_11 0.608 0.369
#> Item_12 0.608 0.369
#> Item_13 0.608 0.369
#> Item_14 0.608 0.369
#> Item_15 0.608 0.369
#> Item_16 0.608 0.369
#> Item_17 0.608 0.369
#> Item_18 0.608 0.369
#> Item_19 0.608 0.369
#> Item_20 0.608 0.369
#>
#> SS loadings: 7.386
#> Proportion Var: 0.369
#>
#> Factor correlations:
#>
#> F1
#> F1 1
#>
#> Class proportion: 0.655
#>
#> ----------
#> GROUP: MIXTURE_2
#> F1 h2
#> Item_1 0.371 0.138
#> Item_2 0.371 0.138
#> Item_3 0.371 0.138
#> Item_4 0.371 0.138
#> Item_5 0.371 0.138
#> Item_6 0.371 0.138
#> Item_7 0.371 0.138
#> Item_8 0.371 0.138
#> Item_9 0.371 0.138
#> Item_10 0.371 0.138
#> Item_11 0.371 0.138
#> Item_12 0.371 0.138
#> Item_13 0.371 0.138
#> Item_14 0.371 0.138
#> Item_15 0.371 0.138
#> Item_16 0.371 0.138
#> Item_17 0.371 0.138
#> Item_18 0.371 0.138
#> Item_19 0.371 0.138
#> Item_20 0.371 0.138
#>
#> SS loadings: 2.758
#> Proportion Var: 0.138
#>
#> Factor correlations:
#>
#> F1
#> F1 1
#>
#> Class proportion: 0.345
plot(mod_mix)
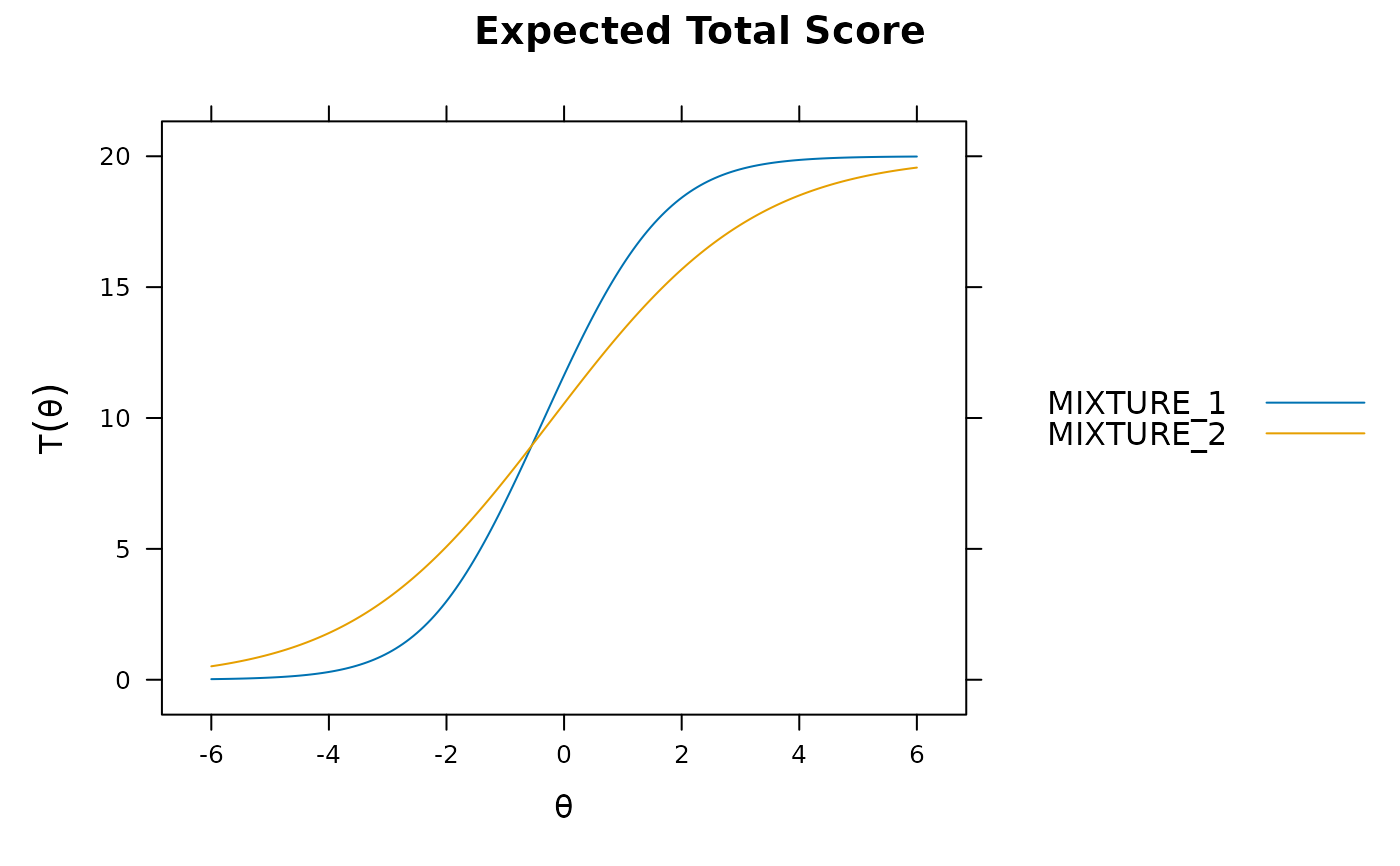plot(mod_mix, type = 'trace')
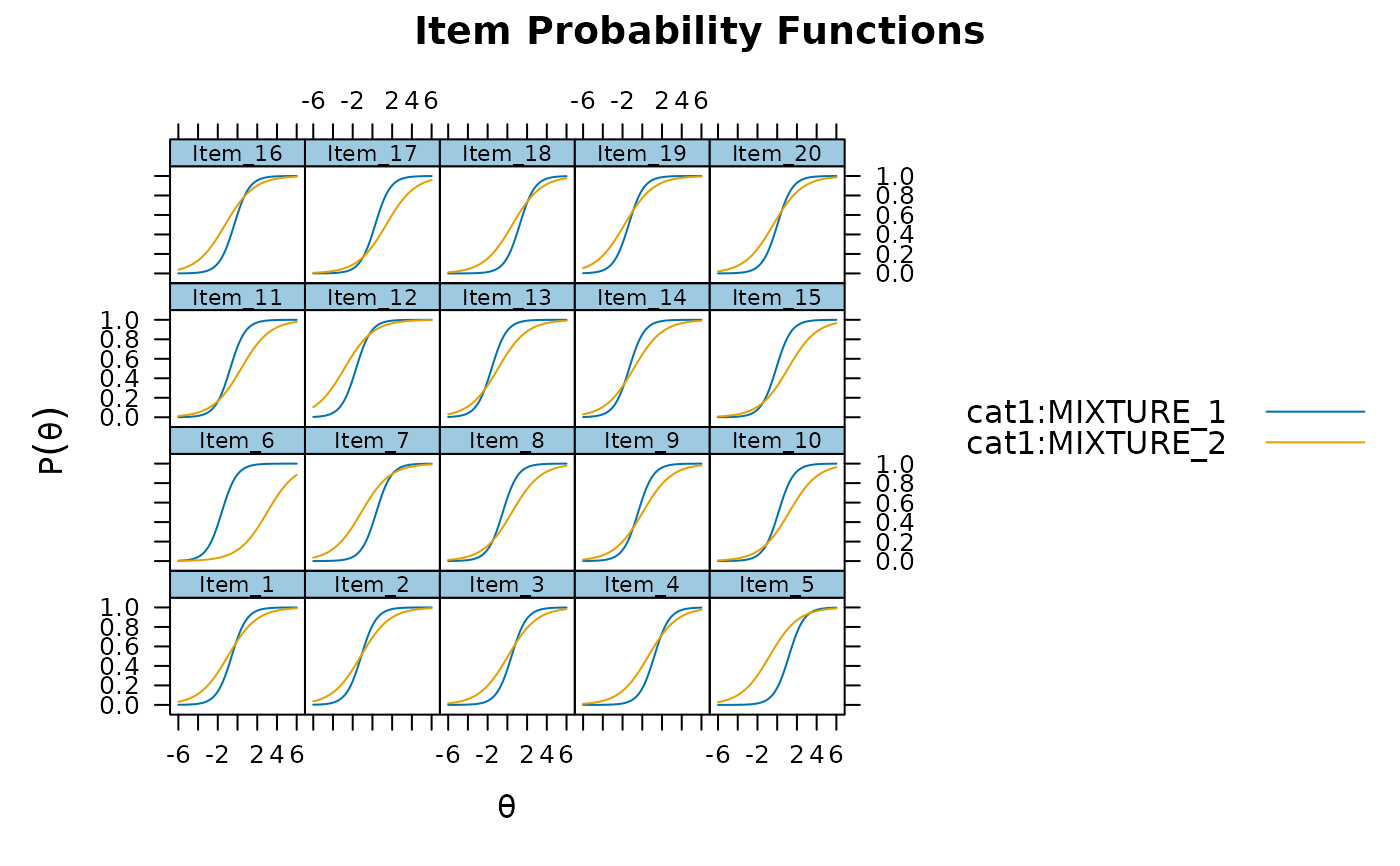itemplot(mod_mix, 1, type = 'info')
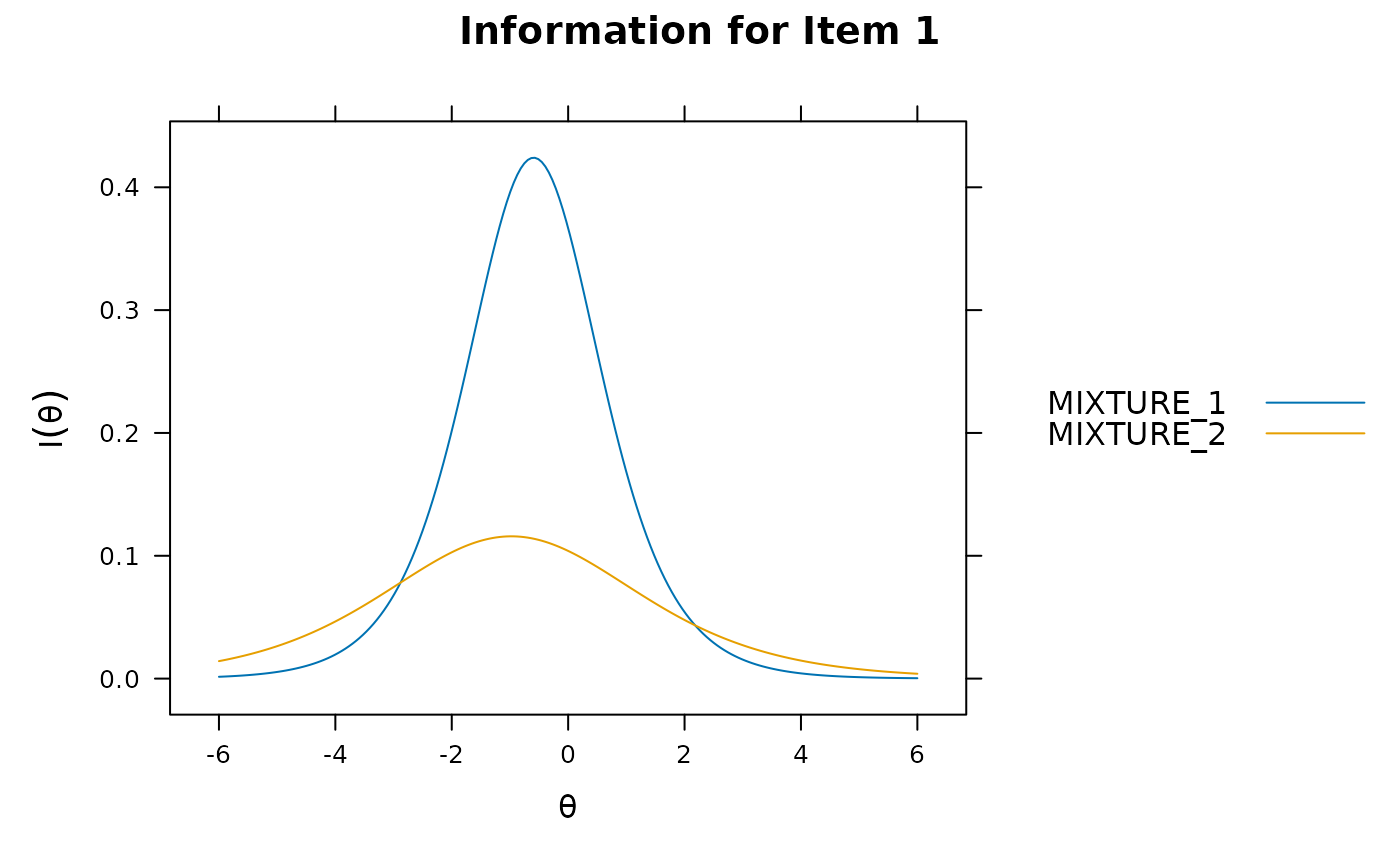head(fscores(mod_mix)) # theta estimates
#> Class_1
#> [1,] -0.3609178
#> [2,] -1.6950807
#> [3,] -0.8217168
#> [4,] 0.8090483
#> [5,] 0.7936363
#> [6,] 0.2286020
head(fscores(mod_mix, method = 'classify')) # classification probability
#> CLASS_1 CLASS_2
#> [1,] 0.04826707 0.9517329
#> [2,] 0.74223456 0.2577654
#> [3,] 0.02496631 0.9750337
#> [4,] 0.02929597 0.9707040
#> [5,] 0.07220958 0.9277904
#> [6,] 0.42428417 0.5757158
itemfit(mod_mix)
#> item S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
#> 1 Item_1 30.498 12 0.032 0.002
#> 2 Item_2 36.271 12 0.037 0.000
#> 3 Item_3 15.756 12 0.014 0.203
#> 4 Item_4 9.334 11 0.000 0.591
#> 5 Item_5 21.638 12 0.023 0.042
#> 6 Item_6 26.071 13 0.026 0.017
#> 7 Item_7 8.624 12 0.000 0.735
#> 8 Item_8 16.652 12 0.016 0.163
#> 9 Item_9 22.772 12 0.024 0.030
#> 10 Item_10 14.622 12 0.012 0.263
#> 11 Item_11 7.357 12 0.000 0.833
#> 12 Item_12 14.964 12 0.013 0.243
#> 13 Item_13 10.222 12 0.000 0.597
#> 14 Item_14 17.414 13 0.015 0.181
#> 15 Item_15 9.436 12 0.000 0.665
#> 16 Item_16 11.408 12 0.000 0.494
#> 17 Item_17 16.483 12 0.016 0.170
#> 18 Item_18 11.717 11 0.007 0.385
#> 19 Item_19 11.425 12 0.000 0.493
#> 20 Item_20 15.291 12 0.014 0.226
# Mixture 2PL model
mod_mix2 <- multipleGroup(dat, 1, dentype = 'mixture-2', GenRandomPars = TRUE)
anova(mod_mix, mod_mix2)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod_mix 34628.19 34720.06 34713.30 34856.65 -17271.09
#> mod_mix2 34655.23 34828.29 34815.56 35085.60 -17246.62 48.957 38 0.11
coef(mod_mix2, simplify=TRUE)
#> $MIXTURE_1
#> $items
#> a1 d g u
#> Item_1 0.517 0.672 0 1
#> Item_2 0.516 0.826 0 1
#> Item_3 0.533 -0.012 0 1
#> Item_4 0.387 -0.363 0 1
#> Item_5 0.452 0.551 0 1
#> Item_6 0.727 -1.905 0 1
#> Item_7 1.032 0.879 0 1
#> Item_8 0.744 -0.275 0 1
#> Item_9 0.900 0.037 0 1
#> Item_10 0.709 -0.777 0 1
#> Item_11 0.538 -0.190 0 1
#> Item_12 0.915 2.079 0 1
#> Item_13 0.729 0.690 0 1
#> Item_14 1.183 0.722 0 1
#> Item_15 0.812 -0.717 0 1
#> Item_16 0.582 0.843 0 1
#> Item_17 0.791 -0.953 0 1
#> Item_18 0.657 -0.290 0 1
#> Item_19 0.498 1.222 0 1
#> Item_20 0.468 0.304 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#> $class_proportion
#> pi
#> 0.349
#>
#>
#> $MIXTURE_2
#> $items
#> a1 d g u
#> Item_1 1.118 0.710 0 1
#> Item_2 1.216 1.405 0 1
#> Item_3 1.244 -0.565 0 1
#> Item_4 1.684 -1.826 0 1
#> Item_5 1.669 -1.800 0 1
#> Item_6 1.473 2.151 0 1
#> Item_7 1.143 -0.510 0 1
#> Item_8 1.244 0.574 0 1
#> Item_9 1.272 0.507 0 1
#> Item_10 1.188 -0.183 0 1
#> Item_11 1.465 0.980 0 1
#> Item_12 1.403 2.208 0 1
#> Item_13 1.388 2.110 0 1
#> Item_14 1.062 1.599 0 1
#> Item_15 1.311 0.112 0 1
#> Item_16 1.191 0.410 0 1
#> Item_17 1.381 -0.387 0 1
#> Item_18 1.500 -1.798 0 1
#> Item_19 1.624 1.955 0 1
#> Item_20 1.353 -0.060 0 1
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#> $class_proportion
#> pi
#> 0.651
#>
#>
itemfit(mod_mix2)
#> item S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
#> 1 Item_1 21.271 12 0.023 0.047
#> 2 Item_2 44.619 13 0.040 0.000
#> 3 Item_3 14.259 12 0.011 0.284
#> 4 Item_4 6.550 11 0.000 0.834
#> 5 Item_5 20.639 12 0.022 0.056
#> 6 Item_6 27.956 13 0.028 0.009
#> 7 Item_7 8.628 12 0.000 0.734
#> 8 Item_8 16.261 12 0.015 0.180
#> 9 Item_9 21.304 12 0.023 0.046
#> 10 Item_10 11.460 12 0.000 0.490
#> 11 Item_11 7.091 12 0.000 0.852
#> 12 Item_12 13.838 12 0.010 0.311
#> 13 Item_13 10.444 12 0.000 0.577
#> 14 Item_14 15.704 13 0.012 0.265
#> 15 Item_15 9.439 12 0.000 0.665
#> 16 Item_16 10.128 12 0.000 0.605
#> 17 Item_17 17.474 12 0.017 0.133
#> 18 Item_18 11.833 11 0.007 0.376
#> 19 Item_19 8.071 11 0.000 0.707
#> 20 Item_20 14.542 12 0.012 0.267
# Compare to single group
mod <- mirt(dat)
anova(mod, mod_mix2)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod 35276.70 35362.16 35355.88 35489.23 -17598.35
#> mod_mix2 34655.23 34828.29 34815.56 35085.60 -17246.62 703.474 41 0
########################################
# Zero-inflated 2PL IRT model (Wall, Park, and Moustaki, 2015)
n <- 1000
nitems <- 20
a <- rep(2, nitems)
d <- rep(c(-2,-1,0,1,2), each=nitems/5)
zi_p <- 0.2 # Proportion of people in zero class
theta <- rnorm(n, 0, 1)
zeros <- matrix(0, n*zi_p, nitems)
nonzeros <- simdata(a, d, n*(1-zi_p), itemtype = '2PL',
Theta = as.matrix(theta[1:(n*(1-zi_p))]))
data <- rbind(nonzeros, zeros)
# define class with extreme theta but fixed item parameters
zi2PL <- "F = 1-20
START [MIXTURE_1] = (GROUP, MEAN_1, -100), (GROUP, COV_11, .00001),
(1-20, a1, 1.0), (1-20, d, 0)
FIXED [MIXTURE_1] = (GROUP, MEAN_1), (GROUP, COV_11),
(1-20, a1), (1-20, d)"
# define custom Theta integration grid that contains extreme theta + normal grid
technical <- list(customTheta = matrix(c(-100, seq(-6,6,length.out=61))))
# fit ZIM-IRT
zi2PL.fit <- multipleGroup(data, zi2PL, dentype = 'mixture-2', technical=technical)
coef(zi2PL.fit, simplify=TRUE)
#> $MIXTURE_1
#> $items
#> a1 d g u
#> Item_1 1 0 0 1
#> Item_2 1 0 0 1
#> Item_3 1 0 0 1
#> Item_4 1 0 0 1
#> Item_5 1 0 0 1
#> Item_6 1 0 0 1
#> Item_7 1 0 0 1
#> Item_8 1 0 0 1
#> Item_9 1 0 0 1
#> Item_10 1 0 0 1
#> Item_11 1 0 0 1
#> Item_12 1 0 0 1
#> Item_13 1 0 0 1
#> Item_14 1 0 0 1
#> Item_15 1 0 0 1
#> Item_16 1 0 0 1
#> Item_17 1 0 0 1
#> Item_18 1 0 0 1
#> Item_19 1 0 0 1
#> Item_20 1 0 0 1
#>
#> $means
#> F
#> -100
#>
#> $cov
#> F
#> F 0
#>
#> $class_proportion
#> pi
#> 0.209
#>
#>
#> $MIXTURE_2
#> $items
#> a1 d g u
#> Item_1 1.867 -2.089 0 1
#> Item_2 1.998 -1.979 0 1
#> Item_3 1.954 -1.932 0 1
#> Item_4 1.595 -1.841 0 1
#> Item_5 1.922 -0.986 0 1
#> Item_6 1.924 -0.926 0 1
#> Item_7 2.045 -1.209 0 1
#> Item_8 2.069 -1.005 0 1
#> Item_9 1.782 0.101 0 1
#> Item_10 1.942 0.195 0 1
#> Item_11 2.080 0.039 0 1
#> Item_12 1.956 0.039 0 1
#> Item_13 1.540 0.835 0 1
#> Item_14 2.047 1.092 0 1
#> Item_15 1.956 0.973 0 1
#> Item_16 1.807 1.026 0 1
#> Item_17 2.084 2.069 0 1
#> Item_18 1.917 2.153 0 1
#> Item_19 1.464 1.735 0 1
#> Item_20 1.739 1.920 0 1
#>
#> $means
#> F
#> 0
#>
#> $cov
#> F
#> F 1
#>
#> $class_proportion
#> pi
#> 0.791
#>
#>
# classification estimates
pi_hat <- fscores(zi2PL.fit, method = 'classify')
head(pi_hat)
#> CLASS_1 CLASS_2
#> [1,] 8.544142e-180 1
#> [2,] 2.267724e-14 1
#> [3,] 2.122840e-178 1
#> [4,] 4.509158e-210 1
#> [5,] 1.130538e-13 1
#> [6,] 9.974115e-149 1
tail(pi_hat)
#> CLASS_1 CLASS_2
#> [995,] 0.9243758 0.07562418
#> [996,] 0.9243758 0.07562418
#> [997,] 0.9243758 0.07562418
#> [998,] 0.9243758 0.07562418
#> [999,] 0.9243758 0.07562418
#> [1000,] 0.9243758 0.07562418
# EAP estimates (not useful for zip class)
fs <- fscores(zi2PL.fit)
head(fs)
#> Class_1
#> [1,] 0.262140462
#> [2,] -1.762463343
#> [3,] 0.285984614
#> [4,] 0.562650718
#> [5,] -1.669323391
#> [6,] 0.005541674
tail(fs)
#> Class_1
#> [995,] -92.59647
#> [996,] -92.59647
#> [997,] -92.59647
#> [998,] -92.59647
#> [999,] -92.59647
#> [1000,] -92.59647
########################################
# Zero-inflated graded response model (Magnus and Garnier-Villarreal, 2022)
n <- 1000
nitems <- 20
a <- matrix(rlnorm(20,.2,.3))
# for the graded model, ensure that there is enough space between the intercepts,
# otherwise closer categories will not be selected often (minimum distance of 0.3 here)
diffs <- t(apply(matrix(runif(20*4, .3, 1), 20), 1, cumsum))
diffs <- -(diffs - rowMeans(diffs))
d <- diffs + rnorm(20)
zi_p <- 0.2 # Proportion of people in zero/lowest category class
theta <- rnorm(n, 0, 1)
zeros <- matrix(0, n*zi_p, nitems)
nonzeros <- simdata(a, d, n*(1-zi_p), itemtype = 'graded',
Theta = as.matrix(theta[1:(n*(1-zi_p))]))
data <- rbind(nonzeros, zeros)
# intercepts will be labelled as d1 through d4
apply(data, 2, table)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Item_6 Item_7 Item_8 Item_9 Item_10
#> 0 474 276 431 384 763 354 420 379 342 610
#> 1 128 61 107 26 69 99 140 137 116 114
#> 2 62 105 112 54 45 58 120 136 165 98
#> 3 89 135 159 87 37 135 118 70 68 34
#> 4 247 423 191 449 86 354 202 278 309 144
#> Item_11 Item_12 Item_13 Item_14 Item_15 Item_16 Item_17 Item_18 Item_19
#> 0 393 756 668 605 463 321 683 664 406
#> 1 115 114 75 104 74 55 65 46 99
#> 2 54 62 55 113 119 123 58 46 66
#> 3 134 33 66 81 89 130 42 57 67
#> 4 304 35 136 97 255 371 152 187 362
#> Item_20
#> 0 588
#> 1 103
#> 2 85
#> 3 50
#> 4 174
# ignoring zero inflation (bad idea)
modGRM <- mirt(data)
#> Warning: EM cycles terminated after 500 iterations.
coef(modGRM, simplify=TRUE)
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 2.540 -0.222 -1.106 -1.527 -2.166
#> Item_2 2.284 1.418 0.791 -0.010 -0.848
#> Item_3 1.771 0.167 -0.479 -1.108 -2.132
#> Item_4 3.367 0.392 0.141 -0.330 -1.021
#> Item_5 3.450 -2.805 -3.524 -4.104 -4.690
#> Item_6 2.003 0.715 0.013 -0.347 -1.145
#> Item_7 2.375 0.182 -0.781 -1.545 -2.404
#> Item_8 2.286 0.516 -0.465 -1.336 -1.795
#> Item_9 2.768 0.837 -0.152 -1.318 -1.801
#> Item_10 2.910 -1.290 -2.154 -3.033 -3.397
#> Item_11 2.681 0.382 -0.484 -0.857 -1.792
#> Item_12 1.734 -1.721 -2.648 -3.462 -4.224
#> Item_13 2.042 -1.306 -1.802 -2.209 -2.804
#> Item_14 1.914 -0.871 -1.516 -2.346 -3.184
#> Item_15 4.247 -0.504 -1.187 -2.250 -3.114
#> Item_16 2.628 1.020 0.501 -0.428 -1.305
#> Item_17 2.522 -1.628 -2.114 -2.605 -3.007
#> Item_18 2.547 -1.507 -1.835 -2.189 -2.675
#> Item_19 1.906 0.340 -0.291 -0.677 -1.065
#> Item_20 2.287 -0.906 -1.572 -2.181 -2.606
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
# Define class with extreme theta but fixed item parameters
# For GRM in zero-inflated class the intercept values are arbitrary
# as the model forces the responses all into the first category (hence,
# spacing arbitrarily set to 1)
ziGRM <- "F = 1-20
START [MIXTURE_1] = (GROUP, MEAN_1, -100), (GROUP, COV_11, .00001),
(1-20, a1, 1.0),
(1-20, d1, 2), (1-20, d2, 1), (1-20, d3, 0), (1-20, d4, -1)
FIXED [MIXTURE_1] = (GROUP, MEAN_1), (GROUP, COV_11),
(1-20, a1),
(1-20, d1), (1-20, d2), (1-20, d3), (1-20, d4)"
# define custom Theta integration grid that contains extreme theta + normal grid
technical <- list(customTheta = matrix(c(-100, seq(-6,6,length.out=61))))
# fit zero-inflated GRM
ziGRM.fit <- multipleGroup(data, ziGRM, dentype = 'mixture-2', technical=technical)
coef(ziGRM.fit, simplify=TRUE)
#> $MIXTURE_1
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1 2 1 0 -1
#> Item_2 1 2 1 0 -1
#> Item_3 1 2 1 0 -1
#> Item_4 1 2 1 0 -1
#> Item_5 1 2 1 0 -1
#> Item_6 1 2 1 0 -1
#> Item_7 1 2 1 0 -1
#> Item_8 1 2 1 0 -1
#> Item_9 1 2 1 0 -1
#> Item_10 1 2 1 0 -1
#> Item_11 1 2 1 0 -1
#> Item_12 1 2 1 0 -1
#> Item_13 1 2 1 0 -1
#> Item_14 1 2 1 0 -1
#> Item_15 1 2 1 0 -1
#> Item_16 1 2 1 0 -1
#> Item_17 1 2 1 0 -1
#> Item_18 1 2 1 0 -1
#> Item_19 1 2 1 0 -1
#> Item_20 1 2 1 0 -1
#>
#> $means
#> F
#> -100
#>
#> $cov
#> F
#> F 0
#>
#> $class_proportion
#> pi
#> 0.2
#>
#>
#> $MIXTURE_2
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1.287 0.857 -0.022 -0.438 -1.068
#> Item_2 0.764 2.477 1.751 0.932 0.124
#> Item_3 0.695 0.975 0.325 -0.293 -1.284
#> Item_4 1.711 1.782 1.532 1.064 0.381
#> Item_5 1.928 -1.382 -2.106 -2.689 -3.276
#> Item_6 0.751 1.601 0.875 0.518 -0.255
#> Item_7 1.137 1.198 0.242 -0.506 -1.343
#> Item_8 1.030 1.498 0.515 -0.332 -0.778
#> Item_9 1.307 1.994 0.998 -0.138 -0.604
#> Item_10 1.583 -0.062 -0.930 -1.809 -2.171
#> Item_11 1.308 1.508 0.644 0.276 -0.636
#> Item_12 0.886 -0.954 -1.873 -2.677 -3.431
#> Item_13 1.048 -0.420 -0.912 -1.315 -1.903
#> Item_14 0.946 -0.030 -0.668 -1.485 -2.310
#> Item_15 2.338 1.299 0.604 -0.475 -1.353
#> Item_16 1.154 2.119 1.582 0.664 -0.180
#> Item_17 1.363 -0.559 -1.046 -1.536 -1.937
#> Item_18 1.359 -0.428 -0.755 -1.108 -1.591
#> Item_19 0.725 1.173 0.539 0.161 -0.216
#> Item_20 1.179 0.077 -0.586 -1.190 -1.609
#>
#> $means
#> F
#> 0
#>
#> $cov
#> F
#> F 1
#>
#> $class_proportion
#> pi
#> 0.8
#>
#>
# classification estimates
pi_hat <- fscores(ziGRM.fit, method = 'classify')
head(pi_hat)
#> CLASS_1 CLASS_2
#> [1,] 7.494632e-176 1
#> [2,] 9.061521e-303 1
#> [3,] 8.797228e-303 1
#> [4,] 8.991330e-293 1
#> [5,] 2.992170e-231 1
#> [6,] 1.967058e-82 1
tail(pi_hat)
#> CLASS_1 CLASS_2
#> [995,] 0.9982456 0.001754397
#> [996,] 0.9982456 0.001754397
#> [997,] 0.9982456 0.001754397
#> [998,] 0.9982456 0.001754397
#> [999,] 0.9982456 0.001754397
#> [1000,] 0.9982456 0.001754397
# EAP estimates (not useful for zip class)
fs <- fscores(ziGRM.fit)
head(fs)
#> Class_1
#> [1,] -0.5412083
#> [2,] 0.8572725
#> [3,] 1.5055425
#> [4,] 1.1937281
#> [5,] 0.2213622
#> [6,] -1.4092124
tail(fs)
#> Class_1
#> [995,] -99.82944
#> [996,] -99.82944
#> [997,] -99.82944
#> [998,] -99.82944
#> [999,] -99.82944
#> [1000,] -99.82944
# }