Function performs various omnibus differential item (DIF), bundle (DBF), and test (DTF)
functioning procedures on an object
estimated with multipleGroup(). The compensatory and non-compensatory statistics provided
are described in Chalmers (2018), which generally can be interpreted as IRT generalizations
of the SIBTEST and CSIBTEST statistics. For hypothesis tests, these measures
require the ACOV matrix to be computed in the
fitted multiple-group model (otherwise, sets of plausible draws from the posterior are explicitly
required).
Usage
DRF(
mod,
draws = NULL,
focal_items = 1L:extract.mirt(mod, "nitems"),
param_set = NULL,
den.type = "marginal",
best_fitting = FALSE,
CI = 0.95,
npts = 1000,
quadpts = NULL,
theta_lim = c(-6, 6),
Theta_nodes = NULL,
plot = FALSE,
DIF = FALSE,
DIF.cats = FALSE,
groups2test = "all",
pairwise = FALSE,
simplify = TRUE,
p.adjust = "none",
par.strip.text = list(cex = 0.7),
par.settings = list(strip.background = list(col = "#9ECAE1"), strip.border = list(col =
"black")),
auto.key = list(space = "right", points = FALSE, lines = TRUE),
verbose = TRUE,
...
)Arguments
- mod
a multipleGroup object which estimated only 2 groups
- draws
a number indicating how many draws to take to form a suitable multiple imputation or bootstrap estimate of the expected test scores (100 or more). If
boot = FALSE, requires an estimated parameter information matrix. Returns a list containing the bootstrap/imputation distribution and null hypothesis test for the sDRF statistics- focal_items
a character/numeric vector indicating which items to include in the DRF tests. The default uses all of the items (note that including anchors in the focal items has no effect because they are exactly equal across groups). Selecting fewer items will result in tests of 'differential bundle functioning'
- param_set
an N x p matrix of parameter values drawn from the posterior (e.g., using the parametric sampling approach, bootstrap, of MCMC). If supplied, then these will be used to compute the DRF measures. Can be much more efficient to pre-compute these values if DIF, DBF, or DTF are being evaluated within the same model (especially when using the bootstrap method). See
draw_parameters- den.type
character specifying how the density of the latent traits is computed. Default is
'marginal'to include the proportional information from both groups,'focal'for just the focal group, and'reference'for the reference group- best_fitting
logical; use the best fitting parametric distribution (Gaussian by default) that was used at the time of model estimation? This will result in much fast computations, however the results are more dependent upon the underlying modelling assumptions. Default is FALSE, which uses the empirical histogram approach
- CI
range of confidence interval when using draws input
- npts
number of points to use for plotting. Default is 1000
- quadpts
number of quadrature nodes to use when constructing DRF statistics. Default is extracted from the input model object
- theta_lim
lower and upper limits of the latent trait (theta) to be evaluated, and is used in conjunction with
quadptsandnpts- Theta_nodes
an optional matrix of Theta values to be evaluated in the draws for the sDRF statistics. However, these values are not averaged across, and instead give the bootstrap confidence intervals at the respective Theta nodes. Useful when following up a large sDRF or uDRF statistic, for example, to determine where the difference between the test curves are large (while still accounting for sampling variability). Returns a matrix with observed variability
- plot
logical; plot the 'sDRF' functions for the evaluated sDBF or sDTF values across the integration grid or, if
DIF = TRUE, the selected items as a faceted plot of individual items? If plausible parameter sets were obtained/supplied then imputed confidence intervals will be included- DIF
logical; return a list of item-level imputation properties using the DRF statistics? These can generally be used as a DIF detection method and as a graphical display for understanding DIF within each item
- DIF.cats
logical; same as
DIF = TRUE, however computations will be performed on each item category probability functions rather than the score functions. Only useful for understanding DIF in polytomous items- groups2test
when more than 2 groups are being investigated which two groups should be used in the effect size comparisons?
- pairwise
logical; perform pairwise computations when the applying to multi-group settings
- simplify
logical; attempt to simplify the output rather than returning larger lists?
- p.adjust
string to be passed to the
p.adjustfunction to adjust p-values. Adjustments are located in theadj_pvalselement in the returned list. Only applicable whenDIF = TRUE- par.strip.text
plotting argument passed to
lattice- par.settings
plotting argument passed to
lattice- auto.key
plotting argument passed to
lattice- verbose
logical; include additional information in the console?
- ...
additional arguments to be passed to
lattice
Details
The effect sizes estimates by the DRF function are $$sDRF = \int [S(C|\bm{\Psi}^{(R)},\theta) S(C|\bm{\Psi}^{(F)},\theta)] f(\theta)d\theta,$$ $$uDRF = \int |S(C|\bm{\Psi}^{(R)},\theta) S(C|\bm{\Psi}^{(F)},\theta)| f(\theta)d\theta,$$ and $$dDRF = \sqrt{\int [S(C|\bm{\Psi}^{(R)},\theta) S(C|\bm{\Psi}^{(F)},\theta)]^2 f(\theta)d\theta}$$ where \(S(.)\) are the scoring equations used to evaluate the model-implied difference between the focal and reference group. The \(f(\theta)\) terms can either be estimated from the posterior via an empirical histogram approach (default), or can use the best fitting prior distribution that is obtain post-convergence (default is a Guassian distribution). Note that, in comparison to Chalmers (2018), the focal group is the leftmost scoring function while the reference group is the rightmost scoring function. This is largely to keep consistent with similar effect size statistics, such as SIBTEST, DFIT, Wainer's measures of impact, etc, which in general can be seen as special-case estimators of this family.
References
Chalmers, R. P. (2018). Model-Based Measures for Detecting and Quantifying Response Bias. Psychometrika, 83(3), 696-732. doi:10.1007/s11336-018-9626-9
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
# \donttest{
set.seed(1234)
n <- 30
N <- 500
# only first 5 items as anchors
model <- 'F = 1-30
CONSTRAINB = (1-5, a1), (1-5, d)'
a <- matrix(1, n)
d <- matrix(rnorm(n), n)
group <- c(rep('Group_1', N), rep('Group_2', N))
## -------------
# groups completely equal
dat1 <- simdata(a, d, N, itemtype = 'dich')
dat2 <- simdata(a, d, N, itemtype = 'dich')
dat <- rbind(dat1, dat2)
mod <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
plot(mod)
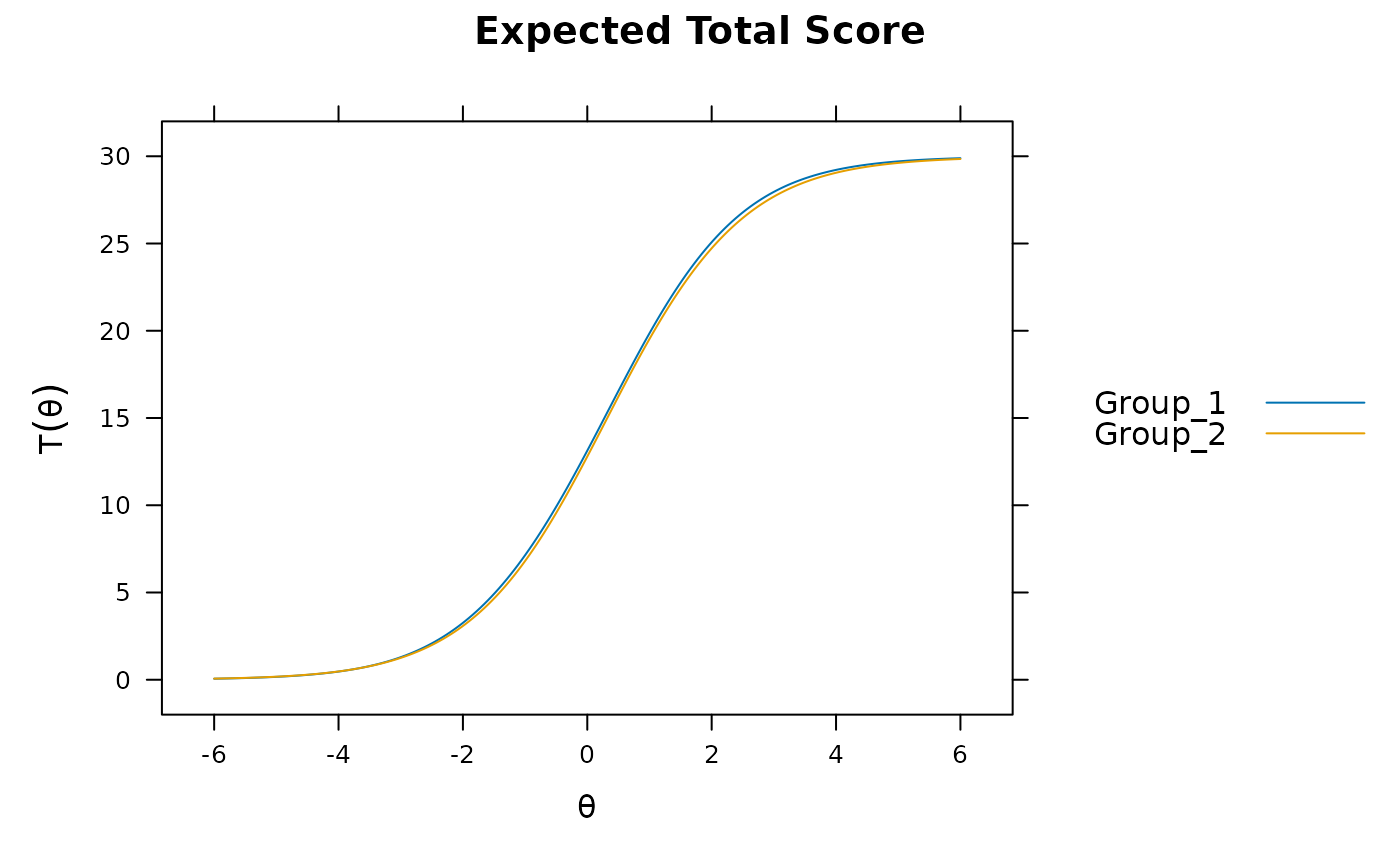 plot(mod, which.items = 6:10) #DBF
plot(mod, which.items = 6:10) #DBF
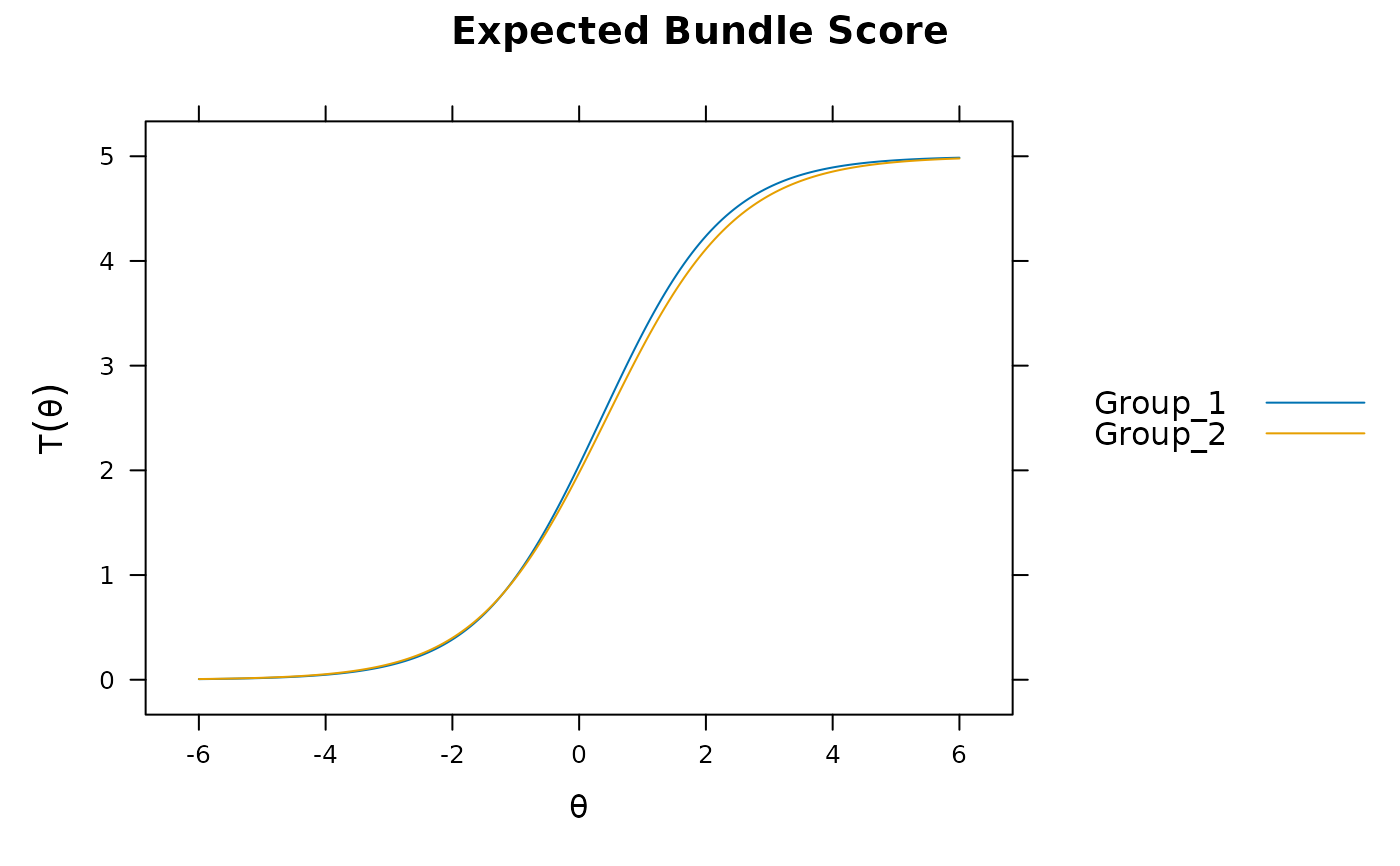 plot(mod, type = 'itemscore')
plot(mod, type = 'itemscore')
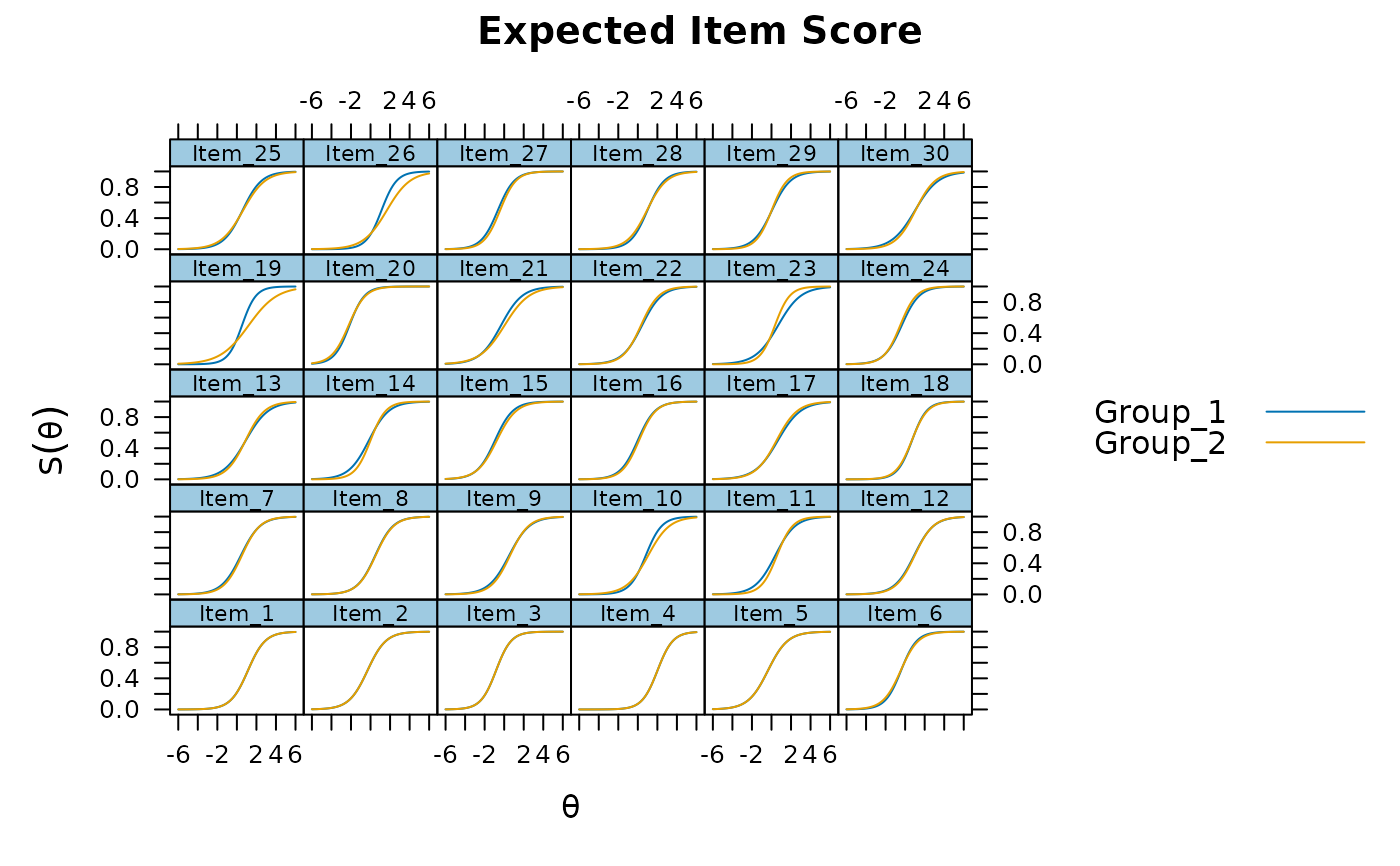 plot(mod, type = 'itemscore', which.items = 10:15)
plot(mod, type = 'itemscore', which.items = 10:15)
 # empirical histogram approach
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.326 0.326 0.328
DRF(mod, focal_items = 6:10) #DBF
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 5 -0.069 0.071 0.084
DRF(mod, DIF=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 0.016 0.018
#> 7 Group_1,Group_2 Item_7 -0.026 0.026 0.028
#> 8 Group_1,Group_2 Item_8 -0.008 0.008 0.008
#> 9 Group_1,Group_2 Item_9 -0.026 0.026 0.028
#> 10 Group_1,Group_2 Item_10 -0.010 0.036 0.044
#> 11 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 12 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 13 Group_1,Group_2 Item_13 -0.015 0.022 0.025
#> 14 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 15 Group_1,Group_2 Item_15 -0.045 0.045 0.047
#> 16 Group_1,Group_2 Item_16 -0.030 0.030 0.032
#> 17 Group_1,Group_2 Item_17 0.018 0.019 0.023
#> 18 Group_1,Group_2 Item_18 0.011 0.013 0.014
#> 19 Group_1,Group_2 Item_19 -0.045 0.094 0.117
#> 20 Group_1,Group_2 Item_20 -0.008 0.010 0.010
#> 21 Group_1,Group_2 Item_21 -0.070 0.070 0.073
#> 22 Group_1,Group_2 Item_22 0.017 0.020 0.024
#> 23 Group_1,Group_2 Item_23 0.036 0.064 0.078
#> 24 Group_1,Group_2 Item_24 0.040 0.040 0.042
#> 25 Group_1,Group_2 Item_25 0.002 0.018 0.021
#> 26 Group_1,Group_2 Item_26 -0.019 0.047 0.065
#> 27 Group_1,Group_2 Item_27 -0.049 0.049 0.052
#> 28 Group_1,Group_2 Item_28 0.027 0.029 0.031
#> 29 Group_1,Group_2 Item_29 0.007 0.025 0.028
#> 30 Group_1,Group_2 Item_30 -0.029 0.031 0.033
DRF(mod, DIF=TRUE, focal_items = 10:15)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_10 -0.010 0.036 0.044
#> 2 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 3 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 4 Group_1,Group_2 Item_13 -0.015 0.022 0.025
#> 5 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 6 Group_1,Group_2 Item_15 -0.045 0.045 0.047
# Best-fitting Gaussian distributions
DRF(mod, best_fitting=TRUE)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.326 0.326 0.328
DRF(mod, focal_items = 6:10, best_fitting=TRUE) #DBF
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 5 -0.069 0.071 0.084
DRF(mod, DIF=TRUE, best_fitting=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 0.016 0.018
#> 7 Group_1,Group_2 Item_7 -0.026 0.026 0.028
#> 8 Group_1,Group_2 Item_8 -0.008 0.008 0.008
#> 9 Group_1,Group_2 Item_9 -0.026 0.026 0.028
#> 10 Group_1,Group_2 Item_10 -0.010 0.036 0.045
#> 11 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 12 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 13 Group_1,Group_2 Item_13 -0.015 0.023 0.025
#> 14 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 15 Group_1,Group_2 Item_15 -0.045 0.045 0.047
#> 16 Group_1,Group_2 Item_16 -0.030 0.030 0.032
#> 17 Group_1,Group_2 Item_17 0.018 0.019 0.023
#> 18 Group_1,Group_2 Item_18 0.011 0.013 0.014
#> 19 Group_1,Group_2 Item_19 -0.045 0.094 0.118
#> 20 Group_1,Group_2 Item_20 -0.008 0.010 0.010
#> 21 Group_1,Group_2 Item_21 -0.070 0.070 0.073
#> 22 Group_1,Group_2 Item_22 0.017 0.020 0.024
#> 23 Group_1,Group_2 Item_23 0.036 0.064 0.078
#> 24 Group_1,Group_2 Item_24 0.040 0.040 0.042
#> 25 Group_1,Group_2 Item_25 0.002 0.019 0.021
#> 26 Group_1,Group_2 Item_26 -0.019 0.047 0.065
#> 27 Group_1,Group_2 Item_27 -0.049 0.049 0.052
#> 28 Group_1,Group_2 Item_28 0.027 0.029 0.031
#> 29 Group_1,Group_2 Item_29 0.007 0.025 0.028
#> 30 Group_1,Group_2 Item_30 -0.029 0.031 0.033
DRF(mod, DIF=TRUE, focal_items = 10:15, best_fitting=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_10 -0.010 0.036 0.045
#> 2 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 3 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 4 Group_1,Group_2 Item_13 -0.015 0.023 0.025
#> 5 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 6 Group_1,Group_2 Item_15 -0.045 0.045 0.047
DRF(mod, plot = TRUE)
# empirical histogram approach
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.326 0.326 0.328
DRF(mod, focal_items = 6:10) #DBF
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 5 -0.069 0.071 0.084
DRF(mod, DIF=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 0.016 0.018
#> 7 Group_1,Group_2 Item_7 -0.026 0.026 0.028
#> 8 Group_1,Group_2 Item_8 -0.008 0.008 0.008
#> 9 Group_1,Group_2 Item_9 -0.026 0.026 0.028
#> 10 Group_1,Group_2 Item_10 -0.010 0.036 0.044
#> 11 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 12 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 13 Group_1,Group_2 Item_13 -0.015 0.022 0.025
#> 14 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 15 Group_1,Group_2 Item_15 -0.045 0.045 0.047
#> 16 Group_1,Group_2 Item_16 -0.030 0.030 0.032
#> 17 Group_1,Group_2 Item_17 0.018 0.019 0.023
#> 18 Group_1,Group_2 Item_18 0.011 0.013 0.014
#> 19 Group_1,Group_2 Item_19 -0.045 0.094 0.117
#> 20 Group_1,Group_2 Item_20 -0.008 0.010 0.010
#> 21 Group_1,Group_2 Item_21 -0.070 0.070 0.073
#> 22 Group_1,Group_2 Item_22 0.017 0.020 0.024
#> 23 Group_1,Group_2 Item_23 0.036 0.064 0.078
#> 24 Group_1,Group_2 Item_24 0.040 0.040 0.042
#> 25 Group_1,Group_2 Item_25 0.002 0.018 0.021
#> 26 Group_1,Group_2 Item_26 -0.019 0.047 0.065
#> 27 Group_1,Group_2 Item_27 -0.049 0.049 0.052
#> 28 Group_1,Group_2 Item_28 0.027 0.029 0.031
#> 29 Group_1,Group_2 Item_29 0.007 0.025 0.028
#> 30 Group_1,Group_2 Item_30 -0.029 0.031 0.033
DRF(mod, DIF=TRUE, focal_items = 10:15)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_10 -0.010 0.036 0.044
#> 2 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 3 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 4 Group_1,Group_2 Item_13 -0.015 0.022 0.025
#> 5 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 6 Group_1,Group_2 Item_15 -0.045 0.045 0.047
# Best-fitting Gaussian distributions
DRF(mod, best_fitting=TRUE)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.326 0.326 0.328
DRF(mod, focal_items = 6:10, best_fitting=TRUE) #DBF
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 5 -0.069 0.071 0.084
DRF(mod, DIF=TRUE, best_fitting=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 0.016 0.018
#> 7 Group_1,Group_2 Item_7 -0.026 0.026 0.028
#> 8 Group_1,Group_2 Item_8 -0.008 0.008 0.008
#> 9 Group_1,Group_2 Item_9 -0.026 0.026 0.028
#> 10 Group_1,Group_2 Item_10 -0.010 0.036 0.045
#> 11 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 12 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 13 Group_1,Group_2 Item_13 -0.015 0.023 0.025
#> 14 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 15 Group_1,Group_2 Item_15 -0.045 0.045 0.047
#> 16 Group_1,Group_2 Item_16 -0.030 0.030 0.032
#> 17 Group_1,Group_2 Item_17 0.018 0.019 0.023
#> 18 Group_1,Group_2 Item_18 0.011 0.013 0.014
#> 19 Group_1,Group_2 Item_19 -0.045 0.094 0.118
#> 20 Group_1,Group_2 Item_20 -0.008 0.010 0.010
#> 21 Group_1,Group_2 Item_21 -0.070 0.070 0.073
#> 22 Group_1,Group_2 Item_22 0.017 0.020 0.024
#> 23 Group_1,Group_2 Item_23 0.036 0.064 0.078
#> 24 Group_1,Group_2 Item_24 0.040 0.040 0.042
#> 25 Group_1,Group_2 Item_25 0.002 0.019 0.021
#> 26 Group_1,Group_2 Item_26 -0.019 0.047 0.065
#> 27 Group_1,Group_2 Item_27 -0.049 0.049 0.052
#> 28 Group_1,Group_2 Item_28 0.027 0.029 0.031
#> 29 Group_1,Group_2 Item_29 0.007 0.025 0.028
#> 30 Group_1,Group_2 Item_30 -0.029 0.031 0.033
DRF(mod, DIF=TRUE, focal_items = 10:15, best_fitting=TRUE)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_10 -0.010 0.036 0.045
#> 2 Group_1,Group_2 Item_11 -0.056 0.059 0.065
#> 3 Group_1,Group_2 Item_12 -0.016 0.016 0.017
#> 4 Group_1,Group_2 Item_13 -0.015 0.023 0.025
#> 5 Group_1,Group_2 Item_14 -0.033 0.046 0.054
#> 6 Group_1,Group_2 Item_15 -0.045 0.045 0.047
DRF(mod, plot = TRUE)
 DRF(mod, focal_items = 6:10, plot = TRUE) #DBF
DRF(mod, focal_items = 6:10, plot = TRUE) #DBF
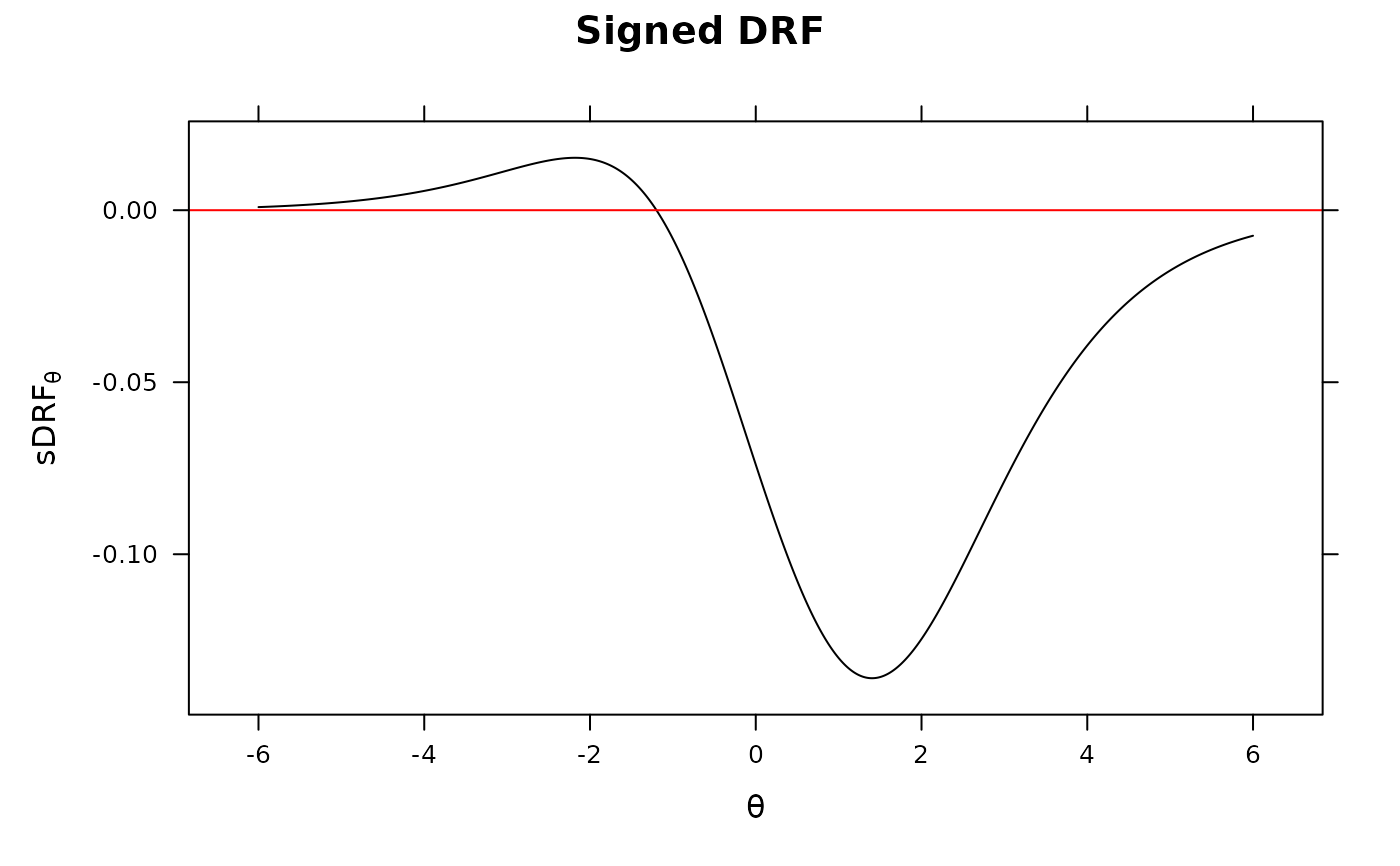 DRF(mod, DIF=TRUE, plot = TRUE)
DRF(mod, DIF=TRUE, plot = TRUE)
 DRF(mod, DIF=TRUE, focal_items = 10:15, plot = TRUE)
DRF(mod, DIF=TRUE, focal_items = 10:15, plot = TRUE)
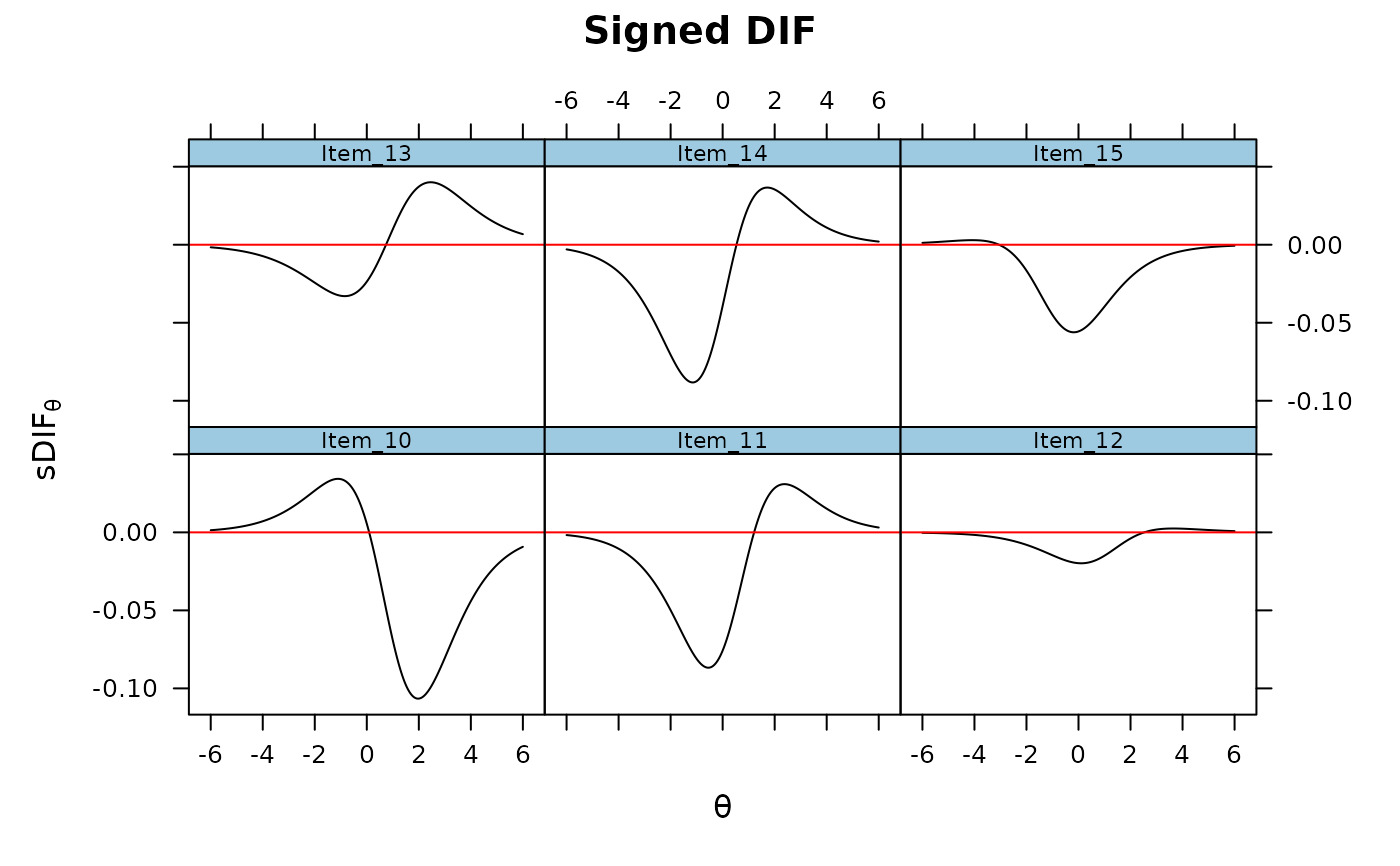 if(interactive()) mirtCluster()
DRF(mod, draws = 500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -0.957 0.360 0.983 1 0.321
#> uDRF Group_1,Group_2 30 0.326 0.102 0.957 2.644 2 0.267
#> dDRF Group_1,Group_2 30 0.328 0.125 1.044
DRF(mod, draws = 500, best_fitting=TRUE)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -0.977 0.339 0.939 1 0.333
#> uDRF Group_1,Group_2 30 0.326 0.095 0.977 2.614 2 0.271
#> dDRF Group_1,Group_2 30 0.328 0.108 1.086
DRF(mod, draws = 500, plot=TRUE)
if(interactive()) mirtCluster()
DRF(mod, draws = 500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -0.957 0.360 0.983 1 0.321
#> uDRF Group_1,Group_2 30 0.326 0.102 0.957 2.644 2 0.267
#> dDRF Group_1,Group_2 30 0.328 0.125 1.044
DRF(mod, draws = 500, best_fitting=TRUE)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -0.977 0.339 0.939 1 0.333
#> uDRF Group_1,Group_2 30 0.326 0.095 0.977 2.614 2 0.271
#> dDRF Group_1,Group_2 30 0.328 0.108 1.086
DRF(mod, draws = 500, plot=TRUE)
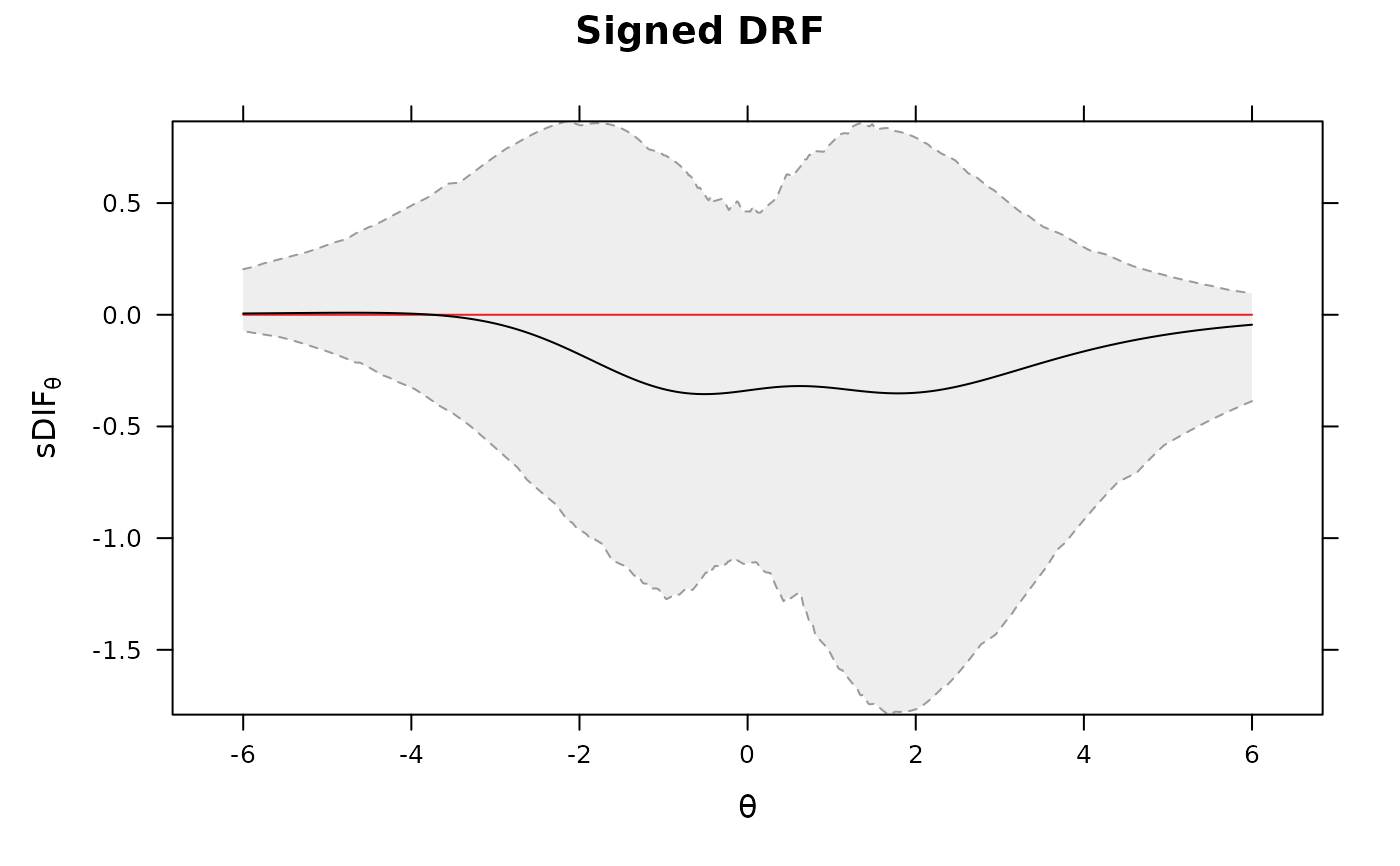 # pre-draw parameter set to save computations
# (more useful when using non-parametric bootstrap)
param_set <- draw_parameters(mod, draws = 500)
DRF(mod, focal_items = 6, param_set=param_set) #DIF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 1 0.000 -0.058 0.066 0 1 0.999
#> uDRF Group_1,Group_2 1 0.016 0.007 0.085 0.768 2 0.681
#> dDRF Group_1,Group_2 1 0.018 0.008 0.098
DRF(mod, DIF=TRUE, param_set=param_set) #DIF test
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 -0.058 0.066 0 1 0.999
#> 7 Group_1,Group_2 Item_7 -0.026 -0.087 0.040 0.653 1 0.419
#> 8 Group_1,Group_2 Item_8 -0.008 -0.060 0.058 0.066 1 0.798
#> 9 Group_1,Group_2 Item_9 -0.026 -0.091 0.031 0.649 1 0.421
#> 10 Group_1,Group_2 Item_10 -0.010 -0.072 0.048 0.101 1 0.751
#> 11 Group_1,Group_2 Item_11 -0.056 -0.116 0.003 3.557 1 0.059
#> 12 Group_1,Group_2 Item_12 -0.016 -0.074 0.038 0.305 1 0.581
#> 13 Group_1,Group_2 Item_13 -0.015 -0.075 0.041 0.234 1 0.629
#> 14 Group_1,Group_2 Item_14 -0.033 -0.096 0.027 1.029 1 0.31
#> 15 Group_1,Group_2 Item_15 -0.045 -0.103 0.012 2.479 1 0.115
#> 16 Group_1,Group_2 Item_16 -0.030 -0.098 0.036 0.883 1 0.348
#> 17 Group_1,Group_2 Item_17 0.018 -0.042 0.079 0.31 1 0.578
#> 18 Group_1,Group_2 Item_18 0.011 -0.051 0.072 0.125 1 0.723
#> 19 Group_1,Group_2 Item_19 -0.045 -0.103 0.011 2.293 1 0.13
#> 20 Group_1,Group_2 Item_20 -0.008 -0.045 0.034 0.159 1 0.69
#> 21 Group_1,Group_2 Item_21 -0.070 -0.133 -0.006 4.678 1 0.031
#> 22 Group_1,Group_2 Item_22 0.017 -0.048 0.071 0.312 1 0.576
#> 23 Group_1,Group_2 Item_23 0.036 -0.031 0.098 1.291 1 0.256
#> 24 Group_1,Group_2 Item_24 0.040 -0.021 0.097 1.787 1 0.181
#> 25 Group_1,Group_2 Item_25 0.002 -0.062 0.061 0.004 1 0.949
#> 26 Group_1,Group_2 Item_26 -0.019 -0.075 0.037 0.471 1 0.493
#> 27 Group_1,Group_2 Item_27 -0.049 -0.111 0.014 2.298 1 0.13
#> 28 Group_1,Group_2 Item_28 0.027 -0.036 0.090 0.681 1 0.409
#> 29 Group_1,Group_2 Item_29 0.007 -0.057 0.073 0.05 1 0.824
#> 30 Group_1,Group_2 Item_30 -0.029 -0.092 0.022 1.002 1 0.317
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.016 0.007 0.085 0.768 2 0.681
#> 7 Group_1,Group_2 Item_7 0.026 0.008 0.090 1.944 2 0.378
#> 8 Group_1,Group_2 Item_8 0.008 0.005 0.073 0.225 2 0.893
#> 9 Group_1,Group_2 Item_9 0.026 0.008 0.093 2.093 2 0.351
#> 10 Group_1,Group_2 Item_10 0.036 0.008 0.107 3.281 2 0.194
#> 11 Group_1,Group_2 Item_11 0.059 0.015 0.113 10.147 2 0.006
#> 12 Group_1,Group_2 Item_12 0.016 0.005 0.074 0.849 2 0.654
#> 13 Group_1,Group_2 Item_13 0.022 0.007 0.084 1.69 2 0.43
#> 14 Group_1,Group_2 Item_14 0.046 0.012 0.108 5.682 2 0.058
#> 15 Group_1,Group_2 Item_15 0.045 0.013 0.103 6.042 2 0.049
#> 16 Group_1,Group_2 Item_16 0.030 0.008 0.100 2.552 2 0.279
#> 17 Group_1,Group_2 Item_17 0.019 0.006 0.087 0.993 2 0.609
#> 18 Group_1,Group_2 Item_18 0.013 0.005 0.081 0.397 2 0.82
#> 19 Group_1,Group_2 Item_19 0.094 0.046 0.145 24.267 2 0
#> 20 Group_1,Group_2 Item_20 0.010 0.004 0.051 0.567 2 0.753
#> 21 Group_1,Group_2 Item_21 0.070 0.016 0.132 10.313 2 0.006
#> 22 Group_1,Group_2 Item_22 0.020 0.007 0.087 1.063 2 0.588
#> 23 Group_1,Group_2 Item_23 0.064 0.022 0.119 8.042 2 0.018
#> 24 Group_1,Group_2 Item_24 0.040 0.011 0.100 2.796 2 0.247
#> 25 Group_1,Group_2 Item_25 0.018 0.009 0.094 0.869 2 0.648
#> 26 Group_1,Group_2 Item_26 0.047 0.012 0.098 6.435 2 0.04
#> 27 Group_1,Group_2 Item_27 0.049 0.010 0.111 5.453 2 0.065
#> 28 Group_1,Group_2 Item_28 0.029 0.008 0.098 1.636 2 0.441
#> 29 Group_1,Group_2 Item_29 0.025 0.008 0.086 1.641 2 0.44
#> 30 Group_1,Group_2 Item_30 0.031 0.010 0.094 3.233 2 0.199
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.018 0.008 0.098
#> 7 Group_1,Group_2 Item_7 0.028 0.009 0.101
#> 8 Group_1,Group_2 Item_8 0.008 0.006 0.084
#> 9 Group_1,Group_2 Item_9 0.028 0.011 0.102
#> 10 Group_1,Group_2 Item_10 0.044 0.010 0.127
#> 11 Group_1,Group_2 Item_11 0.065 0.015 0.123
#> 12 Group_1,Group_2 Item_12 0.017 0.007 0.091
#> 13 Group_1,Group_2 Item_13 0.025 0.009 0.094
#> 14 Group_1,Group_2 Item_14 0.054 0.014 0.124
#> 15 Group_1,Group_2 Item_15 0.047 0.015 0.112
#> 16 Group_1,Group_2 Item_16 0.032 0.009 0.109
#> 17 Group_1,Group_2 Item_17 0.023 0.007 0.101
#> 18 Group_1,Group_2 Item_18 0.014 0.006 0.091
#> 19 Group_1,Group_2 Item_19 0.117 0.058 0.179
#> 20 Group_1,Group_2 Item_20 0.010 0.005 0.079
#> 21 Group_1,Group_2 Item_21 0.073 0.017 0.140
#> 22 Group_1,Group_2 Item_22 0.024 0.008 0.097
#> 23 Group_1,Group_2 Item_23 0.078 0.025 0.140
#> 24 Group_1,Group_2 Item_24 0.042 0.012 0.108
#> 25 Group_1,Group_2 Item_25 0.021 0.010 0.102
#> 26 Group_1,Group_2 Item_26 0.065 0.015 0.130
#> 27 Group_1,Group_2 Item_27 0.052 0.012 0.122
#> 28 Group_1,Group_2 Item_28 0.031 0.010 0.106
#> 29 Group_1,Group_2 Item_29 0.028 0.009 0.096
#> 30 Group_1,Group_2 Item_30 0.033 0.011 0.100
#>
DRF(mod, focal_items = 6:10, param_set=param_set) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 5 -0.069 -0.242 0.119 0.569 1 0.451
#> uDRF Group_1,Group_2 5 0.071 0.018 0.249 2.054 2 0.358
#> dDRF Group_1,Group_2 5 0.084 0.023 0.285
DRF(mod, param_set=param_set) #DTF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -1.036 0.404 0.876 1 0.349
#> uDRF Group_1,Group_2 30 0.326 0.099 1.047 2.483 2 0.289
#> dDRF Group_1,Group_2 30 0.328 0.127 1.130
DRF(mod, focal_items = 6:10, draws=500) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 5 -0.069 -0.239 0.094 0.658 1 0.417
#> uDRF Group_1,Group_2 5 0.071 0.020 0.254 2.171 2 0.338
#> dDRF Group_1,Group_2 5 0.084 0.023 0.295
DRF(mod, focal_items = 10:15, draws=500) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 6 -0.175 -0.382 0.024 2.99 1 0.084
#> uDRF Group_1,Group_2 6 0.175 0.047 0.392 7.227 2 0.027
#> dDRF Group_1,Group_2 6 0.185 0.054 0.415
DIFs <- DRF(mod, draws = 500, DIF=TRUE)
print(DIFs)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 -0.058 0.062 0 1 0.998
#> 7 Group_1,Group_2 Item_7 -0.026 -0.087 0.035 0.717 1 0.397
#> 8 Group_1,Group_2 Item_8 -0.008 -0.075 0.053 0.058 1 0.809
#> 9 Group_1,Group_2 Item_9 -0.026 -0.084 0.044 0.718 1 0.397
#> 10 Group_1,Group_2 Item_10 -0.010 -0.063 0.041 0.12 1 0.729
#> 11 Group_1,Group_2 Item_11 -0.056 -0.118 0.003 3.206 1 0.073
#> 12 Group_1,Group_2 Item_12 -0.016 -0.078 0.041 0.288 1 0.591
#> 13 Group_1,Group_2 Item_13 -0.015 -0.073 0.042 0.261 1 0.609
#> 14 Group_1,Group_2 Item_14 -0.033 -0.097 0.036 1.077 1 0.299
#> 15 Group_1,Group_2 Item_15 -0.045 -0.101 0.013 2.453 1 0.117
#> 16 Group_1,Group_2 Item_16 -0.030 -0.096 0.033 0.87 1 0.351
#> 17 Group_1,Group_2 Item_17 0.018 -0.041 0.076 0.317 1 0.573
#> 18 Group_1,Group_2 Item_18 0.011 -0.051 0.068 0.131 1 0.718
#> 19 Group_1,Group_2 Item_19 -0.045 -0.105 0.012 2.273 1 0.132
#> 20 Group_1,Group_2 Item_20 -0.008 -0.044 0.039 0.149 1 0.699
#> 21 Group_1,Group_2 Item_21 -0.070 -0.128 -0.007 5.598 1 0.018
#> 22 Group_1,Group_2 Item_22 0.017 -0.044 0.084 0.294 1 0.588
#> 23 Group_1,Group_2 Item_23 0.036 -0.027 0.100 1.299 1 0.254
#> 24 Group_1,Group_2 Item_24 0.040 -0.026 0.112 1.451 1 0.228
#> 25 Group_1,Group_2 Item_25 0.002 -0.064 0.061 0.004 1 0.948
#> 26 Group_1,Group_2 Item_26 -0.019 -0.069 0.032 0.458 1 0.499
#> 27 Group_1,Group_2 Item_27 -0.049 -0.108 0.016 2.686 1 0.101
#> 28 Group_1,Group_2 Item_28 0.027 -0.028 0.087 0.835 1 0.361
#> 29 Group_1,Group_2 Item_29 0.007 -0.058 0.072 0.053 1 0.819
#> 30 Group_1,Group_2 Item_30 -0.029 -0.088 0.029 0.947 1 0.331
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.016 0.005 0.083 0.763 2 0.683
#> 7 Group_1,Group_2 Item_7 0.026 0.007 0.087 2.145 2 0.342
#> 8 Group_1,Group_2 Item_8 0.008 0.007 0.083 0.189 2 0.91
#> 9 Group_1,Group_2 Item_9 0.026 0.009 0.090 2.362 2 0.307
#> 10 Group_1,Group_2 Item_10 0.036 0.008 0.094 3.757 2 0.153
#> 11 Group_1,Group_2 Item_11 0.059 0.018 0.119 9.246 2 0.01
#> 12 Group_1,Group_2 Item_12 0.016 0.008 0.081 0.892 2 0.64
#> 13 Group_1,Group_2 Item_13 0.022 0.007 0.079 1.963 2 0.375
#> 14 Group_1,Group_2 Item_14 0.046 0.011 0.109 5.685 2 0.058
#> 15 Group_1,Group_2 Item_15 0.045 0.012 0.101 5.995 2 0.05
#> 16 Group_1,Group_2 Item_16 0.030 0.008 0.096 2.457 2 0.293
#> 17 Group_1,Group_2 Item_17 0.019 0.007 0.084 1.06 2 0.589
#> 18 Group_1,Group_2 Item_18 0.013 0.007 0.078 0.44 2 0.803
#> 19 Group_1,Group_2 Item_19 0.094 0.047 0.148 22.435 2 0
#> 20 Group_1,Group_2 Item_20 0.010 0.004 0.053 0.533 2 0.766
#> 21 Group_1,Group_2 Item_21 0.070 0.022 0.129 12.43 2 0.002
#> 22 Group_1,Group_2 Item_22 0.020 0.006 0.089 1.016 2 0.602
#> 23 Group_1,Group_2 Item_23 0.064 0.018 0.121 7.163 2 0.028
#> 24 Group_1,Group_2 Item_24 0.040 0.008 0.112 2.247 2 0.325
#> 25 Group_1,Group_2 Item_25 0.018 0.006 0.086 0.919 2 0.632
#> 26 Group_1,Group_2 Item_26 0.047 0.013 0.096 6.626 2 0.036
#> 27 Group_1,Group_2 Item_27 0.049 0.013 0.108 6.465 2 0.039
#> 28 Group_1,Group_2 Item_28 0.029 0.010 0.088 1.806 2 0.405
#> 29 Group_1,Group_2 Item_29 0.025 0.009 0.085 1.805 2 0.406
#> 30 Group_1,Group_2 Item_30 0.031 0.008 0.093 3.105 2 0.212
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.018 0.006 0.092
#> 7 Group_1,Group_2 Item_7 0.028 0.008 0.095
#> 8 Group_1,Group_2 Item_8 0.008 0.007 0.094
#> 9 Group_1,Group_2 Item_9 0.028 0.011 0.097
#> 10 Group_1,Group_2 Item_10 0.044 0.010 0.114
#> 11 Group_1,Group_2 Item_11 0.065 0.020 0.131
#> 12 Group_1,Group_2 Item_12 0.017 0.009 0.088
#> 13 Group_1,Group_2 Item_13 0.025 0.008 0.088
#> 14 Group_1,Group_2 Item_14 0.054 0.013 0.126
#> 15 Group_1,Group_2 Item_15 0.047 0.014 0.111
#> 16 Group_1,Group_2 Item_16 0.032 0.009 0.103
#> 17 Group_1,Group_2 Item_17 0.023 0.008 0.096
#> 18 Group_1,Group_2 Item_18 0.014 0.008 0.091
#> 19 Group_1,Group_2 Item_19 0.117 0.056 0.183
#> 20 Group_1,Group_2 Item_20 0.010 0.006 0.079
#> 21 Group_1,Group_2 Item_21 0.073 0.025 0.138
#> 22 Group_1,Group_2 Item_22 0.024 0.007 0.099
#> 23 Group_1,Group_2 Item_23 0.078 0.019 0.144
#> 24 Group_1,Group_2 Item_24 0.042 0.009 0.118
#> 25 Group_1,Group_2 Item_25 0.021 0.007 0.104
#> 26 Group_1,Group_2 Item_26 0.065 0.017 0.135
#> 27 Group_1,Group_2 Item_27 0.052 0.014 0.118
#> 28 Group_1,Group_2 Item_28 0.031 0.011 0.099
#> 29 Group_1,Group_2 Item_29 0.028 0.010 0.095
#> 30 Group_1,Group_2 Item_30 0.033 0.009 0.101
#>
DRF(mod, draws = 500, DIF=TRUE, plot=TRUE)
# pre-draw parameter set to save computations
# (more useful when using non-parametric bootstrap)
param_set <- draw_parameters(mod, draws = 500)
DRF(mod, focal_items = 6, param_set=param_set) #DIF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 1 0.000 -0.058 0.066 0 1 0.999
#> uDRF Group_1,Group_2 1 0.016 0.007 0.085 0.768 2 0.681
#> dDRF Group_1,Group_2 1 0.018 0.008 0.098
DRF(mod, DIF=TRUE, param_set=param_set) #DIF test
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 -0.058 0.066 0 1 0.999
#> 7 Group_1,Group_2 Item_7 -0.026 -0.087 0.040 0.653 1 0.419
#> 8 Group_1,Group_2 Item_8 -0.008 -0.060 0.058 0.066 1 0.798
#> 9 Group_1,Group_2 Item_9 -0.026 -0.091 0.031 0.649 1 0.421
#> 10 Group_1,Group_2 Item_10 -0.010 -0.072 0.048 0.101 1 0.751
#> 11 Group_1,Group_2 Item_11 -0.056 -0.116 0.003 3.557 1 0.059
#> 12 Group_1,Group_2 Item_12 -0.016 -0.074 0.038 0.305 1 0.581
#> 13 Group_1,Group_2 Item_13 -0.015 -0.075 0.041 0.234 1 0.629
#> 14 Group_1,Group_2 Item_14 -0.033 -0.096 0.027 1.029 1 0.31
#> 15 Group_1,Group_2 Item_15 -0.045 -0.103 0.012 2.479 1 0.115
#> 16 Group_1,Group_2 Item_16 -0.030 -0.098 0.036 0.883 1 0.348
#> 17 Group_1,Group_2 Item_17 0.018 -0.042 0.079 0.31 1 0.578
#> 18 Group_1,Group_2 Item_18 0.011 -0.051 0.072 0.125 1 0.723
#> 19 Group_1,Group_2 Item_19 -0.045 -0.103 0.011 2.293 1 0.13
#> 20 Group_1,Group_2 Item_20 -0.008 -0.045 0.034 0.159 1 0.69
#> 21 Group_1,Group_2 Item_21 -0.070 -0.133 -0.006 4.678 1 0.031
#> 22 Group_1,Group_2 Item_22 0.017 -0.048 0.071 0.312 1 0.576
#> 23 Group_1,Group_2 Item_23 0.036 -0.031 0.098 1.291 1 0.256
#> 24 Group_1,Group_2 Item_24 0.040 -0.021 0.097 1.787 1 0.181
#> 25 Group_1,Group_2 Item_25 0.002 -0.062 0.061 0.004 1 0.949
#> 26 Group_1,Group_2 Item_26 -0.019 -0.075 0.037 0.471 1 0.493
#> 27 Group_1,Group_2 Item_27 -0.049 -0.111 0.014 2.298 1 0.13
#> 28 Group_1,Group_2 Item_28 0.027 -0.036 0.090 0.681 1 0.409
#> 29 Group_1,Group_2 Item_29 0.007 -0.057 0.073 0.05 1 0.824
#> 30 Group_1,Group_2 Item_30 -0.029 -0.092 0.022 1.002 1 0.317
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.016 0.007 0.085 0.768 2 0.681
#> 7 Group_1,Group_2 Item_7 0.026 0.008 0.090 1.944 2 0.378
#> 8 Group_1,Group_2 Item_8 0.008 0.005 0.073 0.225 2 0.893
#> 9 Group_1,Group_2 Item_9 0.026 0.008 0.093 2.093 2 0.351
#> 10 Group_1,Group_2 Item_10 0.036 0.008 0.107 3.281 2 0.194
#> 11 Group_1,Group_2 Item_11 0.059 0.015 0.113 10.147 2 0.006
#> 12 Group_1,Group_2 Item_12 0.016 0.005 0.074 0.849 2 0.654
#> 13 Group_1,Group_2 Item_13 0.022 0.007 0.084 1.69 2 0.43
#> 14 Group_1,Group_2 Item_14 0.046 0.012 0.108 5.682 2 0.058
#> 15 Group_1,Group_2 Item_15 0.045 0.013 0.103 6.042 2 0.049
#> 16 Group_1,Group_2 Item_16 0.030 0.008 0.100 2.552 2 0.279
#> 17 Group_1,Group_2 Item_17 0.019 0.006 0.087 0.993 2 0.609
#> 18 Group_1,Group_2 Item_18 0.013 0.005 0.081 0.397 2 0.82
#> 19 Group_1,Group_2 Item_19 0.094 0.046 0.145 24.267 2 0
#> 20 Group_1,Group_2 Item_20 0.010 0.004 0.051 0.567 2 0.753
#> 21 Group_1,Group_2 Item_21 0.070 0.016 0.132 10.313 2 0.006
#> 22 Group_1,Group_2 Item_22 0.020 0.007 0.087 1.063 2 0.588
#> 23 Group_1,Group_2 Item_23 0.064 0.022 0.119 8.042 2 0.018
#> 24 Group_1,Group_2 Item_24 0.040 0.011 0.100 2.796 2 0.247
#> 25 Group_1,Group_2 Item_25 0.018 0.009 0.094 0.869 2 0.648
#> 26 Group_1,Group_2 Item_26 0.047 0.012 0.098 6.435 2 0.04
#> 27 Group_1,Group_2 Item_27 0.049 0.010 0.111 5.453 2 0.065
#> 28 Group_1,Group_2 Item_28 0.029 0.008 0.098 1.636 2 0.441
#> 29 Group_1,Group_2 Item_29 0.025 0.008 0.086 1.641 2 0.44
#> 30 Group_1,Group_2 Item_30 0.031 0.010 0.094 3.233 2 0.199
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.018 0.008 0.098
#> 7 Group_1,Group_2 Item_7 0.028 0.009 0.101
#> 8 Group_1,Group_2 Item_8 0.008 0.006 0.084
#> 9 Group_1,Group_2 Item_9 0.028 0.011 0.102
#> 10 Group_1,Group_2 Item_10 0.044 0.010 0.127
#> 11 Group_1,Group_2 Item_11 0.065 0.015 0.123
#> 12 Group_1,Group_2 Item_12 0.017 0.007 0.091
#> 13 Group_1,Group_2 Item_13 0.025 0.009 0.094
#> 14 Group_1,Group_2 Item_14 0.054 0.014 0.124
#> 15 Group_1,Group_2 Item_15 0.047 0.015 0.112
#> 16 Group_1,Group_2 Item_16 0.032 0.009 0.109
#> 17 Group_1,Group_2 Item_17 0.023 0.007 0.101
#> 18 Group_1,Group_2 Item_18 0.014 0.006 0.091
#> 19 Group_1,Group_2 Item_19 0.117 0.058 0.179
#> 20 Group_1,Group_2 Item_20 0.010 0.005 0.079
#> 21 Group_1,Group_2 Item_21 0.073 0.017 0.140
#> 22 Group_1,Group_2 Item_22 0.024 0.008 0.097
#> 23 Group_1,Group_2 Item_23 0.078 0.025 0.140
#> 24 Group_1,Group_2 Item_24 0.042 0.012 0.108
#> 25 Group_1,Group_2 Item_25 0.021 0.010 0.102
#> 26 Group_1,Group_2 Item_26 0.065 0.015 0.130
#> 27 Group_1,Group_2 Item_27 0.052 0.012 0.122
#> 28 Group_1,Group_2 Item_28 0.031 0.010 0.106
#> 29 Group_1,Group_2 Item_29 0.028 0.009 0.096
#> 30 Group_1,Group_2 Item_30 0.033 0.011 0.100
#>
DRF(mod, focal_items = 6:10, param_set=param_set) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 5 -0.069 -0.242 0.119 0.569 1 0.451
#> uDRF Group_1,Group_2 5 0.071 0.018 0.249 2.054 2 0.358
#> dDRF Group_1,Group_2 5 0.084 0.023 0.285
DRF(mod, param_set=param_set) #DTF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.326 -1.036 0.404 0.876 1 0.349
#> uDRF Group_1,Group_2 30 0.326 0.099 1.047 2.483 2 0.289
#> dDRF Group_1,Group_2 30 0.328 0.127 1.130
DRF(mod, focal_items = 6:10, draws=500) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 5 -0.069 -0.239 0.094 0.658 1 0.417
#> uDRF Group_1,Group_2 5 0.071 0.020 0.254 2.171 2 0.338
#> dDRF Group_1,Group_2 5 0.084 0.023 0.295
DRF(mod, focal_items = 10:15, draws=500) #DBF test
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 6 -0.175 -0.382 0.024 2.99 1 0.084
#> uDRF Group_1,Group_2 6 0.175 0.047 0.392 7.227 2 0.027
#> dDRF Group_1,Group_2 6 0.185 0.054 0.415
DIFs <- DRF(mod, draws = 500, DIF=TRUE)
print(DIFs)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.000 -0.058 0.062 0 1 0.998
#> 7 Group_1,Group_2 Item_7 -0.026 -0.087 0.035 0.717 1 0.397
#> 8 Group_1,Group_2 Item_8 -0.008 -0.075 0.053 0.058 1 0.809
#> 9 Group_1,Group_2 Item_9 -0.026 -0.084 0.044 0.718 1 0.397
#> 10 Group_1,Group_2 Item_10 -0.010 -0.063 0.041 0.12 1 0.729
#> 11 Group_1,Group_2 Item_11 -0.056 -0.118 0.003 3.206 1 0.073
#> 12 Group_1,Group_2 Item_12 -0.016 -0.078 0.041 0.288 1 0.591
#> 13 Group_1,Group_2 Item_13 -0.015 -0.073 0.042 0.261 1 0.609
#> 14 Group_1,Group_2 Item_14 -0.033 -0.097 0.036 1.077 1 0.299
#> 15 Group_1,Group_2 Item_15 -0.045 -0.101 0.013 2.453 1 0.117
#> 16 Group_1,Group_2 Item_16 -0.030 -0.096 0.033 0.87 1 0.351
#> 17 Group_1,Group_2 Item_17 0.018 -0.041 0.076 0.317 1 0.573
#> 18 Group_1,Group_2 Item_18 0.011 -0.051 0.068 0.131 1 0.718
#> 19 Group_1,Group_2 Item_19 -0.045 -0.105 0.012 2.273 1 0.132
#> 20 Group_1,Group_2 Item_20 -0.008 -0.044 0.039 0.149 1 0.699
#> 21 Group_1,Group_2 Item_21 -0.070 -0.128 -0.007 5.598 1 0.018
#> 22 Group_1,Group_2 Item_22 0.017 -0.044 0.084 0.294 1 0.588
#> 23 Group_1,Group_2 Item_23 0.036 -0.027 0.100 1.299 1 0.254
#> 24 Group_1,Group_2 Item_24 0.040 -0.026 0.112 1.451 1 0.228
#> 25 Group_1,Group_2 Item_25 0.002 -0.064 0.061 0.004 1 0.948
#> 26 Group_1,Group_2 Item_26 -0.019 -0.069 0.032 0.458 1 0.499
#> 27 Group_1,Group_2 Item_27 -0.049 -0.108 0.016 2.686 1 0.101
#> 28 Group_1,Group_2 Item_28 0.027 -0.028 0.087 0.835 1 0.361
#> 29 Group_1,Group_2 Item_29 0.007 -0.058 0.072 0.053 1 0.819
#> 30 Group_1,Group_2 Item_30 -0.029 -0.088 0.029 0.947 1 0.331
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.016 0.005 0.083 0.763 2 0.683
#> 7 Group_1,Group_2 Item_7 0.026 0.007 0.087 2.145 2 0.342
#> 8 Group_1,Group_2 Item_8 0.008 0.007 0.083 0.189 2 0.91
#> 9 Group_1,Group_2 Item_9 0.026 0.009 0.090 2.362 2 0.307
#> 10 Group_1,Group_2 Item_10 0.036 0.008 0.094 3.757 2 0.153
#> 11 Group_1,Group_2 Item_11 0.059 0.018 0.119 9.246 2 0.01
#> 12 Group_1,Group_2 Item_12 0.016 0.008 0.081 0.892 2 0.64
#> 13 Group_1,Group_2 Item_13 0.022 0.007 0.079 1.963 2 0.375
#> 14 Group_1,Group_2 Item_14 0.046 0.011 0.109 5.685 2 0.058
#> 15 Group_1,Group_2 Item_15 0.045 0.012 0.101 5.995 2 0.05
#> 16 Group_1,Group_2 Item_16 0.030 0.008 0.096 2.457 2 0.293
#> 17 Group_1,Group_2 Item_17 0.019 0.007 0.084 1.06 2 0.589
#> 18 Group_1,Group_2 Item_18 0.013 0.007 0.078 0.44 2 0.803
#> 19 Group_1,Group_2 Item_19 0.094 0.047 0.148 22.435 2 0
#> 20 Group_1,Group_2 Item_20 0.010 0.004 0.053 0.533 2 0.766
#> 21 Group_1,Group_2 Item_21 0.070 0.022 0.129 12.43 2 0.002
#> 22 Group_1,Group_2 Item_22 0.020 0.006 0.089 1.016 2 0.602
#> 23 Group_1,Group_2 Item_23 0.064 0.018 0.121 7.163 2 0.028
#> 24 Group_1,Group_2 Item_24 0.040 0.008 0.112 2.247 2 0.325
#> 25 Group_1,Group_2 Item_25 0.018 0.006 0.086 0.919 2 0.632
#> 26 Group_1,Group_2 Item_26 0.047 0.013 0.096 6.626 2 0.036
#> 27 Group_1,Group_2 Item_27 0.049 0.013 0.108 6.465 2 0.039
#> 28 Group_1,Group_2 Item_28 0.029 0.010 0.088 1.806 2 0.405
#> 29 Group_1,Group_2 Item_29 0.025 0.009 0.085 1.805 2 0.406
#> 30 Group_1,Group_2 Item_30 0.031 0.008 0.093 3.105 2 0.212
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_1 0.000 0.000 0.000
#> 2 Group_1,Group_2 Item_2 0.000 0.000 0.000
#> 3 Group_1,Group_2 Item_3 0.000 0.000 0.000
#> 4 Group_1,Group_2 Item_4 0.000 0.000 0.000
#> 5 Group_1,Group_2 Item_5 0.000 0.000 0.000
#> 6 Group_1,Group_2 Item_6 0.018 0.006 0.092
#> 7 Group_1,Group_2 Item_7 0.028 0.008 0.095
#> 8 Group_1,Group_2 Item_8 0.008 0.007 0.094
#> 9 Group_1,Group_2 Item_9 0.028 0.011 0.097
#> 10 Group_1,Group_2 Item_10 0.044 0.010 0.114
#> 11 Group_1,Group_2 Item_11 0.065 0.020 0.131
#> 12 Group_1,Group_2 Item_12 0.017 0.009 0.088
#> 13 Group_1,Group_2 Item_13 0.025 0.008 0.088
#> 14 Group_1,Group_2 Item_14 0.054 0.013 0.126
#> 15 Group_1,Group_2 Item_15 0.047 0.014 0.111
#> 16 Group_1,Group_2 Item_16 0.032 0.009 0.103
#> 17 Group_1,Group_2 Item_17 0.023 0.008 0.096
#> 18 Group_1,Group_2 Item_18 0.014 0.008 0.091
#> 19 Group_1,Group_2 Item_19 0.117 0.056 0.183
#> 20 Group_1,Group_2 Item_20 0.010 0.006 0.079
#> 21 Group_1,Group_2 Item_21 0.073 0.025 0.138
#> 22 Group_1,Group_2 Item_22 0.024 0.007 0.099
#> 23 Group_1,Group_2 Item_23 0.078 0.019 0.144
#> 24 Group_1,Group_2 Item_24 0.042 0.009 0.118
#> 25 Group_1,Group_2 Item_25 0.021 0.007 0.104
#> 26 Group_1,Group_2 Item_26 0.065 0.017 0.135
#> 27 Group_1,Group_2 Item_27 0.052 0.014 0.118
#> 28 Group_1,Group_2 Item_28 0.031 0.011 0.099
#> 29 Group_1,Group_2 Item_29 0.028 0.010 0.095
#> 30 Group_1,Group_2 Item_30 0.033 0.009 0.101
#>
DRF(mod, draws = 500, DIF=TRUE, plot=TRUE)
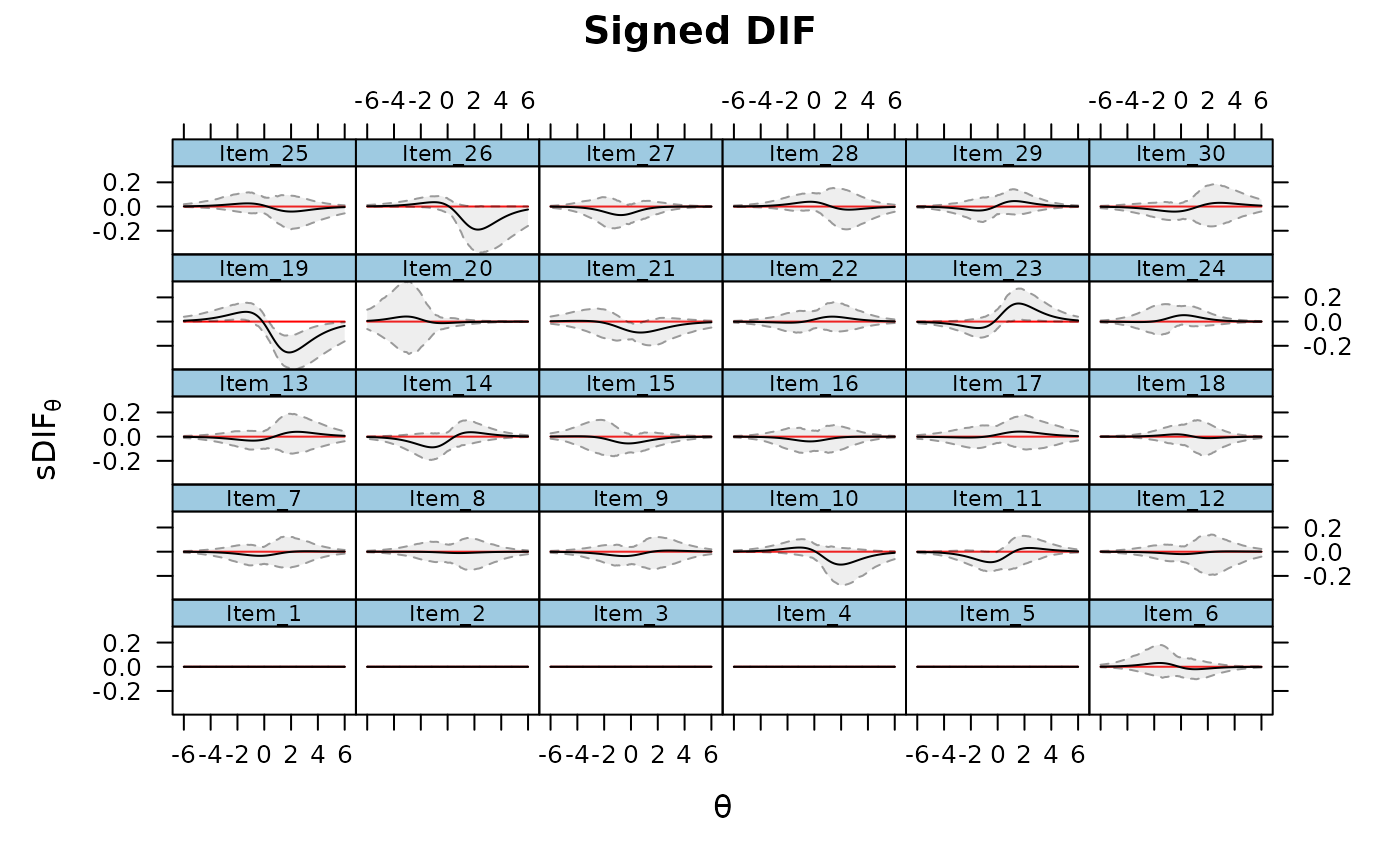 DIFs <- DRF(mod, draws = 500, DIF=TRUE, focal_items = 6:10)
print(DIFs)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.000 -0.066 0.064 0 1 0.998
#> 2 Group_1,Group_2 Item_7 -0.026 -0.083 0.040 0.697 1 0.404
#> 3 Group_1,Group_2 Item_8 -0.008 -0.074 0.045 0.062 1 0.803
#> 4 Group_1,Group_2 Item_9 -0.026 -0.089 0.037 0.739 1 0.39
#> 5 Group_1,Group_2 Item_10 -0.010 -0.070 0.045 0.113 1 0.737
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.016 0.006 0.081 0.788 2 0.674
#> 2 Group_1,Group_2 Item_7 0.026 0.007 0.090 2.051 2 0.359
#> 3 Group_1,Group_2 Item_8 0.008 0.007 0.080 0.216 2 0.898
#> 4 Group_1,Group_2 Item_9 0.026 0.007 0.089 2.358 2 0.308
#> 5 Group_1,Group_2 Item_10 0.036 0.008 0.093 3.284 2 0.194
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_6 0.018 0.007 0.092
#> 2 Group_1,Group_2 Item_7 0.028 0.008 0.100
#> 3 Group_1,Group_2 Item_8 0.008 0.008 0.090
#> 4 Group_1,Group_2 Item_9 0.028 0.008 0.096
#> 5 Group_1,Group_2 Item_10 0.044 0.009 0.121
#>
DRF(mod, draws = 500, DIF=TRUE, focal_items = 6:10, plot = TRUE)
DIFs <- DRF(mod, draws = 500, DIF=TRUE, focal_items = 6:10)
print(DIFs)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.000 -0.066 0.064 0 1 0.998
#> 2 Group_1,Group_2 Item_7 -0.026 -0.083 0.040 0.697 1 0.404
#> 3 Group_1,Group_2 Item_8 -0.008 -0.074 0.045 0.062 1 0.803
#> 4 Group_1,Group_2 Item_9 -0.026 -0.089 0.037 0.739 1 0.39
#> 5 Group_1,Group_2 Item_10 -0.010 -0.070 0.045 0.113 1 0.737
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.016 0.006 0.081 0.788 2 0.674
#> 2 Group_1,Group_2 Item_7 0.026 0.007 0.090 2.051 2 0.359
#> 3 Group_1,Group_2 Item_8 0.008 0.007 0.080 0.216 2 0.898
#> 4 Group_1,Group_2 Item_9 0.026 0.007 0.089 2.358 2 0.308
#> 5 Group_1,Group_2 Item_10 0.036 0.008 0.093 3.284 2 0.194
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_6 0.018 0.007 0.092
#> 2 Group_1,Group_2 Item_7 0.028 0.008 0.100
#> 3 Group_1,Group_2 Item_8 0.008 0.008 0.090
#> 4 Group_1,Group_2 Item_9 0.028 0.008 0.096
#> 5 Group_1,Group_2 Item_10 0.044 0.009 0.121
#>
DRF(mod, draws = 500, DIF=TRUE, focal_items = 6:10, plot = TRUE)
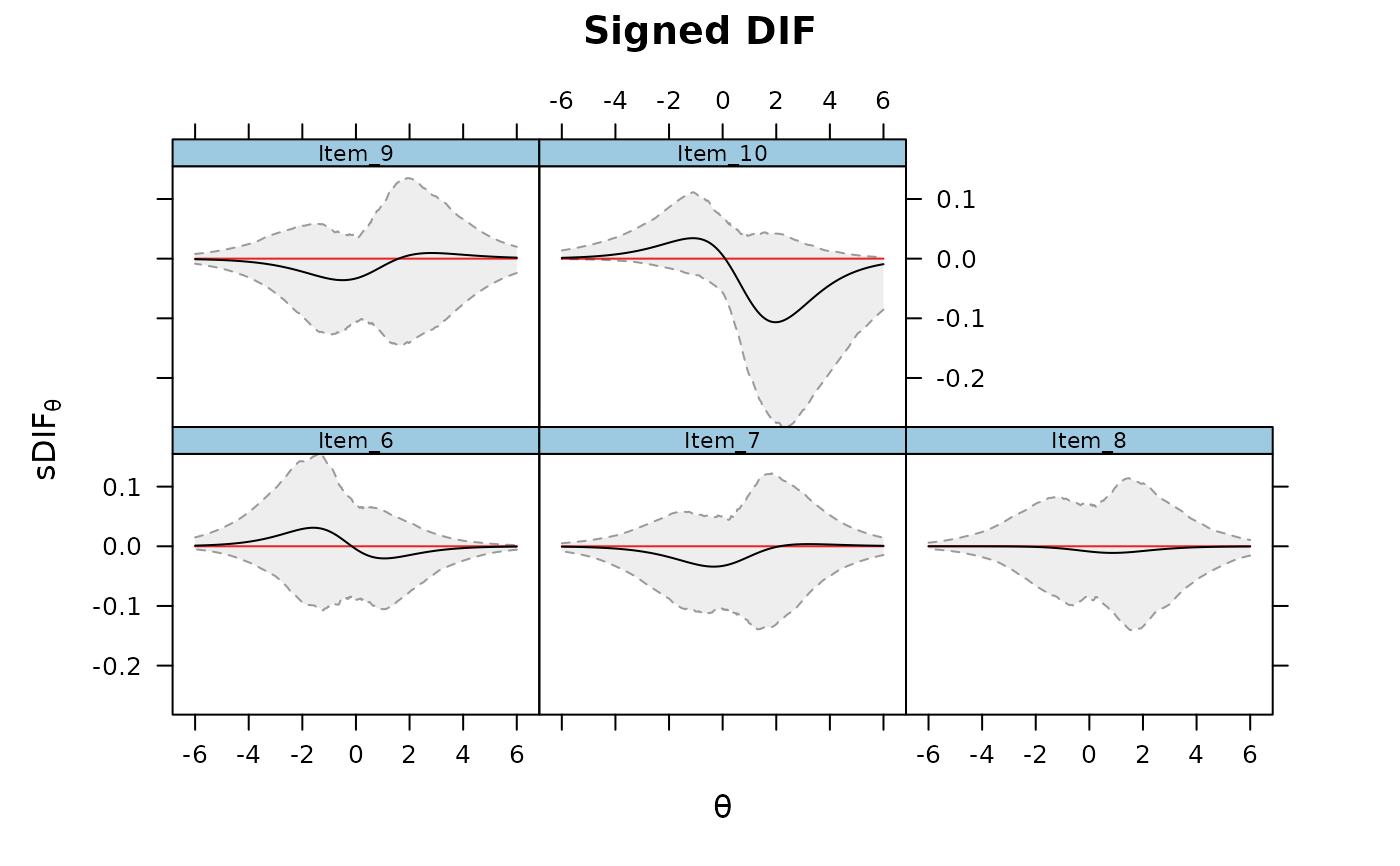 DRF(mod, DIF=TRUE, focal_items = 6)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_6 0 0.016 0.018
DRF(mod, draws=500, DIF=TRUE, focal_items = 6)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0 -0.059 0.058 0 1 0.998
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.016 0.006 0.076 0.825 2 0.662
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_6 0.018 0.006 0.088
#>
# evaluate specific values for sDRF
Theta_nodes <- matrix(seq(-6,6,length.out = 100))
sDTF <- DRF(mod, Theta_nodes=Theta_nodes)
head(sDTF)
#> Theta sDRF
#> sDRF.1 -6.000 0.006
#> sDRF.2 -5.879 0.006
#> sDRF.3 -5.758 0.007
#> sDRF.4 -5.636 0.007
#> sDRF.5 -5.515 0.007
#> sDRF.6 -5.394 0.008
sDTF <- DRF(mod, Theta_nodes=Theta_nodes, draws=200)
head(sDTF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 0.006 -0.076 0.185
#> sDRF.2 -5.879 0.006 -0.083 0.199
#> sDRF.3 -5.758 0.007 -0.090 0.214
#> sDRF.4 -5.636 0.007 -0.098 0.230
#> sDRF.5 -5.515 0.007 -0.107 0.243
#> sDRF.6 -5.394 0.008 -0.117 0.256
# sDIF (isolate single item)
sDIF <- DRF(mod, Theta_nodes=Theta_nodes, focal_items=6)
head(sDIF)
#> Theta sDRF
#> sDRF.1 -6.000 0.001
#> sDRF.2 -5.879 0.001
#> sDRF.3 -5.758 0.001
#> sDRF.4 -5.636 0.002
#> sDRF.5 -5.515 0.002
#> sDRF.6 -5.394 0.002
sDIF <- DRF(mod, Theta_nodes=Theta_nodes, focal_items = 6, draws=200)
head(sDIF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 0.001 -0.005 0.013
#> sDRF.2 -5.879 0.001 -0.005 0.014
#> sDRF.3 -5.758 0.001 -0.006 0.015
#> sDRF.4 -5.636 0.002 -0.006 0.017
#> sDRF.5 -5.515 0.002 -0.007 0.018
#> sDRF.6 -5.394 0.002 -0.008 0.020
## -------------
## random slopes and intercepts for 15 items, and latent mean difference
## (no systematic DTF should exist, but DIF will be present)
set.seed(1234)
dat1 <- simdata(a, d, N, itemtype = 'dich', mu=.50, sigma=matrix(1.5))
dat2 <- simdata(a + c(numeric(15), rnorm(n-15, 0, .25)),
d + c(numeric(15), rnorm(n-15, 0, .5)), N, itemtype = 'dich')
dat <- rbind(dat1, dat2)
mod1 <- multipleGroup(dat, 1, group=group)
plot(mod1)
DRF(mod, DIF=TRUE, focal_items = 6)
#> groups item sDIF uDIF dDIF
#> 1 Group_1,Group_2 Item_6 0 0.016 0.018
DRF(mod, draws=500, DIF=TRUE, focal_items = 6)
#> $sDIF
#> groups item sDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0 -0.059 0.058 0 1 0.998
#>
#> $uDIF
#> groups item uDIF CI_2.5 CI_97.5 X2 df p
#> 1 Group_1,Group_2 Item_6 0.016 0.006 0.076 0.825 2 0.662
#>
#> $dDIF
#> groups item dDIF CI_2.5 CI_97.5
#> 1 Group_1,Group_2 Item_6 0.018 0.006 0.088
#>
# evaluate specific values for sDRF
Theta_nodes <- matrix(seq(-6,6,length.out = 100))
sDTF <- DRF(mod, Theta_nodes=Theta_nodes)
head(sDTF)
#> Theta sDRF
#> sDRF.1 -6.000 0.006
#> sDRF.2 -5.879 0.006
#> sDRF.3 -5.758 0.007
#> sDRF.4 -5.636 0.007
#> sDRF.5 -5.515 0.007
#> sDRF.6 -5.394 0.008
sDTF <- DRF(mod, Theta_nodes=Theta_nodes, draws=200)
head(sDTF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 0.006 -0.076 0.185
#> sDRF.2 -5.879 0.006 -0.083 0.199
#> sDRF.3 -5.758 0.007 -0.090 0.214
#> sDRF.4 -5.636 0.007 -0.098 0.230
#> sDRF.5 -5.515 0.007 -0.107 0.243
#> sDRF.6 -5.394 0.008 -0.117 0.256
# sDIF (isolate single item)
sDIF <- DRF(mod, Theta_nodes=Theta_nodes, focal_items=6)
head(sDIF)
#> Theta sDRF
#> sDRF.1 -6.000 0.001
#> sDRF.2 -5.879 0.001
#> sDRF.3 -5.758 0.001
#> sDRF.4 -5.636 0.002
#> sDRF.5 -5.515 0.002
#> sDRF.6 -5.394 0.002
sDIF <- DRF(mod, Theta_nodes=Theta_nodes, focal_items = 6, draws=200)
head(sDIF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 0.001 -0.005 0.013
#> sDRF.2 -5.879 0.001 -0.005 0.014
#> sDRF.3 -5.758 0.001 -0.006 0.015
#> sDRF.4 -5.636 0.002 -0.006 0.017
#> sDRF.5 -5.515 0.002 -0.007 0.018
#> sDRF.6 -5.394 0.002 -0.008 0.020
## -------------
## random slopes and intercepts for 15 items, and latent mean difference
## (no systematic DTF should exist, but DIF will be present)
set.seed(1234)
dat1 <- simdata(a, d, N, itemtype = 'dich', mu=.50, sigma=matrix(1.5))
dat2 <- simdata(a + c(numeric(15), rnorm(n-15, 0, .25)),
d + c(numeric(15), rnorm(n-15, 0, .5)), N, itemtype = 'dich')
dat <- rbind(dat1, dat2)
mod1 <- multipleGroup(dat, 1, group=group)
plot(mod1)
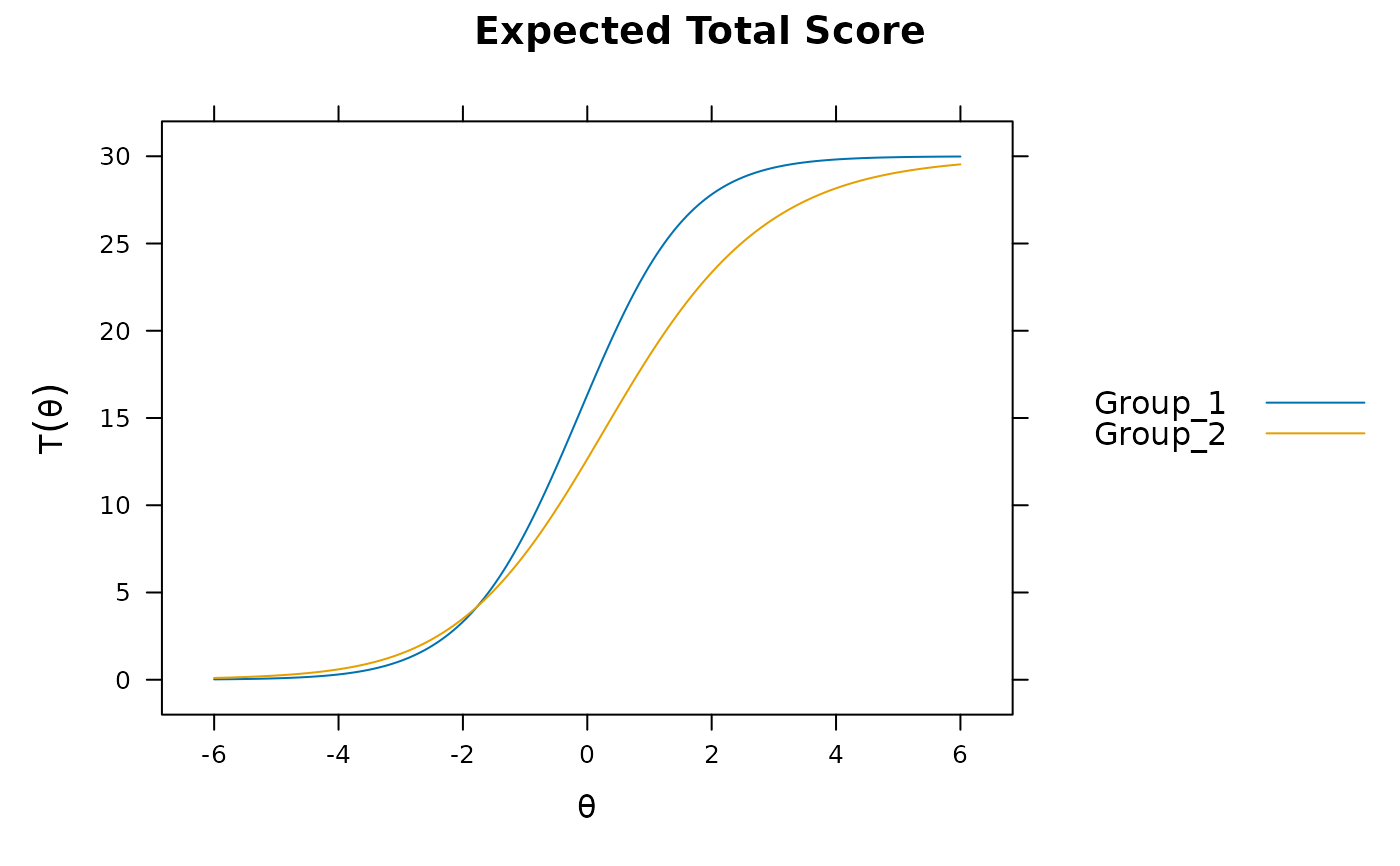 DRF(mod1) #does not account for group differences! Need anchors
#> No hyper-parameters were estimated in the DIF model. For effective
#> DRF testing freeing the focal group hyper-parameters is recommended.
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -3.25 3.268 3.642
mod2 <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
plot(mod2)
DRF(mod1) #does not account for group differences! Need anchors
#> No hyper-parameters were estimated in the DIF model. For effective
#> DRF testing freeing the focal group hyper-parameters is recommended.
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -3.25 3.268 3.642
mod2 <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
plot(mod2)
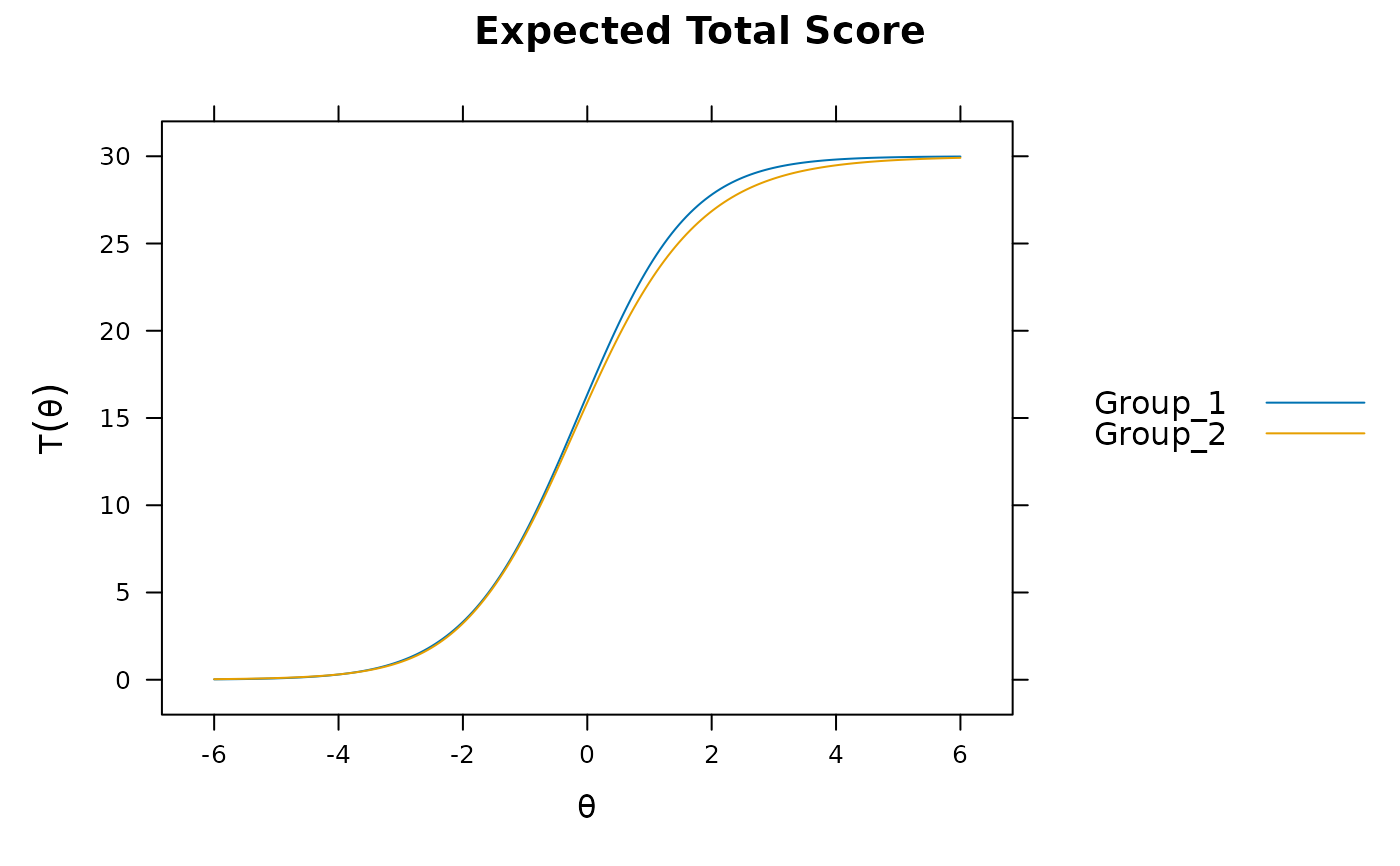 # significant DIF in multiple items....
# DIF(mod2, which.par=c('a1', 'd'), items2test=16:30)
DRF(mod2)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.421 0.421 0.51
DRF(mod2, draws=500) #non-sig DTF due to item cancellation
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.421 -1.085 0.273 1.529 1 0.216
#> uDRF Group_1,Group_2 30 0.421 0.136 1.093 4.807 2 0.09
#> dDRF Group_1,Group_2 30 0.510 0.188 1.245
## -------------
## systematic differing slopes and intercepts (clear DTF)
set.seed(1234)
dat1 <- simdata(a, d, N, itemtype = 'dich', mu=.50, sigma=matrix(1.5))
dat2 <- simdata(a + c(numeric(15), rnorm(n-15, 1, .25)),
d + c(numeric(15), rnorm(n-15, 1, .5)),
N, itemtype = 'dich')
dat <- rbind(dat1, dat2)
mod3 <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
plot(mod3) #visable DTF happening
# significant DIF in multiple items....
# DIF(mod2, which.par=c('a1', 'd'), items2test=16:30)
DRF(mod2)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 -0.421 0.421 0.51
DRF(mod2, draws=500) #non-sig DTF due to item cancellation
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 -0.421 -1.085 0.273 1.529 1 0.216
#> uDRF Group_1,Group_2 30 0.421 0.136 1.093 4.807 2 0.09
#> dDRF Group_1,Group_2 30 0.510 0.188 1.245
## -------------
## systematic differing slopes and intercepts (clear DTF)
set.seed(1234)
dat1 <- simdata(a, d, N, itemtype = 'dich', mu=.50, sigma=matrix(1.5))
dat2 <- simdata(a + c(numeric(15), rnorm(n-15, 1, .25)),
d + c(numeric(15), rnorm(n-15, 1, .5)),
N, itemtype = 'dich')
dat <- rbind(dat1, dat2)
mod3 <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
plot(mod3) #visable DTF happening
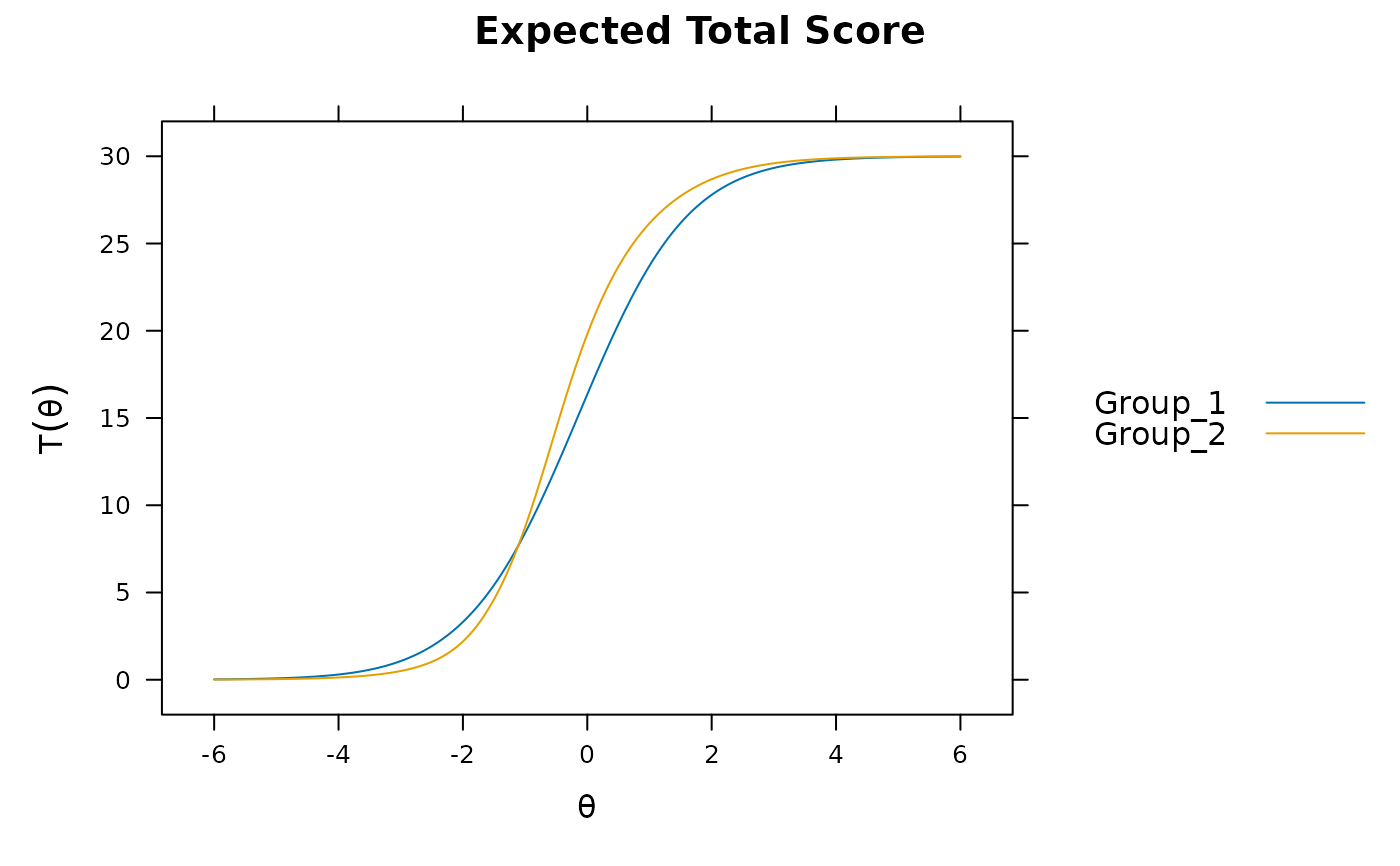 # DIF(mod3, c('a1', 'd'), items2test=16:30)
DRF(mod3) #unsigned bias. Signed bias (group 2 scores higher on average)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 1.983 2.192 2.471
DRF(mod3, draws=500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 1.983 1.275 2.660 29.993 1 0
#> uDRF Group_1,Group_2 30 2.192 1.638 2.836 54.311 2 0
#> dDRF Group_1,Group_2 30 2.471 1.855 3.172
DRF(mod3, draws=500, plot=TRUE) #multiple DRF areas along Theta
# DIF(mod3, c('a1', 'd'), items2test=16:30)
DRF(mod3) #unsigned bias. Signed bias (group 2 scores higher on average)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 30 1.983 2.192 2.471
DRF(mod3, draws=500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 30 1.983 1.275 2.660 29.993 1 0
#> uDRF Group_1,Group_2 30 2.192 1.638 2.836 54.311 2 0
#> dDRF Group_1,Group_2 30 2.471 1.855 3.172
DRF(mod3, draws=500, plot=TRUE) #multiple DRF areas along Theta
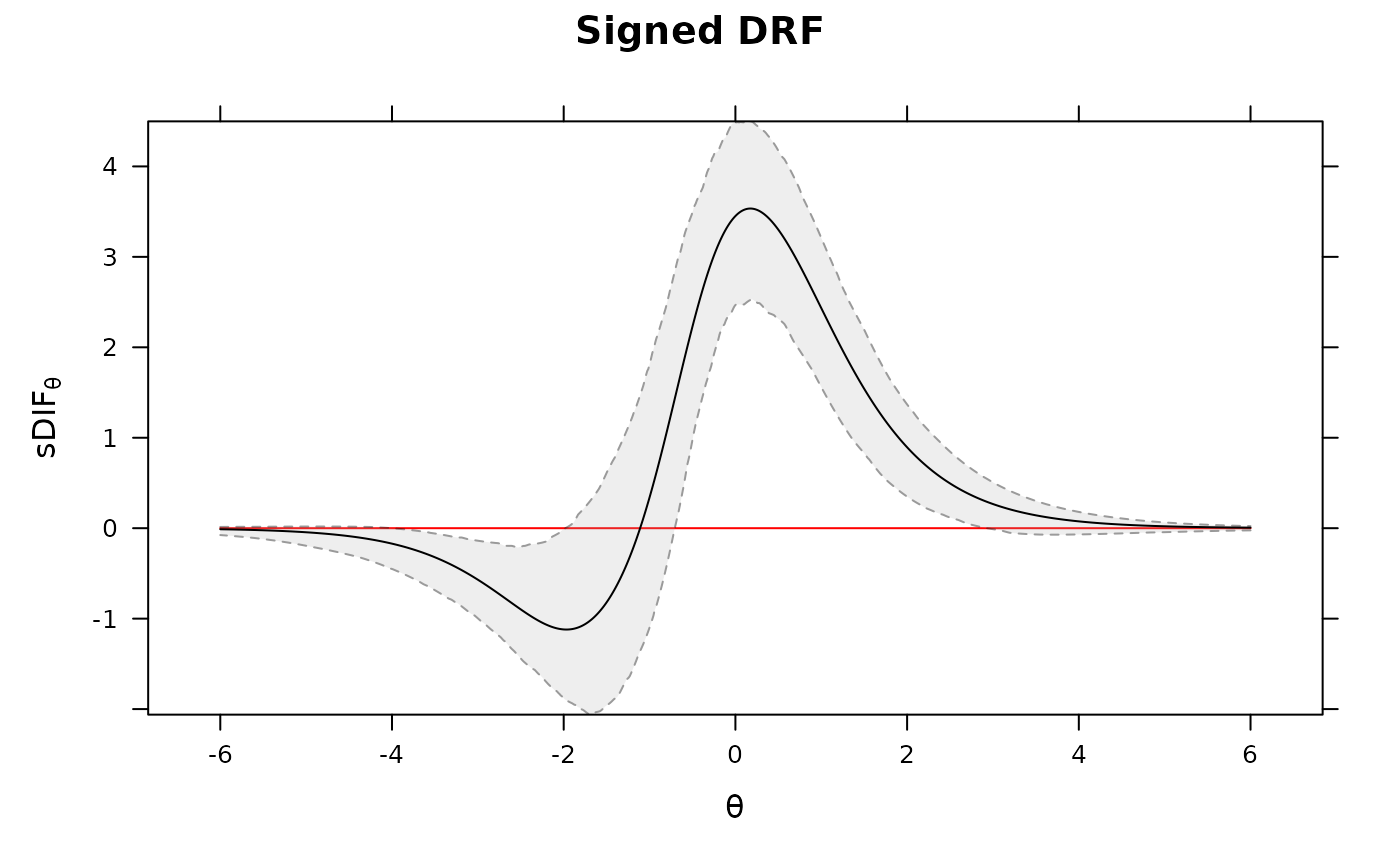 # plot the DIF
DRF(mod3, draws=500, DIF=TRUE, plot=TRUE)
# plot the DIF
DRF(mod3, draws=500, DIF=TRUE, plot=TRUE)
 # evaluate specific values for sDRF
Theta_nodes <- matrix(seq(-6,6,length.out = 100))
sDTF <- DRF(mod3, Theta_nodes=Theta_nodes, draws=200)
head(sDTF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 -0.012 -0.087 0.010
#> sDRF.2 -5.879 -0.014 -0.098 0.010
#> sDRF.3 -5.758 -0.016 -0.109 0.010
#> sDRF.4 -5.636 -0.019 -0.122 0.011
#> sDRF.5 -5.515 -0.022 -0.136 0.012
#> sDRF.6 -5.394 -0.026 -0.151 0.013
# DIF
sDIF <- DRF(mod3, Theta_nodes=Theta_nodes, focal_items = 30, draws=200)
car::some(sDIF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.7 -5.273 -0.001 -0.003 0.000
#> sDRF.20 -3.697 -0.004 -0.014 0.000
#> sDRF.22 -3.455 -0.006 -0.018 0.001
#> sDRF.30 -2.485 -0.014 -0.041 0.010
#> sDRF.42 -1.030 0.050 -0.033 0.146
#> sDRF.49 -0.182 0.264 0.143 0.348
#> sDRF.53 0.303 0.314 0.200 0.388
#> sDRF.68 2.121 0.075 0.037 0.126
#> sDRF.78 3.333 0.016 0.005 0.041
#> sDRF.90 4.788 0.002 0.000 0.010
## ----------------------------------------------------------------
# polytomous example
# simulate data where group 2 has a different slopes/intercepts
set.seed(4321)
a1 <- a2 <- matrix(rlnorm(20,.2,.3))
a2[c(16:17, 19:20),] <- a1[c(16:17, 19:20),] + c(-.5, -.25, .25, .5)
# for the graded model, ensure that there is enough space between the intercepts,
# otherwise closer categories will not be selected often
diffs <- t(apply(matrix(runif(20*4, .3, 1), 20), 1, cumsum))
diffs <- -(diffs - rowMeans(diffs))
d1 <- d2 <- diffs + rnorm(20)
rownames(d1) <- rownames(d2) <- paste0('Item.', 1:20)
d2[16:20,] <- d1[16:20,] + matrix(c(-.5, -.5, -.5, -.5,
1, 0, 0, -1,
.5, .5, -.5, -.5,
1, .5, 0, -1,
.5, .5, .5, .5), byrow=TRUE, nrow=5)
tail(data.frame(a.group1 = a1, a.group2 = a2), 6)
#> a.group1 a.group2
#> 15 0.8465935 0.8465935
#> 16 1.9581395 1.4581395
#> 17 1.2486255 0.9986255
#> 18 0.8585293 0.8585293
#> 19 0.7584499 1.0084499
#> 20 0.9760766 1.4760766
list(d.group1 = d1[15:20,], d.group2 = d2[15:20,])
#> $d.group1
#> [,1] [,2] [,3] [,4]
#> Item.15 2.0841033 1.2423287 0.38217647 -0.0009005437
#> Item.16 0.2454193 -0.2924192 -0.63521843 -1.5254133343
#> Item.17 1.3003614 0.5847340 -0.09046573 -0.9841542611
#> Item.18 1.5079114 0.6489106 -0.03799347 -0.3892116221
#> Item.19 1.3766077 0.4483499 -0.20715833 -0.8701328534
#> Item.20 0.1461006 -0.8364834 -1.32963653 -1.6894534436
#>
#> $d.group2
#> [,1] [,2] [,3] [,4]
#> Item.15 2.0841033 1.2423287 0.38217647 -0.0009005437
#> Item.16 -0.2545807 -0.7924192 -1.13521843 -2.0254133343
#> Item.17 2.3003614 0.5847340 -0.09046573 -1.9841542611
#> Item.18 2.0079114 1.1489106 -0.53799347 -0.8892116221
#> Item.19 2.3766077 0.9483499 -0.20715833 -1.8701328534
#> Item.20 0.6461006 -0.3364834 -0.82963653 -1.1894534436
#>
itemtype <- rep('graded', nrow(a1))
N <- 600
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = -.25, sigma = matrix(1.25))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
# item 1-10 as anchors
mod <- multipleGroup(dat, group=group, SE=TRUE,
invariance=c(colnames(dat)[1:10], 'free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $D1
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1.194 0.911 0.177 -0.462 -1.105
#> Item_2 1.320 0.787 0.362 -0.152 -0.951
#> Item_3 1.561 0.794 0.013 -0.973 -1.774
#> Item_4 1.491 1.977 1.304 0.284 -0.236
#> Item_5 1.249 1.435 0.351 -0.329 -1.273
#> Item_6 2.071 0.517 0.072 -0.564 -1.551
#> Item_7 1.333 0.157 -0.374 -0.848 -1.911
#> Item_8 1.304 1.117 0.512 -0.467 -0.868
#> Item_9 1.830 1.501 0.639 -0.176 -0.906
#> Item_10 1.073 1.485 0.567 -0.190 -0.812
#> Item_11 1.327 2.039 1.529 0.756 -0.283
#> Item_12 1.481 -0.268 -1.021 -1.534 -2.229
#> Item_13 0.812 0.641 0.086 -0.832 -1.977
#> Item_14 1.713 1.850 1.191 0.511 -0.262
#> Item_15 0.913 2.168 1.401 0.468 0.058
#> Item_16 2.245 0.286 -0.345 -0.728 -1.687
#> Item_17 1.233 1.357 0.673 0.057 -0.916
#> Item_18 0.983 1.515 0.625 -0.171 -0.564
#> Item_19 0.946 1.415 0.521 -0.227 -0.966
#> Item_20 0.847 0.181 -0.828 -1.245 -1.624
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $D2
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1.194 0.911 0.177 -0.462 -1.105
#> Item_2 1.320 0.787 0.362 -0.152 -0.951
#> Item_3 1.561 0.794 0.013 -0.973 -1.774
#> Item_4 1.491 1.977 1.304 0.284 -0.236
#> Item_5 1.249 1.435 0.351 -0.329 -1.273
#> Item_6 2.071 0.517 0.072 -0.564 -1.551
#> Item_7 1.333 0.157 -0.374 -0.848 -1.911
#> Item_8 1.304 1.117 0.512 -0.467 -0.868
#> Item_9 1.830 1.501 0.639 -0.176 -0.906
#> Item_10 1.073 1.485 0.567 -0.190 -0.812
#> Item_11 1.106 1.818 1.282 0.635 -0.498
#> Item_12 1.562 -0.249 -0.917 -1.667 -2.266
#> Item_13 0.853 0.595 -0.044 -1.057 -1.890
#> Item_14 2.147 2.155 1.311 0.566 -0.248
#> Item_15 0.889 2.101 1.164 0.343 -0.010
#> Item_16 1.622 -0.395 -0.979 -1.278 -2.255
#> Item_17 1.060 2.345 0.587 -0.113 -2.040
#> Item_18 0.923 1.860 1.099 -0.508 -0.793
#> Item_19 1.051 2.528 0.960 -0.227 -1.976
#> Item_20 1.456 0.690 -0.277 -0.806 -1.164
#>
#> $means
#> F1
#> -0.303
#>
#> $cov
#> F1
#> F1 1.147
#>
#>
plot(mod)
# evaluate specific values for sDRF
Theta_nodes <- matrix(seq(-6,6,length.out = 100))
sDTF <- DRF(mod3, Theta_nodes=Theta_nodes, draws=200)
head(sDTF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.1 -6.000 -0.012 -0.087 0.010
#> sDRF.2 -5.879 -0.014 -0.098 0.010
#> sDRF.3 -5.758 -0.016 -0.109 0.010
#> sDRF.4 -5.636 -0.019 -0.122 0.011
#> sDRF.5 -5.515 -0.022 -0.136 0.012
#> sDRF.6 -5.394 -0.026 -0.151 0.013
# DIF
sDIF <- DRF(mod3, Theta_nodes=Theta_nodes, focal_items = 30, draws=200)
car::some(sDIF)
#> Theta sDRF CI_2.5 CI_97.5
#> sDRF.7 -5.273 -0.001 -0.003 0.000
#> sDRF.20 -3.697 -0.004 -0.014 0.000
#> sDRF.22 -3.455 -0.006 -0.018 0.001
#> sDRF.30 -2.485 -0.014 -0.041 0.010
#> sDRF.42 -1.030 0.050 -0.033 0.146
#> sDRF.49 -0.182 0.264 0.143 0.348
#> sDRF.53 0.303 0.314 0.200 0.388
#> sDRF.68 2.121 0.075 0.037 0.126
#> sDRF.78 3.333 0.016 0.005 0.041
#> sDRF.90 4.788 0.002 0.000 0.010
## ----------------------------------------------------------------
# polytomous example
# simulate data where group 2 has a different slopes/intercepts
set.seed(4321)
a1 <- a2 <- matrix(rlnorm(20,.2,.3))
a2[c(16:17, 19:20),] <- a1[c(16:17, 19:20),] + c(-.5, -.25, .25, .5)
# for the graded model, ensure that there is enough space between the intercepts,
# otherwise closer categories will not be selected often
diffs <- t(apply(matrix(runif(20*4, .3, 1), 20), 1, cumsum))
diffs <- -(diffs - rowMeans(diffs))
d1 <- d2 <- diffs + rnorm(20)
rownames(d1) <- rownames(d2) <- paste0('Item.', 1:20)
d2[16:20,] <- d1[16:20,] + matrix(c(-.5, -.5, -.5, -.5,
1, 0, 0, -1,
.5, .5, -.5, -.5,
1, .5, 0, -1,
.5, .5, .5, .5), byrow=TRUE, nrow=5)
tail(data.frame(a.group1 = a1, a.group2 = a2), 6)
#> a.group1 a.group2
#> 15 0.8465935 0.8465935
#> 16 1.9581395 1.4581395
#> 17 1.2486255 0.9986255
#> 18 0.8585293 0.8585293
#> 19 0.7584499 1.0084499
#> 20 0.9760766 1.4760766
list(d.group1 = d1[15:20,], d.group2 = d2[15:20,])
#> $d.group1
#> [,1] [,2] [,3] [,4]
#> Item.15 2.0841033 1.2423287 0.38217647 -0.0009005437
#> Item.16 0.2454193 -0.2924192 -0.63521843 -1.5254133343
#> Item.17 1.3003614 0.5847340 -0.09046573 -0.9841542611
#> Item.18 1.5079114 0.6489106 -0.03799347 -0.3892116221
#> Item.19 1.3766077 0.4483499 -0.20715833 -0.8701328534
#> Item.20 0.1461006 -0.8364834 -1.32963653 -1.6894534436
#>
#> $d.group2
#> [,1] [,2] [,3] [,4]
#> Item.15 2.0841033 1.2423287 0.38217647 -0.0009005437
#> Item.16 -0.2545807 -0.7924192 -1.13521843 -2.0254133343
#> Item.17 2.3003614 0.5847340 -0.09046573 -1.9841542611
#> Item.18 2.0079114 1.1489106 -0.53799347 -0.8892116221
#> Item.19 2.3766077 0.9483499 -0.20715833 -1.8701328534
#> Item.20 0.6461006 -0.3364834 -0.82963653 -1.1894534436
#>
itemtype <- rep('graded', nrow(a1))
N <- 600
dataset1 <- simdata(a1, d1, N, itemtype)
dataset2 <- simdata(a2, d2, N, itemtype, mu = -.25, sigma = matrix(1.25))
dat <- rbind(dataset1, dataset2)
group <- c(rep('D1', N), rep('D2', N))
# item 1-10 as anchors
mod <- multipleGroup(dat, group=group, SE=TRUE,
invariance=c(colnames(dat)[1:10], 'free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $D1
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1.194 0.911 0.177 -0.462 -1.105
#> Item_2 1.320 0.787 0.362 -0.152 -0.951
#> Item_3 1.561 0.794 0.013 -0.973 -1.774
#> Item_4 1.491 1.977 1.304 0.284 -0.236
#> Item_5 1.249 1.435 0.351 -0.329 -1.273
#> Item_6 2.071 0.517 0.072 -0.564 -1.551
#> Item_7 1.333 0.157 -0.374 -0.848 -1.911
#> Item_8 1.304 1.117 0.512 -0.467 -0.868
#> Item_9 1.830 1.501 0.639 -0.176 -0.906
#> Item_10 1.073 1.485 0.567 -0.190 -0.812
#> Item_11 1.327 2.039 1.529 0.756 -0.283
#> Item_12 1.481 -0.268 -1.021 -1.534 -2.229
#> Item_13 0.812 0.641 0.086 -0.832 -1.977
#> Item_14 1.713 1.850 1.191 0.511 -0.262
#> Item_15 0.913 2.168 1.401 0.468 0.058
#> Item_16 2.245 0.286 -0.345 -0.728 -1.687
#> Item_17 1.233 1.357 0.673 0.057 -0.916
#> Item_18 0.983 1.515 0.625 -0.171 -0.564
#> Item_19 0.946 1.415 0.521 -0.227 -0.966
#> Item_20 0.847 0.181 -0.828 -1.245 -1.624
#>
#> $means
#> F1
#> 0
#>
#> $cov
#> F1
#> F1 1
#>
#>
#> $D2
#> $items
#> a1 d1 d2 d3 d4
#> Item_1 1.194 0.911 0.177 -0.462 -1.105
#> Item_2 1.320 0.787 0.362 -0.152 -0.951
#> Item_3 1.561 0.794 0.013 -0.973 -1.774
#> Item_4 1.491 1.977 1.304 0.284 -0.236
#> Item_5 1.249 1.435 0.351 -0.329 -1.273
#> Item_6 2.071 0.517 0.072 -0.564 -1.551
#> Item_7 1.333 0.157 -0.374 -0.848 -1.911
#> Item_8 1.304 1.117 0.512 -0.467 -0.868
#> Item_9 1.830 1.501 0.639 -0.176 -0.906
#> Item_10 1.073 1.485 0.567 -0.190 -0.812
#> Item_11 1.106 1.818 1.282 0.635 -0.498
#> Item_12 1.562 -0.249 -0.917 -1.667 -2.266
#> Item_13 0.853 0.595 -0.044 -1.057 -1.890
#> Item_14 2.147 2.155 1.311 0.566 -0.248
#> Item_15 0.889 2.101 1.164 0.343 -0.010
#> Item_16 1.622 -0.395 -0.979 -1.278 -2.255
#> Item_17 1.060 2.345 0.587 -0.113 -2.040
#> Item_18 0.923 1.860 1.099 -0.508 -0.793
#> Item_19 1.051 2.528 0.960 -0.227 -1.976
#> Item_20 1.456 0.690 -0.277 -0.806 -1.164
#>
#> $means
#> F1
#> -0.303
#>
#> $cov
#> F1
#> F1 1.147
#>
#>
plot(mod)
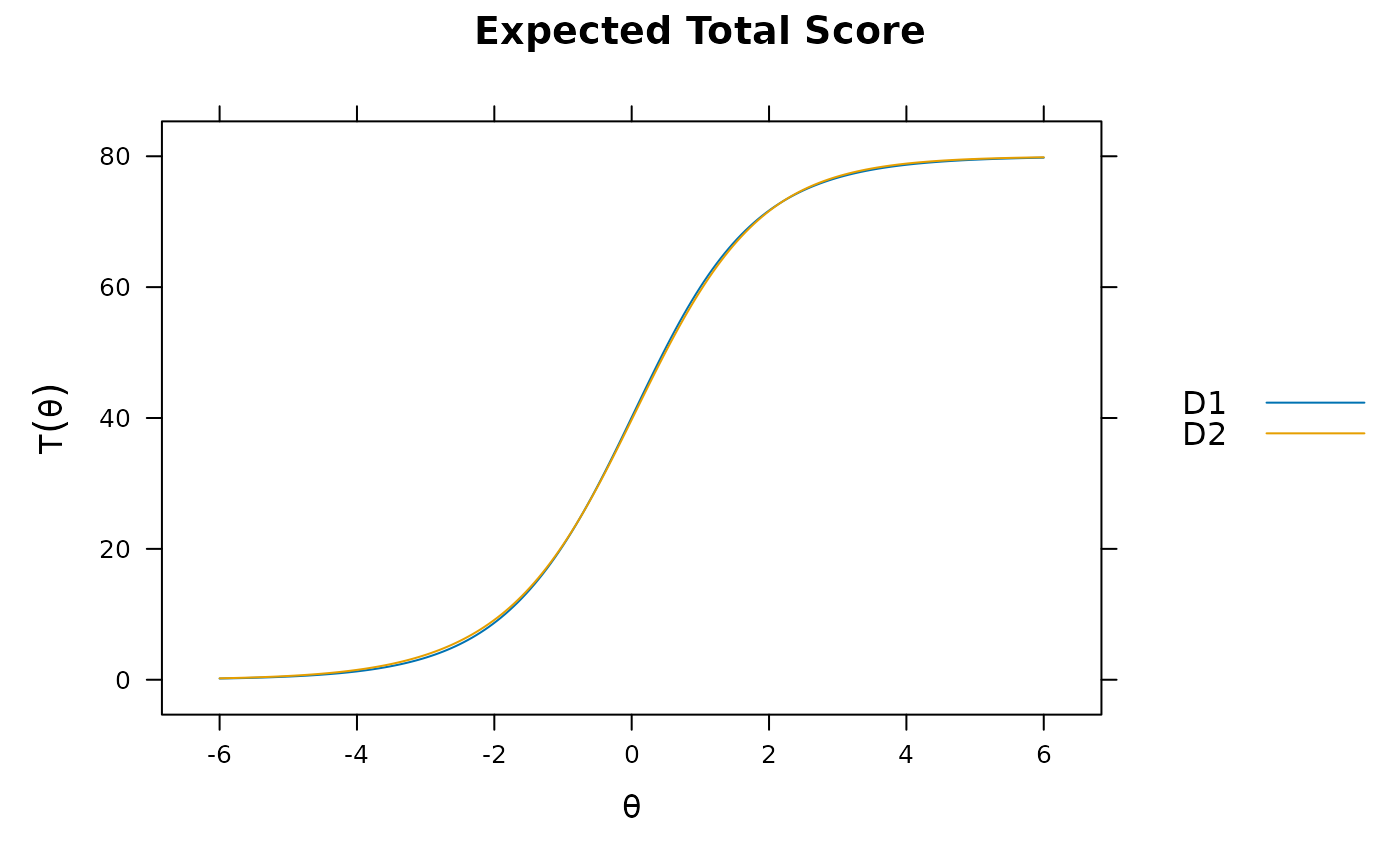 plot(mod, type='itemscore')
plot(mod, type='itemscore')
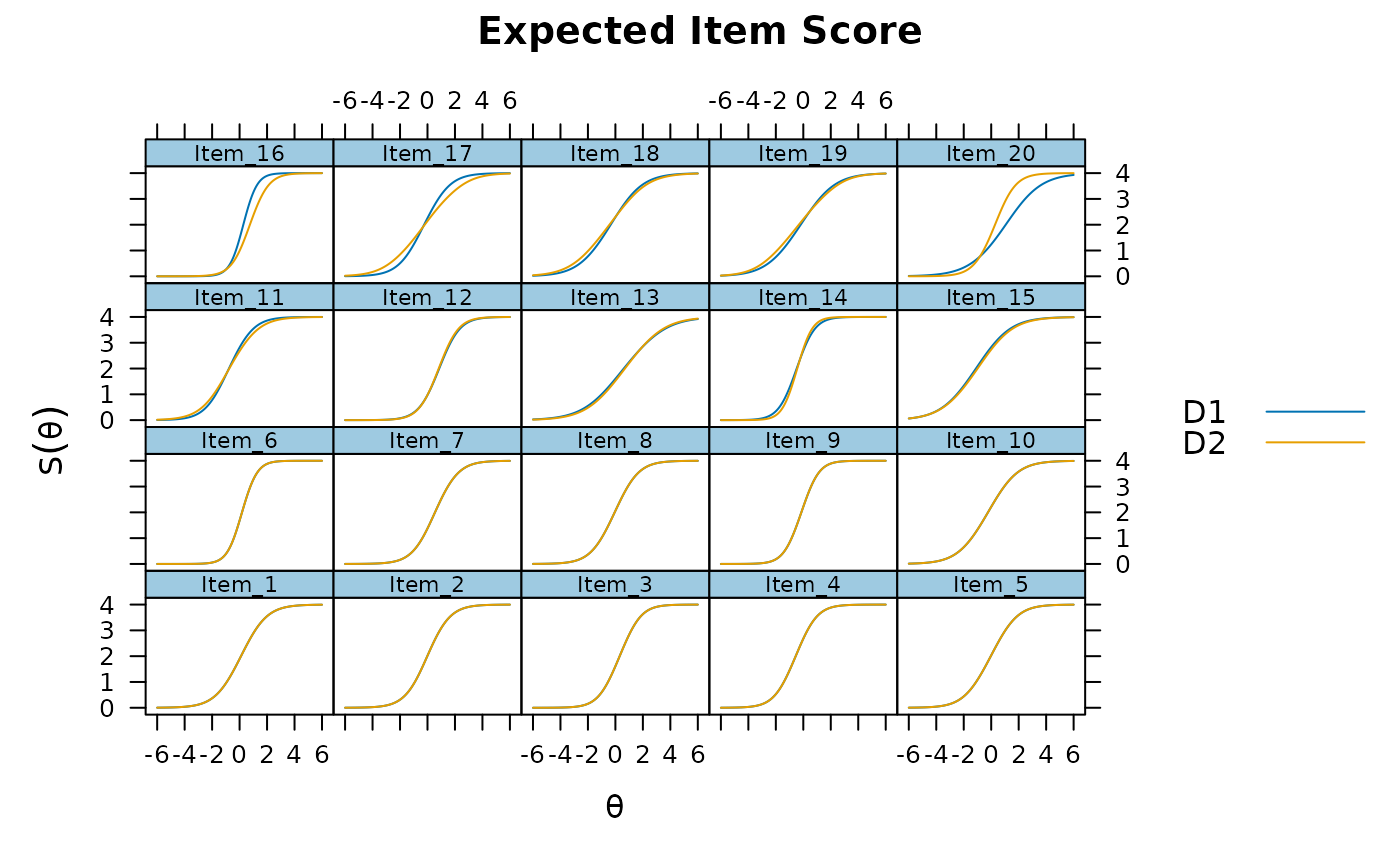 # DIF tests vis Wald method
DIF(mod, items2test=11:20,
which.par=c('a1', paste0('d', 1:4)),
Wald=TRUE, p.adjust='holm')
#> groups W df p adj_p
#> Item_11 D1,D2 5.854 5 0.321 1
#> Item_12 D1,D2 4.808 5 0.44 1
#> Item_13 D1,D2 6.854 5 0.232 1
#> Item_14 D1,D2 4.854 5 0.434 1
#> Item_15 D1,D2 3.861 5 0.57 1
#> Item_16 D1,D2 35.919 5 0 0
#> Item_17 D1,D2 121.671 5 0 0
#> Item_18 D1,D2 45.135 5 0 0
#> Item_19 D1,D2 96.182 5 0 0
#> Item_20 D1,D2 32.769 5 0 0
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 D1,D2 20 -0.195 0.329 0.382
DRF(mod, DIF=TRUE, focal_items=11:20)
#> groups item sDIF uDIF dDIF
#> 1 D1,D2 Item_11 -0.080 0.119 0.131
#> 2 D1,D2 Item_12 0.011 0.024 0.031
#> 3 D1,D2 Item_13 -0.068 0.069 0.072
#> 4 D1,D2 Item_14 -0.010 0.121 0.134
#> 5 D1,D2 Item_15 -0.083 0.083 0.085
#> 6 D1,D2 Item_16 -0.393 0.402 0.522
#> 7 D1,D2 Item_17 -0.053 0.219 0.248
#> 8 D1,D2 Item_18 0.038 0.093 0.110
#> 9 D1,D2 Item_19 0.073 0.104 0.122
#> 10 D1,D2 Item_20 0.370 0.425 0.542
DRF(mod, DIF.cats=TRUE, focal_items=11:20)
#> groups item cat sDIF uDIF dDIF
#> 1 D1,D2 Item_11 1 0.009 0.021 0.024
#> 2 D1,D2 Item_11 2 0.012 0.012 0.012
#> 3 D1,D2 Item_11 3 -0.010 0.015 0.018
#> 4 D1,D2 Item_11 4 0.032 0.032 0.034
#> 5 D1,D2 Item_11 5 -0.041 0.045 0.056
#> 6 D1,D2 Item_12 1 -0.004 0.008 0.010
#> 7 D1,D2 Item_12 2 -0.015 0.015 0.017
#> 8 D1,D2 Item_12 3 0.031 0.031 0.036
#> 9 D1,D2 Item_12 4 -0.013 0.013 0.015
#> 10 D1,D2 Item_12 5 0.001 0.005 0.008
#> 11 D1,D2 Item_13 1 0.012 0.012 0.015
#> 12 D1,D2 Item_13 2 0.017 0.017 0.018
#> 13 D1,D2 Item_13 3 0.010 0.013 0.016
#> 14 D1,D2 Item_13 4 -0.050 0.050 0.053
#> 15 D1,D2 Item_13 5 0.011 0.011 0.016
#> 16 D1,D2 Item_14 1 -0.002 0.028 0.034
#> 17 D1,D2 Item_14 2 0.011 0.018 0.023
#> 18 D1,D2 Item_14 3 -0.004 0.012 0.013
#> 19 D1,D2 Item_14 4 -0.010 0.013 0.015
#> 20 D1,D2 Item_14 5 0.004 0.034 0.037
#> 21 D1,D2 Item_15 1 0.006 0.006 0.006
#> 22 D1,D2 Item_15 2 0.033 0.033 0.034
#> 23 D1,D2 Item_15 3 -0.014 0.014 0.018
#> 24 D1,D2 Item_15 4 -0.011 0.011 0.012
#> 25 D1,D2 Item_15 5 -0.014 0.014 0.015
#> 26 D1,D2 Item_16 1 0.099 0.103 0.126
#> 27 D1,D2 Item_16 2 0.004 0.025 0.031
#> 28 D1,D2 Item_16 3 -0.008 0.017 0.021
#> 29 D1,D2 Item_16 4 -0.001 0.033 0.047
#> 30 D1,D2 Item_16 5 -0.095 0.095 0.144
#> 31 D1,D2 Item_17 1 -0.147 0.147 0.175
#> 32 D1,D2 Item_17 2 0.154 0.154 0.170
#> 33 D1,D2 Item_17 3 0.024 0.024 0.024
#> 34 D1,D2 Item_17 4 0.132 0.132 0.152
#> 35 D1,D2 Item_17 5 -0.162 0.162 0.191
#> 36 D1,D2 Item_18 1 -0.055 0.055 0.064
#> 37 D1,D2 Item_18 2 -0.039 0.040 0.043
#> 38 D1,D2 Item_18 3 0.162 0.162 0.164
#> 39 D1,D2 Item_18 4 -0.023 0.023 0.024
#> 40 D1,D2 Item_18 5 -0.044 0.044 0.049
#> 41 D1,D2 Item_19 1 -0.133 0.133 0.145
#> 42 D1,D2 Item_19 2 0.054 0.059 0.083
#> 43 D1,D2 Item_19 3 0.078 0.078 0.083
#> 44 D1,D2 Item_19 4 0.137 0.137 0.155
#> 45 D1,D2 Item_19 5 -0.138 0.138 0.149
#> 46 D1,D2 Item_20 1 -0.072 0.098 0.110
#> 47 D1,D2 Item_20 2 -0.038 0.040 0.056
#> 48 D1,D2 Item_20 3 0.016 0.024 0.028
#> 49 D1,D2 Item_20 4 0.000 0.011 0.015
#> 50 D1,D2 Item_20 5 0.095 0.102 0.146
## ----------------------------------------------------------------
### multidimensional DTF
set.seed(1234)
n <- 50
N <- 1000
# only first 5 items as anchors within each dimension
model <- 'F1 = 1-25
F2 = 26-50
COV = F1*F2
CONSTRAINB = (1-5, a1), (1-5, 26-30, d), (26-30, a2)'
a <- matrix(c(rep(1, 25), numeric(50), rep(1, 25)), n)
d <- matrix(rnorm(n), n)
group <- c(rep('Group_1', N), rep('Group_2', N))
Cov <- matrix(c(1, .5, .5, 1.5), 2)
Mean <- c(0, 0.5)
# groups completely equal
dat1 <- simdata(a, d, N, itemtype = 'dich', sigma = cov2cor(Cov))
dat2 <- simdata(a, d, N, itemtype = 'dich', sigma = Cov, mu = Mean)
dat <- rbind(dat1, dat2)
mod <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $Group_1
#> $items
#> a1 a2 d g u
#> Item_1 1.006 0.000 -1.208 0 1
#> Item_2 1.080 0.000 0.301 0 1
#> Item_3 0.833 0.000 1.126 0 1
#> Item_4 0.977 0.000 -2.342 0 1
#> Item_5 1.005 0.000 0.410 0 1
#> Item_6 0.864 0.000 0.428 0 1
#> Item_7 1.014 0.000 -0.495 0 1
#> Item_8 1.133 0.000 -0.472 0 1
#> Item_9 0.945 0.000 -0.585 0 1
#> Item_10 1.001 0.000 -0.787 0 1
#> Item_11 1.009 0.000 -0.390 0 1
#> Item_12 0.920 0.000 -1.061 0 1
#> Item_13 1.189 0.000 -0.711 0 1
#> Item_14 1.125 0.000 0.066 0 1
#> Item_15 1.122 0.000 0.896 0 1
#> Item_16 1.094 0.000 -0.203 0 1
#> Item_17 1.041 0.000 -0.479 0 1
#> Item_18 1.011 0.000 -0.849 0 1
#> Item_19 0.962 0.000 -0.768 0 1
#> Item_20 0.937 0.000 2.372 0 1
#> Item_21 0.935 0.000 0.082 0 1
#> Item_22 0.886 0.000 -0.482 0 1
#> Item_23 0.921 0.000 -0.443 0 1
#> Item_24 0.937 0.000 0.521 0 1
#> Item_25 0.959 0.000 -0.674 0 1
#> Item_26 0.000 0.999 -1.498 0 1
#> Item_27 0.000 0.978 0.590 0 1
#> Item_28 0.000 0.997 -1.035 0 1
#> Item_29 0.000 0.917 -0.055 0 1
#> Item_30 0.000 0.982 -0.970 0 1
#> Item_31 0.000 0.891 0.931 0 1
#> Item_32 0.000 0.863 -0.453 0 1
#> Item_33 0.000 1.140 -0.759 0 1
#> Item_34 0.000 0.943 -0.469 0 1
#> Item_35 0.000 1.289 -1.852 0 1
#> Item_36 0.000 0.791 -1.064 0 1
#> Item_37 0.000 0.980 -2.323 0 1
#> Item_38 0.000 1.051 -1.367 0 1
#> Item_39 0.000 1.097 -0.113 0 1
#> Item_40 0.000 0.908 -0.523 0 1
#> Item_41 0.000 1.059 1.708 0 1
#> Item_42 0.000 1.146 -1.078 0 1
#> Item_43 0.000 1.086 -0.967 0 1
#> Item_44 0.000 1.095 -0.415 0 1
#> Item_45 0.000 0.984 -1.066 0 1
#> Item_46 0.000 0.996 -0.726 0 1
#> Item_47 0.000 1.330 -1.037 0 1
#> Item_48 0.000 1.072 -1.148 0 1
#> Item_49 0.000 0.898 -0.429 0 1
#> Item_50 0.000 1.078 -0.525 0 1
#>
#> $means
#> F1 F2
#> 0 0
#>
#> $cov
#> F1 F2
#> F1 1.000 0.453
#> F2 0.453 1.000
#>
#>
#> $Group_2
#> $items
#> a1 a2 d g u
#> Item_1 1.006 0.000 -1.208 0 1
#> Item_2 1.080 0.000 0.301 0 1
#> Item_3 0.833 0.000 1.126 0 1
#> Item_4 0.977 0.000 -2.342 0 1
#> Item_5 1.005 0.000 0.410 0 1
#> Item_6 0.886 0.000 0.558 0 1
#> Item_7 0.967 0.000 -0.583 0 1
#> Item_8 0.988 0.000 -0.613 0 1
#> Item_9 0.962 0.000 -0.467 0 1
#> Item_10 0.865 0.000 -0.999 0 1
#> Item_11 1.076 0.000 -0.448 0 1
#> Item_12 1.145 0.000 -1.198 0 1
#> Item_13 0.991 0.000 -0.789 0 1
#> Item_14 1.039 0.000 0.070 0 1
#> Item_15 1.201 0.000 1.070 0 1
#> Item_16 0.989 0.000 -0.084 0 1
#> Item_17 0.995 0.000 -0.569 0 1
#> Item_18 0.932 0.000 -0.925 0 1
#> Item_19 0.866 0.000 -0.790 0 1
#> Item_20 1.123 0.000 2.463 0 1
#> Item_21 1.055 0.000 0.200 0 1
#> Item_22 1.107 0.000 -0.610 0 1
#> Item_23 0.992 0.000 -0.513 0 1
#> Item_24 0.992 0.000 0.388 0 1
#> Item_25 0.934 0.000 -0.794 0 1
#> Item_26 0.000 0.999 -1.498 0 1
#> Item_27 0.000 0.978 0.590 0 1
#> Item_28 0.000 0.997 -1.035 0 1
#> Item_29 0.000 0.917 -0.055 0 1
#> Item_30 0.000 0.982 -0.970 0 1
#> Item_31 0.000 1.015 0.962 0 1
#> Item_32 0.000 1.115 -0.596 0 1
#> Item_33 0.000 1.095 -0.874 0 1
#> Item_34 0.000 0.856 -0.486 0 1
#> Item_35 0.000 1.138 -1.636 0 1
#> Item_36 0.000 1.085 -1.353 0 1
#> Item_37 0.000 1.115 -2.169 0 1
#> Item_38 0.000 1.146 -1.450 0 1
#> Item_39 0.000 1.130 -0.441 0 1
#> Item_40 0.000 0.978 -0.632 0 1
#> Item_41 0.000 1.202 1.439 0 1
#> Item_42 0.000 0.942 -0.943 0 1
#> Item_43 0.000 1.033 -0.899 0 1
#> Item_44 0.000 1.144 -0.339 0 1
#> Item_45 0.000 0.844 -0.728 0 1
#> Item_46 0.000 1.068 -1.046 0 1
#> Item_47 0.000 0.952 -1.123 0 1
#> Item_48 0.000 1.018 -1.317 0 1
#> Item_49 0.000 0.881 -0.381 0 1
#> Item_50 0.000 1.092 -0.605 0 1
#>
#> $means
#> F1 F2
#> 0.072 0.505
#>
#> $cov
#> F1 F2
#> F1 1.067 0.518
#> F2 0.518 1.415
#>
#>
plot(mod, degrees = c(45,45))
# DIF tests vis Wald method
DIF(mod, items2test=11:20,
which.par=c('a1', paste0('d', 1:4)),
Wald=TRUE, p.adjust='holm')
#> groups W df p adj_p
#> Item_11 D1,D2 5.854 5 0.321 1
#> Item_12 D1,D2 4.808 5 0.44 1
#> Item_13 D1,D2 6.854 5 0.232 1
#> Item_14 D1,D2 4.854 5 0.434 1
#> Item_15 D1,D2 3.861 5 0.57 1
#> Item_16 D1,D2 35.919 5 0 0
#> Item_17 D1,D2 121.671 5 0 0
#> Item_18 D1,D2 45.135 5 0 0
#> Item_19 D1,D2 96.182 5 0 0
#> Item_20 D1,D2 32.769 5 0 0
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 D1,D2 20 -0.195 0.329 0.382
DRF(mod, DIF=TRUE, focal_items=11:20)
#> groups item sDIF uDIF dDIF
#> 1 D1,D2 Item_11 -0.080 0.119 0.131
#> 2 D1,D2 Item_12 0.011 0.024 0.031
#> 3 D1,D2 Item_13 -0.068 0.069 0.072
#> 4 D1,D2 Item_14 -0.010 0.121 0.134
#> 5 D1,D2 Item_15 -0.083 0.083 0.085
#> 6 D1,D2 Item_16 -0.393 0.402 0.522
#> 7 D1,D2 Item_17 -0.053 0.219 0.248
#> 8 D1,D2 Item_18 0.038 0.093 0.110
#> 9 D1,D2 Item_19 0.073 0.104 0.122
#> 10 D1,D2 Item_20 0.370 0.425 0.542
DRF(mod, DIF.cats=TRUE, focal_items=11:20)
#> groups item cat sDIF uDIF dDIF
#> 1 D1,D2 Item_11 1 0.009 0.021 0.024
#> 2 D1,D2 Item_11 2 0.012 0.012 0.012
#> 3 D1,D2 Item_11 3 -0.010 0.015 0.018
#> 4 D1,D2 Item_11 4 0.032 0.032 0.034
#> 5 D1,D2 Item_11 5 -0.041 0.045 0.056
#> 6 D1,D2 Item_12 1 -0.004 0.008 0.010
#> 7 D1,D2 Item_12 2 -0.015 0.015 0.017
#> 8 D1,D2 Item_12 3 0.031 0.031 0.036
#> 9 D1,D2 Item_12 4 -0.013 0.013 0.015
#> 10 D1,D2 Item_12 5 0.001 0.005 0.008
#> 11 D1,D2 Item_13 1 0.012 0.012 0.015
#> 12 D1,D2 Item_13 2 0.017 0.017 0.018
#> 13 D1,D2 Item_13 3 0.010 0.013 0.016
#> 14 D1,D2 Item_13 4 -0.050 0.050 0.053
#> 15 D1,D2 Item_13 5 0.011 0.011 0.016
#> 16 D1,D2 Item_14 1 -0.002 0.028 0.034
#> 17 D1,D2 Item_14 2 0.011 0.018 0.023
#> 18 D1,D2 Item_14 3 -0.004 0.012 0.013
#> 19 D1,D2 Item_14 4 -0.010 0.013 0.015
#> 20 D1,D2 Item_14 5 0.004 0.034 0.037
#> 21 D1,D2 Item_15 1 0.006 0.006 0.006
#> 22 D1,D2 Item_15 2 0.033 0.033 0.034
#> 23 D1,D2 Item_15 3 -0.014 0.014 0.018
#> 24 D1,D2 Item_15 4 -0.011 0.011 0.012
#> 25 D1,D2 Item_15 5 -0.014 0.014 0.015
#> 26 D1,D2 Item_16 1 0.099 0.103 0.126
#> 27 D1,D2 Item_16 2 0.004 0.025 0.031
#> 28 D1,D2 Item_16 3 -0.008 0.017 0.021
#> 29 D1,D2 Item_16 4 -0.001 0.033 0.047
#> 30 D1,D2 Item_16 5 -0.095 0.095 0.144
#> 31 D1,D2 Item_17 1 -0.147 0.147 0.175
#> 32 D1,D2 Item_17 2 0.154 0.154 0.170
#> 33 D1,D2 Item_17 3 0.024 0.024 0.024
#> 34 D1,D2 Item_17 4 0.132 0.132 0.152
#> 35 D1,D2 Item_17 5 -0.162 0.162 0.191
#> 36 D1,D2 Item_18 1 -0.055 0.055 0.064
#> 37 D1,D2 Item_18 2 -0.039 0.040 0.043
#> 38 D1,D2 Item_18 3 0.162 0.162 0.164
#> 39 D1,D2 Item_18 4 -0.023 0.023 0.024
#> 40 D1,D2 Item_18 5 -0.044 0.044 0.049
#> 41 D1,D2 Item_19 1 -0.133 0.133 0.145
#> 42 D1,D2 Item_19 2 0.054 0.059 0.083
#> 43 D1,D2 Item_19 3 0.078 0.078 0.083
#> 44 D1,D2 Item_19 4 0.137 0.137 0.155
#> 45 D1,D2 Item_19 5 -0.138 0.138 0.149
#> 46 D1,D2 Item_20 1 -0.072 0.098 0.110
#> 47 D1,D2 Item_20 2 -0.038 0.040 0.056
#> 48 D1,D2 Item_20 3 0.016 0.024 0.028
#> 49 D1,D2 Item_20 4 0.000 0.011 0.015
#> 50 D1,D2 Item_20 5 0.095 0.102 0.146
## ----------------------------------------------------------------
### multidimensional DTF
set.seed(1234)
n <- 50
N <- 1000
# only first 5 items as anchors within each dimension
model <- 'F1 = 1-25
F2 = 26-50
COV = F1*F2
CONSTRAINB = (1-5, a1), (1-5, 26-30, d), (26-30, a2)'
a <- matrix(c(rep(1, 25), numeric(50), rep(1, 25)), n)
d <- matrix(rnorm(n), n)
group <- c(rep('Group_1', N), rep('Group_2', N))
Cov <- matrix(c(1, .5, .5, 1.5), 2)
Mean <- c(0, 0.5)
# groups completely equal
dat1 <- simdata(a, d, N, itemtype = 'dich', sigma = cov2cor(Cov))
dat2 <- simdata(a, d, N, itemtype = 'dich', sigma = Cov, mu = Mean)
dat <- rbind(dat1, dat2)
mod <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $Group_1
#> $items
#> a1 a2 d g u
#> Item_1 1.006 0.000 -1.208 0 1
#> Item_2 1.080 0.000 0.301 0 1
#> Item_3 0.833 0.000 1.126 0 1
#> Item_4 0.977 0.000 -2.342 0 1
#> Item_5 1.005 0.000 0.410 0 1
#> Item_6 0.864 0.000 0.428 0 1
#> Item_7 1.014 0.000 -0.495 0 1
#> Item_8 1.133 0.000 -0.472 0 1
#> Item_9 0.945 0.000 -0.585 0 1
#> Item_10 1.001 0.000 -0.787 0 1
#> Item_11 1.009 0.000 -0.390 0 1
#> Item_12 0.920 0.000 -1.061 0 1
#> Item_13 1.189 0.000 -0.711 0 1
#> Item_14 1.125 0.000 0.066 0 1
#> Item_15 1.122 0.000 0.896 0 1
#> Item_16 1.094 0.000 -0.203 0 1
#> Item_17 1.041 0.000 -0.479 0 1
#> Item_18 1.011 0.000 -0.849 0 1
#> Item_19 0.962 0.000 -0.768 0 1
#> Item_20 0.937 0.000 2.372 0 1
#> Item_21 0.935 0.000 0.082 0 1
#> Item_22 0.886 0.000 -0.482 0 1
#> Item_23 0.921 0.000 -0.443 0 1
#> Item_24 0.937 0.000 0.521 0 1
#> Item_25 0.959 0.000 -0.674 0 1
#> Item_26 0.000 0.999 -1.498 0 1
#> Item_27 0.000 0.978 0.590 0 1
#> Item_28 0.000 0.997 -1.035 0 1
#> Item_29 0.000 0.917 -0.055 0 1
#> Item_30 0.000 0.982 -0.970 0 1
#> Item_31 0.000 0.891 0.931 0 1
#> Item_32 0.000 0.863 -0.453 0 1
#> Item_33 0.000 1.140 -0.759 0 1
#> Item_34 0.000 0.943 -0.469 0 1
#> Item_35 0.000 1.289 -1.852 0 1
#> Item_36 0.000 0.791 -1.064 0 1
#> Item_37 0.000 0.980 -2.323 0 1
#> Item_38 0.000 1.051 -1.367 0 1
#> Item_39 0.000 1.097 -0.113 0 1
#> Item_40 0.000 0.908 -0.523 0 1
#> Item_41 0.000 1.059 1.708 0 1
#> Item_42 0.000 1.146 -1.078 0 1
#> Item_43 0.000 1.086 -0.967 0 1
#> Item_44 0.000 1.095 -0.415 0 1
#> Item_45 0.000 0.984 -1.066 0 1
#> Item_46 0.000 0.996 -0.726 0 1
#> Item_47 0.000 1.330 -1.037 0 1
#> Item_48 0.000 1.072 -1.148 0 1
#> Item_49 0.000 0.898 -0.429 0 1
#> Item_50 0.000 1.078 -0.525 0 1
#>
#> $means
#> F1 F2
#> 0 0
#>
#> $cov
#> F1 F2
#> F1 1.000 0.453
#> F2 0.453 1.000
#>
#>
#> $Group_2
#> $items
#> a1 a2 d g u
#> Item_1 1.006 0.000 -1.208 0 1
#> Item_2 1.080 0.000 0.301 0 1
#> Item_3 0.833 0.000 1.126 0 1
#> Item_4 0.977 0.000 -2.342 0 1
#> Item_5 1.005 0.000 0.410 0 1
#> Item_6 0.886 0.000 0.558 0 1
#> Item_7 0.967 0.000 -0.583 0 1
#> Item_8 0.988 0.000 -0.613 0 1
#> Item_9 0.962 0.000 -0.467 0 1
#> Item_10 0.865 0.000 -0.999 0 1
#> Item_11 1.076 0.000 -0.448 0 1
#> Item_12 1.145 0.000 -1.198 0 1
#> Item_13 0.991 0.000 -0.789 0 1
#> Item_14 1.039 0.000 0.070 0 1
#> Item_15 1.201 0.000 1.070 0 1
#> Item_16 0.989 0.000 -0.084 0 1
#> Item_17 0.995 0.000 -0.569 0 1
#> Item_18 0.932 0.000 -0.925 0 1
#> Item_19 0.866 0.000 -0.790 0 1
#> Item_20 1.123 0.000 2.463 0 1
#> Item_21 1.055 0.000 0.200 0 1
#> Item_22 1.107 0.000 -0.610 0 1
#> Item_23 0.992 0.000 -0.513 0 1
#> Item_24 0.992 0.000 0.388 0 1
#> Item_25 0.934 0.000 -0.794 0 1
#> Item_26 0.000 0.999 -1.498 0 1
#> Item_27 0.000 0.978 0.590 0 1
#> Item_28 0.000 0.997 -1.035 0 1
#> Item_29 0.000 0.917 -0.055 0 1
#> Item_30 0.000 0.982 -0.970 0 1
#> Item_31 0.000 1.015 0.962 0 1
#> Item_32 0.000 1.115 -0.596 0 1
#> Item_33 0.000 1.095 -0.874 0 1
#> Item_34 0.000 0.856 -0.486 0 1
#> Item_35 0.000 1.138 -1.636 0 1
#> Item_36 0.000 1.085 -1.353 0 1
#> Item_37 0.000 1.115 -2.169 0 1
#> Item_38 0.000 1.146 -1.450 0 1
#> Item_39 0.000 1.130 -0.441 0 1
#> Item_40 0.000 0.978 -0.632 0 1
#> Item_41 0.000 1.202 1.439 0 1
#> Item_42 0.000 0.942 -0.943 0 1
#> Item_43 0.000 1.033 -0.899 0 1
#> Item_44 0.000 1.144 -0.339 0 1
#> Item_45 0.000 0.844 -0.728 0 1
#> Item_46 0.000 1.068 -1.046 0 1
#> Item_47 0.000 0.952 -1.123 0 1
#> Item_48 0.000 1.018 -1.317 0 1
#> Item_49 0.000 0.881 -0.381 0 1
#> Item_50 0.000 1.092 -0.605 0 1
#>
#> $means
#> F1 F2
#> 0.072 0.505
#>
#> $cov
#> F1 F2
#> F1 1.067 0.518
#> F2 0.518 1.415
#>
#>
plot(mod, degrees = c(45,45))
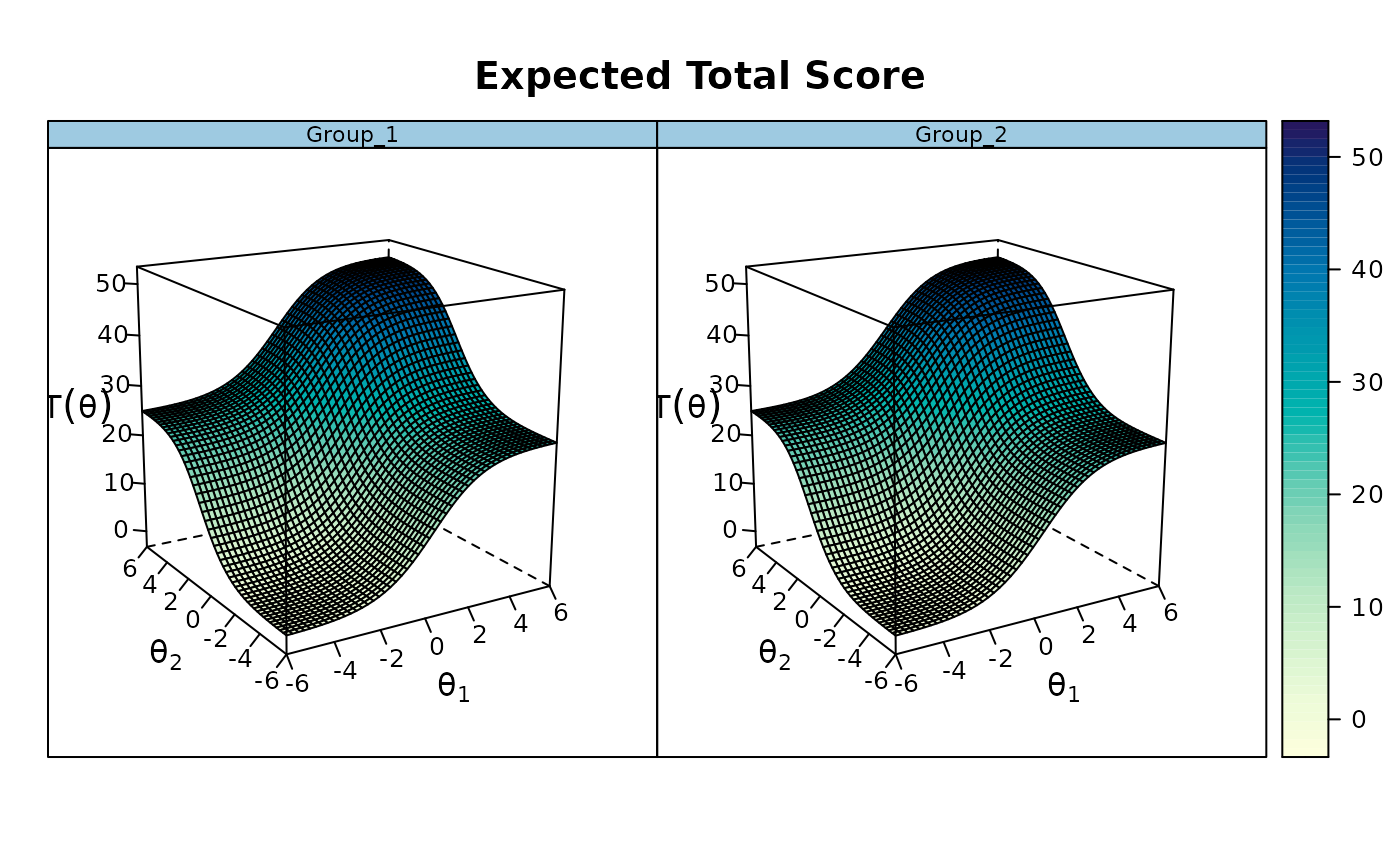 DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 50 -0.347 0.347 0.353
# some intercepts slightly higher in Group 2
d2 <- d
d2[c(10:15, 31:35)] <- d2[c(10:15, 31:35)] + 1
dat1 <- simdata(a, d, N, itemtype = 'dich', sigma = cov2cor(Cov))
dat2 <- simdata(a, d2, N, itemtype = 'dich', sigma = Cov, mu = Mean)
dat <- rbind(dat1, dat2)
mod <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $Group_1
#> $items
#> a1 a2 d g u
#> Item_1 0.942 0.000 -1.195 0 1
#> Item_2 0.973 0.000 0.294 0 1
#> Item_3 0.833 0.000 1.131 0 1
#> Item_4 1.049 0.000 -2.575 0 1
#> Item_5 1.078 0.000 0.517 0 1
#> Item_6 0.919 0.000 0.456 0 1
#> Item_7 0.929 0.000 -0.473 0 1
#> Item_8 0.918 0.000 -0.554 0 1
#> Item_9 0.907 0.000 -0.582 0 1
#> Item_10 1.096 0.000 -0.821 0 1
#> Item_11 1.000 0.000 -0.483 0 1
#> Item_12 0.986 0.000 -1.016 0 1
#> Item_13 1.013 0.000 -0.870 0 1
#> Item_14 0.861 0.000 0.104 0 1
#> Item_15 1.097 0.000 0.908 0 1
#> Item_16 0.871 0.000 -0.119 0 1
#> Item_17 0.949 0.000 -0.417 0 1
#> Item_18 1.019 0.000 -0.987 0 1
#> Item_19 1.031 0.000 -0.962 0 1
#> Item_20 0.904 0.000 2.378 0 1
#> Item_21 1.177 0.000 0.061 0 1
#> Item_22 1.044 0.000 -0.551 0 1
#> Item_23 0.948 0.000 -0.510 0 1
#> Item_24 0.915 0.000 0.387 0 1
#> Item_25 0.901 0.000 -0.778 0 1
#> Item_26 0.000 0.979 -1.450 0 1
#> Item_27 0.000 0.999 0.603 0 1
#> Item_28 0.000 1.105 -1.108 0 1
#> Item_29 0.000 1.034 0.043 0 1
#> Item_30 0.000 0.974 -0.925 0 1
#> Item_31 0.000 0.982 1.258 0 1
#> Item_32 0.000 1.012 -0.407 0 1
#> Item_33 0.000 0.957 -0.619 0 1
#> Item_34 0.000 1.076 -0.548 0 1
#> Item_35 0.000 0.761 -1.608 0 1
#> Item_36 0.000 0.962 -1.091 0 1
#> Item_37 0.000 0.891 -2.076 0 1
#> Item_38 0.000 0.895 -1.162 0 1
#> Item_39 0.000 1.023 -0.260 0 1
#> Item_40 0.000 0.949 -0.394 0 1
#> Item_41 0.000 1.145 1.451 0 1
#> Item_42 0.000 1.037 -1.063 0 1
#> Item_43 0.000 0.891 -0.937 0 1
#> Item_44 0.000 0.929 -0.397 0 1
#> Item_45 0.000 0.987 -0.887 0 1
#> Item_46 0.000 0.955 -1.032 0 1
#> Item_47 0.000 0.888 -1.063 0 1
#> Item_48 0.000 1.058 -1.267 0 1
#> Item_49 0.000 0.969 -0.486 0 1
#> Item_50 0.000 1.086 -0.442 0 1
#>
#> $means
#> F1 F2
#> 0 0
#>
#> $cov
#> F1 F2
#> F1 1.000 0.409
#> F2 0.409 1.000
#>
#>
#> $Group_2
#> $items
#> a1 a2 d g u
#> Item_1 0.942 0.000 -1.195 0 1
#> Item_2 0.973 0.000 0.294 0 1
#> Item_3 0.833 0.000 1.131 0 1
#> Item_4 1.049 0.000 -2.575 0 1
#> Item_5 1.078 0.000 0.517 0 1
#> Item_6 0.903 0.000 0.610 0 1
#> Item_7 1.006 0.000 -0.476 0 1
#> Item_8 0.889 0.000 -0.501 0 1
#> Item_9 0.855 0.000 -0.604 0 1
#> Item_10 0.892 0.000 0.069 0 1
#> Item_11 0.931 0.000 0.498 0 1
#> Item_12 0.962 0.000 0.065 0 1
#> Item_13 0.845 0.000 0.311 0 1
#> Item_14 0.893 0.000 1.036 0 1
#> Item_15 0.998 0.000 1.919 0 1
#> Item_16 0.949 0.000 -0.155 0 1
#> Item_17 0.989 0.000 -0.545 0 1
#> Item_18 0.866 0.000 -0.945 0 1
#> Item_19 0.893 0.000 -0.872 0 1
#> Item_20 0.732 0.000 2.195 0 1
#> Item_21 0.854 0.000 0.059 0 1
#> Item_22 0.783 0.000 -0.498 0 1
#> Item_23 0.966 0.000 -0.561 0 1
#> Item_24 0.944 0.000 0.384 0 1
#> Item_25 0.940 0.000 -0.794 0 1
#> Item_26 0.000 0.979 -1.450 0 1
#> Item_27 0.000 0.999 0.603 0 1
#> Item_28 0.000 1.105 -1.108 0 1
#> Item_29 0.000 1.034 0.043 0 1
#> Item_30 0.000 0.974 -0.925 0 1
#> Item_31 0.000 0.998 1.989 0 1
#> Item_32 0.000 1.190 0.252 0 1
#> Item_33 0.000 1.064 0.076 0 1
#> Item_34 0.000 0.885 0.444 0 1
#> Item_35 0.000 1.065 -0.597 0 1
#> Item_36 0.000 1.080 -1.273 0 1
#> Item_37 0.000 1.034 -2.217 0 1
#> Item_38 0.000 1.040 -1.451 0 1
#> Item_39 0.000 1.160 -0.496 0 1
#> Item_40 0.000 1.015 -0.711 0 1
#> Item_41 0.000 0.946 1.416 0 1
#> Item_42 0.000 1.006 -1.144 0 1
#> Item_43 0.000 0.969 -0.818 0 1
#> Item_44 0.000 1.099 -0.322 0 1
#> Item_45 0.000 1.062 -1.103 0 1
#> Item_46 0.000 1.064 -0.951 0 1
#> Item_47 0.000 1.025 -1.122 0 1
#> Item_48 0.000 0.975 -1.194 0 1
#> Item_49 0.000 1.083 -0.461 0 1
#> Item_50 0.000 0.935 -0.512 0 1
#>
#> $means
#> F1 F2
#> 0.003 0.578
#>
#> $cov
#> F1 F2
#> F1 1.165 0.459
#> F2 0.459 1.340
#>
#>
plot(mod, degrees = c(45,45))
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 50 -0.347 0.347 0.353
# some intercepts slightly higher in Group 2
d2 <- d
d2[c(10:15, 31:35)] <- d2[c(10:15, 31:35)] + 1
dat1 <- simdata(a, d, N, itemtype = 'dich', sigma = cov2cor(Cov))
dat2 <- simdata(a, d2, N, itemtype = 'dich', sigma = Cov, mu = Mean)
dat <- rbind(dat1, dat2)
mod <- multipleGroup(dat, model, group=group, SE=TRUE,
invariance=c('free_means', 'free_var'))
coef(mod, simplify=TRUE)
#> $Group_1
#> $items
#> a1 a2 d g u
#> Item_1 0.942 0.000 -1.195 0 1
#> Item_2 0.973 0.000 0.294 0 1
#> Item_3 0.833 0.000 1.131 0 1
#> Item_4 1.049 0.000 -2.575 0 1
#> Item_5 1.078 0.000 0.517 0 1
#> Item_6 0.919 0.000 0.456 0 1
#> Item_7 0.929 0.000 -0.473 0 1
#> Item_8 0.918 0.000 -0.554 0 1
#> Item_9 0.907 0.000 -0.582 0 1
#> Item_10 1.096 0.000 -0.821 0 1
#> Item_11 1.000 0.000 -0.483 0 1
#> Item_12 0.986 0.000 -1.016 0 1
#> Item_13 1.013 0.000 -0.870 0 1
#> Item_14 0.861 0.000 0.104 0 1
#> Item_15 1.097 0.000 0.908 0 1
#> Item_16 0.871 0.000 -0.119 0 1
#> Item_17 0.949 0.000 -0.417 0 1
#> Item_18 1.019 0.000 -0.987 0 1
#> Item_19 1.031 0.000 -0.962 0 1
#> Item_20 0.904 0.000 2.378 0 1
#> Item_21 1.177 0.000 0.061 0 1
#> Item_22 1.044 0.000 -0.551 0 1
#> Item_23 0.948 0.000 -0.510 0 1
#> Item_24 0.915 0.000 0.387 0 1
#> Item_25 0.901 0.000 -0.778 0 1
#> Item_26 0.000 0.979 -1.450 0 1
#> Item_27 0.000 0.999 0.603 0 1
#> Item_28 0.000 1.105 -1.108 0 1
#> Item_29 0.000 1.034 0.043 0 1
#> Item_30 0.000 0.974 -0.925 0 1
#> Item_31 0.000 0.982 1.258 0 1
#> Item_32 0.000 1.012 -0.407 0 1
#> Item_33 0.000 0.957 -0.619 0 1
#> Item_34 0.000 1.076 -0.548 0 1
#> Item_35 0.000 0.761 -1.608 0 1
#> Item_36 0.000 0.962 -1.091 0 1
#> Item_37 0.000 0.891 -2.076 0 1
#> Item_38 0.000 0.895 -1.162 0 1
#> Item_39 0.000 1.023 -0.260 0 1
#> Item_40 0.000 0.949 -0.394 0 1
#> Item_41 0.000 1.145 1.451 0 1
#> Item_42 0.000 1.037 -1.063 0 1
#> Item_43 0.000 0.891 -0.937 0 1
#> Item_44 0.000 0.929 -0.397 0 1
#> Item_45 0.000 0.987 -0.887 0 1
#> Item_46 0.000 0.955 -1.032 0 1
#> Item_47 0.000 0.888 -1.063 0 1
#> Item_48 0.000 1.058 -1.267 0 1
#> Item_49 0.000 0.969 -0.486 0 1
#> Item_50 0.000 1.086 -0.442 0 1
#>
#> $means
#> F1 F2
#> 0 0
#>
#> $cov
#> F1 F2
#> F1 1.000 0.409
#> F2 0.409 1.000
#>
#>
#> $Group_2
#> $items
#> a1 a2 d g u
#> Item_1 0.942 0.000 -1.195 0 1
#> Item_2 0.973 0.000 0.294 0 1
#> Item_3 0.833 0.000 1.131 0 1
#> Item_4 1.049 0.000 -2.575 0 1
#> Item_5 1.078 0.000 0.517 0 1
#> Item_6 0.903 0.000 0.610 0 1
#> Item_7 1.006 0.000 -0.476 0 1
#> Item_8 0.889 0.000 -0.501 0 1
#> Item_9 0.855 0.000 -0.604 0 1
#> Item_10 0.892 0.000 0.069 0 1
#> Item_11 0.931 0.000 0.498 0 1
#> Item_12 0.962 0.000 0.065 0 1
#> Item_13 0.845 0.000 0.311 0 1
#> Item_14 0.893 0.000 1.036 0 1
#> Item_15 0.998 0.000 1.919 0 1
#> Item_16 0.949 0.000 -0.155 0 1
#> Item_17 0.989 0.000 -0.545 0 1
#> Item_18 0.866 0.000 -0.945 0 1
#> Item_19 0.893 0.000 -0.872 0 1
#> Item_20 0.732 0.000 2.195 0 1
#> Item_21 0.854 0.000 0.059 0 1
#> Item_22 0.783 0.000 -0.498 0 1
#> Item_23 0.966 0.000 -0.561 0 1
#> Item_24 0.944 0.000 0.384 0 1
#> Item_25 0.940 0.000 -0.794 0 1
#> Item_26 0.000 0.979 -1.450 0 1
#> Item_27 0.000 0.999 0.603 0 1
#> Item_28 0.000 1.105 -1.108 0 1
#> Item_29 0.000 1.034 0.043 0 1
#> Item_30 0.000 0.974 -0.925 0 1
#> Item_31 0.000 0.998 1.989 0 1
#> Item_32 0.000 1.190 0.252 0 1
#> Item_33 0.000 1.064 0.076 0 1
#> Item_34 0.000 0.885 0.444 0 1
#> Item_35 0.000 1.065 -0.597 0 1
#> Item_36 0.000 1.080 -1.273 0 1
#> Item_37 0.000 1.034 -2.217 0 1
#> Item_38 0.000 1.040 -1.451 0 1
#> Item_39 0.000 1.160 -0.496 0 1
#> Item_40 0.000 1.015 -0.711 0 1
#> Item_41 0.000 0.946 1.416 0 1
#> Item_42 0.000 1.006 -1.144 0 1
#> Item_43 0.000 0.969 -0.818 0 1
#> Item_44 0.000 1.099 -0.322 0 1
#> Item_45 0.000 1.062 -1.103 0 1
#> Item_46 0.000 1.064 -0.951 0 1
#> Item_47 0.000 1.025 -1.122 0 1
#> Item_48 0.000 0.975 -1.194 0 1
#> Item_49 0.000 1.083 -0.461 0 1
#> Item_50 0.000 0.935 -0.512 0 1
#>
#> $means
#> F1 F2
#> 0.003 0.578
#>
#> $cov
#> F1 F2
#> F1 1.165 0.459
#> F2 0.459 1.340
#>
#>
plot(mod, degrees = c(45,45))
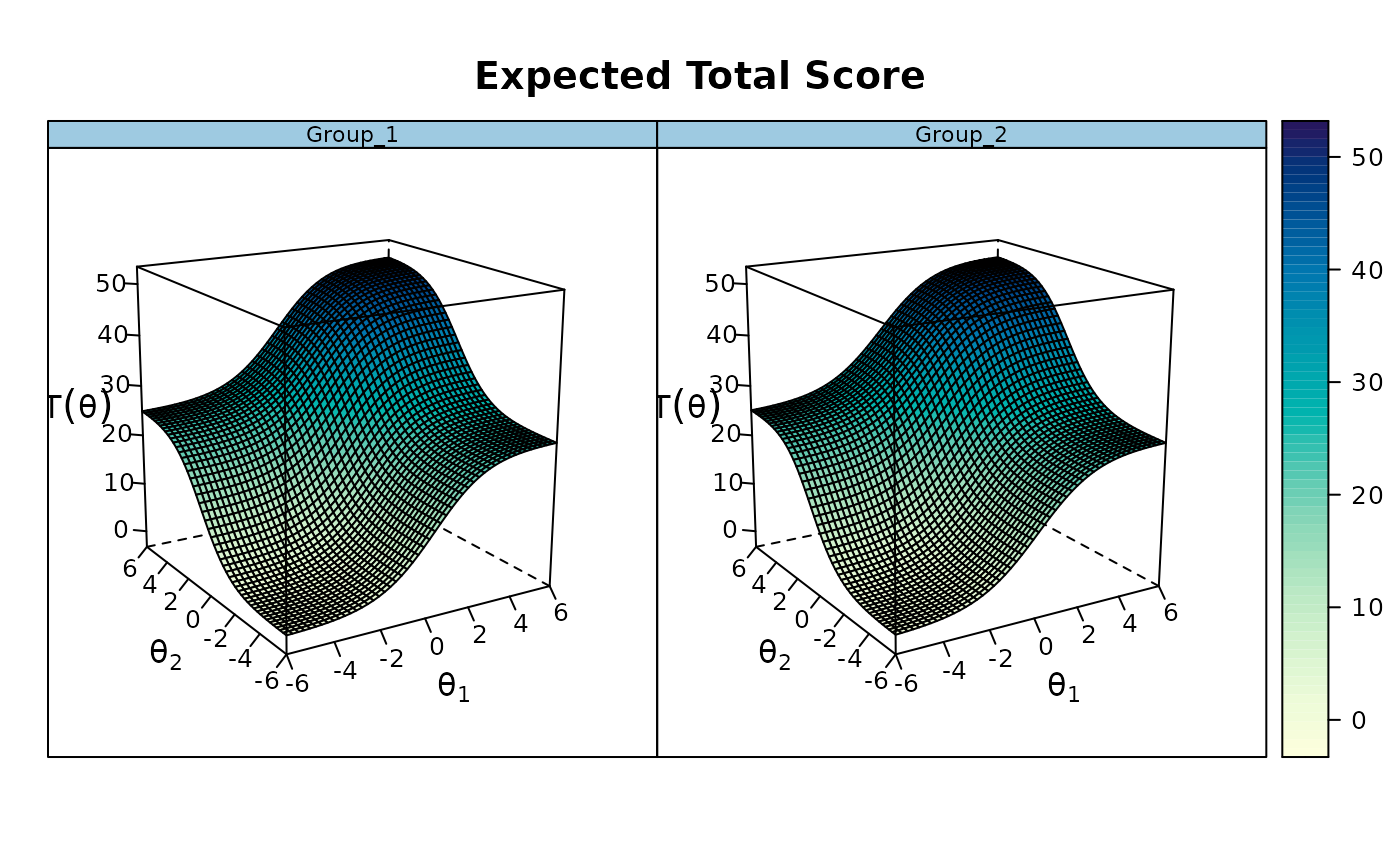 DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 50 1.803 1.803 1.831
DRF(mod, draws = 500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 50 1.803 1.232 2.303 44.608 1 0
#> uDRF Group_1,Group_2 50 1.803 1.232 2.303 47.432 2 0
#> dDRF Group_1,Group_2 50 1.831 1.278 2.354
# }
DRF(mod)
#> groups n_focal_items sDRF uDRF dDRF
#> 1 Group_1,Group_2 50 1.803 1.803 1.831
DRF(mod, draws = 500)
#> groups n_focal_items stat CI_2.5 CI_97.5 X2 df p
#> sDRF Group_1,Group_2 50 1.803 1.232 2.303 44.608 1 0
#> uDRF Group_1,Group_2 50 1.803 1.232 2.303 47.432 2 0
#> dDRF Group_1,Group_2 50 1.831 1.278 2.354
# }