mdirt fits a variety of item response models with discrete latent variables.
These include, but are not limited to, latent class analysis, multidimensional latent
class models, multidimensional discrete latent class models, DINA/DINO models,
grade of measurement models, C-RUM, and so on. If response models are not defined explicitly
then customized models can defined using the createItem function.
Usage
mdirt(
data,
model,
customTheta = NULL,
structure = NULL,
item.Q = NULL,
nruns = 1,
method = "EM",
covdata = NULL,
formula = NULL,
itemtype = "lca",
optimizer = "nlminb",
return_max = TRUE,
group = NULL,
GenRandomPars = FALSE,
verbose = TRUE,
pars = NULL,
technical = list(),
...
)Arguments
- data
a
matrixordata.framethat consists of numerically ordered data, organized in the form of integers, with missing data coded asNA- model
number of mutually exclusive classes to fit, or alternatively a more specific
mirt.modeldefinition (which reflects the so-called Q-matrix). Note that when using amirt.model, the order with which the syntax factors/attributes are defined are associated with the columns in thecustomThetainput- customTheta
input passed to
technical = list(customTheta = ...), but is included directly in this function for convenience. This input is most interesting for discrete latent models because it allows customized patterns of latent classes (i.e., defines the possible combinations of the latent attribute profile). The default builds the patterncustomTheta = diag(model), which is the typical pattern for the traditional latent class analysis whereby class membership mutually distinct and exhaustive. SeethetaCombfor a quick method to generate a matrix with all possible combinations- structure
an R formula allowing the profile probability patterns (i.e., the structural component of the model) to be fitted according to a log-linear model. When
NULL, all profile probabilities (except one) will be estimated. Use of this input requires that thecustomThetainput is supplied, and that the column names in this matrix match the names found within this formula- item.Q
a list of item-level Q-matrices indicating how the respective categories should be modeled by the underlying attributes. Each matrix must represent a \(K_i \times A\) matrix, where \(K_i\) represents the number of categories for the ith item, and \(A\) is the number of attributes included in the
Thetamatrix; otherwise, a value ofNULLwill default to a matrix consisting of 1's for each \(K_i \times A\) element except for the first row, which contains only 0's for proper identification. Incidentally, the first row of each matrixmustcontain only 0's so that the first category represents the reference category for identification- nruns
a numeric value indicating how many times the model should be fit to the data when using random starting values. If greater than 1,
GenRandomParsis set to true by default- method
estimation method. Can be 'EM' or 'BL' (see
mirtfor more details)- covdata
a data.frame of data used for latent regression models
- formula
an R formula (or list of formulas) indicating how the latent traits can be regressed using external covariates in
covdata. If a named list of formulas is supplied (where the names correspond to the latent trait/attribute names inmodel) then specific regression effects can be estimated for each factor. Supplying a single formula will estimate the regression parameters for all latent variables by default- itemtype
a vector indicating the itemtype associated with each item. For discrete models this is limited to only 'lca' or items defined using a
createItemdefinition- optimizer
optimizer used for the M-step, set to
'nlminb'by default. Seemirtfor more details- return_max
logical; when
nruns > 1, return the model that has the most optimal maximum likelihood criteria? If FALSE, returns a list of all the estimated objects- group
a factor variable indicating group membership used for multiple group analyses
- GenRandomPars
logical; use random starting values
- verbose
logical; turn on messages to the R console
- pars
used for modifying starting values; see
mirtfor details- technical
list of lower-level inputs. See
mirtfor details- ...
additional arguments to be passed to the estimation engine. See
mirtfor more details and examples
Details
Posterior classification accuracy for each response pattern may be obtained
via the fscores function. The summary() function will display
the category probability values given the class membership, which can also
be displayed graphically with plot(), while coef()
displays the raw coefficient values (and their standard errors, if estimated). Finally,
anova() is used to compare nested models, while
M2 and itemfit may be used for model fitting purposes.
'lca' model definition
The latent class IRT model with two latent classes has the form
$$P(x = k|\theta_1, \theta_2, a1, a2) = \frac{exp(a1 \theta_1 + a2 \theta_2)}{ \sum_j^K exp(a1 \theta_1 + a2 \theta_2)}$$
where the \(\theta\) values generally take on discrete points (such as 0 or 1). For proper identification, the first category slope parameters (\(a1\) and \(a2\)) are never freely estimated. Alternatively, supplying a different grid of \(\theta\) values will allow the estimation of similar models (multidimensional discrete models, grade of membership, etc.). See the examples below.
When the item.Q for is utilized, the above equation can be understood as
$$P(x = k|\theta_1, \theta_2, a1, a2) = \frac{exp(a1 \theta_1 Q_{j1} + a2 \theta_2 Q_{j2})}{ \sum_j^K exp(a1 \theta_1 Q_{j1} + a2 \theta_2 Q_{j2})}$$
where by construction Q is a \(K_i \times A\) matrix indicating whether the category should
be modeled according to the latent class structure. For the standard latent class model, the Q-matrix
has as many rows as categories, as many columns as the number of classes/attributes modeled,
and consist of 0's in the first row and 1's elsewhere. This of course can be over-written by passing
an alternative item.Q definition for each respective item.
References
Chalmers, R., P. (2012). mirt: A Multidimensional Item Response Theory Package for the R Environment. Journal of Statistical Software, 48(6), 1-29.
Proctor, C. H. (1970). A probabilistic formulation and statistical analysis for Guttman scaling. Psychometrika, 35, 73-78. doi:10.18637/jss.v048.i06
Author
Phil Chalmers rphilip.chalmers@gmail.com
Examples
# LSAT6 dataset
dat <- expand.table(LSAT6)
# fit with 2-3 latent classes
(mod2 <- mdirt(dat, 2))
#>
#> Call:
#> mdirt(data = dat, model = 2)
#>
#> Latent class model with 2 classes and 2 profiles.
#> Converged within 1e-04 tolerance after 363 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Latent density type: discrete
#>
#> Log-likelihood = -2467.408
#> Estimated parameters: 11
#> AIC = 4956.816
#> BIC = 5010.802; SABIC = 4975.865
#> G2 (20) = 22.74, p = 0.3018, RMSEA = 0.012
# \donttest{
(mod3 <- mdirt(dat, 3))
#> Warning: EM cycles terminated after 500 iterations.
#>
#> Call:
#> mdirt(data = dat, model = 3)
#>
#> Latent class model with 3 classes and 3 profiles.
#> FAILED TO CONVERGE within 1e-04 tolerance after 500 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Latent density type: discrete
#>
#> Log-likelihood = -2465.25
#> Estimated parameters: 17
#> AIC = 4964.5
#> BIC = 5047.932; SABIC = 4993.939
#> G2 (14) = 18.42, p = 0.1882, RMSEA = 0.018
summary(mod2)
#> $Item_1
#> category_1 category_2
#> P[1 0] 0.156 0.844
#> P[0 1] 0.037 0.963
#>
#> $Item_2
#> category_1 category_2
#> P[1 0] 0.485 0.515
#> P[0 1] 0.196 0.804
#>
#> $Item_3
#> category_1 category_2
#> P[1 0] 0.713 0.287
#> P[0 1] 0.317 0.683
#>
#> $Item_4
#> category_1 category_2
#> P[1 0] 0.401 0.599
#> P[0 1] 0.157 0.843
#>
#> $Item_5
#> category_1 category_2
#> P[1 0] 0.232 0.768
#> P[0 1] 0.080 0.920
#>
#> $Class.Probability
#> F1 F2 prob
#> Profile_1 1 0 0.329
#> Profile_2 0 1 0.671
#>
residuals(mod2)
#> Item_1 Item_2 Item_3 Item_4 Item_5
#> Item_1 NA 0.010 0.020 -0.011 -0.018
#> Item_2 0.109 NA 0.003 -0.018 0.022
#> Item_3 0.412 0.009 NA 0.008 -0.026
#> Item_4 0.132 0.313 0.060 NA 0.040
#> Item_5 0.331 0.487 0.680 1.566 NA
residuals(mod2, type = 'exp')
#> Item_1 Item_2 Item_3 Item_4 Item_5 freq exp std.res
#> 1 0 0 0 0 0 3 1.662 1.038
#> 2 0 0 0 0 1 6 5.673 0.137
#> 3 0 0 0 1 0 2 2.556 -0.348
#> 4 0 0 0 1 1 11 9.333 0.546
#> 5 0 0 1 0 0 1 0.702 0.356
#> 6 0 0 1 0 1 1 2.670 -1.022
#> 7 0 0 1 1 0 3 1.211 1.626
#> 8 0 0 1 1 1 4 5.855 -0.767
#> 9 0 1 0 0 0 1 1.826 -0.611
#> 10 0 1 0 0 1 8 6.708 0.499
#> 11 0 1 0 1 1 16 13.561 0.662
#> 12 0 1 1 0 1 3 4.297 -0.625
#> 13 0 1 1 1 0 2 1.972 0.020
#> 14 0 1 1 1 1 15 14.075 0.247
#> 15 1 0 0 0 0 10 9.422 0.188
#> 16 1 0 0 0 1 29 35.372 -1.071
#> 17 1 0 0 1 0 14 16.027 -0.506
#> 18 1 0 0 1 1 81 75.302 0.657
#> 19 1 0 1 0 0 3 4.672 -0.773
#> 20 1 0 1 0 1 28 24.369 0.736
#> 21 1 0 1 1 0 15 11.213 1.131
#> 22 1 0 1 1 1 80 84.968 -0.539
#> 23 1 1 0 0 0 16 11.551 1.309
#> 24 1 1 0 0 1 56 55.154 0.114
#> 25 1 1 0 1 0 21 25.287 -0.853
#> 26 1 1 0 1 1 173 174.541 -0.117
#> 27 1 1 1 0 0 11 8.273 0.948
#> 28 1 1 1 0 1 61 63.783 -0.348
#> 29 1 1 1 1 0 28 29.723 -0.316
#> 30 1 1 1 1 1 298 294.334 0.214
anova(mod2, mod3)
#> AIC SABIC HQ BIC logLik X2 df p
#> mod2 4956.816 4975.865 4977.335 5010.802 -2467.408
#> mod3 4964.500 4993.939 4996.210 5047.932 -2465.250 4.317 6 0.634
M2(mod2)
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR TLI
#> stats 4.603509 4 0.3304498 0.01228935 0 0.05069941 0.02122285 0.973442
#> CFI
#> stats 0.9893768
itemfit(mod2)
#> item S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
#> 1 Item_1 0.433 2 0 0.805
#> 2 Item_2 1.702 2 0 0.427
#> 3 Item_3 0.747 1 0 0.387
#> 4 Item_4 0.184 2 0 0.912
#> 5 Item_5 0.145 2 0 0.930
# generate classification plots
plot(mod2)
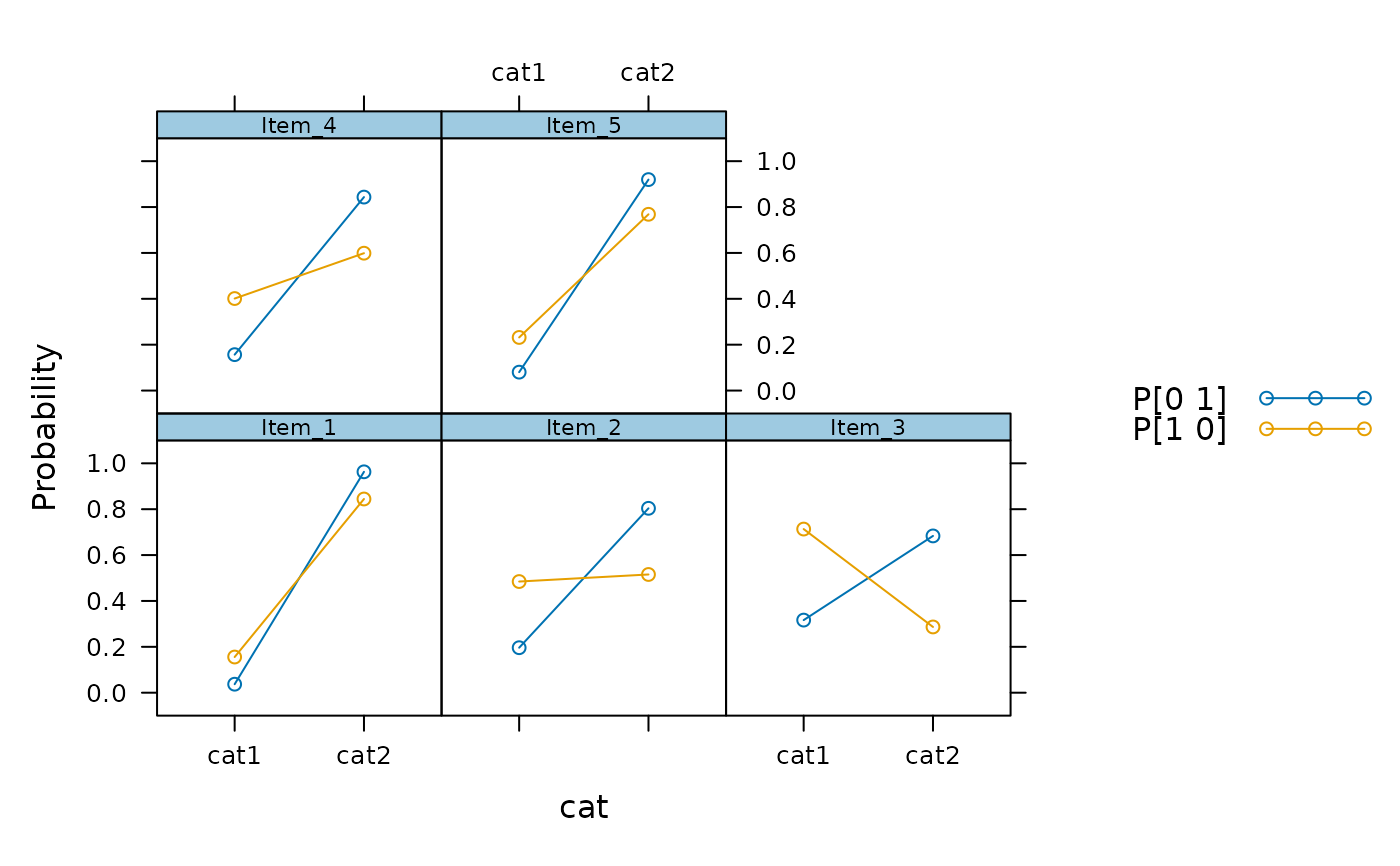plot(mod2, facet_items = FALSE)
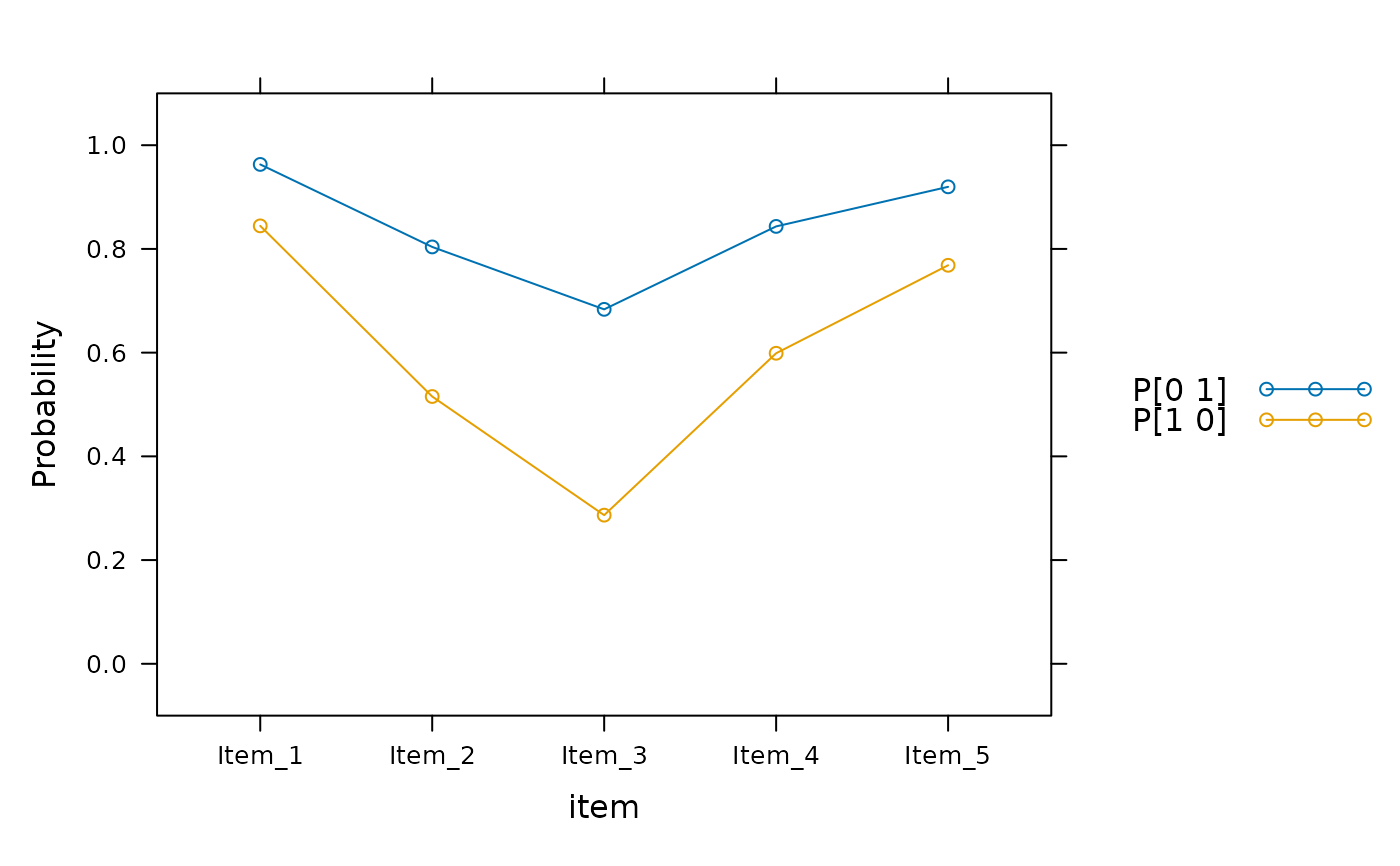
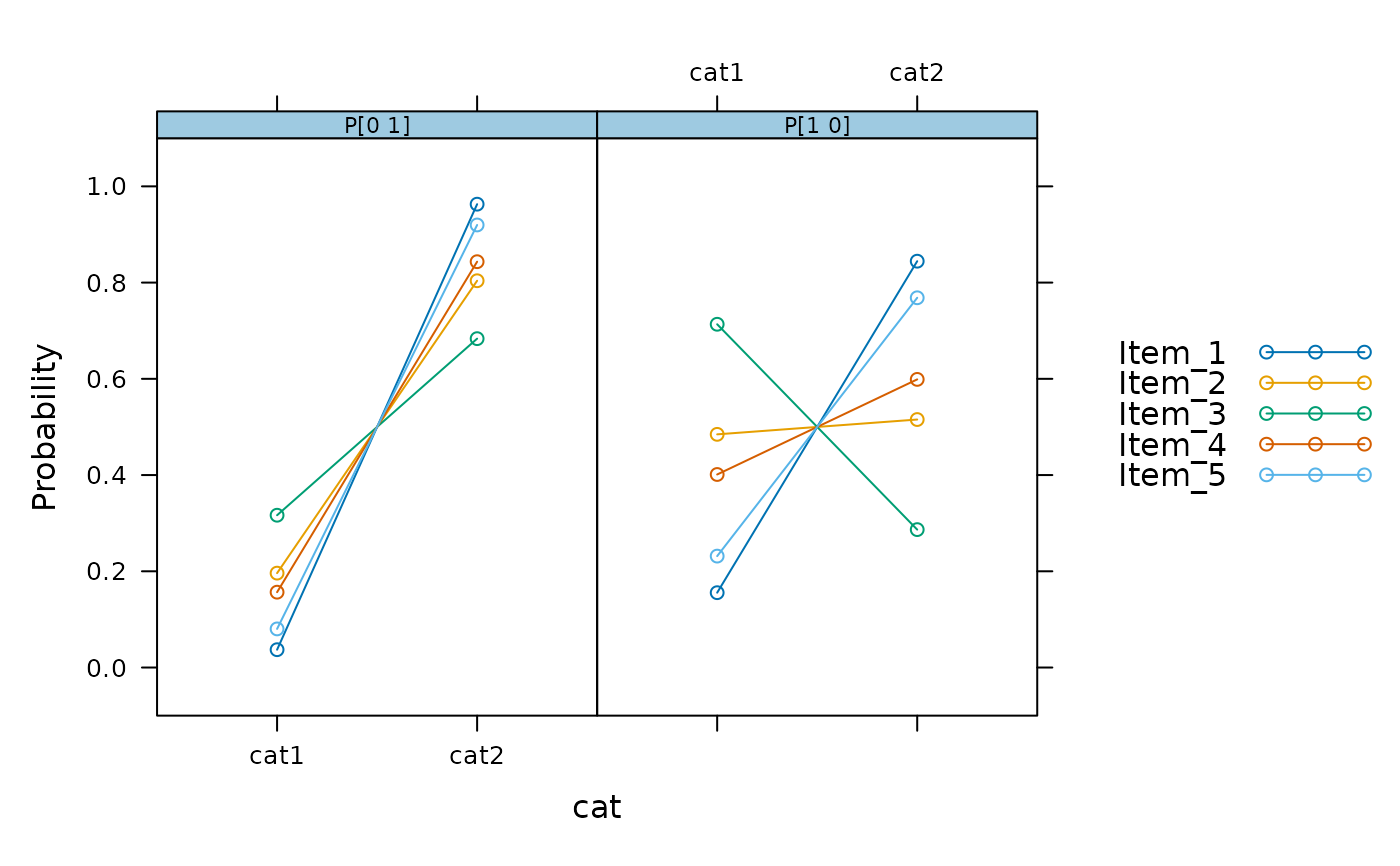plot(mod2, profile = TRUE)
# available for polytomous data
mod <- mdirt(Science, 2)
summary(mod)
#> $Comfort
#> category_1 category_2 category_3 category_4
#> P[1 0] 0.018 0.095 0.766 0.121
#> P[0 1] 0.000 0.051 0.474 0.475
#>
#> $Work
#> category_1 category_2 category_3 category_4
#> P[1 0] 0.115 0.329 0.520 0.036
#> P[0 1] 0.013 0.065 0.537 0.385
#>
#> $Future
#> category_1 category_2 category_3 category_4
#> P[1 0] 0.051 0.262 0.619 0.068
#> P[0 1] 0.001 0.000 0.340 0.659
#>
#> $Benefit
#> category_1 category_2 category_3 category_4
#> P[1 0] 0.072 0.323 0.516 0.089
#> P[0 1] 0.011 0.097 0.437 0.455
#>
#> $Class.Probability
#> F1 F2 prob
#> Profile_1 1 0 0.701
#> Profile_2 0 1 0.299
#>
plot(mod)
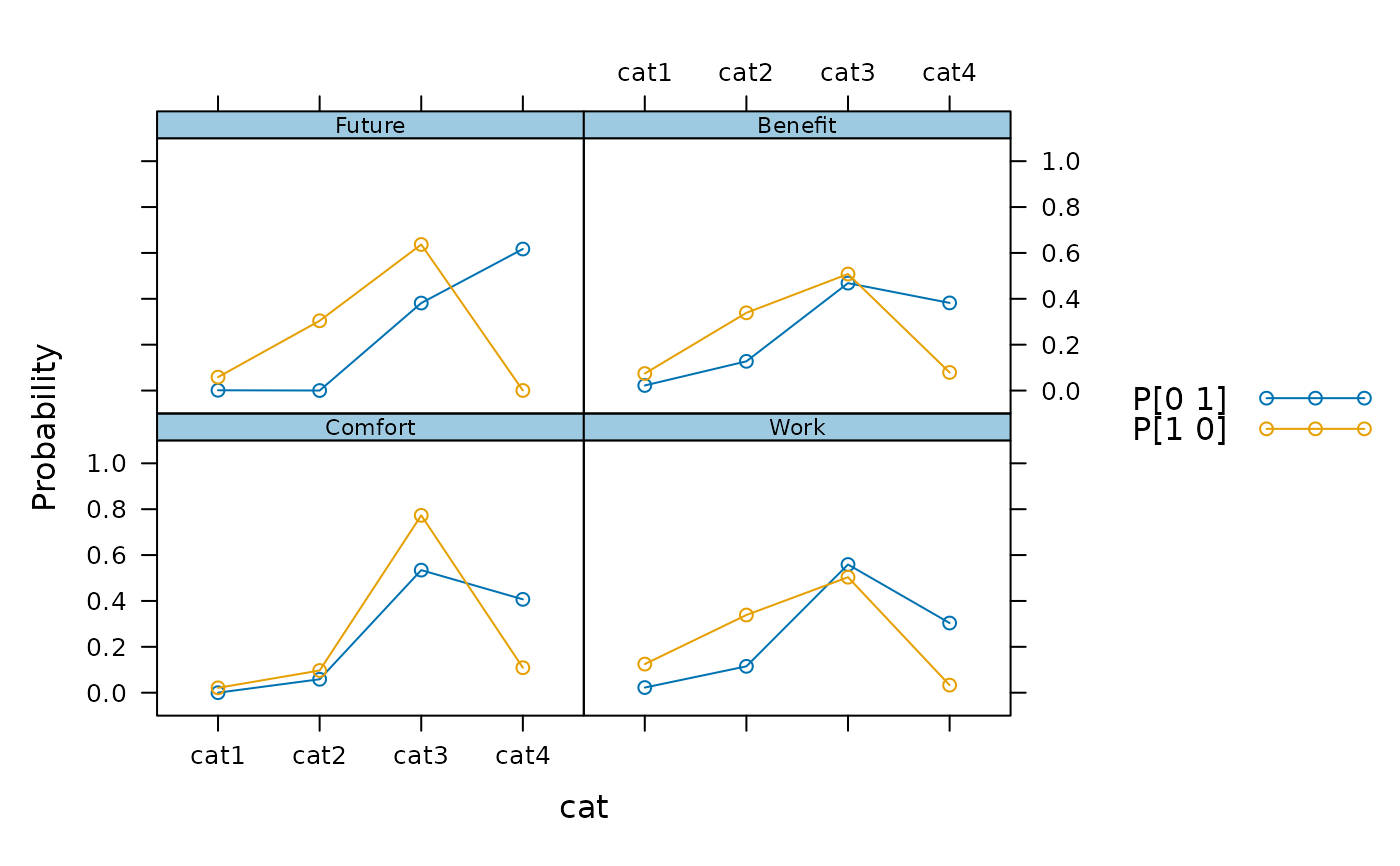plot(mod, profile=TRUE)
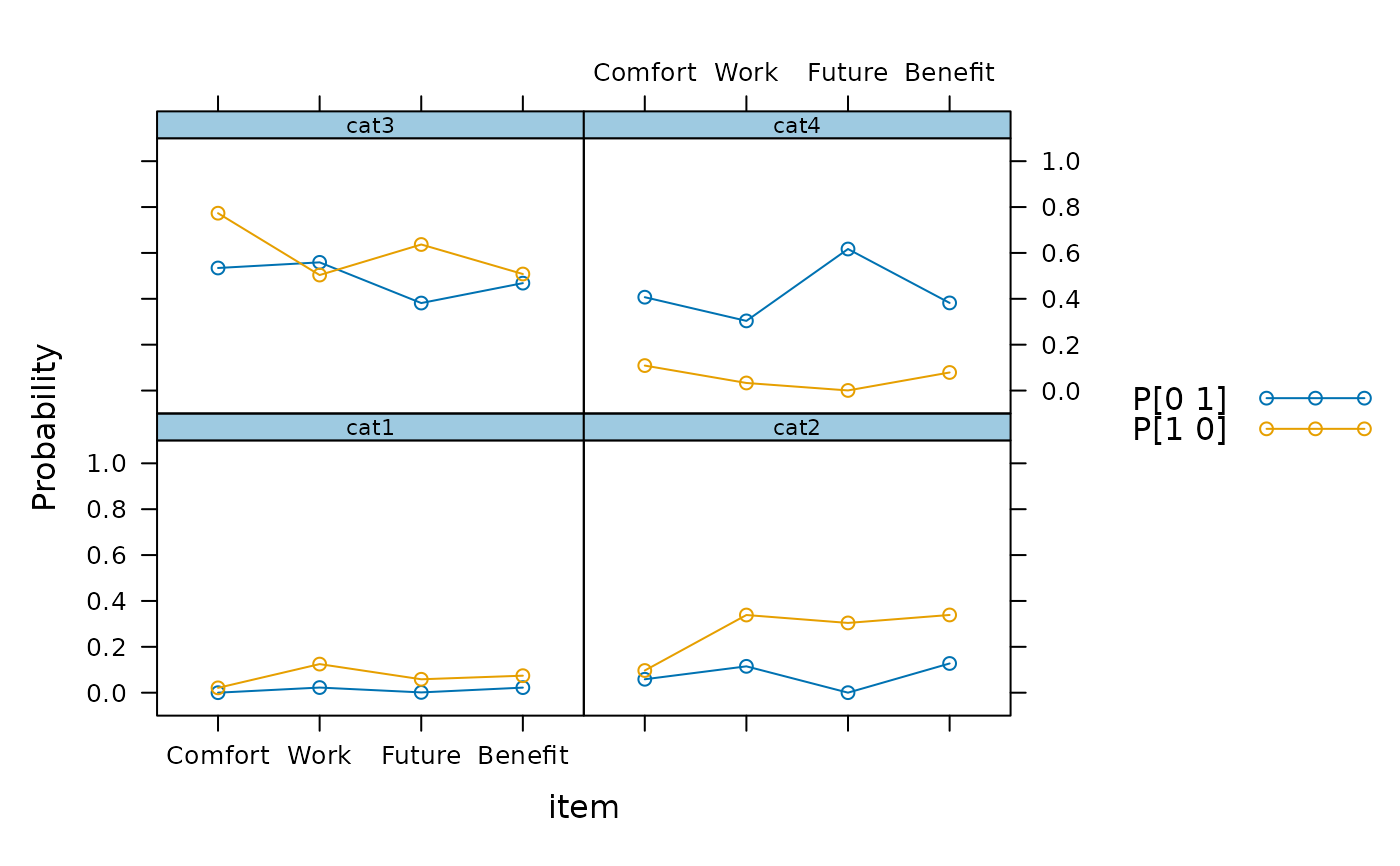# classification based on response patterns
fscores(mod2, full.scores = FALSE)
#> Item_1 Item_2 Item_3 Item_4 Item_5 Class_1 Class_2
#> [1,] 0 0 0 0 0 0.98832539 0.01167461
#> [2,] 0 0 0 0 1 0.96080421 0.03919579
#> [3,] 0 0 0 1 0 0.95911420 0.04088580
#> [4,] 0 0 0 1 1 0.87167305 0.12832695
#> [5,] 0 0 1 0 0 0.94030147 0.05969853
#> [6,] 0 0 1 0 1 0.82016986 0.17983014
#> [7,] 0 0 1 1 0 0.81359256 0.18640744
#> [8,] 0 0 1 1 1 0.55826672 0.44173328
#> [9,] 0 1 0 0 0 0.95646627 0.04353373
#> [10,] 0 1 0 0 1 0.86416411 0.13583589
#> [11,] 0 1 0 1 1 0.63805843 0.36194157
#> [12,] 0 1 1 0 1 0.54205358 0.45794642
#> [13,] 0 1 1 1 0 0.53111944 0.46888056
#> [14,] 0 1 1 1 1 0.24698538 0.75301462
#> [15,] 1 0 0 0 0 0.94648118 0.05351882
#> [16,] 1 0 0 0 1 0.83662440 0.16337560
#> [17,] 1 0 0 1 0 0.83052457 0.16947543
#> [18,] 1 0 0 1 1 0.58660671 0.41339329
#> [19,] 1 0 1 0 0 0.76692257 0.23307743
#> [20,] 1 0 1 0 1 0.48790756 0.51209244
#> [21,] 1 0 1 1 0 0.47692814 0.52307186
#> [22,] 1 0 1 1 1 0.20887048 0.79112952
#> [23,] 1 1 0 0 0 0.82110202 0.17889798
#> [24,] 1 1 0 0 1 0.57063375 0.42936625
#> [25,] 1 1 0 1 0 0.55982786 0.44017214
#> [26,] 1 1 0 1 1 0.26915168 0.73084832
#> [27,] 1 1 1 0 0 0.46061404 0.53938596
#> [28,] 1 1 1 0 1 0.19825043 0.80174957
#> [29,] 1 1 1 1 0 0.19135355 0.80864645
#> [30,] 1 1 1 1 1 0.06412585 0.93587415
# classify individuals either with the largest posterior probability.....
fs <- fscores(mod2)
head(fs)
#> Class_1 Class_2
#> 1 0.9883254 0.01167461
#> 2 0.9883254 0.01167461
#> 3 0.9883254 0.01167461
#> 4 0.9608042 0.03919579
#> 5 0.9608042 0.03919579
#> 6 0.9608042 0.03919579
classes <- 1:2
class_max <- classes[apply(apply(fs, 1, max) == fs, 1, which)]
table(class_max)
#> class_max
#> 1 2
#> 291 709
# ... or by probability sampling (i.e., plausible value draws)
class_prob <- apply(fs, 1, function(x) sample(1:2, 1, prob=x))
table(class_prob)
#> class_prob
#> 1 2
#> 325 675
# plausible value imputations for stochastic classification in both classes
pvs <- fscores(mod2, plausible.draws=10)
tabs <- lapply(pvs, function(x) apply(x, 2, table))
tabs[[1]]
#> [,1] [,2]
#> 0 678 306
#> 1 322 694
# fit with random starting points (run in parallel to save time)
if(interactive()) mirtCluster()
mod <- mdirt(dat, 2, nruns=10)
#> Model log-likelihoods:
#> [1] -2467.408 -2467.408 -2467.408 -2467.408 -2467.408 -2467.408 -2467.408
#> [8] -2467.408 -2467.408 -2467.408
#--------------------------
# Grade of measurement model
# define a custom Theta grid for including a 'fuzzy' class membership
(Theta <- matrix(c(1, 0, .5, .5, 0, 1), nrow=3 , ncol=2, byrow=TRUE))
#> [,1] [,2]
#> [1,] 1.0 0.0
#> [2,] 0.5 0.5
#> [3,] 0.0 1.0
(mod_gom <- mdirt(dat, 2, customTheta = Theta))
#> Warning: EM cycles terminated after 500 iterations.
#>
#> Call:
#> mdirt(data = dat, model = 2, customTheta = Theta)
#>
#> Latent class model with 2 classes and 3 profiles.
#> FAILED TO CONVERGE within 1e-04 tolerance after 500 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Latent density type: discrete
#>
#> Log-likelihood = -2466.602
#> Estimated parameters: 12
#> AIC = 4957.205
#> BIC = 5016.098; SABIC = 4977.985
#> G2 (19) = 21.13, p = 0.3298, RMSEA = 0.011
summary(mod_gom)
#> $Item_1
#> category_1 category_2
#> P[1 0] 0.322 0.678
#> P[0.5 0.5] 0.102 0.898
#> P[0 1] 0.026 0.974
#>
#> $Item_2
#> category_1 category_2
#> P[1 0] 0.692 0.308
#> P[0.5 0.5] 0.386 0.614
#> P[0 1] 0.150 0.850
#>
#> $Item_3
#> category_1 category_2
#> P[1 0] 0.866 0.134
#> P[0.5 0.5] 0.592 0.408
#> P[0 1] 0.247 0.753
#>
#> $Item_4
#> category_1 category_2
#> P[1 0] 0.603 0.397
#> P[0.5 0.5] 0.313 0.687
#> P[0 1] 0.120 0.880
#>
#> $Item_5
#> category_1 category_2
#> P[1 0] 0.398 0.602
#> P[0.5 0.5] 0.171 0.829
#> P[0 1] 0.061 0.939
#>
#> $Class.Probability
#> F1 F2 prob
#> Profile_1 1.0 0.0 0.037
#> Profile_2 0.5 0.5 0.513
#> Profile_3 0.0 1.0 0.450
#>
#-----------------
# Multidimensional discrete latent class model
dat <- key2binary(SAT12,
key = c(1,4,5,2,3,1,2,1,3,1,2,4,2,1,5,3,4,4,1,4,3,3,4,1,3,5,1,3,1,5,4,5))
# define Theta grid for three latent classes
(Theta <- thetaComb(0:1, 3))
#> [,1] [,2] [,3]
#> [1,] 0 0 0
#> [2,] 1 0 0
#> [3,] 0 1 0
#> [4,] 1 1 0
#> [5,] 0 0 1
#> [6,] 1 0 1
#> [7,] 0 1 1
#> [8,] 1 1 1
(mod_discrete <- mdirt(dat, 3, customTheta = Theta))
#>
#> Call:
#> mdirt(data = dat, model = 3, customTheta = Theta)
#>
#> Latent class model with 3 classes and 8 profiles.
#> Converged within 1e-04 tolerance after 139 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Latent density type: discrete
#>
#> Log-likelihood = -9429.721
#> Estimated parameters: 103
#> AIC = 19065.44
#> BIC = 19518.33; SABIC = 19191.33
#> G2 (4294967192) = 11189.72, p = 1, RMSEA = 0
summary(mod_discrete)
#> $Item.1
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.868 0.132
#> P[0 1 0] 0.460 0.540
#> P[1 1 0] 0.849 0.151
#> P[0 0 1] 0.341 0.659
#> P[1 0 1] 0.773 0.227
#> P[0 1 1] 0.306 0.694
#> P[1 1 1] 0.744 0.256
#>
#> $Item.2
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.945 0.055
#> P[0 1 0] 0.165 0.835
#> P[1 1 0] 0.774 0.226
#> P[0 0 1] 0.073 0.927
#> P[1 0 1] 0.575 0.425
#> P[0 1 1] 0.015 0.985
#> P[1 1 1] 0.211 0.789
#>
#> $Item.3
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.929 0.071
#> P[0 1 0] 0.337 0.663
#> P[1 1 0] 0.870 0.130
#> P[0 0 1] 0.271 0.729
#> P[1 0 1] 0.830 0.170
#> P[0 1 1] 0.159 0.841
#> P[1 1 1] 0.712 0.288
#>
#> $Item.4
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.844 0.156
#> P[0 1 0] 0.223 0.777
#> P[1 1 0] 0.609 0.391
#> P[0 0 1] 0.428 0.572
#> P[1 0 1] 0.802 0.198
#> P[0 1 1] 0.177 0.823
#> P[1 1 1] 0.538 0.462
#>
#> $Item.5
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.837 0.163
#> P[0 1 0] 0.263 0.737
#> P[1 1 0] 0.647 0.353
#> P[0 0 1] 0.137 0.863
#> P[1 0 1] 0.449 0.551
#> P[0 1 1] 0.053 0.947
#> P[1 1 1] 0.225 0.775
#>
#> $Item.6
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.943 0.057
#> P[0 1 0] 0.334 0.666
#> P[1 1 0] 0.893 0.107
#> P[0 0 1] 0.473 0.527
#> P[1 0 1] 0.937 0.063
#> P[0 1 1] 0.311 0.689
#> P[1 1 1] 0.882 0.118
#>
#> $Item.7
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.766 0.234
#> P[0 1 0] 0.283 0.717
#> P[1 1 0] 0.564 0.436
#> P[0 0 1] 0.088 0.912
#> P[1 0 1] 0.240 0.760
#> P[0 1 1] 0.037 0.963
#> P[1 1 1] 0.111 0.889
#>
#> $Item.8
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.866 0.134
#> P[0 1 0] 0.573 0.427
#> P[1 1 0] 0.897 0.103
#> P[0 0 1] 0.422 0.578
#> P[1 0 1] 0.825 0.175
#> P[0 1 1] 0.495 0.505
#> P[1 1 1] 0.864 0.136
#>
#> $Item.9
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.457 0.543
#> P[0 1 0] 0.253 0.747
#> P[1 1 0] 0.221 0.779
#> P[0 0 1] 0.145 0.855
#> P[1 0 1] 0.124 0.876
#> P[0 1 1] 0.054 0.946
#> P[1 1 1] 0.046 0.954
#>
#> $Item.10
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.904 0.096
#> P[0 1 0] 0.298 0.702
#> P[1 1 0] 0.800 0.200
#> P[0 0 1] 0.189 0.811
#> P[1 0 1] 0.686 0.314
#> P[0 1 1] 0.090 0.910
#> P[1 1 1] 0.482 0.518
#>
#> $Item.11
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.987 0.013
#> P[0 1 0] 0.001 0.999
#> P[1 1 0] 0.039 0.961
#> P[0 0 1] 0.000 1.000
#> P[1 0 1] 0.014 0.986
#> P[0 1 1] 0.000 1.000
#> P[1 1 1] 0.000 1.000
#>
#> $Item.12
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.621 0.379
#> P[0 1 0] 0.434 0.566
#> P[1 1 0] 0.557 0.443
#> P[0 0 1] 0.523 0.477
#> P[1 0 1] 0.643 0.357
#> P[0 1 1] 0.457 0.543
#> P[1 1 1] 0.580 0.420
#>
#> $Item.13
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.849 0.151
#> P[0 1 0] 0.316 0.684
#> P[1 1 0] 0.722 0.278
#> P[0 0 1] 0.087 0.913
#> P[1 0 1] 0.348 0.652
#> P[0 1 1] 0.042 0.958
#> P[1 1 1] 0.198 0.802
#>
#> $Item.14
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.857 0.143
#> P[0 1 0] 0.108 0.892
#> P[1 1 0] 0.421 0.579
#> P[0 0 1] 0.113 0.887
#> P[1 0 1] 0.432 0.568
#> P[0 1 1] 0.015 0.985
#> P[1 1 1] 0.085 0.915
#>
#> $Item.15
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.742 0.258
#> P[0 1 0] 0.289 0.711
#> P[1 1 0] 0.539 0.461
#> P[0 0 1] 0.054 0.946
#> P[1 0 1] 0.141 0.859
#> P[0 1 1] 0.023 0.977
#> P[1 1 1] 0.062 0.938
#>
#> $Item.16
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.846 0.154
#> P[0 1 0] 0.298 0.702
#> P[1 1 0] 0.700 0.300
#> P[0 0 1] 0.315 0.685
#> P[1 0 1] 0.716 0.284
#> P[0 1 1] 0.164 0.836
#> P[1 1 1] 0.517 0.483
#>
#> $Item.17
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.694 0.306
#> P[0 1 0] 0.062 0.938
#> P[1 1 0] 0.130 0.870
#> P[0 0 1] 0.008 0.992
#> P[1 0 1] 0.018 0.982
#> P[0 1 1] 0.001 0.999
#> P[1 1 1] 0.001 0.999
#>
#> $Item.18
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.977 0.023
#> P[0 1 0] 0.217 0.783
#> P[1 1 0] 0.922 0.078
#> P[0 0 1] 0.090 0.910
#> P[1 0 1] 0.808 0.192
#> P[0 1 1] 0.027 0.973
#> P[1 1 1] 0.539 0.461
#>
#> $Item.19
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.830 0.170
#> P[0 1 0] 0.291 0.709
#> P[1 1 0] 0.668 0.332
#> P[0 0 1] 0.200 0.800
#> P[1 0 1] 0.550 0.450
#> P[0 1 1] 0.093 0.907
#> P[1 1 1] 0.334 0.666
#>
#> $Item.20
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.918 0.082
#> P[0 1 0] 0.038 0.962
#> P[1 1 0] 0.305 0.695
#> P[0 0 1] 0.017 0.983
#> P[1 0 1] 0.164 0.836
#> P[0 1 1] 0.001 0.999
#> P[1 1 1] 0.008 0.992
#>
#> $Item.21
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.434 0.566
#> P[0 1 0] 0.223 0.777
#> P[1 1 0] 0.180 0.820
#> P[0 0 1] 0.110 0.890
#> P[1 0 1] 0.086 0.914
#> P[0 1 1] 0.034 0.966
#> P[1 1 1] 0.026 0.974
#>
#> $Item.22
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.996 0.004
#> P[0 1 0] 0.001 0.999
#> P[1 1 0] 0.209 0.791
#> P[0 0 1] 0.000 1.000
#> P[1 0 1] 0.055 0.945
#> P[0 1 1] 0.000 1.000
#> P[1 1 1] 0.000 1.000
#>
#> $Item.23
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.865 0.135
#> P[0 1 0] 0.283 0.717
#> P[1 1 0] 0.716 0.284
#> P[0 0 1] 0.423 0.577
#> P[1 0 1] 0.824 0.176
#> P[0 1 1] 0.224 0.776
#> P[1 1 1] 0.649 0.351
#>
#> $Item.24
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.824 0.176
#> P[0 1 0] 0.301 0.699
#> P[1 1 0] 0.668 0.332
#> P[0 0 1] 0.068 0.932
#> P[1 0 1] 0.256 0.744
#> P[0 1 1] 0.031 0.969
#> P[1 1 1] 0.129 0.871
#>
#> $Item.25
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.869 0.131
#> P[0 1 0] 0.350 0.650
#> P[1 1 0] 0.782 0.218
#> P[0 0 1] 0.280 0.720
#> P[1 0 1] 0.721 0.279
#> P[0 1 1] 0.174 0.826
#> P[1 1 1] 0.583 0.417
#>
#> $Item.26
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.967 0.033
#> P[0 1 0] 0.140 0.860
#> P[1 1 0] 0.825 0.175
#> P[0 0 1] 0.093 0.907
#> P[1 0 1] 0.748 0.252
#> P[0 1 1] 0.016 0.984
#> P[1 1 1] 0.326 0.674
#>
#> $Item.27
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.838 0.162
#> P[0 1 0] 0.137 0.863
#> P[1 1 0] 0.451 0.549
#> P[0 0 1] 0.023 0.977
#> P[1 0 1] 0.110 0.890
#> P[0 1 1] 0.004 0.996
#> P[1 1 1] 0.019 0.981
#>
#> $Item.28
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.888 0.112
#> P[0 1 0] 0.222 0.778
#> P[1 1 0] 0.693 0.307
#> P[0 0 1] 0.163 0.837
#> P[1 0 1] 0.606 0.394
#> P[0 1 1] 0.053 0.947
#> P[1 1 1] 0.305 0.695
#>
#> $Item.29
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.893 0.107
#> P[0 1 0] 0.292 0.708
#> P[1 1 0] 0.774 0.226
#> P[0 0 1] 0.323 0.677
#> P[1 0 1] 0.799 0.201
#> P[0 1 1] 0.164 0.836
#> P[1 1 1] 0.620 0.380
#>
#> $Item.30
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.698 0.302
#> P[0 1 0] 0.455 0.545
#> P[1 1 0] 0.659 0.341
#> P[0 0 1] 0.378 0.622
#> P[1 0 1] 0.584 0.416
#> P[0 1 1] 0.336 0.664
#> P[1 1 1] 0.539 0.461
#>
#> $Item.31
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.977 0.023
#> P[0 1 0] 0.024 0.976
#> P[1 1 0] 0.509 0.491
#> P[0 0 1] 0.005 0.995
#> P[1 0 1] 0.166 0.834
#> P[0 1 1] 0.000 1.000
#> P[1 1 1] 0.005 0.995
#>
#> $Item.32
#> category_1 category_2
#> P[0 0 0] 0.500 0.500
#> P[1 0 0] 0.729 0.271
#> P[0 1 0] 0.567 0.433
#> P[1 1 0] 0.779 0.221
#> P[0 0 1] 0.702 0.298
#> P[1 0 1] 0.863 0.137
#> P[0 1 1] 0.755 0.245
#> P[1 1 1] 0.892 0.108
#>
#> $Class.Probability
#> F1 F2 F3 prob
#> Profile_1 0 0 0 0.000
#> Profile_2 1 0 0 0.004
#> Profile_3 0 1 0 0.002
#> Profile_4 1 1 0 0.194
#> Profile_5 0 0 1 0.084
#> Profile_6 1 0 1 0.368
#> Profile_7 0 1 1 0.058
#> Profile_8 1 1 1 0.290
#>
# Located latent class model
model <- mirt.model('C1 = 1-32
C2 = 1-32
C3 = 1-32
CONSTRAIN = (1-32, a1), (1-32, a2), (1-32, a3)')
(mod_located <- mdirt(dat, model, customTheta = diag(3)))
#>
#> Call:
#> mdirt(data = dat, model = model, customTheta = diag(3))
#>
#> Latent class model with 3 classes and 3 profiles.
#> Converged within 1e-04 tolerance after 373 EM iterations.
#> mirt version: 1.43
#> M-step optimizer: nlminb
#> EM acceleration: Ramsay
#> Latent density type: discrete
#>
#> Log-likelihood = -12771.08
#> Estimated parameters: 98
#> AIC = 25552.15
#> BIC = 25574.14; SABIC = 25558.26
#> G2 (4294967290) = 17872.43, p = 1, RMSEA = 0
summary(mod_located)
#> $Item.1
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.2
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.3
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.4
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.5
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.6
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.7
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.8
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.9
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.10
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.11
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.12
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.13
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.14
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.15
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.16
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.17
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.18
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.19
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.20
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.21
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.22
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.23
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.24
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.25
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.26
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.27
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.28
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.29
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.30
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.31
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Item.32
#> category_1 category_2
#> P[1 0 0] 0.578 0.422
#> P[0 1 0] 0.410 0.590
#> P[0 0 1] 0.190 0.810
#>
#> $Class.Probability
#> C1 C2 C3 prob
#> Profile_1 1 0 0 0.339
#> Profile_2 0 1 0 0.497
#> Profile_3 0 0 1 0.164
#>
#-----------------
### DINA model example
# generate some suitable data for a two dimensional DINA application
# (first columns are intercepts)
set.seed(1)
Theta <- expand.table(matrix(c(1,0,0,0,
1,1,0,0,
1,0,1,0,
1,1,1,1), 4, 4, byrow=TRUE),
freq = c(200,200,100,500))
a <- matrix(c(rnorm(15, -1.5, .5), rlnorm(5, .2, .3), numeric(15), rlnorm(5, .2, .3),
numeric(15), rlnorm(5, .2, .3)), 15, 4)
guess <- plogis(a[11:15,1]) # population guess
slip <- 1 - plogis(rowSums(a[11:15,])) # population slip
dat <- simdata(a, Theta=Theta, itemtype = 'lca')
# first column is the intercept, 2nd and 3rd are attributes
theta <- cbind(1, thetaComb(0:1, 2))
theta <- cbind(theta, theta[,2] * theta[,3]) #DINA interaction of main attributes
model <- mirt.model('Intercept = 1-15
A1 = 1-5
A2 = 6-10
A1A2 = 11-15')
# last 5 items are DINA (first 10 are unidimensional C-RUMs)
DINA <- mdirt(dat, model, customTheta = theta)
coef(DINA, simplify=TRUE)
#> $items
#> a1 a2 a3 a4
#> Item_1 -1.630 1.115 0.000 0.000
#> Item_2 -1.052 0.841 0.000 0.000
#> Item_3 -1.582 1.271 0.000 0.000
#> Item_4 -0.388 1.229 0.000 0.000
#> Item_5 -1.054 1.340 0.000 0.000
#> Item_6 -2.569 0.000 2.500 0.000
#> Item_7 -1.100 0.000 1.435 0.000
#> Item_8 -1.103 0.000 1.054 0.000
#> Item_9 -1.474 0.000 1.041 0.000
#> Item_10 -1.620 0.000 1.359 0.000
#> Item_11 -0.542 0.000 0.000 0.997
#> Item_12 -1.584 0.000 0.000 1.609
#> Item_13 -1.881 0.000 0.000 0.934
#> Item_14 -2.663 0.000 0.000 0.912
#> Item_15 -0.813 0.000 0.000 1.005
#>
#> $group.intercepts
#> c1 c2 c3
#> par -0.545 -1.53 -1.468
#>
summary(DINA)
#> $Item_1
#> category_1 category_2
#> P[1 0 0 0] 0.836 0.164
#> P[1 1 0 0] 0.626 0.374
#> P[1 0 1 0] 0.836 0.164
#> P[1 1 1 1] 0.626 0.374
#>
#> $Item_2
#> category_1 category_2
#> P[1 0 0 0] 0.741 0.259
#> P[1 1 0 0] 0.553 0.447
#> P[1 0 1 0] 0.741 0.259
#> P[1 1 1 1] 0.553 0.447
#>
#> $Item_3
#> category_1 category_2
#> P[1 0 0 0] 0.829 0.171
#> P[1 1 0 0] 0.577 0.423
#> P[1 0 1 0] 0.829 0.171
#> P[1 1 1 1] 0.577 0.423
#>
#> $Item_4
#> category_1 category_2
#> P[1 0 0 0] 0.596 0.404
#> P[1 1 0 0] 0.301 0.699
#> P[1 0 1 0] 0.596 0.404
#> P[1 1 1 1] 0.301 0.699
#>
#> $Item_5
#> category_1 category_2
#> P[1 0 0 0] 0.742 0.258
#> P[1 1 0 0] 0.429 0.571
#> P[1 0 1 0] 0.742 0.258
#> P[1 1 1 1] 0.429 0.571
#>
#> $Item_6
#> category_1 category_2
#> P[1 0 0 0] 0.929 0.071
#> P[1 1 0 0] 0.929 0.071
#> P[1 0 1 0] 0.517 0.483
#> P[1 1 1 1] 0.517 0.483
#>
#> $Item_7
#> category_1 category_2
#> P[1 0 0 0] 0.750 0.250
#> P[1 1 0 0] 0.750 0.250
#> P[1 0 1 0] 0.417 0.583
#> P[1 1 1 1] 0.417 0.583
#>
#> $Item_8
#> category_1 category_2
#> P[1 0 0 0] 0.751 0.249
#> P[1 1 0 0] 0.751 0.249
#> P[1 0 1 0] 0.512 0.488
#> P[1 1 1 1] 0.512 0.488
#>
#> $Item_9
#> category_1 category_2
#> P[1 0 0 0] 0.814 0.186
#> P[1 1 0 0] 0.814 0.186
#> P[1 0 1 0] 0.607 0.393
#> P[1 1 1 1] 0.607 0.393
#>
#> $Item_10
#> category_1 category_2
#> P[1 0 0 0] 0.835 0.165
#> P[1 1 0 0] 0.835 0.165
#> P[1 0 1 0] 0.565 0.435
#> P[1 1 1 1] 0.565 0.435
#>
#> $Item_11
#> category_1 category_2
#> P[1 0 0 0] 0.632 0.368
#> P[1 1 0 0] 0.632 0.368
#> P[1 0 1 0] 0.632 0.368
#> P[1 1 1 1] 0.388 0.612
#>
#> $Item_12
#> category_1 category_2
#> P[1 0 0 0] 0.830 0.170
#> P[1 1 0 0] 0.830 0.170
#> P[1 0 1 0] 0.830 0.170
#> P[1 1 1 1] 0.494 0.506
#>
#> $Item_13
#> category_1 category_2
#> P[1 0 0 0] 0.868 0.132
#> P[1 1 0 0] 0.868 0.132
#> P[1 0 1 0] 0.868 0.132
#> P[1 1 1 1] 0.720 0.280
#>
#> $Item_14
#> category_1 category_2
#> P[1 0 0 0] 0.935 0.065
#> P[1 1 0 0] 0.935 0.065
#> P[1 0 1 0] 0.935 0.065
#> P[1 1 1 1] 0.852 0.148
#>
#> $Item_15
#> category_1 category_2
#> P[1 0 0 0] 0.693 0.307
#> P[1 1 0 0] 0.693 0.307
#> P[1 0 1 0] 0.693 0.307
#> P[1 1 1 1] 0.452 0.548
#>
#> $Class.Probability
#> Intercept A1 A2 A1A2 prob
#> Profile_1 1 0 0 0 0.286
#> Profile_2 1 1 0 0 0.107
#> Profile_3 1 0 1 0 0.114
#> Profile_4 1 1 1 1 0.493
#>
M2(DINA) # fits well (as it should)
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR TLI
#> stats 96.49206 87 0.2281074 0.01045052 0 0.02080658 0.02972262 0.9655028
#> CFI
#> stats 0.9714166
cfs <- coef(DINA, simplify=TRUE)$items[11:15,]
cbind(guess, estguess = plogis(cfs[,1]))
#> guess estguess
#> Item_11 0.32210618 0.36762331
#> Item_12 0.21331157 0.17019244
#> Item_13 0.14056317 0.13232904
#> Item_14 0.06866689 0.06517149
#> Item_15 0.28139862 0.30727217
cbind(slip, estslip = 1 - plogis(rowSums(cfs)))
#> slip estslip
#> Item_11 0.3877218 0.3883873
#> Item_12 0.5348058 0.4937323
#> Item_13 0.7359368 0.7203743
#> Item_14 0.8247931 0.8520713
#> Item_15 0.3900682 0.4520799
### DINO model example
theta <- cbind(1, thetaComb(0:1, 2))
# define theta matrix with negative interaction term
(theta <- cbind(theta, -theta[,2] * theta[,3]))
#> [,1] [,2] [,3] [,4]
#> [1,] 1 0 0 0
#> [2,] 1 1 0 0
#> [3,] 1 0 1 0
#> [4,] 1 1 1 -1
model <- mirt.model('Intercept = 1-15
A1 = 1-5, 11-15
A2 = 6-15
Yoshi = 11-15
CONSTRAIN = (11,a2,a3,a4), (12,a2,a3,a4), (13,a2,a3,a4),
(14,a2,a3,a4), (15,a2,a3,a4)')
# last five items are DINOs (first 10 are unidimensional C-RUMs)
DINO <- mdirt(dat, model, customTheta = theta)
coef(DINO, simplify=TRUE)
#> $items
#> a1 a2 a3 a4
#> Item_1 -0.742 -1.825 0.000 0.000
#> Item_2 -0.401 -1.134 0.000 0.000
#> Item_3 -0.548 -3.150 0.000 0.000
#> Item_4 0.580 -2.110 0.000 0.000
#> Item_5 -0.045 -1.616 0.000 0.000
#> Item_6 -2.820 0.000 2.661 0.000
#> Item_7 -1.188 0.000 1.458 0.000
#> Item_8 -1.154 0.000 1.055 0.000
#> Item_9 -1.583 0.000 1.121 0.000
#> Item_10 -1.737 0.000 1.428 0.000
#> Item_11 -0.939 1.164 1.164 1.164
#> Item_12 -1.959 1.579 1.579 1.579
#> Item_13 -2.089 0.915 0.915 0.915
#> Item_14 -3.726 1.852 1.852 1.852
#> Item_15 -1.131 1.075 1.075 1.075
#>
#> $group.intercepts
#> c1 c2 c3
#> par 2.02 1.082 2.941
#>
summary(DINO)
#> $Item_1
#> category_1 category_2
#> P[1 0 0 0] 0.677 0.323
#> P[1 1 0 0] 0.929 0.071
#> P[1 0 1 0] 0.677 0.323
#> P[1 1 1 -1] 0.929 0.071
#>
#> $Item_2
#> category_1 category_2
#> P[1 0 0 0] 0.599 0.401
#> P[1 1 0 0] 0.823 0.177
#> P[1 0 1 0] 0.599 0.401
#> P[1 1 1 -1] 0.823 0.177
#>
#> $Item_3
#> category_1 category_2
#> P[1 0 0 0] 0.634 0.366
#> P[1 1 0 0] 0.976 0.024
#> P[1 0 1 0] 0.634 0.366
#> P[1 1 1 -1] 0.976 0.024
#>
#> $Item_4
#> category_1 category_2
#> P[1 0 0 0] 0.359 0.641
#> P[1 1 0 0] 0.822 0.178
#> P[1 0 1 0] 0.359 0.641
#> P[1 1 1 -1] 0.822 0.178
#>
#> $Item_5
#> category_1 category_2
#> P[1 0 0 0] 0.511 0.489
#> P[1 1 0 0] 0.840 0.160
#> P[1 0 1 0] 0.511 0.489
#> P[1 1 1 -1] 0.840 0.160
#>
#> $Item_6
#> category_1 category_2
#> P[1 0 0 0] 0.944 0.056
#> P[1 1 0 0] 0.944 0.056
#> P[1 0 1 0] 0.540 0.460
#> P[1 1 1 -1] 0.540 0.460
#>
#> $Item_7
#> category_1 category_2
#> P[1 0 0 0] 0.766 0.234
#> P[1 1 0 0] 0.766 0.234
#> P[1 0 1 0] 0.433 0.567
#> P[1 1 1 -1] 0.433 0.567
#>
#> $Item_8
#> category_1 category_2
#> P[1 0 0 0] 0.760 0.240
#> P[1 1 0 0] 0.760 0.240
#> P[1 0 1 0] 0.525 0.475
#> P[1 1 1 -1] 0.525 0.475
#>
#> $Item_9
#> category_1 category_2
#> P[1 0 0 0] 0.830 0.170
#> P[1 1 0 0] 0.830 0.170
#> P[1 0 1 0] 0.613 0.387
#> P[1 1 1 -1] 0.613 0.387
#>
#> $Item_10
#> category_1 category_2
#> P[1 0 0 0] 0.850 0.150
#> P[1 1 0 0] 0.850 0.150
#> P[1 0 1 0] 0.577 0.423
#> P[1 1 1 -1] 0.577 0.423
#>
#> $Item_11
#> category_1 category_2
#> P[1 0 0 0] 0.719 0.281
#> P[1 1 0 0] 0.444 0.556
#> P[1 0 1 0] 0.444 0.556
#> P[1 1 1 -1] 0.444 0.556
#>
#> $Item_12
#> category_1 category_2
#> P[1 0 0 0] 0.876 0.124
#> P[1 1 0 0] 0.594 0.406
#> P[1 0 1 0] 0.594 0.406
#> P[1 1 1 -1] 0.594 0.406
#>
#> $Item_13
#> category_1 category_2
#> P[1 0 0 0] 0.890 0.110
#> P[1 1 0 0] 0.764 0.236
#> P[1 0 1 0] 0.764 0.236
#> P[1 1 1 -1] 0.764 0.236
#>
#> $Item_14
#> category_1 category_2
#> P[1 0 0 0] 0.976 0.024
#> P[1 1 0 0] 0.867 0.133
#> P[1 0 1 0] 0.867 0.133
#> P[1 1 1 -1] 0.867 0.133
#>
#> $Item_15
#> category_1 category_2
#> P[1 0 0 0] 0.756 0.244
#> P[1 1 0 0] 0.514 0.486
#> P[1 0 1 0] 0.514 0.486
#> P[1 1 1 -1] 0.514 0.486
#>
#> $Class.Probability
#> Intercept A1 A2 Yoshi prob
#> Profile_1 1 0 0 0 0.248
#> Profile_2 1 1 0 0 0.097
#> Profile_3 1 0 1 0 0.622
#> Profile_4 1 1 1 -1 0.033
#>
M2(DINO) #doesn't fit as well, because not the generating model
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR
#> stats 146.4856 87 6.92758e-05 0.02616157 0.01856397 0.03336909 0.04139971
#> TLI CFI
#> stats 0.7838103 0.8208714
## C-RUM (analogous to MIRT model)
theta <- cbind(1, thetaComb(0:1, 2))
model <- mirt.model('Intercept = 1-15
A1 = 1-5, 11-15
A2 = 6-15')
CRUM <- mdirt(dat, model, customTheta = theta)
coef(CRUM, simplify=TRUE)
#> $items
#> a1 a2 a3
#> Item_1 -1.405 0.996 0.000
#> Item_2 -0.950 0.876 0.000
#> Item_3 -1.328 1.145 0.000
#> Item_4 -0.235 1.309 0.000
#> Item_5 -0.855 1.342 0.000
#> Item_6 -2.592 0.000 2.479
#> Item_7 -1.095 0.000 1.388
#> Item_8 -1.127 0.000 1.061
#> Item_9 -1.505 0.000 1.058
#> Item_10 -1.674 0.000 1.399
#> Item_11 -0.589 0.491 0.500
#> Item_12 -1.730 1.049 0.743
#> Item_13 -2.052 0.255 0.820
#> Item_14 -3.276 -0.695 1.963
#> Item_15 -0.989 -0.008 1.069
#>
#> $group.intercepts
#> c1 c2 c3
#> par -0.225 -2.397 -0.726
#>
summary(CRUM)
#> $Item_1
#> category_1 category_2
#> P[1 0 0] 0.803 0.197
#> P[1 1 0] 0.601 0.399
#> P[1 0 1] 0.803 0.197
#> P[1 1 1] 0.601 0.399
#>
#> $Item_2
#> category_1 category_2
#> P[1 0 0] 0.721 0.279
#> P[1 1 0] 0.519 0.481
#> P[1 0 1] 0.721 0.279
#> P[1 1 1] 0.519 0.481
#>
#> $Item_3
#> category_1 category_2
#> P[1 0 0] 0.791 0.209
#> P[1 1 0] 0.546 0.454
#> P[1 0 1] 0.791 0.209
#> P[1 1 1] 0.546 0.454
#>
#> $Item_4
#> category_1 category_2
#> P[1 0 0] 0.559 0.441
#> P[1 1 0] 0.255 0.745
#> P[1 0 1] 0.559 0.441
#> P[1 1 1] 0.255 0.745
#>
#> $Item_5
#> category_1 category_2
#> P[1 0 0] 0.702 0.298
#> P[1 1 0] 0.381 0.619
#> P[1 0 1] 0.702 0.298
#> P[1 1 1] 0.381 0.619
#>
#> $Item_6
#> category_1 category_2
#> P[1 0 0] 0.930 0.070
#> P[1 1 0] 0.930 0.070
#> P[1 0 1] 0.528 0.472
#> P[1 1 1] 0.528 0.472
#>
#> $Item_7
#> category_1 category_2
#> P[1 0 0] 0.749 0.251
#> P[1 1 0] 0.749 0.251
#> P[1 0 1] 0.427 0.573
#> P[1 1 1] 0.427 0.573
#>
#> $Item_8
#> category_1 category_2
#> P[1 0 0] 0.755 0.245
#> P[1 1 0] 0.755 0.245
#> P[1 0 1] 0.517 0.483
#> P[1 1 1] 0.517 0.483
#>
#> $Item_9
#> category_1 category_2
#> P[1 0 0] 0.818 0.182
#> P[1 1 0] 0.818 0.182
#> P[1 0 1] 0.610 0.390
#> P[1 1 1] 0.610 0.390
#>
#> $Item_10
#> category_1 category_2
#> P[1 0 0] 0.842 0.158
#> P[1 1 0] 0.842 0.158
#> P[1 0 1] 0.568 0.432
#> P[1 1 1] 0.568 0.432
#>
#> $Item_11
#> category_1 category_2
#> P[1 0 0] 0.643 0.357
#> P[1 1 0] 0.525 0.475
#> P[1 0 1] 0.522 0.478
#> P[1 1 1] 0.401 0.599
#>
#> $Item_12
#> category_1 category_2
#> P[1 0 0] 0.849 0.151
#> P[1 1 0] 0.664 0.336
#> P[1 0 1] 0.729 0.271
#> P[1 1 1] 0.485 0.515
#>
#> $Item_13
#> category_1 category_2
#> P[1 0 0] 0.886 0.114
#> P[1 1 0] 0.858 0.142
#> P[1 0 1] 0.774 0.226
#> P[1 1 1] 0.727 0.273
#>
#> $Item_14
#> category_1 category_2
#> P[1 0 0] 0.964 0.036
#> P[1 1 0] 0.981 0.019
#> P[1 0 1] 0.788 0.212
#> P[1 1 1] 0.882 0.118
#>
#> $Item_15
#> category_1 category_2
#> P[1 0 0] 0.729 0.271
#> P[1 1 0] 0.730 0.270
#> P[1 0 1] 0.480 0.520
#> P[1 1 1] 0.482 0.518
#>
#> $Class.Probability
#> Intercept A1 A2 prob
#> Profile_1 1 0 0 0.337
#> Profile_2 1 1 0 0.038
#> Profile_3 1 0 1 0.204
#> Profile_4 1 1 1 0.421
#>
# good fit, but over-saturated (main effects for items 11-15 can be set to 0)
M2(CRUM)
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR TLI
#> stats 85.54849 82 0.3725545 0.006581614 0 0.01905772 0.02788709 0.9863173
#> CFI
#> stats 0.9893145
#------------------
# multidimensional latent class model
dat <- key2binary(SAT12,
key = c(1,4,5,2,3,1,2,1,3,1,2,4,2,1,5,3,4,4,1,4,3,3,4,1,3,5,1,3,1,5,4,5))
# 5 latent classes within 2 different sets of items
model <- mirt.model('C1 = 1-16
C2 = 1-16
C3 = 1-16
C4 = 1-16
C5 = 1-16
C6 = 17-32
C7 = 17-32
C8 = 17-32
C9 = 17-32
C10 = 17-32
CONSTRAIN = (1-16, a1), (1-16, a2), (1-16, a3), (1-16, a4), (1-16, a5),
(17-32, a6), (17-32, a7), (17-32, a8), (17-32, a9), (17-32, a10)')
theta <- diag(10) # defined explicitly. Otherwise, this profile is assumed
mod <- mdirt(dat, model, customTheta = theta)
coef(mod, simplify=TRUE)
#> $items
#> a1 a2 a3 a4 a5 a6 a7 a8 a9 a10
#> Item.1 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.2 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.3 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.4 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.5 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.6 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.7 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.8 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.9 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.10 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.11 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.12 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.13 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.14 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.15 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.16 -0.928 -0.682 -0.574 -0.541 -0.365 0.000 0.000 0.000 0.000 0.00
#> Item.17 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.18 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.19 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.20 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.21 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.22 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.23 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.24 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.25 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.26 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.27 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.28 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.29 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.30 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.31 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#> Item.32 0.000 0.000 0.000 0.000 0.000 0.309 0.445 1.389 1.396 1.42
#>
#> $group.intercepts
#> c1 c2 c3 c4 c5 c6 c7 c8 c9
#> par -2.737 -1.479 0.135 1.486 2.186 2.884 2.316 2.146 1.112
#>
summary(mod)
#> $Item.1
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.2
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.3
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.4
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.5
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.6
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.7
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.8
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.9
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.10
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.11
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.12
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.13
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.14
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.15
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.16
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.717 0.283
#> P[0 1 0 0 0 0 0 0 0 0] 0.664 0.336
#> P[0 0 1 0 0 0 0 0 0 0] 0.640 0.360
#> P[0 0 0 1 0 0 0 0 0 0] 0.632 0.368
#> P[0 0 0 0 1 0 0 0 0 0] 0.590 0.410
#> P[0 0 0 0 0 1 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 1 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 1 0 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 1 0] 0.500 0.500
#> P[0 0 0 0 0 0 0 0 0 1] 0.500 0.500
#>
#> $Item.17
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.18
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.19
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.20
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.21
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.22
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.23
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.24
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.25
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.26
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.27
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.28
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.29
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.30
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.31
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Item.32
#> category_1 category_2
#> P[1 0 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 1 0 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 1 0 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 1 0 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 1 0 0 0 0 0] 0.500 0.500
#> P[0 0 0 0 0 1 0 0 0 0] 0.423 0.577
#> P[0 0 0 0 0 0 1 0 0 0] 0.391 0.609
#> P[0 0 0 0 0 0 0 1 0 0] 0.200 0.800
#> P[0 0 0 0 0 0 0 0 1 0] 0.198 0.802
#> P[0 0 0 0 0 0 0 0 0 1] 0.195 0.805
#>
#> $Class.Probability
#> C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 prob
#> Profile_1 1 0 0 0 0 0 0 0 0 0 0.001
#> Profile_2 0 1 0 0 0 0 0 0 0 0 0.004
#> Profile_3 0 0 1 0 0 0 0 0 0 0 0.021
#> Profile_4 0 0 0 1 0 0 0 0 0 0 0.080
#> Profile_5 0 0 0 0 1 0 0 0 0 0 0.161
#> Profile_6 0 0 0 0 0 1 0 0 0 0 0.323
#> Profile_7 0 0 0 0 0 0 1 0 0 0 0.183
#> Profile_8 0 0 0 0 0 0 0 1 0 0 0.154
#> Profile_9 0 0 0 0 0 0 0 0 1 0 0.055
#> Profile_10 0 0 0 0 0 0 0 0 0 1 0.018
#>
#------------------
# multiple group with constrained group probabilities
dat <- key2binary(SAT12,
key = c(1,4,5,2,3,1,2,1,3,1,2,4,2,1,5,3,4,4,1,4,3,3,4,1,3,5,1,3,1,5,4,5))
group <- rep(c('G1', 'G2'), each = nrow(SAT12)/2)
Theta <- diag(2)
# the latent class parameters are technically located in the (nitems + 1) location
model <- mirt.model('A1 = 1-32
A2 = 1-32
CONSTRAINB = (33, c1)')
mod <- mdirt(dat, model, group = group, customTheta = Theta)
coef(mod, simplify=TRUE)
#> $G1
#> $items
#> a1 a2
#> Item.1 -1.462 -0.238
#> Item.2 -0.521 1.906
#> Item.3 -1.638 -0.086
#> Item.4 -1.181 0.115
#> Item.5 -0.148 1.966
#> Item.6 -2.913 -1.119
#> Item.7 0.469 2.108
#> Item.8 -1.833 -0.731
#> Item.9 1.888 2.722
#> Item.10 -0.972 0.381
#> Item.11 4.483 9.736
#> Item.12 -0.381 -0.305
#> Item.13 0.008 1.822
#> Item.14 0.411 2.340
#> Item.15 0.737 3.361
#> Item.16 -0.997 0.142
#> Item.17 2.649 4.629
#> Item.18 -1.588 0.583
#> Item.19 -0.414 1.057
#> Item.20 1.254 4.568
#> Item.21 1.959 3.170
#> Item.22 1.966 9.258
#> Item.23 -1.633 -0.393
#> Item.24 0.271 2.351
#> Item.25 -1.224 0.329
#> Item.26 -0.973 1.198
#> Item.27 1.152 9.497
#> Item.28 -0.477 1.177
#> Item.29 -1.235 0.072
#> Item.30 -0.514 0.150
#> Item.31 0.762 9.508
#> Item.32 -1.381 -1.742
#>
#> $group.intercepts
#> c1
#> par 0.417
#>
#>
#> $G2
#> $items
#> a1 a2
#> Item.1 -1.384 -0.425
#> Item.2 -0.489 1.722
#> Item.3 -1.885 -0.060
#> Item.4 -0.826 0.229
#> Item.5 0.002 1.268
#> Item.6 -2.386 -0.599
#> Item.7 0.857 2.671
#> Item.8 -1.887 -0.940
#> Item.9 1.628 2.612
#> Item.10 -1.045 0.944
#> Item.11 3.083 9.624
#> Item.12 -0.487 -0.108
#> Item.13 0.252 1.769
#> Item.14 0.382 2.386
#> Item.15 1.234 2.787
#> Item.16 -0.739 0.608
#> Item.17 2.960 9.577
#> Item.18 -1.967 0.785
#> Item.19 -0.234 1.067
#> Item.20 1.455 5.466
#> Item.21 2.272 2.768
#> Item.22 2.282 6.782
#> Item.23 -1.106 0.203
#> Item.24 0.554 2.569
#> Item.25 -0.868 0.046
#> Item.26 -1.271 1.392
#> Item.27 1.382 3.530
#> Item.28 -0.605 1.314
#> Item.29 -1.390 0.202
#> Item.30 -0.475 0.113
#> Item.31 1.209 4.734
#> Item.32 -2.028 -1.480
#>
#> $group.intercepts
#> c1
#> par 0.417
#>
#>
summary(mod)
#> $G1
#> $Item.1
#> category_1 category_2
#> P[1 0] 0.812 0.188
#> P[0 1] 0.559 0.441
#>
#> $Item.2
#> category_1 category_2
#> P[1 0] 0.627 0.373
#> P[0 1] 0.129 0.871
#>
#> $Item.3
#> category_1 category_2
#> P[1 0] 0.837 0.163
#> P[0 1] 0.522 0.478
#>
#> $Item.4
#> category_1 category_2
#> P[1 0] 0.765 0.235
#> P[0 1] 0.471 0.529
#>
#> $Item.5
#> category_1 category_2
#> P[1 0] 0.537 0.463
#> P[0 1] 0.123 0.877
#>
#> $Item.6
#> category_1 category_2
#> P[1 0] 0.949 0.051
#> P[0 1] 0.754 0.246
#>
#> $Item.7
#> category_1 category_2
#> P[1 0] 0.385 0.615
#> P[0 1] 0.108 0.892
#>
#> $Item.8
#> category_1 category_2
#> P[1 0] 0.862 0.138
#> P[0 1] 0.675 0.325
#>
#> $Item.9
#> category_1 category_2
#> P[1 0] 0.131 0.869
#> P[0 1] 0.062 0.938
#>
#> $Item.10
#> category_1 category_2
#> P[1 0] 0.726 0.274
#> P[0 1] 0.406 0.594
#>
#> $Item.11
#> category_1 category_2
#> P[1 0] 0.011 0.989
#> P[0 1] 0.000 1.000
#>
#> $Item.12
#> category_1 category_2
#> P[1 0] 0.594 0.406
#> P[0 1] 0.576 0.424
#>
#> $Item.13
#> category_1 category_2
#> P[1 0] 0.498 0.502
#> P[0 1] 0.139 0.861
#>
#> $Item.14
#> category_1 category_2
#> P[1 0] 0.399 0.601
#> P[0 1] 0.088 0.912
#>
#> $Item.15
#> category_1 category_2
#> P[1 0] 0.324 0.676
#> P[0 1] 0.034 0.966
#>
#> $Item.16
#> category_1 category_2
#> P[1 0] 0.731 0.269
#> P[0 1] 0.465 0.535
#>
#> $Item.17
#> category_1 category_2
#> P[1 0] 0.066 0.934
#> P[0 1] 0.010 0.990
#>
#> $Item.18
#> category_1 category_2
#> P[1 0] 0.830 0.170
#> P[0 1] 0.358 0.642
#>
#> $Item.19
#> category_1 category_2
#> P[1 0] 0.602 0.398
#> P[0 1] 0.258 0.742
#>
#> $Item.20
#> category_1 category_2
#> P[1 0] 0.222 0.778
#> P[0 1] 0.010 0.990
#>
#> $Item.21
#> category_1 category_2
#> P[1 0] 0.124 0.876
#> P[0 1] 0.040 0.960
#>
#> $Item.22
#> category_1 category_2
#> P[1 0] 0.123 0.877
#> P[0 1] 0.000 1.000
#>
#> $Item.23
#> category_1 category_2
#> P[1 0] 0.837 0.163
#> P[0 1] 0.597 0.403
#>
#> $Item.24
#> category_1 category_2
#> P[1 0] 0.433 0.567
#> P[0 1] 0.087 0.913
#>
#> $Item.25
#> category_1 category_2
#> P[1 0] 0.773 0.227
#> P[0 1] 0.419 0.581
#>
#> $Item.26
#> category_1 category_2
#> P[1 0] 0.726 0.274
#> P[0 1] 0.232 0.768
#>
#> $Item.27
#> category_1 category_2
#> P[1 0] 0.24 0.76
#> P[0 1] 0.00 1.00
#>
#> $Item.28
#> category_1 category_2
#> P[1 0] 0.617 0.383
#> P[0 1] 0.236 0.764
#>
#> $Item.29
#> category_1 category_2
#> P[1 0] 0.775 0.225
#> P[0 1] 0.482 0.518
#>
#> $Item.30
#> category_1 category_2
#> P[1 0] 0.626 0.374
#> P[0 1] 0.463 0.537
#>
#> $Item.31
#> category_1 category_2
#> P[1 0] 0.318 0.682
#> P[0 1] 0.000 1.000
#>
#> $Item.32
#> category_1 category_2
#> P[1 0] 0.799 0.201
#> P[0 1] 0.851 0.149
#>
#> $Class.Probability
#> A1 A2 prob
#> Profile_1 1 0 0.603
#> Profile_2 0 1 0.397
#>
#>
#> $G2
#> $Item.1
#> category_1 category_2
#> P[1 0] 0.800 0.200
#> P[0 1] 0.605 0.395
#>
#> $Item.2
#> category_1 category_2
#> P[1 0] 0.620 0.380
#> P[0 1] 0.152 0.848
#>
#> $Item.3
#> category_1 category_2
#> P[1 0] 0.868 0.132
#> P[0 1] 0.515 0.485
#>
#> $Item.4
#> category_1 category_2
#> P[1 0] 0.695 0.305
#> P[0 1] 0.443 0.557
#>
#> $Item.5
#> category_1 category_2
#> P[1 0] 0.499 0.501
#> P[0 1] 0.220 0.780
#>
#> $Item.6
#> category_1 category_2
#> P[1 0] 0.916 0.084
#> P[0 1] 0.645 0.355
#>
#> $Item.7
#> category_1 category_2
#> P[1 0] 0.298 0.702
#> P[0 1] 0.065 0.935
#>
#> $Item.8
#> category_1 category_2
#> P[1 0] 0.868 0.132
#> P[0 1] 0.719 0.281
#>
#> $Item.9
#> category_1 category_2
#> P[1 0] 0.164 0.836
#> P[0 1] 0.068 0.932
#>
#> $Item.10
#> category_1 category_2
#> P[1 0] 0.74 0.26
#> P[0 1] 0.28 0.72
#>
#> $Item.11
#> category_1 category_2
#> P[1 0] 0.044 0.956
#> P[0 1] 0.000 1.000
#>
#> $Item.12
#> category_1 category_2
#> P[1 0] 0.619 0.381
#> P[0 1] 0.527 0.473
#>
#> $Item.13
#> category_1 category_2
#> P[1 0] 0.437 0.563
#> P[0 1] 0.146 0.854
#>
#> $Item.14
#> category_1 category_2
#> P[1 0] 0.406 0.594
#> P[0 1] 0.084 0.916
#>
#> $Item.15
#> category_1 category_2
#> P[1 0] 0.226 0.774
#> P[0 1] 0.058 0.942
#>
#> $Item.16
#> category_1 category_2
#> P[1 0] 0.677 0.323
#> P[0 1] 0.352 0.648
#>
#> $Item.17
#> category_1 category_2
#> P[1 0] 0.049 0.951
#> P[0 1] 0.000 1.000
#>
#> $Item.18
#> category_1 category_2
#> P[1 0] 0.877 0.123
#> P[0 1] 0.313 0.687
#>
#> $Item.19
#> category_1 category_2
#> P[1 0] 0.558 0.442
#> P[0 1] 0.256 0.744
#>
#> $Item.20
#> category_1 category_2
#> P[1 0] 0.189 0.811
#> P[0 1] 0.004 0.996
#>
#> $Item.21
#> category_1 category_2
#> P[1 0] 0.093 0.907
#> P[0 1] 0.059 0.941
#>
#> $Item.22
#> category_1 category_2
#> P[1 0] 0.093 0.907
#> P[0 1] 0.001 0.999
#>
#> $Item.23
#> category_1 category_2
#> P[1 0] 0.751 0.249
#> P[0 1] 0.449 0.551
#>
#> $Item.24
#> category_1 category_2
#> P[1 0] 0.365 0.635
#> P[0 1] 0.071 0.929
#>
#> $Item.25
#> category_1 category_2
#> P[1 0] 0.704 0.296
#> P[0 1] 0.489 0.511
#>
#> $Item.26
#> category_1 category_2
#> P[1 0] 0.781 0.219
#> P[0 1] 0.199 0.801
#>
#> $Item.27
#> category_1 category_2
#> P[1 0] 0.201 0.799
#> P[0 1] 0.028 0.972
#>
#> $Item.28
#> category_1 category_2
#> P[1 0] 0.647 0.353
#> P[0 1] 0.212 0.788
#>
#> $Item.29
#> category_1 category_2
#> P[1 0] 0.801 0.199
#> P[0 1] 0.450 0.550
#>
#> $Item.30
#> category_1 category_2
#> P[1 0] 0.617 0.383
#> P[0 1] 0.472 0.528
#>
#> $Item.31
#> category_1 category_2
#> P[1 0] 0.230 0.770
#> P[0 1] 0.009 0.991
#>
#> $Item.32
#> category_1 category_2
#> P[1 0] 0.884 0.116
#> P[0 1] 0.815 0.185
#>
#> $Class.Probability
#> A1 A2 prob
#> Profile_1 1 0 0.603
#> Profile_2 0 1 0.397
#>
#>
#------------------
# Probabilistic Guttman Model (Proctor, 1970)
# example analysis can also be found in the sirt package (see ?prob.guttman)
data(data.read, package = 'sirt')
head(data.read)
#> A1 A2 A3 A4 B1 B2 B3 B4 C1 C2 C3 C4
#> 2 1 1 1 1 1 1 1 1 1 1 1 0
#> 22 1 1 0 0 1 0 1 1 1 0 1 0
#> 23 1 1 0 1 1 0 1 1 1 1 1 1
#> 41 1 1 1 1 1 1 1 1 1 1 1 1
#> 43 1 0 0 1 0 0 1 1 1 0 1 0
#> 63 1 1 0 0 1 0 1 1 1 1 1 1
Theta <- matrix(c(1,0,0,0,
1,1,0,0,
1,1,1,0,
1,1,1,1), 4, byrow=TRUE)
model <- mirt.model("INTERCEPT = 1-12
C1 = 1,7,9,11
C2 = 2,5,8,10,12
C3 = 3,4,6")
mod <- mdirt(data.read, model, customTheta=Theta)
summary(mod)
#> $A1
#> category_1 category_2
#> P[1 0 0 0] 0.331 0.669
#> P[1 1 0 0] 0.037 0.963
#> P[1 1 1 0] 0.037 0.963
#> P[1 1 1 1] 0.037 0.963
#>
#> $A2
#> category_1 category_2
#> P[1 0 0 0] 0.544 0.456
#> P[1 1 0 0] 0.544 0.456
#> P[1 1 1 0] 0.041 0.959
#> P[1 1 1 1] 0.041 0.959
#>
#> $A3
#> category_1 category_2
#> P[1 0 0 0] 0.687 0.313
#> P[1 1 0 0] 0.687 0.313
#> P[1 1 1 0] 0.687 0.313
#> P[1 1 1 1] 0.097 0.903
#>
#> $A4
#> category_1 category_2
#> P[1 0 0 0] 0.709 0.291
#> P[1 1 0 0] 0.709 0.291
#> P[1 1 1 0] 0.709 0.291
#> P[1 1 1 1] 0.315 0.685
#>
#> $B1
#> category_1 category_2
#> P[1 0 0 0] 0.438 0.562
#> P[1 1 0 0] 0.438 0.562
#> P[1 1 1 0] 0.168 0.832
#> P[1 1 1 1] 0.168 0.832
#>
#> $B2
#> category_1 category_2
#> P[1 0 0 0] 0.628 0.372
#> P[1 1 0 0] 0.628 0.372
#> P[1 1 1 0] 0.628 0.372
#> P[1 1 1 1] 0.317 0.683
#>
#> $B3
#> category_1 category_2
#> P[1 0 0 0] 0.205 0.795
#> P[1 1 0 0] 0.021 0.979
#> P[1 1 1 0] 0.021 0.979
#> P[1 1 1 1] 0.021 0.979
#>
#> $B4
#> category_1 category_2
#> P[1 0 0 0] 0.543 0.457
#> P[1 1 0 0] 0.543 0.457
#> P[1 1 1 0] 0.140 0.860
#> P[1 1 1 1] 0.140 0.860
#>
#> $C1
#> category_1 category_2
#> P[1 0 0 0] 0.175 0.825
#> P[1 1 0 0] 0.000 1.000
#> P[1 1 1 0] 0.000 1.000
#> P[1 1 1 1] 0.000 1.000
#>
#> $C2
#> category_1 category_2
#> P[1 0 0 0] 0.526 0.474
#> P[1 1 0 0] 0.526 0.474
#> P[1 1 1 0] 0.098 0.902
#> P[1 1 1 1] 0.098 0.902
#>
#> $C3
#> category_1 category_2
#> P[1 0 0 0] 0.292 0.708
#> P[1 1 0 0] 0.026 0.974
#> P[1 1 1 0] 0.026 0.974
#> P[1 1 1 1] 0.026 0.974
#>
#> $C4
#> category_1 category_2
#> P[1 0 0 0] 0.425 0.575
#> P[1 1 0 0] 0.425 0.575
#> P[1 1 1 0] 0.140 0.860
#> P[1 1 1 1] 0.140 0.860
#>
#> $Class.Probability
#> INTERCEPT C1 C2 C3 prob
#> Profile_1 1 0 0 0 0.383
#> Profile_2 1 1 0 0 0.057
#> Profile_3 1 1 1 0 0.130
#> Profile_4 1 1 1 1 0.431
#>
M2(mod)
#> M2 df p RMSEA RMSEA_5 RMSEA_95 SRMSR
#> stats 145.0553 51 5.876977e-11 0.07509875 0.06080295 0.08947343 0.09158964
#> TLI CFI
#> stats 0.8130941 0.8555727
itemfit(mod)
#> item S_X2 df.S_X2 RMSEA.S_X2 p.S_X2
#> 1 A1 27.808 7 0.095 0.000
#> 2 A2 2.984 6 0.000 0.811
#> 3 A3 10.219 6 0.046 0.116
#> 4 A4 5.575 6 0.000 0.472
#> 5 B1 8.168 7 0.023 0.318
#> 6 B2 7.176 6 0.024 0.305
#> 7 B3 9.351 7 0.032 0.228
#> 8 B4 2.359 6 0.000 0.884
#> 9 C1 6.260 5 0.028 0.282
#> 10 C2 6.914 6 0.022 0.329
#> 11 C3 11.734 7 0.045 0.110
#> 12 C4 5.585 7 0.000 0.589
# }