Skip to contents

Probabilistic Bisection Algorithm

Source: R/PBA.R
PBA.Rd

The function PBA searches a specified interval for a root (i.e., zero) of the function f(x) with respect to its first argument. However, this function differs from deterministic cousins such as uniroot in that f may contain stochastic error components, and instead provides a Bayesian interval where the root is likely to lie. Note that it is assumed that E[f(x)] is non-decreasing in x and that the root is between the search interval (evaluated approximately when check.interval=TRUE). See Waeber, Frazier, and Henderson (2013) for details.

Usage

PBA(
  f,
  interval,
  ...,
  p = 0.6,
  integer = FALSE,
  tol = if (integer) 0.01 else 1e-04,
  maxiter = 300L,
  miniter = 100L,
  wait.time = NULL,
  f.prior = NULL,
  resolution = 10000L,
  check.interval = TRUE,
  check.interval.only = FALSE,
  verbose = TRUE
)

# S3 method for class 'PBA'
print(x, ...)

# S3 method for class 'PBA'
plot(x, type = "posterior", main = "Probabilistic Bisection Posterior", ...)

Arguments

f

noisy function for which the root is sought

interval

a vector containing the end-points of the interval to be searched for the root

...

additional named arguments to be passed to f

p

assumed constant for probability of correct responses (must be > 0.5)

integer

logical; should the values of the root be considered integer or numeric? The former uses a discreet grid to track the updates, while the latter currently creates a grid with resolution points

tol

tolerance criteria for convergence based on average of the f(x) evaluations

maxiter

the maximum number of iterations (default 300)

miniter

minimum number of iterations (default 100)

wait.time

(optional) instead of terminating after specific estimate criteria are satisfied (e.g., tol), terminate after a specific wait time. Input is specified either as a numeric vector in seconds or as a character vector to be formatted by timeFormater. Note that users should increase the number of maxiter as well so that termination can occur if either the maximum iterations are satisfied or the specified wait time has elapsed (whichever occurs first)

f.prior

density function indicating the likely location of the prior (e.g., if root is within [0,1] then dunif works, otherwise custom functions will be required)

resolution

constant indicating the number of equally spaced grid points to track when integer = FALSE.

check.interval

logical; should an initial check be made to determine whether f(interval[1L]) and f(interval[2L]) have opposite signs? Default is TRUE

check.interval.only

logical; return only TRUE or FALSE to test whether there is a likely root given interval? Setting this to TRUE can be useful when you are unsure about the root location interval and may want to use a higher replication input from SimSolve

verbose

logical; should the iterations and estimate be printed to the console?

x

an object of class PBA

type

type of plot to draw for PBA object. Can be either 'posterior' or 'history' to plot the PBA posterior distribution or the mediation iteration history

main

plot title

References

Horstein, M. (1963). Sequential transmission using noiseless feedback. IEEE Trans. Inform. Theory, 9(3):136-143.

Waeber, R., Frazier, P. I. & Henderson, S. G. (2013). Bisection Search with Noisy Responses. SIAM Journal on Control and Optimization, Society for Industrial & Applied Mathematics (SIAM), 51, 2261-2279.

See also

uniroot, RobbinsMonro

Examples


# find x that solves f(x) - b = 0 for the following
f.root <- function(x, b = .6) 1 / (1 + exp(-x)) - b
f.root(.3)
#> [1] -0.02555748

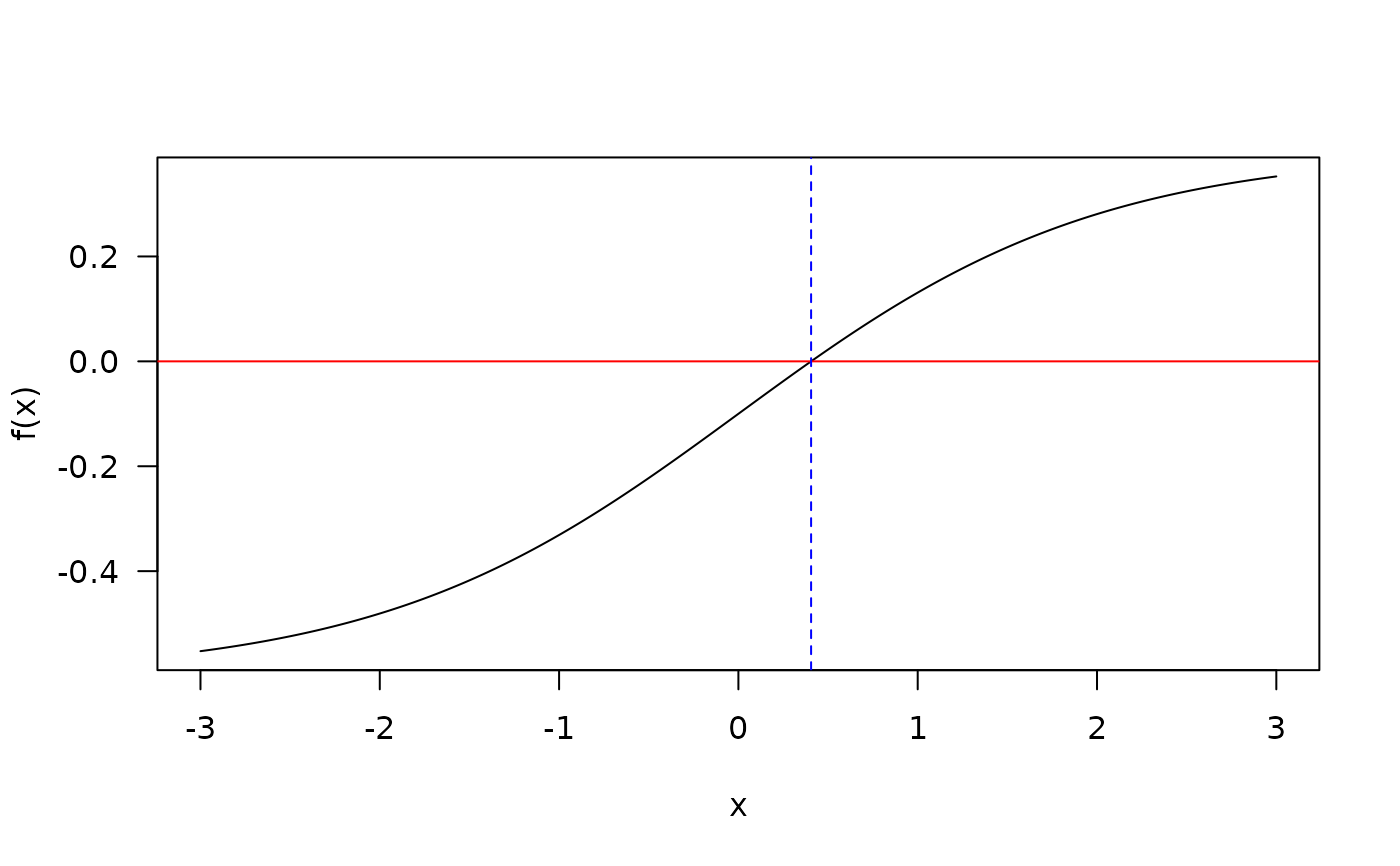
xs <- seq(-3,3, length.out=1000)
plot(xs, f.root(xs), type = 'l', ylab = "f(x)", xlab='x', las=1)
abline(h=0, col='red')

retuni <- uniroot(f.root, c(0,1))
retuni
#> $root
#> [1] 0.4054644
#> 
#> $f.root
#> [1] -1.772764e-07
#> 
#> $iter
#> [1] 4
#> 
#> $init.it
#> [1] NA
#> 
#> $estim.prec
#> [1] 6.103516e-05
#> 
abline(v=retuni$root, col='blue', lty=2)


# PBA without noisy root
retpba <- PBA(f.root, c(0,1))
#> 
Iter: 1; Median = 0.500; E(f(x)) = 0.02
Iter: 2; Median = 0.417; E(f(x)) = 0.01
Iter: 3; Median = 0.347; E(f(x)) = 0.00
Iter: 4; Median = 0.405; E(f(x)) = 0.00
Iter: 5; Median = 0.472; E(f(x)) = 0.01
Iter: 6; Median = 0.413; E(f(x)) = 0.00
Iter: 7; Median = 0.367; E(f(x)) = 0.00
Iter: 8; Median = 0.407; E(f(x)) = 0.00
Iter: 9; Median = 0.374; E(f(x)) = 0.00
Iter: 10; Median = 0.403; E(f(x)) = 0.00
Iter: 11; Median = 0.440; E(f(x)) = 0.00
Iter: 12; Median = 0.406; E(f(x)) = 0.00
Iter: 13; Median = 0.384; E(f(x)) = 0.00
Iter: 14; Median = 0.404; E(f(x)) = 0.00
Iter: 15; Median = 0.425; E(f(x)) = 0.00
Iter: 16; Median = 0.406; E(f(x)) = 0.00
Iter: 17; Median = 0.391; E(f(x)) = 0.00
Iter: 18; Median = 0.405; E(f(x)) = 0.00
Iter: 19; Median = 0.415; E(f(x)) = 0.00
Iter: 20; Median = 0.406; E(f(x)) = 0.00
Iter: 21; Median = 0.396; E(f(x)) = 0.00
Iter: 22; Median = 0.405; E(f(x)) = 0.00
Iter: 23; Median = 0.410; E(f(x)) = 0.00
Iter: 24; Median = 0.405; E(f(x)) = 0.00
Iter: 25; Median = 0.409; E(f(x)) = 0.00
Iter: 26; Median = 0.405; E(f(x)) = 0.00
Iter: 27; Median = 0.408; E(f(x)) = 0.00
Iter: 28; Median = 0.406; E(f(x)) = 0.00
Iter: 29; Median = 0.404; E(f(x)) = 0.00
Iter: 30; Median = 0.406; E(f(x)) = 0.00
Iter: 31; Median = 0.404; E(f(x)) = 0.00
Iter: 32; Median = 0.405; E(f(x)) = 0.00
Iter: 33; Median = 0.406; E(f(x)) = 0.00
Iter: 34; Median = 0.406; E(f(x)) = 0.00
Iter: 35; Median = 0.405; E(f(x)) = 0.00
Iter: 36; Median = 0.406; E(f(x)) = 0.00
Iter: 37; Median = 0.405; E(f(x)) = 0.00
Iter: 38; Median = 0.405; E(f(x)) = 0.00
Iter: 39; Median = 0.406; E(f(x)) = 0.00
Iter: 40; Median = 0.406; E(f(x)) = 0.00
Iter: 41; Median = 0.405; E(f(x)) = 0.00
Iter: 42; Median = 0.406; E(f(x)) = 0.00
Iter: 43; Median = 0.405; E(f(x)) = 0.00
Iter: 44; Median = 0.405; E(f(x)) = 0.00
Iter: 45; Median = 0.406; E(f(x)) = 0.00
Iter: 46; Median = 0.405; E(f(x)) = 0.00
Iter: 47; Median = 0.406; E(f(x)) = 0.00
Iter: 48; Median = 0.406; E(f(x)) = 0.00
Iter: 49; Median = 0.406; E(f(x)) = 0.00
Iter: 50; Median = 0.406; E(f(x)) = 0.00
Iter: 51; Median = 0.405; E(f(x)) = 0.00
Iter: 52; Median = 0.405; E(f(x)) = 0.00
Iter: 53; Median = 0.406; E(f(x)) = 0.00
Iter: 54; Median = 0.406; E(f(x)) = 0.00
Iter: 55; Median = 0.405; E(f(x)) = 0.00
Iter: 56; Median = 0.406; E(f(x)) = 0.00
Iter: 57; Median = 0.405; E(f(x)) = 0.00
Iter: 58; Median = 0.405; E(f(x)) = 0.00
Iter: 59; Median = 0.405; E(f(x)) = 0.00
Iter: 60; Median = 0.406; E(f(x)) = 0.00
Iter: 61; Median = 0.405; E(f(x)) = 0.00
Iter: 62; Median = 0.406; E(f(x)) = 0.00
Iter: 63; Median = 0.406; E(f(x)) = 0.00
Iter: 64; Median = 0.405; E(f(x)) = 0.00
Iter: 65; Median = 0.406; E(f(x)) = 0.00
Iter: 66; Median = 0.406; E(f(x)) = 0.00
Iter: 67; Median = 0.405; E(f(x)) = 0.00
Iter: 68; Median = 0.405; E(f(x)) = 0.00
Iter: 69; Median = 0.406; E(f(x)) = 0.00
Iter: 70; Median = 0.406; E(f(x)) = 0.00
Iter: 71; Median = 0.406; E(f(x)) = 0.00
Iter: 72; Median = 0.406; E(f(x)) = 0.00
Iter: 73; Median = 0.406; E(f(x)) = 0.00
Iter: 74; Median = 0.405; E(f(x)) = 0.00
Iter: 75; Median = 0.406; E(f(x)) = 0.00
Iter: 76; Median = 0.405; E(f(x)) = 0.00
Iter: 77; Median = 0.406; E(f(x)) = 0.00
Iter: 78; Median = 0.405; E(f(x)) = 0.00
Iter: 79; Median = 0.405; E(f(x)) = 0.00
Iter: 80; Median = 0.405; E(f(x)) = 0.00
Iter: 81; Median = 0.405; E(f(x)) = 0.00
Iter: 82; Median = 0.406; E(f(x)) = 0.00
Iter: 83; Median = 0.406; E(f(x)) = 0.00
Iter: 84; Median = 0.406; E(f(x)) = 0.00
Iter: 85; Median = 0.406; E(f(x)) = 0.00
Iter: 86; Median = 0.406; E(f(x)) = 0.00
Iter: 87; Median = 0.406; E(f(x)) = 0.00
Iter: 88; Median = 0.406; E(f(x)) = 0.00
Iter: 89; Median = 0.406; E(f(x)) = 0.00
Iter: 90; Median = 0.406; E(f(x)) = 0.00
Iter: 91; Median = 0.406; E(f(x)) = 0.00
Iter: 92; Median = 0.406; E(f(x)) = 0.00
Iter: 93; Median = 0.406; E(f(x)) = 0.00
Iter: 94; Median = 0.405; E(f(x)) = 0.00
Iter: 95; Median = 0.406; E(f(x)) = 0.00
Iter: 96; Median = 0.406; E(f(x)) = 0.00
Iter: 97; Median = 0.406; E(f(x)) = 0.00
Iter: 98; Median = 0.406; E(f(x)) = 0.00
Iter: 99; Median = 0.405; E(f(x)) = 0.00
Iter: 100; Median = 0.406; E(f(x)) = 0.00
Iter: 101; Median = 0.405; E(f(x)) = 0.00
Iter: 102; Median = 0.405; E(f(x)) = 0.00
Iter: 103; Median = 0.405; E(f(x)) = 0.00
Iter: 104; Median = 0.405; E(f(x)) = 0.00
Iter: 105; Median = 0.406; E(f(x)) = 0.00
Iter: 106; Median = 0.406; E(f(x)) = 0.00
Iter: 107; Median = 0.406; E(f(x)) = 0.00
Iter: 108; Median = 0.405; E(f(x)) = 0.00
Iter: 109; Median = 0.405; E(f(x)) = 0.00
Iter: 110; Median = 0.405; E(f(x)) = 0.00
Iter: 111; Median = 0.406; E(f(x)) = 0.00
Iter: 112; Median = 0.405; E(f(x)) = 0.00
Iter: 113; Median = 0.405; E(f(x)) = 0.00
Iter: 114; Median = 0.406; E(f(x)) = 0.00
Iter: 115; Median = 0.406; E(f(x)) = 0.00
Iter: 116; Median = 0.406; E(f(x)) = 0.00
Iter: 117; Median = 0.406; E(f(x)) = 0.00
Iter: 118; Median = 0.406; E(f(x)) = 0.00
Iter: 119; Median = 0.406; E(f(x)) = 0.00
Iter: 120; Median = 0.405; E(f(x)) = 0.00
Iter: 121; Median = 0.406; E(f(x)) = 0.00
Iter: 122; Median = 0.405; E(f(x)) = 0.00
Iter: 123; Median = 0.406; E(f(x)) = 0.00
Iter: 124; Median = 0.405; E(f(x)) = 0.00
Iter: 125; Median = 0.406; E(f(x)) = 0.00
Iter: 126; Median = 0.405; E(f(x)) = 0.00
Iter: 127; Median = 0.405; E(f(x)) = 0.00
Iter: 128; Median = 0.405; E(f(x)) = 0.00
Iter: 129; Median = 0.405; E(f(x)) = 0.00
Iter: 130; Median = 0.405; E(f(x)) = 0.00
Iter: 131; Median = 0.406; E(f(x)) = 0.00
Iter: 132; Median = 0.406; E(f(x)) = 0.00
Iter: 133; Median = 0.406; E(f(x)) = 0.00
Iter: 134; Median = 0.406; E(f(x)) = 0.00
Iter: 135; Median = 0.405; E(f(x)) = 0.00
Iter: 136; Median = 0.405; E(f(x)) = 0.00
Iter: 137; Median = 0.406; E(f(x)) = 0.00
Iter: 138; Median = 0.406; E(f(x)) = 0.00
Iter: 139; Median = 0.405; E(f(x)) = 0.00
Iter: 140; Median = 0.405; E(f(x)) = 0.00
Iter: 141; Median = 0.405; E(f(x)) = 0.00
Iter: 142; Median = 0.405; E(f(x)) = 0.00
Iter: 143; Median = 0.405; E(f(x)) = 0.00
Iter: 144; Median = 0.406; E(f(x)) = 0.00
Iter: 145; Median = 0.405; E(f(x)) = 0.00
Iter: 146; Median = 0.405; E(f(x)) = 0.00
Iter: 147; Median = 0.406; E(f(x)) = 0.00
Iter: 148; Median = 0.405; E(f(x)) = 0.00
Iter: 149; Median = 0.406; E(f(x)) = 0.00
Iter: 150; Median = 0.406; E(f(x)) = 0.00
Iter: 151; Median = 0.405; E(f(x)) = 0.00
Iter: 152; Median = 0.405; E(f(x)) = 0.00
Iter: 153; Median = 0.406; E(f(x)) = 0.00
Iter: 154; Median = 0.405; E(f(x)) = 0.00
Iter: 155; Median = 0.406; E(f(x)) = 0.00
Iter: 156; Median = 0.405; E(f(x)) = 0.00
Iter: 157; Median = 0.405; E(f(x)) = 0.00
Iter: 158; Median = 0.405; E(f(x)) = 0.00
Iter: 159; Median = 0.405; E(f(x)) = 0.00
Iter: 160; Median = 0.405; E(f(x)) = 0.00
Iter: 161; Median = 0.406; E(f(x)) = 0.00
Iter: 162; Median = 0.405; E(f(x)) = 0.00
Iter: 163; Median = 0.406; E(f(x)) = 0.00
Iter: 164; Median = 0.405; E(f(x)) = 0.00
Iter: 165; Median = 0.405; E(f(x)) = 0.00
Iter: 166; Median = 0.406; E(f(x)) = 0.00
Iter: 167; Median = 0.406; E(f(x)) = 0.00
Iter: 168; Median = 0.405; E(f(x)) = 0.00
Iter: 169; Median = 0.405; E(f(x)) = 0.00
Iter: 170; Median = 0.406; E(f(x)) = 0.00
Iter: 171; Median = 0.406; E(f(x)) = 0.00
retpba
#> $root
#> [1] 0.4055406
#> 
#> $terminated_early
#> [1] TRUE
#> 
#> $time
#> [1] 0.12s
#> 
#> $iterations
#> [1] 172
#> 
retpba$root
#> [1] 0.4055406
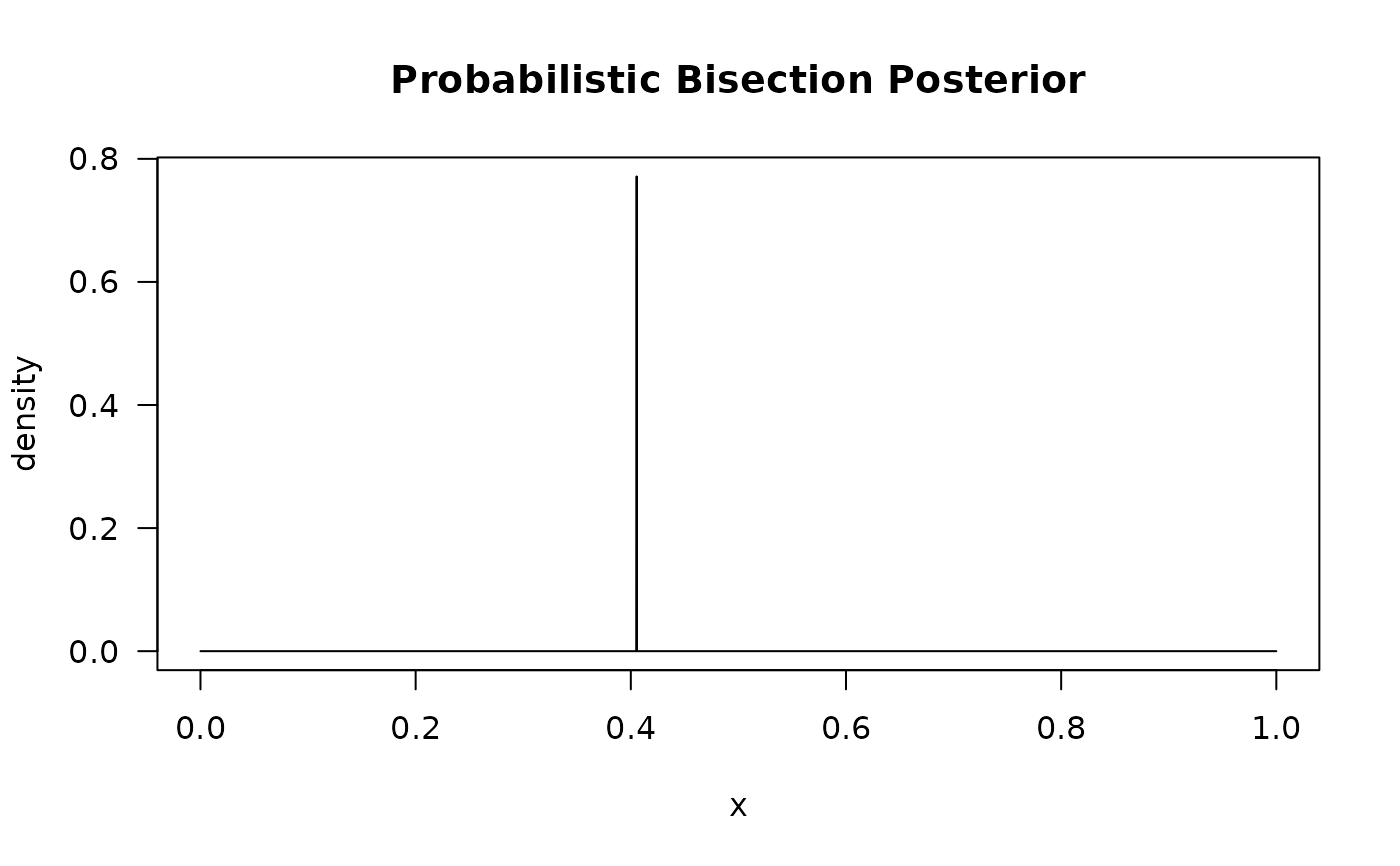
plot(retpba)

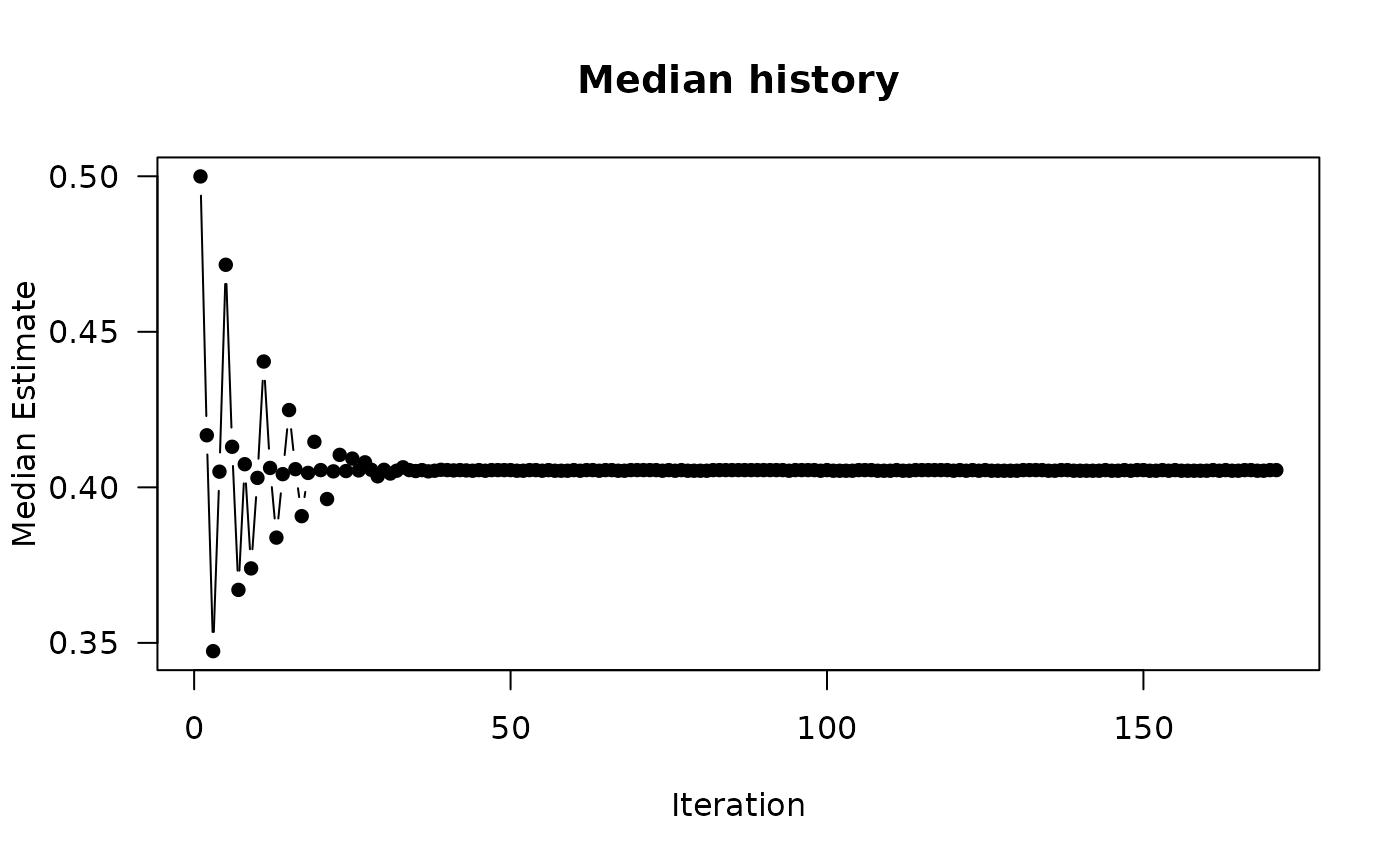
plot(retpba, type = 'history')


# Same problem, however root function is now noisy. Hence, need to solve
#  fhat(x) - b + e = 0, where E(e) = 0
f.root_noisy <- function(x) 1 / (1 + exp(-x)) - .6 + rnorm(1, sd=.02)
sapply(rep(.3, 10), f.root_noisy)
#>  [1] -0.039123616 -0.001791425 -0.023427438 -0.028433850 -0.066480674
#>  [6] -0.006044210 -0.018417790 -0.017867592 -0.033764287 -0.023880012

# uniroot "converges" unreliably
set.seed(123)
uniroot(f.root_noisy, c(0,1))$root
#> [1] 0.3748233
uniroot(f.root_noisy, c(0,1))$root
#> [1] 0.3785736
uniroot(f.root_noisy, c(0,1))$root
#> [1] 0.4954932

# probabilistic bisection provides better convergence
retpba.noise <- PBA(f.root_noisy, c(0,1))
#> 
Iter: 1; Median = 0.500; E(f(x)) = 0.02
Iter: 2; Median = 0.417; E(f(x)) = 0.02
Iter: 3; Median = 0.347; E(f(x)) = 0.00
Iter: 4; Median = 0.405; E(f(x)) = 0.00
Iter: 5; Median = 0.472; E(f(x)) = 0.00
Iter: 6; Median = 0.413; E(f(x)) = 0.00
Iter: 7; Median = 0.462; E(f(x)) = 0.01
Iter: 8; Median = 0.420; E(f(x)) = 0.00
Iter: 9; Median = 0.455; E(f(x)) = 0.00
Iter: 10; Median = 0.426; E(f(x)) = 0.01
Iter: 11; Median = 0.388; E(f(x)) = 0.00
Iter: 12; Median = 0.421; E(f(x)) = 0.00
Iter: 13; Median = 0.396; E(f(x)) = 0.01
Iter: 14; Median = 0.352; E(f(x)) = 0.00
Iter: 15; Median = 0.390; E(f(x)) = 0.00
Iter: 16; Median = 0.415; E(f(x)) = 0.00
Iter: 17; Median = 0.394; E(f(x)) = 0.01
Iter: 18; Median = 0.366; E(f(x)) = 0.01
Iter: 19; Median = 0.392; E(f(x)) = 0.00
Iter: 20; Median = 0.409; E(f(x)) = 0.00
Iter: 21; Median = 0.424; E(f(x)) = 0.00
Iter: 22; Median = 0.412; E(f(x)) = 0.00
Iter: 23; Median = 0.396; E(f(x)) = 0.00
Iter: 24; Median = 0.380; E(f(x)) = 0.00
Iter: 25; Median = 0.356; E(f(x)) = 0.00
Iter: 26; Median = 0.377; E(f(x)) = 0.00
Iter: 27; Median = 0.360; E(f(x)) = 0.00
Iter: 28; Median = 0.374; E(f(x)) = 0.00
Iter: 29; Median = 0.363; E(f(x)) = 0.00
Iter: 30; Median = 0.373; E(f(x)) = 0.00
Iter: 31; Median = 0.388; E(f(x)) = 0.00
Iter: 32; Median = 0.398; E(f(x)) = 0.00
Iter: 33; Median = 0.391; E(f(x)) = 0.00
Iter: 34; Median = 0.396; E(f(x)) = 0.00
Iter: 35; Median = 0.409; E(f(x)) = 0.00
Iter: 36; Median = 0.417; E(f(x)) = 0.00
Iter: 37; Median = 0.410; E(f(x)) = 0.00
Iter: 38; Median = 0.400; E(f(x)) = 0.00
Iter: 39; Median = 0.393; E(f(x)) = 0.00
Iter: 40; Median = 0.398; E(f(x)) = 0.00
Iter: 41; Median = 0.408; E(f(x)) = 0.00
Iter: 42; Median = 0.399; E(f(x)) = 0.00
Iter: 43; Median = 0.394; E(f(x)) = 0.00
Iter: 44; Median = 0.398; E(f(x)) = 0.00
Iter: 45; Median = 0.406; E(f(x)) = 0.00
Iter: 46; Median = 0.399; E(f(x)) = 0.00
Iter: 47; Median = 0.405; E(f(x)) = 0.00
Iter: 48; Median = 0.410; E(f(x)) = 0.00
Iter: 49; Median = 0.406; E(f(x)) = 0.00
Iter: 50; Median = 0.400; E(f(x)) = 0.00
Iter: 51; Median = 0.405; E(f(x)) = 0.00
Iter: 52; Median = 0.401; E(f(x)) = 0.00
Iter: 53; Median = 0.398; E(f(x)) = 0.00
Iter: 54; Median = 0.401; E(f(x)) = 0.00
Iter: 55; Median = 0.398; E(f(x)) = 0.00
Iter: 56; Median = 0.400; E(f(x)) = 0.00
Iter: 57; Median = 0.403; E(f(x)) = 0.00
Iter: 58; Median = 0.400; E(f(x)) = 0.00
Iter: 59; Median = 0.399; E(f(x)) = 0.00
Iter: 60; Median = 0.396; E(f(x)) = 0.00
Iter: 61; Median = 0.399; E(f(x)) = 0.00
Iter: 62; Median = 0.397; E(f(x)) = 0.00
Iter: 63; Median = 0.394; E(f(x)) = 0.00
Iter: 64; Median = 0.391; E(f(x)) = 0.00
Iter: 65; Median = 0.394; E(f(x)) = 0.00
Iter: 66; Median = 0.392; E(f(x)) = 0.00
Iter: 67; Median = 0.393; E(f(x)) = 0.00
Iter: 68; Median = 0.395; E(f(x)) = 0.00
Iter: 69; Median = 0.394; E(f(x)) = 0.00
Iter: 70; Median = 0.395; E(f(x)) = 0.00
Iter: 71; Median = 0.394; E(f(x)) = 0.00
Iter: 72; Median = 0.393; E(f(x)) = 0.00
Iter: 73; Median = 0.394; E(f(x)) = 0.00
Iter: 74; Median = 0.394; E(f(x)) = 0.00
Iter: 75; Median = 0.396; E(f(x)) = 0.00
Iter: 76; Median = 0.398; E(f(x)) = 0.00
Iter: 77; Median = 0.396; E(f(x)) = 0.00
Iter: 78; Median = 0.398; E(f(x)) = 0.00
Iter: 79; Median = 0.397; E(f(x)) = 0.00
Iter: 80; Median = 0.395; E(f(x)) = 0.00
Iter: 81; Median = 0.397; E(f(x)) = 0.00
Iter: 82; Median = 0.398; E(f(x)) = 0.00
Iter: 83; Median = 0.397; E(f(x)) = 0.00
Iter: 84; Median = 0.395; E(f(x)) = 0.00
Iter: 85; Median = 0.397; E(f(x)) = 0.00
Iter: 86; Median = 0.398; E(f(x)) = 0.00
Iter: 87; Median = 0.398; E(f(x)) = 0.00
Iter: 88; Median = 0.399; E(f(x)) = 0.00
Iter: 89; Median = 0.398; E(f(x)) = 0.00
Iter: 90; Median = 0.398; E(f(x)) = 0.00
Iter: 91; Median = 0.397; E(f(x)) = 0.00
Iter: 92; Median = 0.396; E(f(x)) = 0.00
Iter: 93; Median = 0.397; E(f(x)) = 0.00
Iter: 94; Median = 0.398; E(f(x)) = 0.00
Iter: 95; Median = 0.398; E(f(x)) = 0.00
Iter: 96; Median = 0.398; E(f(x)) = 0.00
Iter: 97; Median = 0.397; E(f(x)) = 0.00
Iter: 98; Median = 0.397; E(f(x)) = 0.00
Iter: 99; Median = 0.398; E(f(x)) = 0.00
Iter: 100; Median = 0.398; E(f(x)) = 0.00
Iter: 101; Median = 0.398; E(f(x)) = 0.00
Iter: 102; Median = 0.400; E(f(x)) = 0.00
Iter: 103; Median = 0.399; E(f(x)) = 0.00
Iter: 104; Median = 0.398; E(f(x)) = 0.00
Iter: 105; Median = 0.399; E(f(x)) = 0.00
Iter: 106; Median = 0.398; E(f(x)) = 0.00
Iter: 107; Median = 0.398; E(f(x)) = 0.00
Iter: 108; Median = 0.398; E(f(x)) = 0.00
Iter: 109; Median = 0.398; E(f(x)) = 0.00
Iter: 110; Median = 0.398; E(f(x)) = 0.00
Iter: 111; Median = 0.398; E(f(x)) = 0.00
Iter: 112; Median = 0.398; E(f(x)) = 0.00
Iter: 113; Median = 0.398; E(f(x)) = 0.00
Iter: 114; Median = 0.398; E(f(x)) = 0.00
Iter: 115; Median = 0.398; E(f(x)) = 0.00
Iter: 116; Median = 0.398; E(f(x)) = 0.00
Iter: 117; Median = 0.398; E(f(x)) = 0.00
Iter: 118; Median = 0.398; E(f(x)) = 0.00
Iter: 119; Median = 0.398; E(f(x)) = 0.00
Iter: 120; Median = 0.398; E(f(x)) = 0.00
Iter: 121; Median = 0.398; E(f(x)) = 0.00
Iter: 122; Median = 0.398; E(f(x)) = 0.00
Iter: 123; Median = 0.398; E(f(x)) = 0.00
Iter: 124; Median = 0.398; E(f(x)) = 0.00
Iter: 125; Median = 0.398; E(f(x)) = 0.00
Iter: 126; Median = 0.398; E(f(x)) = 0.00
Iter: 127; Median = 0.398; E(f(x)) = 0.00
Iter: 128; Median = 0.398; E(f(x)) = 0.00
Iter: 129; Median = 0.398; E(f(x)) = 0.00
Iter: 130; Median = 0.398; E(f(x)) = 0.00
Iter: 131; Median = 0.398; E(f(x)) = 0.00
Iter: 132; Median = 0.398; E(f(x)) = 0.00
Iter: 133; Median = 0.398; E(f(x)) = 0.00
Iter: 134; Median = 0.399; E(f(x)) = 0.00
Iter: 135; Median = 0.399; E(f(x)) = 0.00
Iter: 136; Median = 0.398; E(f(x)) = 0.00
Iter: 137; Median = 0.398; E(f(x)) = 0.00
retpba.noise
#> $root
#> [1] 0.3984398
#> 
#> $terminated_early
#> [1] TRUE
#> 
#> $time
#> [1] 0.09s
#> 
#> $iterations
#> [1] 138
#> 
plot(retpba.noise)

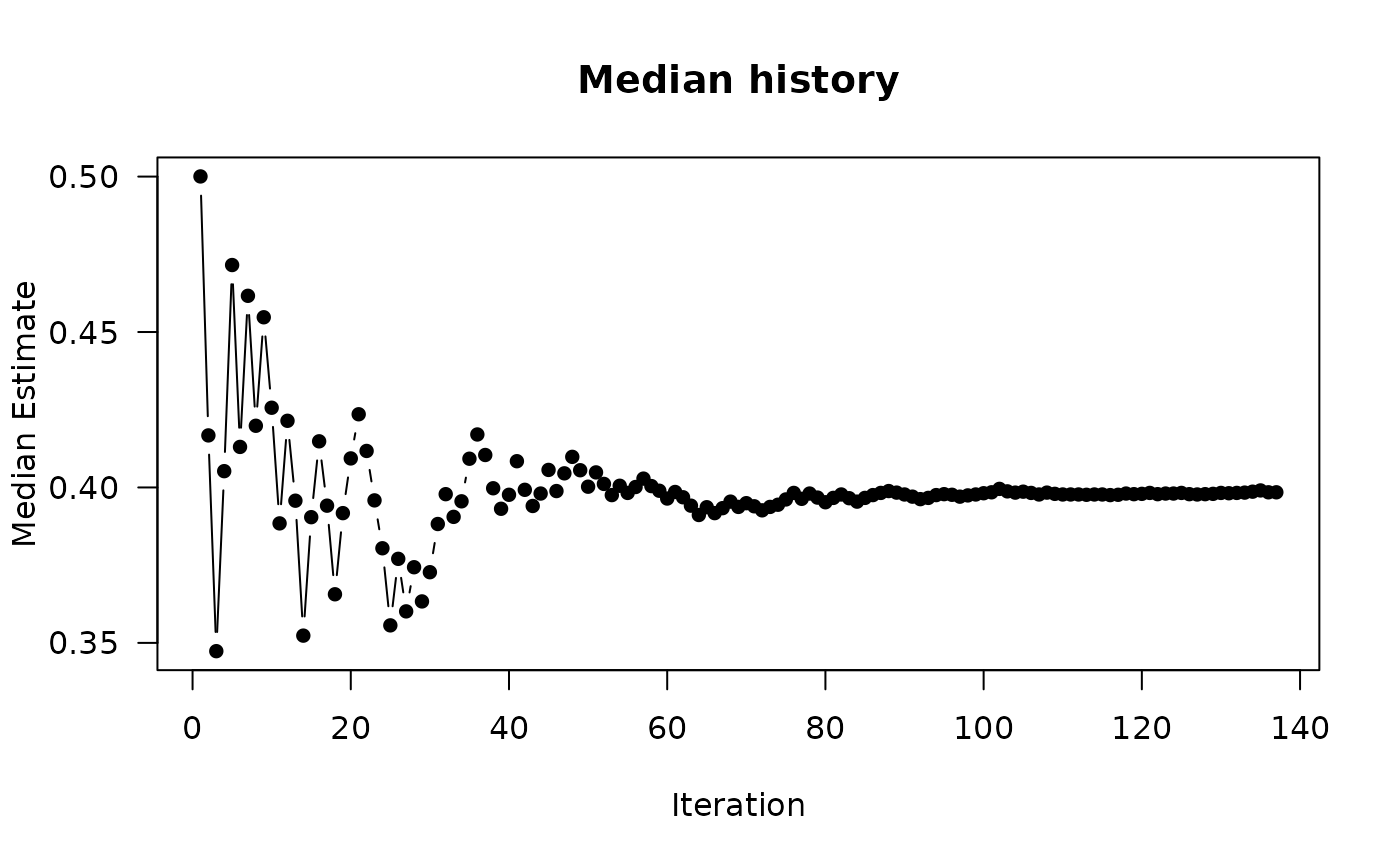
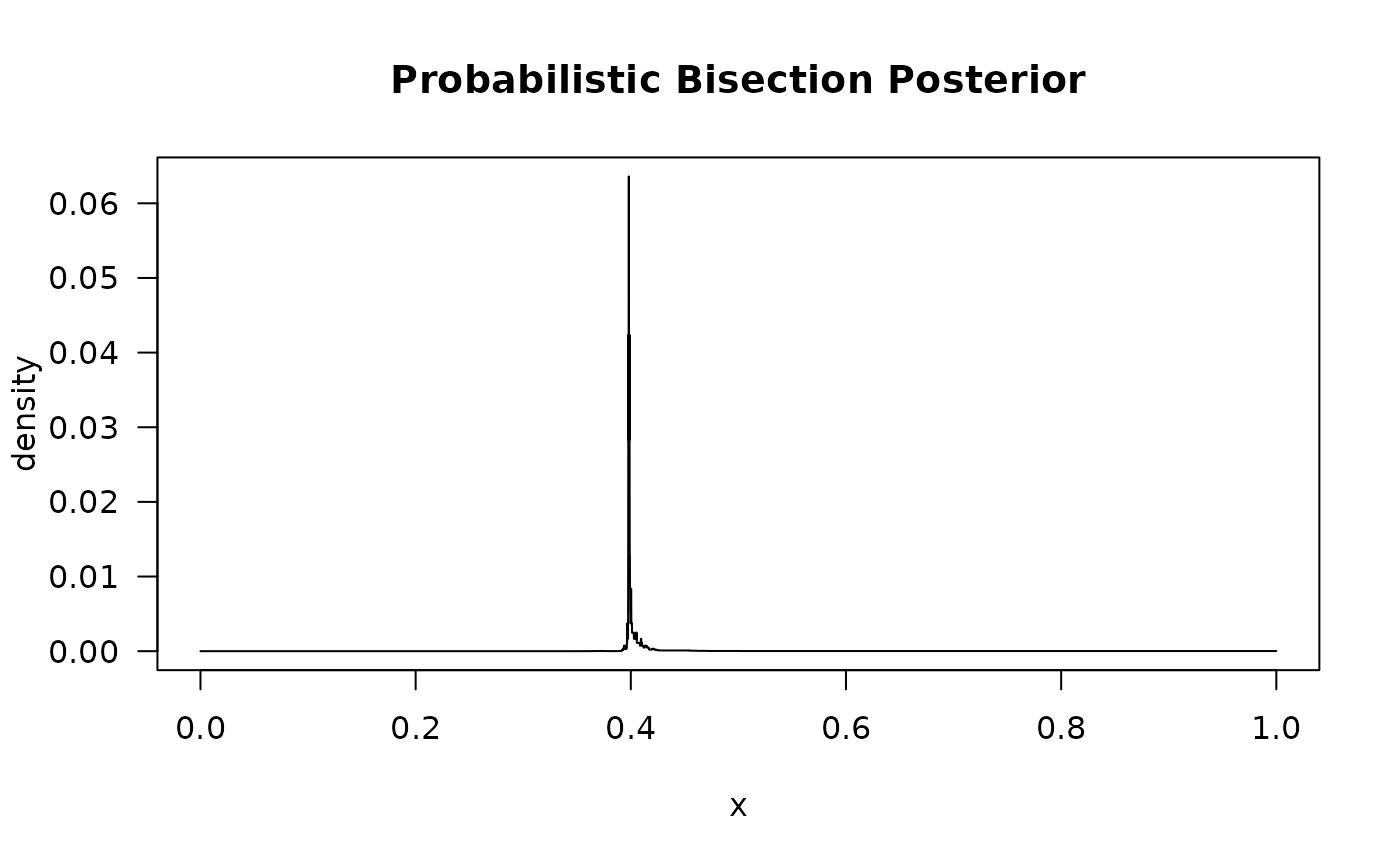plot(retpba.noise, type = 'history')


if (FALSE) { # \dontrun{
# ignore termination criteria and instead run for 30 seconds or 30000 iterations
retpba.noise_30sec <- PBA(f.root_noisy, c(0,1), wait.time = "0:30", maxiter=30000)
retpba.noise_30sec

} # }