Generate data with the multivariate t distribution

Function generates data from the multivariate t distribution given a covariance matrix, non-centrality parameter (or mode), and degrees of freedom.

rmvt(n, sigma, df, delta = rep(0, nrow(sigma)), Kshirsagar = FALSE)

Arguments

n: number of observations to generate
sigma: positive definite covariance matrix
df: degrees of freedom. df = 0 and df = Inf corresponds to the multivariate normal distribution
delta: the vector of non-centrality parameters of length n which specifies the either the modes (default) or non-centrality parameters
Kshirsagar: logical; triggers whether to generate data with non-centrality parameters or to adjust the simulated data to the mode of the distribution. The default uses the mode

Value

a numeric matrix with columns equal to ncol(sigma)

References

Chalmers, R. P., & Adkins, M. C. (2020). Writing Effective and Reliable Monte Carlo Simulations with the SimDesign Package. The Quantitative Methods for Psychology, 16(4), 248-280. doi:10.20982/tqmp.16.4.p248

Sigal, M. J., & Chalmers, R. P. (2016). Play it again: Teaching statistics with Monte Carlo simulation. Journal of Statistics Education, 24(3), 136-156. doi:10.1080/10691898.2016.1246953

Author

Phil Chalmers rphilip.chalmers@gmail.com

Examples


# random t values given variances [3,6], covariance 2, and df = 15
sigma <- matrix(c(3,2,2,6), 2, 2)
x <- rmvt(1000, sigma = sigma, df = 15)
head(x)
#>            [,1]       [,2]
#> [1,]  1.3042822 -2.0318613
#> [2,]  0.4853400 -0.9843646
#> [3,] -0.4545143 -2.8552338
#> [4,] -2.1102930 -1.9951739
#> [5,]  0.4620754 -0.8522892
#> [6,] -1.1569847 -5.6485164
summary(x)
#>        V1                 V2          
#>  Min.   :-6.21426   Min.   :-10.4157  
#>  1st Qu.:-1.23958   1st Qu.: -1.8521  
#>  Median :-0.06359   Median : -0.1496  
#>  Mean   :-0.05056   Mean   : -0.0373  
#>  3rd Qu.: 1.23545   3rd Qu.:  1.8817  
#>  Max.   : 6.65206   Max.   : 10.8285  
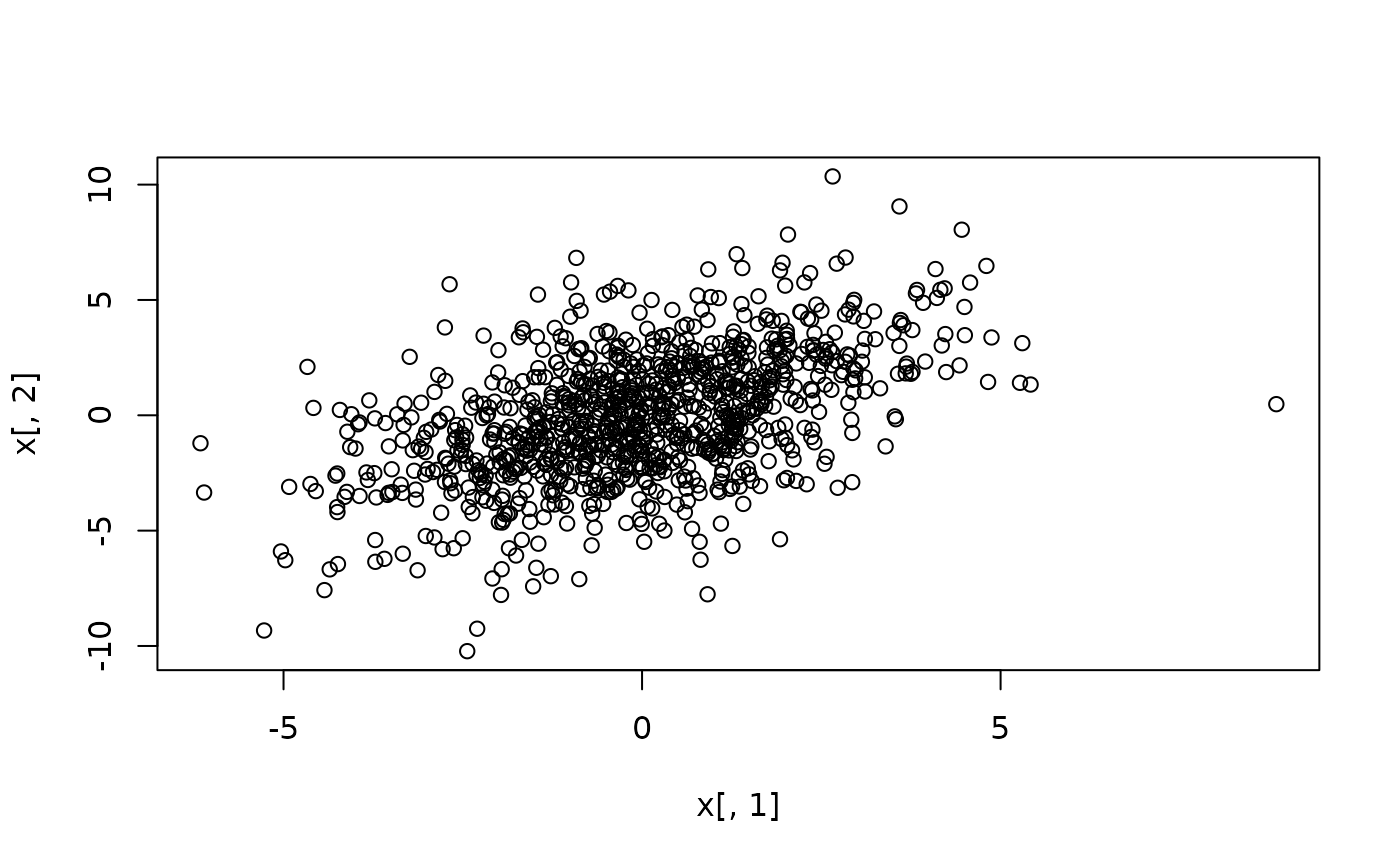
plot(x[,1], x[,2])