Introduction to the Spower package

This vignette provides a brief introduction to using the package Spower for prospective/post-hoc, a priori, sensitivity, criterion, and compromise power analyses. For a more detailed description of the package structure and philosophy please refer to associated publication (Chalmers, 2025), as well as the documentation found within the functions; particularly, Spower(), SpowerBatch(), and SpowerCurve().

Types of functions

There are generally two ways to go about using Spower. The first is by utilizing one of a handful of build-in simulation experiments with an associated data-generation and analysis, or more flexibility (but less user friendly) by constructing a user-defined simulation experiment by way of writing simulation code that is encapsulated inside a single function. In either case, the goal is to design R code to perform a given simulation experiment with a set of meaningful (often scalar) functional arguments, where the output from this function returns either:

A suitable $p$ -value under the null hypothesis statistical testing (NHST) paradigm, $P(D|H_0)$ ,
The posterior probability of a (typically alternative) hypothesis, $P(H_1|D)$ , or
A logical value indicating support for the hypothesis of interest

For the first two cases, the $p$ value returned is compared to a suitable cut-off defined by the package (e.g., is $p$ less than $\alpha=.05$ for the first option, while the second might be $p$ greater than $\alpha.95$ ), and therefore converted to a TRUE/FALSE value internally, while the ladder does not require such a transformation. In all cases, the average of the resulting TRUE/FALSE values reflects something to do with statistical power (e.g., TRUE if rejecting the null; TRUE if supporting the alternative; some more complicated combination involving precision, multiple hypotheses, regions of practical equivalence/significance, etc), thereby forming the basis for all subsequent power analysis procedures.

The internal functions available in Spower primarily focuses on the first approach criteria involving NHST $p$ -values, as this is historically the most common in similar software (e.g., GPower 3), however nothing precludes Spower from more complex and interesting power analyses. See the vignette “Logical Vectors, Bayesian power analyses and ROPEs” for more advanced examples involving confidence intervals (CIs), parameter precision criterion, regions of practical equivalences (ROPEs), equivalence tests, Bayes Factors, and power analyses involving posterior probabilities. See also the vignette “Type S and Type M errors” for conditional power evaluation information to estimate sign (S) and magnitude (M) power information and their respective Type S and Type M errors (Gelman and Carlin, 2014).

Built-in simulation experiments

Spower ships with several common statistical inference experiments, such as those involving linear regression models, mediation analyses, ANOVAs, $t$ -tests, correlations, and so on. The simulation experiments are organized with the prefix p_, followed by the name of the analysis method. For instance,

p_lm.R2(50, k=3, R2=.3)

## [1] 0.004935905

performs a single simulation experiment reflecting the null hypothesis $H_0:\, R^2=0$ for a linear regression model with $k=3$ predictor variables and a sample size of $N=50$ .

Translating this information into a power analysis context now simply requires passing this experiment to Spower() (the details of which are discussed below), where by default the estimate of power ( $1-\hat{\beta}$ ) is returned using the default sig.level = .05.

p_lm.R2(50, k=3, R2=.3) |> Spower()

## 
## Execution time (H:M:S): 00:00:41
## Design conditions: 
## 
## # A tibble: 1 × 5
##       n    R2     k sig.level power
##   <dbl> <dbl> <dbl>     <dbl> <lgl>
## 1    50   0.3     3      0.05 NA   
## 
## Estimate of power: 0.971
## 95% Confidence Interval: [0.968, 0.974]

Each of the p_* functions return a $p$ -value ( $P(D|H_0$ ) as this is the general information required to evaluate statistical power with Spower(). Alternatively, users may define their own simulation functions if the desired experiment has not been defined within the package.

User-defined simulation experiments

As a very simple example, suppose one were interested in the power to reject the null hypothesis $H_0:\, \mu = \mu_0$ in a one-sample $t$ -test scenario, where $P(D|H_0)$ is the probability of the data given the null hypothesis of interest. Note that while the package already supports this type of analysis (see help(p_t.test)) it is instructive to see how users they can write their own version of this experiment, as this will help in defining simulations outside what is currently included in the package.

p_single.t <- function(n, mean, mu=0){
    g <- rnorm(n, mean=mean)
    p <- t.test(g, mu=mu)$p.value
    p
}

This simulation experiment will first obtain sample of data drawn from a Gaussian distribution with some specific mean ( $\mu$ ), and evaluate the conditional probability that the data were generated from a population with a $\mu_0=0$ (the null; hence, $P(D|\mu_0=0)$ ). As such, the $p$ -value returned from this experiments reflects the probability of observing the data given the null hypothesis $H_0:\, \mu=\mu_0$ , or more specifically $H_0:\, \mu=0$ , for a single generated dataset.

# a single experiment
p_single.t(n=100, mean=.2)

## [1] 0.06328707

From here, a suitable cut-off is required to evaluate whether the experiment was ‘significant’, which is the purpose of the parameter $\alpha$ . Specifically, if the observed data ( $D$ ) were plausibly drawn from a population with $\mu_0$ (hence, $P(D|\mu_0) \ge \alpha$ ) then a FALSE significance would be returned; otherwise, if the data were unlikely to have been observed given the ( $P(D|\mu_0=0) < \alpha$ ) then a TRUE would be returned, thereby indicating statistical significance.

For convenience, and for the purpose of other types of specialized power analyses (e.g., compromise analyses), the $\alpha$ parameter has been controlled via the argument Spower(..., sig.level = .05), which creates the TRUE/FALSE evaluations internally. This saves a step in the writing, but if users wished to defined sig.level within the simulation experiment itself that is an acceptable approach too.

Types of power analyses to evaluate

For power analyses there are typically four parameters that can be manipulated/solved in a given experiment: the $\alpha$ level (Type I error, often reflexively set to $\alpha=.05$ ), power (the complement of the Type II error, $1-\beta$ ), an effect size of interest, and the sample size. Given three of these values, the fourth can always be solved.

Note that the above description reflects a general rule-of-thumb, as there may be multiple effect sizes of interest, multiple sample size definitions (e.g., in the form of cluster sizes in multi-level models), and so on. Regardless, in Spower() switching between these types of power analysis criteria is performed simply by explicitly specifying which parameter is missing (NA), as demonstrated below, and therefore specific naming conventions for the type of analysis being performed is not particularly important, though the following presentation may be instructive nonetheless.

Prospective/post-hoc power analysis

The canonical setup for Spower() will evaluate prospective or post-hoc power, thereby obtaining the estimate $1-\hat{\beta}$ . By default, Spower() uses $10,000$ independent simulation replications to estimate the power when this is the target criterion.

Given the above simulation definition, the following provides an estimate of power given the null hypothesis $H_0:\, \mu=0.3$ given that the data were generated from a distribution with $\mu = .5$ with $n=100$ .

p_single.t(n=100, mean=.5, mu=.3) |> Spower() -> prospective
prospective

## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 5
##       n  mean    mu sig.level power
##   <dbl> <dbl> <dbl>     <dbl> <lgl>
## 1   100   0.5   0.3      0.05 NA   
## 
## Estimate of power: 0.515
## 95% Confidence Interval: [0.505, 0.525]

Compromise power analysis

Compromise power analysis involves manipulating the $\alpha$ level until some sufficient balance between the Type I and Type II error rates are met, expressed in terms of the ratio $q=\frac{\beta}{\alpha}$ .

In Spower, there are two ways to approach this criterion. The first, which focuses on the beta_alpha ratio at the outset, requires passing the target ratio to Spower() using the same setup as the previous prospective power analysis.

p_single.t(n=100, mean=.5, mu=.3) |> 
    Spower(beta_alpha=4) -> compromise
compromise

## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 6
##       n  mean    mu sig.level power beta_alpha
##   <dbl> <dbl> <dbl>     <dbl> <lgl>      <dbl>
## 1   100   0.5   0.3        NA NA             4
## 
## Estimate of Type I error rate (alpha/sig.level): 0.093
## 95% Confidence Interval: [0.087, 0.098]
## 
## Estimate of power (1-beta): 0.629
## 95% Confidence Interval: [0.620, 0.638]

This returns the estimated sig.level ( $\hat{\alpha}$ ) and resulting $\hat{\beta}$ that satisfies the target $q$ ratio $q = \beta/\alpha = 4$ .

# satisfies q = 4 ratio
with(compromise, (1 - power) / sig.level)

## [1] 4

The second way to perform a compromise analysis is to re-use a previous evaluation of a prospective/post-hoc power analysis, as this contains all the necessary information for obtaining the compromise estimates.

# using previous post-hoc/prospective power analysis
update(prospective, beta_alpha=4)

## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 6
##       n  mean    mu sig.level power beta_alpha
##   <dbl> <dbl> <dbl>     <dbl> <lgl>      <dbl>
## 1   100   0.5   0.3        NA NA             4
## 
## Estimate of Type I error rate (alpha/sig.level): 0.093
## 95% Confidence Interval: [0.088, 0.099]
## 
## Estimate of power (1-beta): 0.627
## 95% Confidence Interval: [0.617, 0.636]

In either case, the use of S3 generic update() function can be beneficial as the stored result may be reused with alternative beta_alpha values, thereby avoiding the need to estimate new experimental data.

A priori power analysis

The goal of a priori power analysis is generally to obtain the sample size ( $N$ ) associated with a specific power rate of interest (e.g., $1-\beta=.90$ ), which is useful in the context of future data collection planning.

To estimate the sample size using Monte Carlo simulation experiments, Spower() performs stochastic root solving using the ProBABLI approach from the SimDesign package (see SimSolve()), and therefore requires a specific search interval to search within. The width of the interval should reflect a plausible range where the researcher believes the solution to lie, however this may be quite large as well as ProBABLI is less influenced by the range of the search interval (Chalmers, 2024). Moreover, as the algorithm is fundamentally based on bisections, the midpoint of the specified interval should be organized to reflect the researcher’s “best guess” of where the solution is likely to be, though this is generally only worth considering if the simulation experiment under evaluation is very time consuming.

Below the sample size n is solved to achieve a target power of $1-\beta=.80$ , where the solution for $N$ was suspected to lie somewhere between the search interval = c(20, 200), with the initial starting guess of $\hat{N}=(20 + 200)/2=110$ (quite far from the true solution, but in this case adds little to the overall computation time).

p_single.t(n=NA, mean=.5) |> 
    Spower(power=.8, interval=c(20,200))

## 
## Execution time (H:M:S): 00:00:25
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    NA   0.5      0.05   0.8
## 
## Estimate of n: 32.8
## 95% Predicted Confidence Interval: [32.4, 33.1]

Equivalently, rather than placing the interval definition within Spower() and providing a suitable NA placeholder to indicate which argument interval pertains to, the function interval() can be used directly in the experiment definition argument. Hence, the following will be identical to the above example, though requires less back-and-forth reading between the pipe seperator.

p_single.t(n=interval(20, 200), mean=.5) |> Spower(power=.8)

## 
## Execution time (H:M:S): 00:00:25
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    NA   0.5      0.05   0.8
## 
## Estimate of n: 32.8
## 95% Predicted Confidence Interval: [32.4, 33.1]

Of course, the output will still be presented in terms of the NA placeholder logic, however in this case the user does not need to specify the NA explicitly as it is clear from context.

Sensitivity power analysis

Similar to a priori power analysis, in that stochastic root solving is required, the target of sensitivity analysis is to locate some specific standardized or unstandardized effect size that will result in a particular power rate. This pertains to the question of how large an effect size must be in order to reliably detect the effect of interest, holding constant other information such as sample size.

Below the sample size is fixed at $N=100$ , while the interval for the standardized effect size $d$ is searched between c(.1, 3). Note that the use of decimals in the interval tells Spower() to use a continuous rather than discrete search space (cf. with a priori, which uses an integer search space for the simulation replicates).

p_single.t(n=100, mean=NA) |> 
    Spower(power=.8, interval=c(.1, 3))

## 
## Execution time (H:M:S): 00:00:20
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1   100    NA      0.05   0.8
## 
## Estimate of mean: 0.281
## 95% Predicted Confidence Interval: [0.280, 0.283]

Equivalently, using interval() (not run).

# p_single.t(n=100, mean=interval(.1, 3)) |> Spower(power=.8)

Criterion power analysis

Finally, in criterion power analysis the goal is to locate the associated $\alpha$ level (sig.level) required to achieve a target power output holding constant the other modeling information. This is done in Spower() by setting the sig.level input to NA while providing values for the other parameters. Note that technically no search interval is require in this context as $\alpha$ necessarily lies between the interval $[0,1]$ .

p_single.t(n=50, mean=.5) |> 
    Spower(power=.8, sig.level=NA)

## 
## Execution time (H:M:S): 00:00:18
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    50   0.5        NA   0.8
## 
## Estimate of sig.level: 0.010
## 95% Predicted Confidence Interval: [0.009, 0.010]

Multiple power evaluation functions

The following functions, SpowerBatch() and SpowerCurve(), can be used to evaluate and visualize power analysis results across a range of inputs rather than a single set of fixed inputs. This section demonstrates their general usage, as their specifications slightly differ from that of Spower(), despite the fact that Spower() is the underlying estimation engine.

SpowerBatch()

To begin, suppose that there were interest in evaluating the p_single.t() function across multiple $n$ inputs to obtain estimates of $1-\beta$ . While this could be performed using independent calls to Spower(), the function SpowerBatch() can be used instead, where the variable inputs can be specified in a suitable vector format.

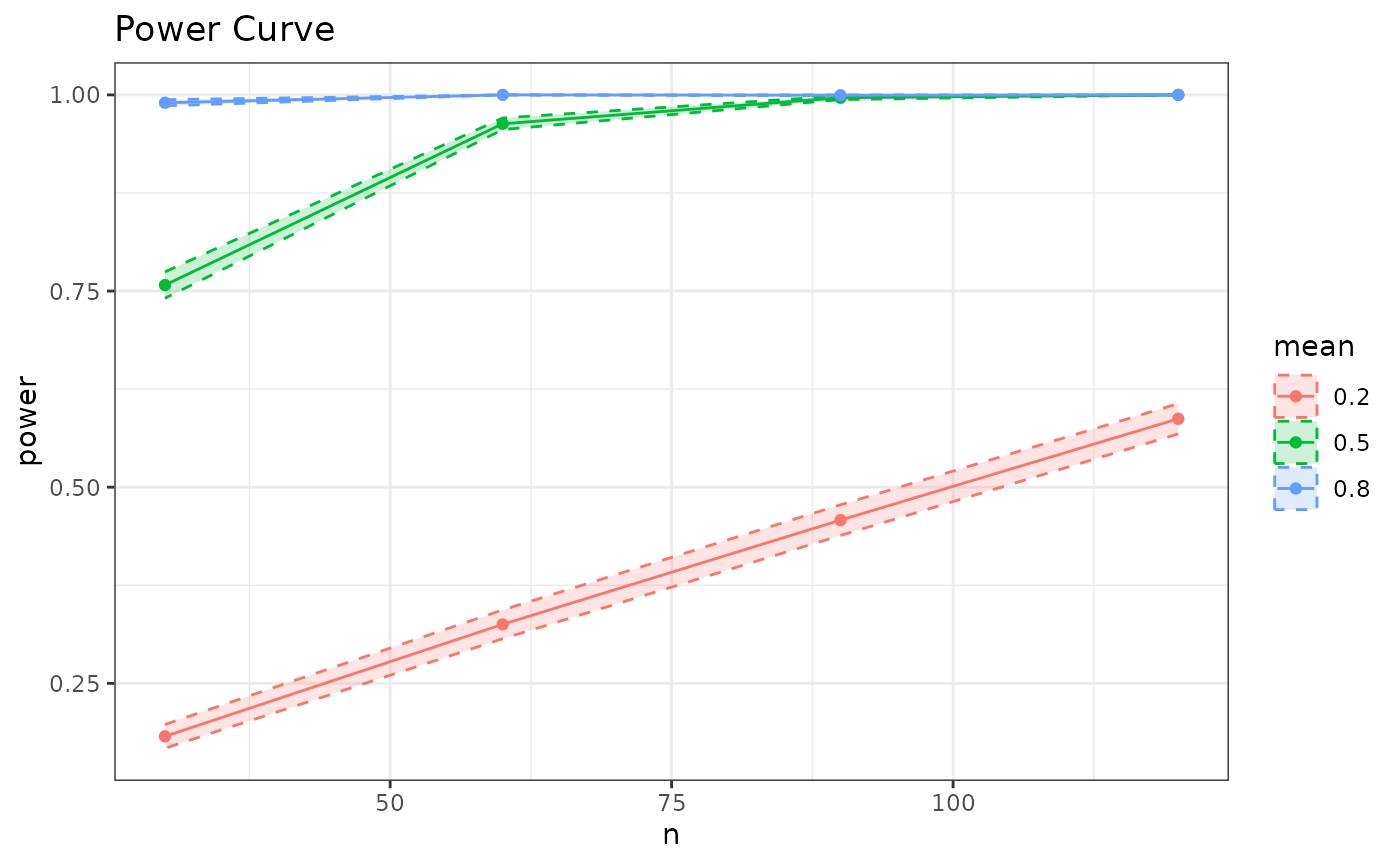
For instance, given the effect size $\mu=.5$ , what would the power be to reject the null hypothesis $H_0:\, \mu=0$ across three different sample sizes, $N = [30,60,90]$ ?

p_single.t(mean=.5) |> 
    SpowerBatch(n=c(30, 60, 90)) -> prospective.batch
prospective.batch

## $CONDITION_1
## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <lgl>
## 1    30   0.5      0.05 NA   
## 
## Estimate of power: 0.752
## 95% Confidence Interval: [0.743, 0.760]
## 
## $CONDITION_2
## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <lgl>
## 1    60   0.5      0.05 NA   
## 
## Estimate of power: 0.967
## 95% Confidence Interval: [0.963, 0.970]
## 
## $CONDITION_3
## 
## Execution time (H:M:S): 00:00:03
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <lgl>
## 1    90   0.5      0.05 NA   
## 
## Estimate of power: 0.996
## 95% Confidence Interval: [0.995, 0.997]

This can further be coerced to a data.frame object if there is reason to do so (e.g., for plotting purposes, though see also SpowerCurve()).

as.data.frame(prospective.batch)

##    n mean sig.level  power    CI_2.5   CI_97.5
## 1 30  0.5      0.05 0.7516 0.7431313 0.7600687
## 2 60  0.5      0.05 0.9669 0.9633937 0.9704063
## 3 90  0.5      0.05 0.9963 0.9951100 0.9974900

Similarly, if the were related to a priori analyses for sample size planning then the inputs to SpowerBatch() would be modified to set n to the missing quantity.

apriori.batch <- p_single.t(mean=.5, n=NA) |> 
    SpowerBatch(power=c(.7, .8, .9), interval=c(20, 200)) 
apriori.batch

## $CONDITION_1
## 
## Execution time (H:M:S): 00:00:41
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    NA   0.5      0.05   0.7
## 
## Estimate of n: 26.7
## 95% Predicted Confidence Interval: [26.5, 27.0]
## 
## $CONDITION_2
## 
## Execution time (H:M:S): 00:00:21
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    NA   0.5      0.05   0.8
## 
## Estimate of n: 33.3
## 95% Predicted Confidence Interval: [32.9, 33.7]
## 
## $CONDITION_3
## 
## Execution time (H:M:S): 00:00:33
## Design conditions: 
## 
## # A tibble: 1 × 4
##       n  mean sig.level power
##   <dbl> <dbl>     <dbl> <dbl>
## 1    NA   0.5      0.05   0.9
## 
## Estimate of n: 44.4
## 95% Predicted Confidence Interval: [43.8, 44.8]

as.data.frame(apriori.batch)

##          n mean sig.level power   CI_2.5  CI_97.5
## 1 26.71726  0.5      0.05   0.7 26.46683 26.96011
## 2 33.31082  0.5      0.05   0.8 32.90640 33.69844
## 3 44.36998  0.5      0.05   0.9 43.76155 44.84176

SpowerCurve()

Often times researchers wish to visualize the results of power analyses in the form of graphical representations. Spower supports various types of visualizations through the function SpowerCurve(), which creates power curve plots of previously obtained results (e.g., via SpowerBatch()) or for to-be-explored inputs. Importantly, each graphic contains estimates of the Monte Carlo sampling uncertainty to deter over-interpretation of any resulting point-estimates.

To demonstrate, suppose one were interested in visualizing the power for the running single-sample $t$ test across four different sample sizes, $N=[30,60,90,120]$ . To do this requires passing the simulation experiment and varying information to the function SpowerCurve(), which fills in the variable information to the supplied simulation experiment and plots the resulting output.

p_single.t(mean=.5) |> 
    SpowerCurve(n=c(30, 60, 90, 120))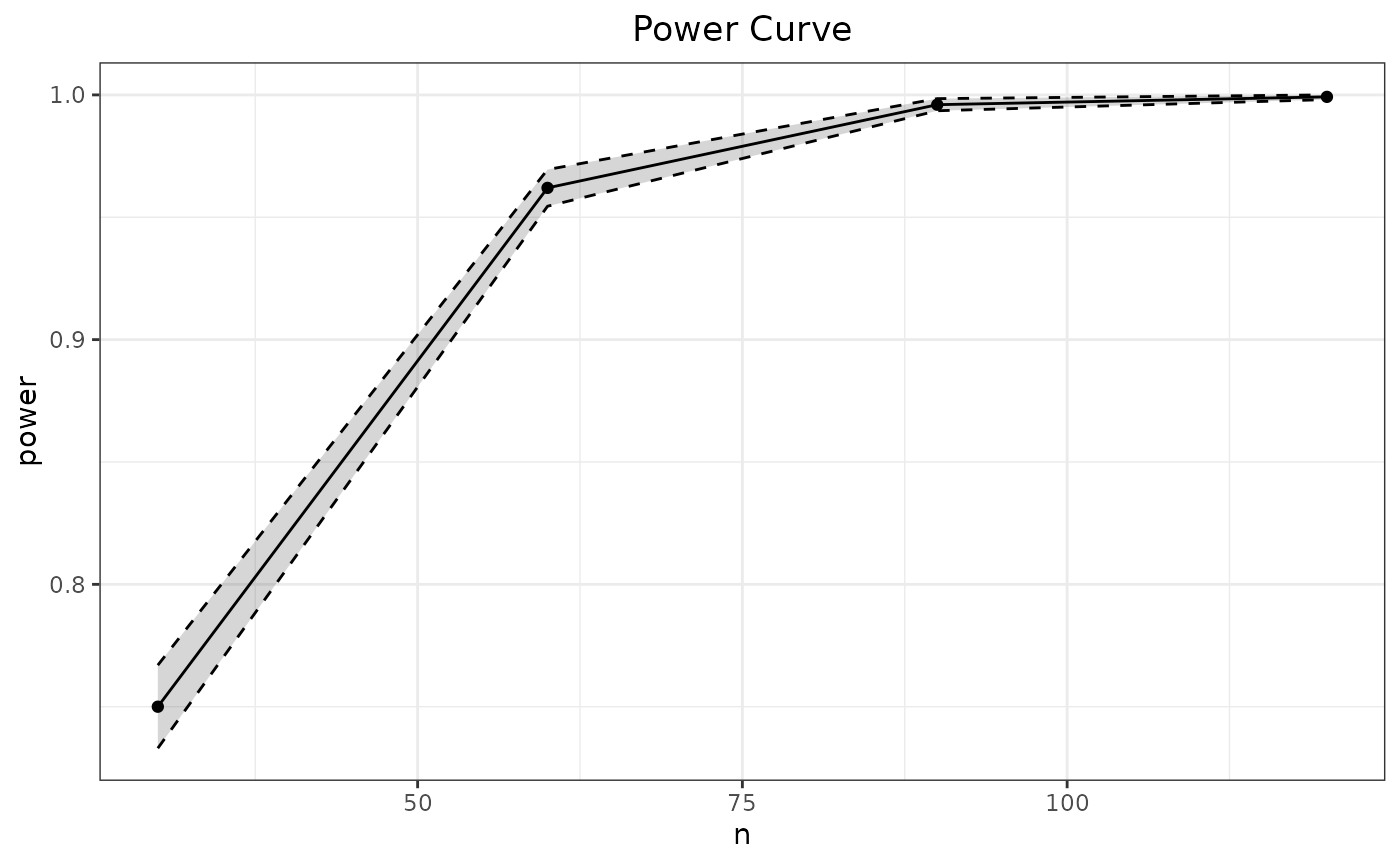

Alternatively, were the above information already evaluated using SpowerBatch() then this batch object could be passed directly to SpowerCurve()’s argument batch, thereby avoiding the need to re-evaluate the simulation experiments.

# pass previous SpowerBatch() object
SpowerCurve(batch=batch)

SpowerCurve() will accept as many arguments as exists in the supplied simulation experiment definition, however it will only provide aesthetic mappings for the first three variable input specifications as anything past this becomes more difficult to display automatically. Below is an example that varies both the n input as well as the input mean, where the first input appears on the $x$ -axis while the second is mapped to the default colour aesthetic in ggplot2.

p_single.t() |> 
    SpowerCurve(n=c(30, 60, 90, 120), mean=c(.2, .5, .8))

Phil Chalmers

February 13, 2026